一种新型张拉整体并联机构刚度及动力学分析

doi:10.13229/j.cnki.jdxbgxb20170879

摘要/Abstract

摘要：

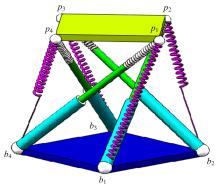
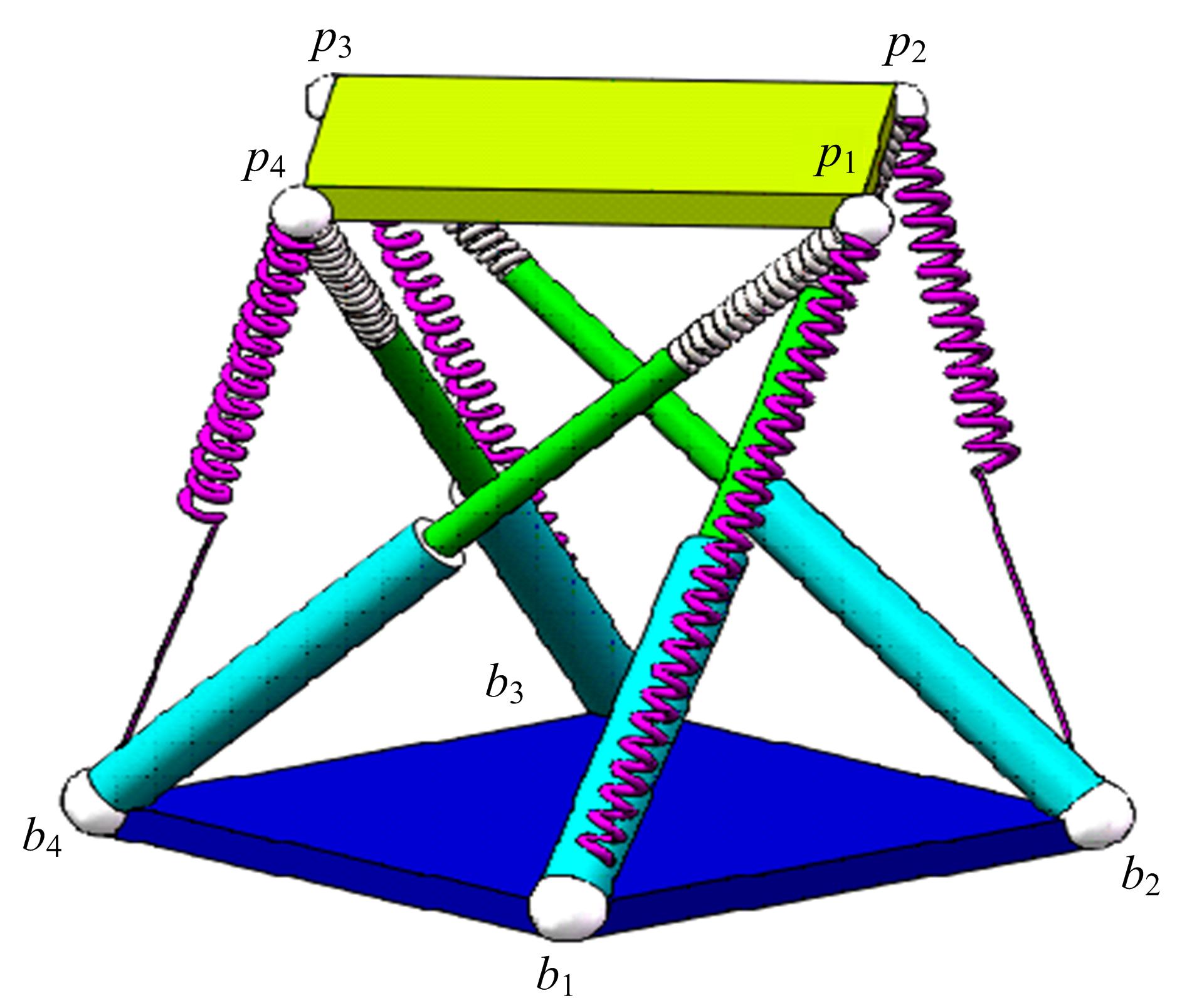
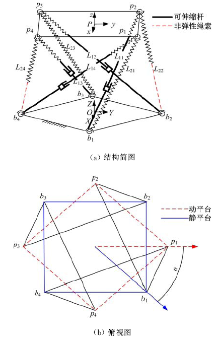
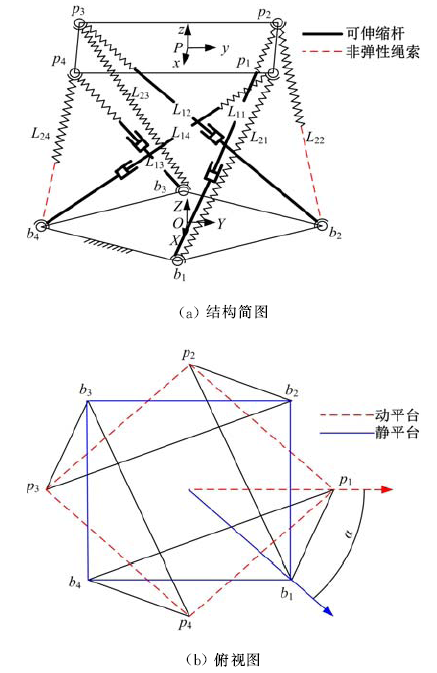
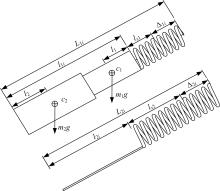
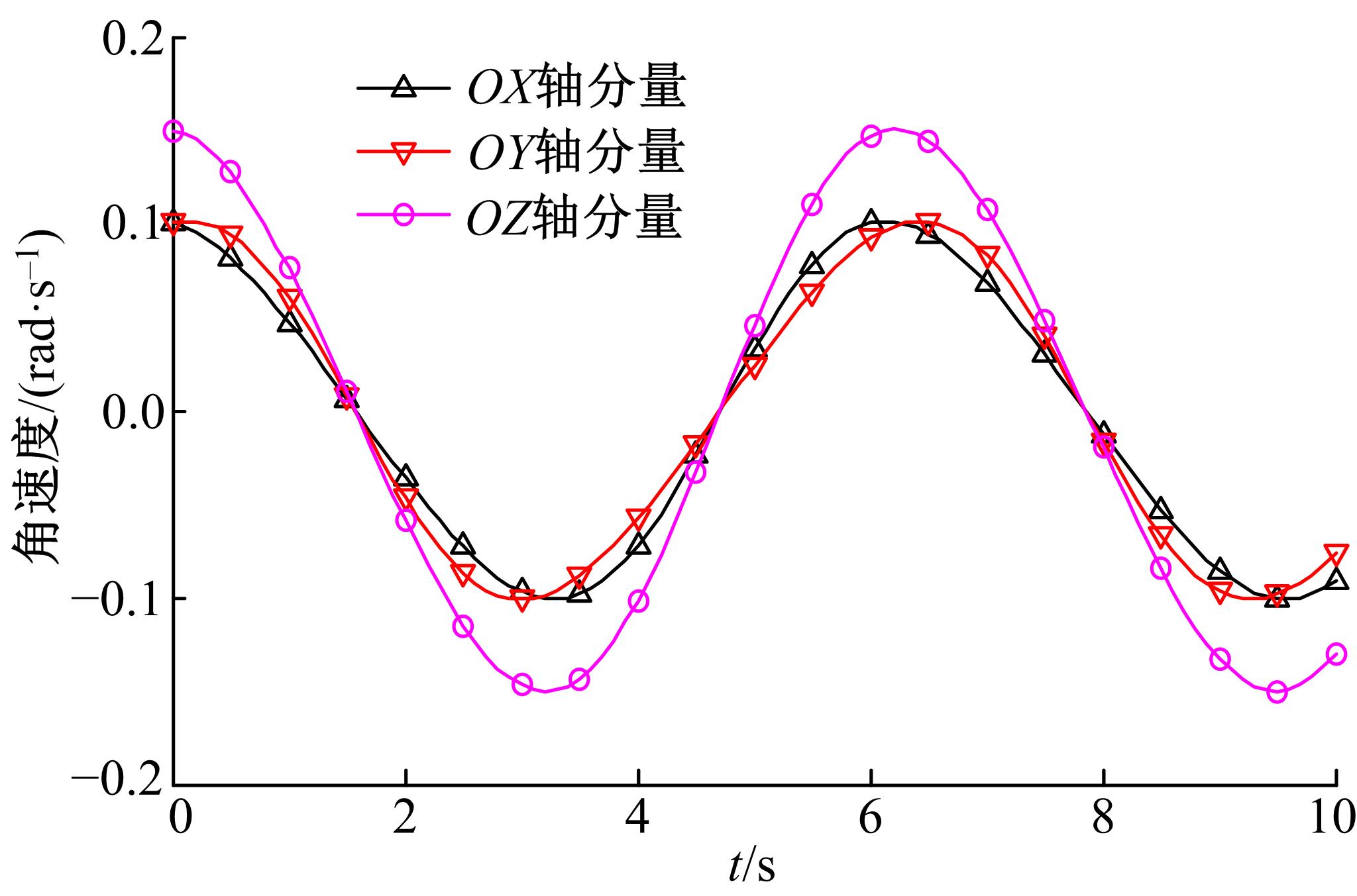
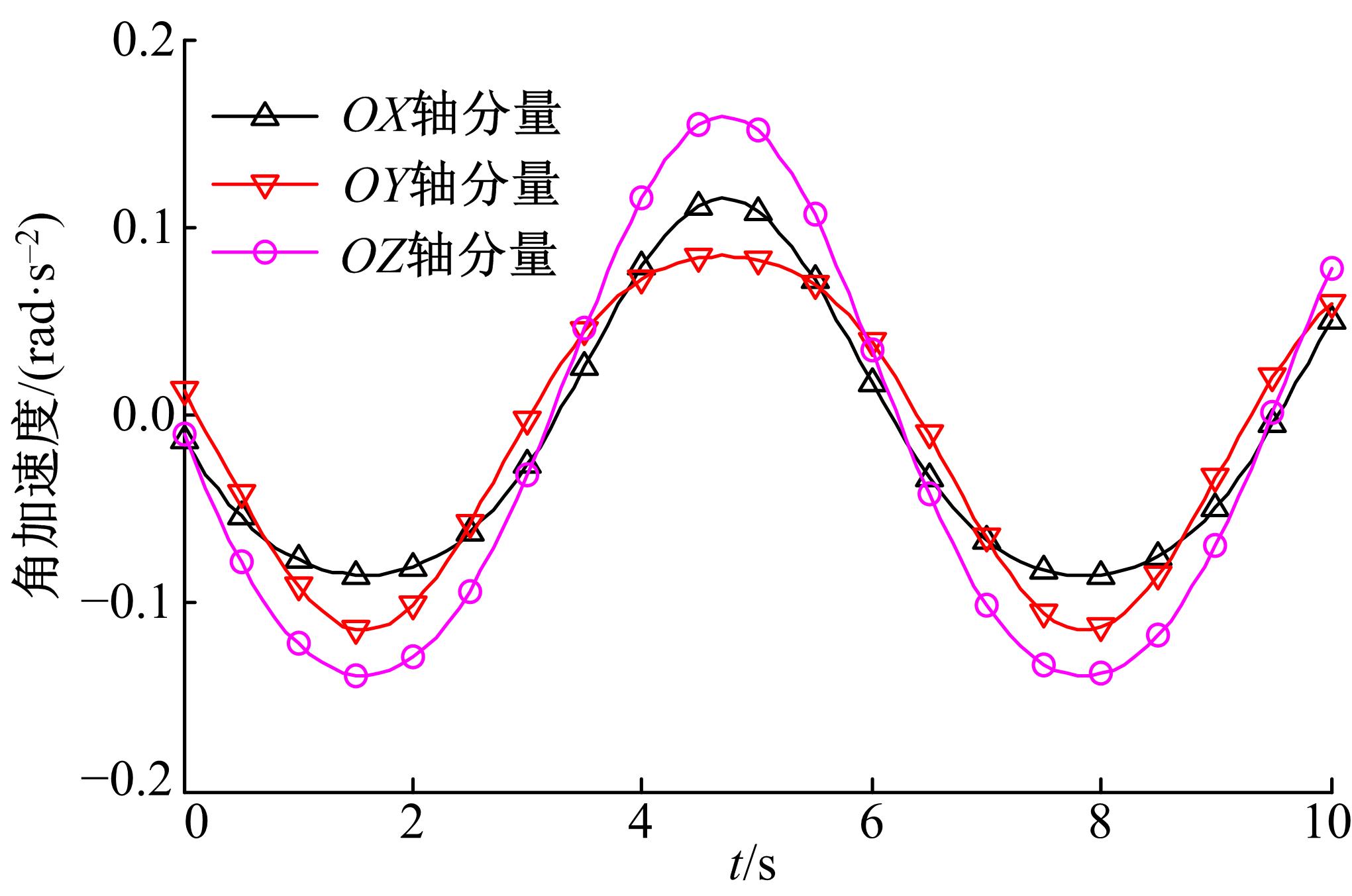
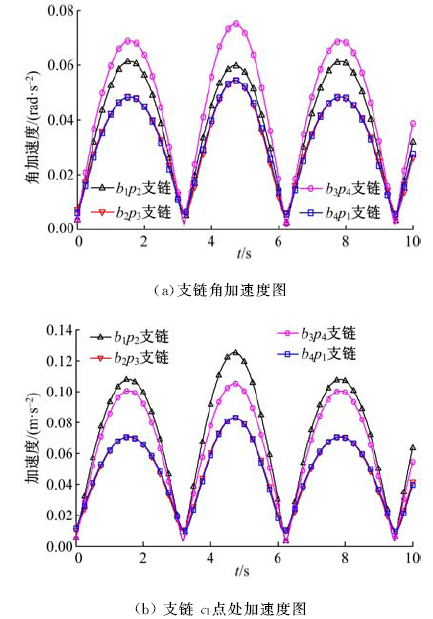
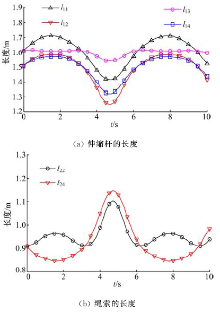
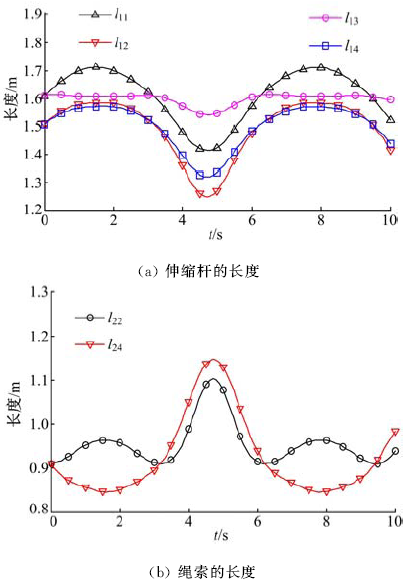
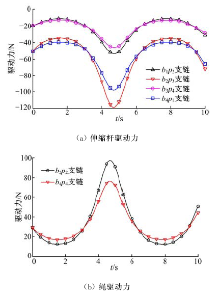
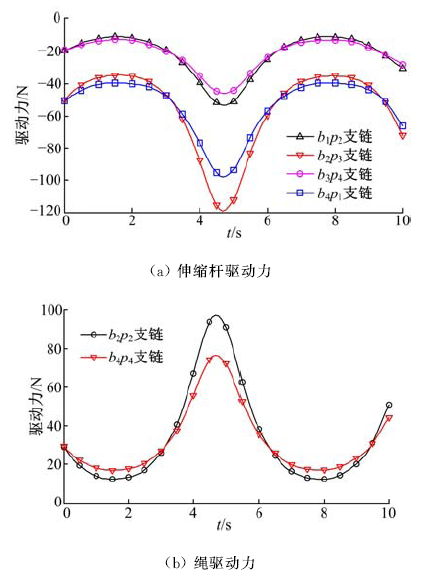
为了提高精密机械手的操作柔顺性,提出了一种四棱柱型六自由度张拉整体并联机构模型,由4条刚性驱动支链、2条绳索驱动支链和2条弹簧支链组成。建立了机构的运动学模型,推导了机构动平台角速度、角加速度与欧拉角之间的转化关系;根据螺旋理论建立了机构的静态平衡方程,从而进一步推导出机构的刚度矩阵表达式,并得到矩阵数值解;运用虚功原理建立了机构的伪刚体动力学方程。最后,对机构的速度、加速度、动力学方程进行数值计算、仿真,验证了上述数学模型的正确性,为该机构动力学特性的深入分析和控制策略的研究提供了理论参考。

关键词: 机械设计及理论, 张拉整体, 并联机构, 静态分析, 刚度矩阵, 动力学

Abstract:

The tensegrity mechanism is a new type of rigid-flexible spatial model, with advantages of light weight, easy-folded, extended flexibility and high precision. In order to improve the compliance of precise manipulators during normal operation, a model for tensegrity parallel mechanism in six DOF was proposed, which was built in quadrilateral prism type. The proposed model was mainly composed of four rigid drive branched chains, two rope drive links and two branched springs. The kinematics equation of the mechanism was established by closed vector method, and the relation between the angular velocity, the angular acceleration and the Euler angle during platform moving was deduced. According to the screw theory, the static equilibrium equation and the stiffness matrix of the mechanism were derived to solve out the numerical values. After that, the pseudo-rigid-body dynamics pattern of the mechanism was set up by the principle of virtual work. Finally, the velocity, acceleration and dynamic equations of the mechanism were numerically calculated. Based on the calculated values, simulations were conducted in MATLAB to verify the above mathematical solutions. This research provides theoretical references for the further studies on dynamics characteristics and control strategies of this mechanism.

Key words: mechanical design and theory, tensegrity, parallel mechanism, static analysis, stiffness matrix, dynamics

中图分类号:

TH112

朱伟,王传伟,顾开荣,沈惠平,许可,汪源. 一种新型张拉整体并联机构刚度及动力学分析[J]. 吉林大学学报(工学版), 2018, 48(6): 1777-1786.

ZHU Wei,WANG Chuan-wei,GU Kai-rong,SHEN Hui-ping,XU Ke,WANG Yuan. Stiffness and dynamics analysis of a new type of tensegrity parallel mechanism[J]. Journal of Jilin University(Engineering and Technology Edition), 2018, 48(6): 1777-1786.

图/表 9

图1

图2

图3

表1

机构参数"

参数	数值	参数	数值
p/m	0.5	$l s 2$ /m	0.6
b/m	0.75	l₁/m	0.3
m/kg	2	l₂/m	0.3
m₁/kg	0.4	k₁/(N·m^-1)	300
m₂/kg	0.5	k₂/(N·m^-1)	200
$l s 1$ /m	0.3

表1

图4

图5

图6

图7

图8

参考文献 21

[1]	Snelson K D . Continuous tension, discontinuous compression structures[P]. US 3169611, 1965.
[2]	Fuller R B . Tensile-integrity structures[P]. US 3063521, 1962.
[3]	李团结, 车明奎 . 张拉整体结构外力与形变间关系分析及实验验证[J]. 西安电子科技大学学报, 2017,44(1):24-28.
	Li Tuan-jie, Che Ming-kui . Analysis and experimental verification of relationship between external force and deformation of tensegrity structures[J]. Jouranal of Xidian University, 2017,44(1):24-28.
[4]	罗阿妮, 王龙昆, 刘贺平 . 张拉整体三棱柱构型和结构稳定性分析[J]. 哈尔滨工业大学学报, 2016,48(7):82-87. doi: 10.11918/j.issn.0367-6234.2016.07.013
	Luo A-ni, Wang Long-kun, Liu He-ping . Analysis of configuration and structural stability of 3-bar tensegrity prism[J]. Journal of Harbin Institute of Technolocy, 2016,48(7):82-87. doi: 10.11918/j.issn.0367-6234.2016.07.013
[5]	Oppenheim I, Williams W . Tensegrity prisms as adaptive structures[J]. ASME Int'l Mechanical Engineering Congress, 1997,54(8):113-120.
[6]	Arsenault M . Determination of the analytical workspace boundaries of a novel 2-DoF planar tensegrity mechanism[J]. Transactions of the Canadian Society for Mechanical Engineering, 2010,34(1):75-91. doi: 10.1139/tcsme-2010-0005
[7]	Arsenault M, Gosselin C M . Kinematic, static and dynamic analysis of a planar 2-DoF tensegrity mechanism[J]. Mechanism & Machine Theory, 2005,41(9):1072-1089.
[8]	Marshall M Q . Analysis of tensegrity-based parallelplatform devices[D]. Gainesville: Department of Mechanical and Aerospace Engineering, University of Florida, 2003.
[9]	Arsenault M, Gosselin C M . Kinematic and static Analysis of 3-PUPS spatial tensegrity mechanism[J]. Mechanism & Machine Theory, 2009,44(1):162-179. doi: 10.1016/j.mechmachtheory.2008.02.005
[10]	Shekarforoush S M M, Eghtesad M, Farid M. Design of statically balanced six-degree-of-freedom parallel mechanisms based on tensegrity system [C]//ASME 2009 International Mechanical Engineering Congress and Exposition, Lake Buena Vista, Florida,USA, 2009: 245-253.
[11]	Abadi B N R, Farid M, Mahzoon M . Introducing and analyzing a novel three-degree-of-freedom spatial tensegrity mechanism[J]. Journal of Computational & Nonlinear Dynamics, 2014,9(2):94-94.
[12]	Moon Y , Crane Ⅲ C D,Roberts R G. Reserve kinetostatic analysis and stiffness of a spatial tensegrity-based compliant mechanism[J]. Mechanism and Machine Theory, 2013,70(6):320-337. doi: 10.1016/j.mechmachtheory.2013.05.001
[13]	纪志飞 . 3-SPS张拉整体并联机构的构型综合与运动性能分析及能量采集研究[D]. 西安:西安电子科技大学机电工程学院, 2014.
	Ji Zhi-fei . On type synthesis, kinematic performances and energy harvesting of 3-SPS tensegrity parallel mechanisms[D]. Xi'an:School of Mechano-electronic Engineering,Xidian University, 2014.
[14]	Chen S, Arsenault M. Workspace computation and analysis of a planar 2-DoF translational tensegrity mechanism [C]//ASME 2010 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Montreal, Quebec, Canada, 2010: 223-232.
[15]	Arsenault M, Gosselin C M . Kinematic and static analysis of a three-degree-of-freedom spatial modular tensegrity mechanism.[J]. International Journal of Robotics Research, 2008,27(8):951-966. doi: 10.1177/0278364908091152
[16]	Ji Zhe-fei, Li Tuan-jie, Lin Min . Kinematics, singularity, and workspaces of a planar 4-Bar tensegrity mechanism[J]. Journal of Robotics, 2014,2014(11):1-10.
[17]	Ji Zhe-fei, Li Tuan-jie, Lin Min . Kinematic and static analysis of a planar compliant tensegrity-like parallel mechanism[J]. Australian Journal of Mechanical Engineering, 2014,12(1):49-59. doi: 10.7158/M12-077.2014.12.1
[18]	Ji Zhe-fei, Li Tuan-jie, Lin Min . Kinematics, workspaces and stiffness of a planar class-2 tensegrity mechanism[J]. UPB Sci Bull, 2014,76(3):53-64.
[19]	王征 . 张拉整体结构的找形和稳定性分析[D]. 西安:西安电子科技大学机电工程学院, 2012.
	Wang Zheng . Analysis of form-finding and stability of tensegrity structures[D]. Xi'an:School of Mechano-electronic Engineering, Xidian University, 2012.
[20]	Wittenburg J . Dynamics of Multibody Systems[M]. New York: Springer, 2008: 80-96.
[21]	Ball R S. A Treatise on the Theory of Screws[M]. New York: Cambridge University Press, 1900: 120-160.

相关文章 15

[1]	贾拓,赵丁选,崔玉鑫. 铰接式装载机倾翻预警方法[J]. 吉林大学学报(工学版), 2018, 48(6): 1762-1769.
[2]	李战东,陶建国,罗阳,孙浩,丁亮,邓宗全. 核电水池推力附着机器人系统设计[J]. 吉林大学学报(工学版), 2018, 48(6): 1820-1826.
[3]	刘兆惠, 王超, 吕文红, 管欣. 基于非线性动力学分析的车辆运行状态参数数据特征辨识[J]. 吉林大学学报(工学版), 2018, 48(5): 1405-1410.
[4]	毛宇泽, 王黎钦. 鼠笼支撑一体化结构对薄壁球轴承承载性能的影响[J]. 吉林大学学报(工学版), 2018, 48(5): 1508-1514.
[5]	胡满江, 罗禹贡, 陈龙, 李克强. 基于纵向频响特性的整车质量估计[J]. 吉林大学学报(工学版), 2018, 48(4): 977-983.
[6]	刘祥勇, 李万莉. 包含蓄能器的电液比例控制模型[J]. 吉林大学学报(工学版), 2018, 48(4): 1072-1084.
[7]	张琳, 章新杰, 郭孔辉, 王超, 刘洋, 刘涛. 未知环境下智能汽车轨迹规划滚动窗口优化[J]. 吉林大学学报(工学版), 2018, 48(3): 652-660.
[8]	王靖宇, 于旭涛, 胡兴军, 郭鹏, 辛俐, 郭峰, 张扬辉. 汽车外后视镜流致振特性及其流动机理[J]. 吉林大学学报(工学版), 2017, 47(6): 1669-1676.
[9]	李静, 张家旭, 张艳华, 陈立军. 采用强跟踪中心差分滤波器的汽车状态和参数估计[J]. 吉林大学学报(工学版), 2017, 47(5): 1329-1335.
[10]	许金凯, 王煜天, 张世忠. 驱动冗余重型并联机构的动力学性能[J]. 吉林大学学报(工学版), 2017, 47(4): 1138-1143.
[11]	王倩, 赵丁选, 赵颖, 陈娜. 舰载直升机复杂舰面上的动力学分析[J]. 吉林大学学报(工学版), 2017, 47(4): 1109-1113.
[12]	李显生, 孟祥雨, 郑雪莲, 程竹青, 任圆圆. 非满载罐体内液体冲击动力学特性[J]. 吉林大学学报(工学版), 2017, 47(3): 737-743.
[13]	张义花, 许洪国, 刘宏飞, 王发继. 双挂汽车列车高速阶跃横向失稳能量分析[J]. 吉林大学学报(工学版), 2017, 47(1): 71-75.
[14]	李玲, 施树明, 王宪彬, 于壮. 发动机制动下高速转弯车辆稳定性[J]. 吉林大学学报(工学版), 2017, 47(1): 64-70.
[15]	罗乐, 郑旭, 吕义, 郝志勇. 高速列车车轮及轮对的声辐射特性[J]. 吉林大学学报(工学版), 2016, 46(5): 1464-1470.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed