基于压缩感知理论的宽带信号波达方向估计

doi:10.13229/j.cnki.jdxbgxb20200694

摘要/Abstract

摘要：

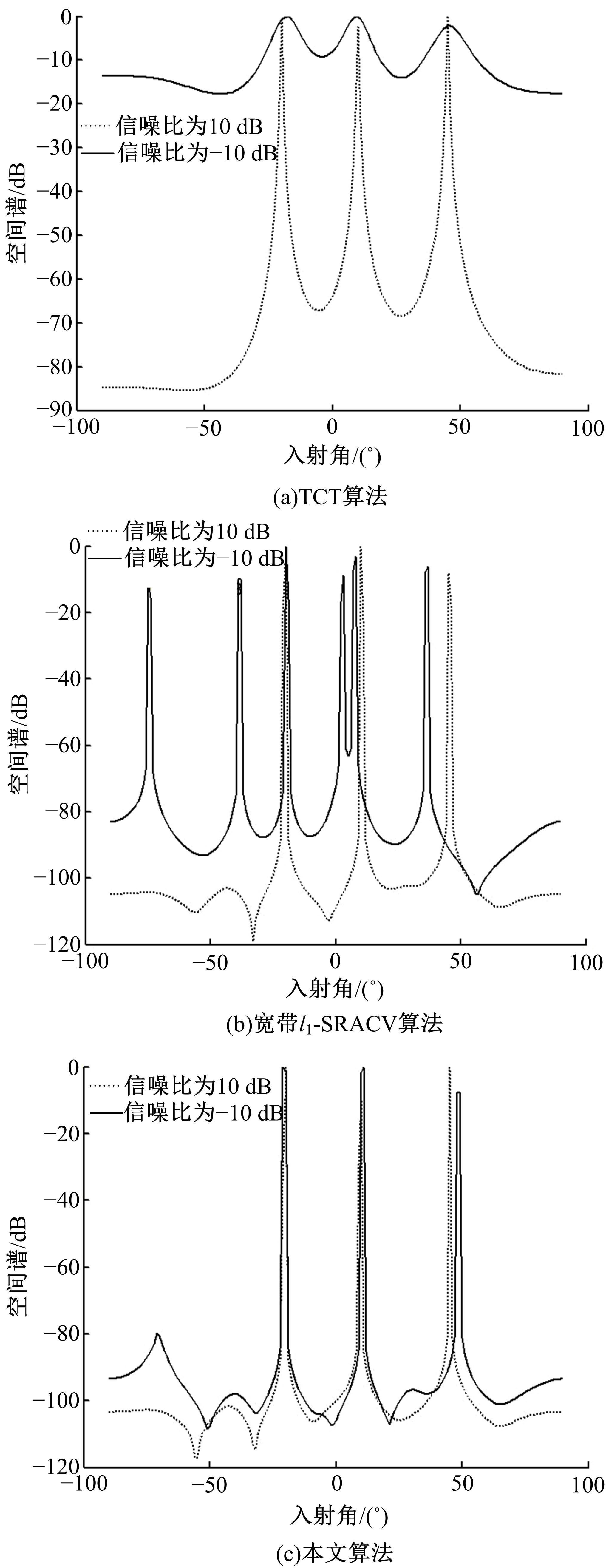
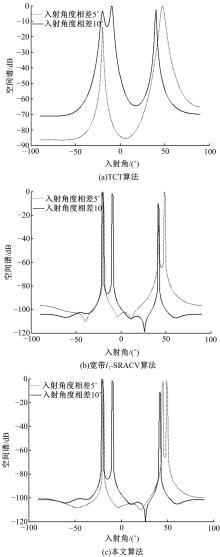
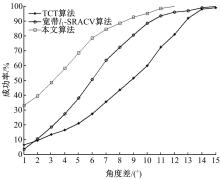
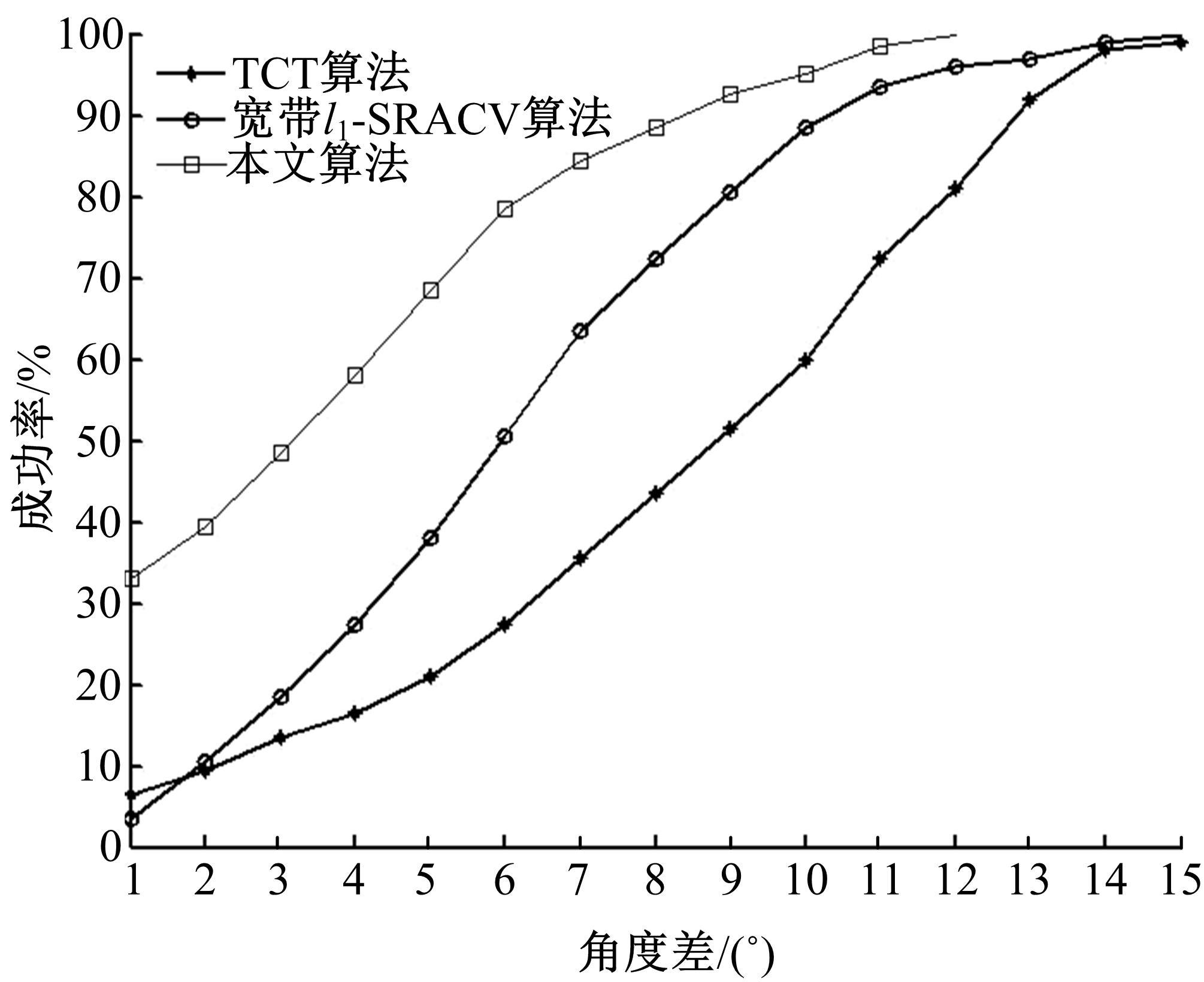
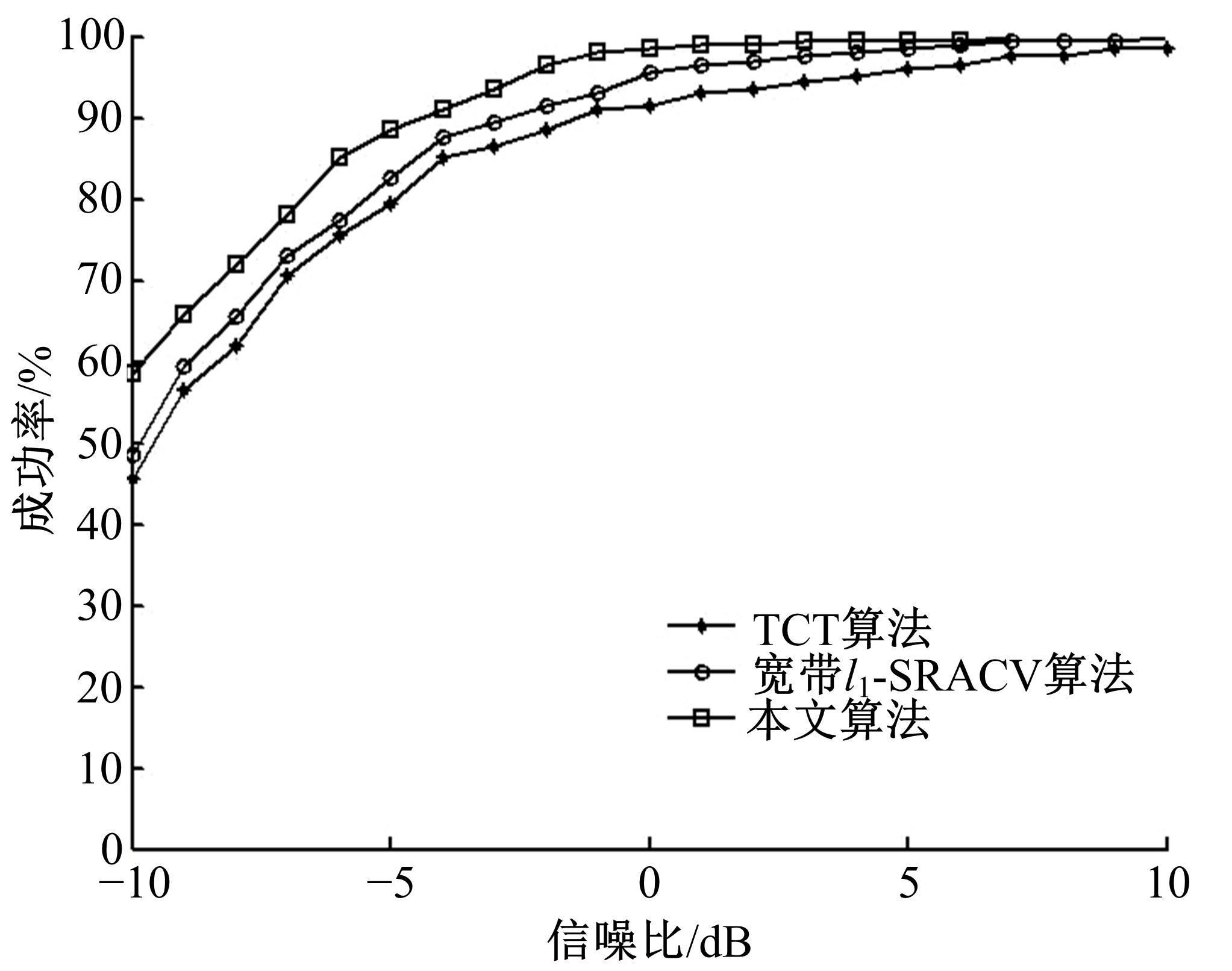
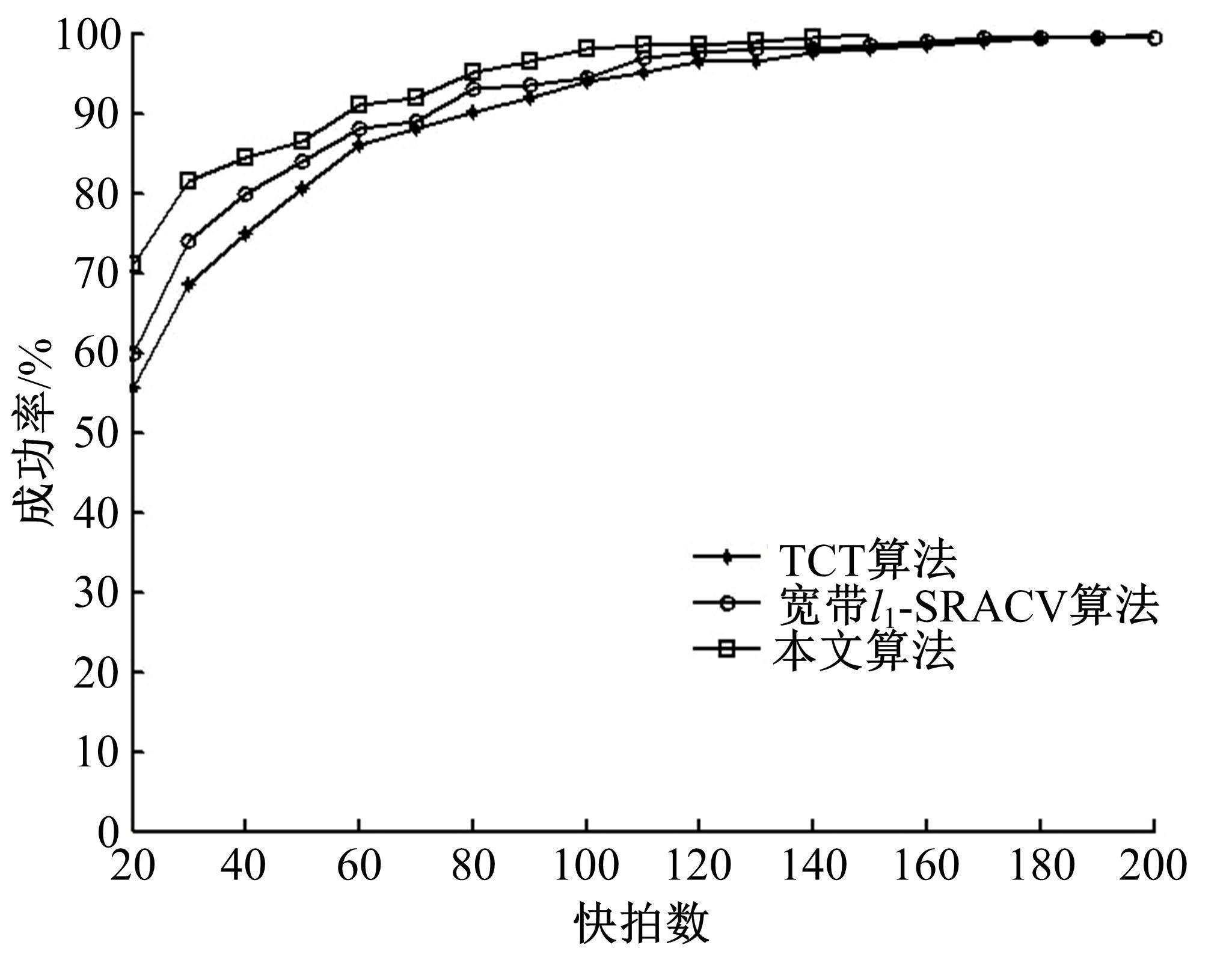
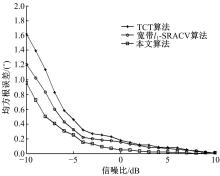
针对一维宽带信号波达方向（DOA）估计中聚焦变换算法需要角度预估值的问题，在双边相关变换算法基础上设计了一种无需角度预估值的DOA估计算法。首先，利用离散傅里叶变换（DFT）变换将宽带信号分解为若干个不同频点处的窄带数据模型。然后，通过本文改进的聚焦矩阵将不同频点处的窄带数据聚焦到同一参考频点，得到单一频率点处窄带信号模型。最后，采用改进阵列协方差矩阵稀疏迭代估计算法进行求解。理论研究和仿真实验结果表明，该方法在低信噪比和多快拍条件下比传统算法具有更高的估计精度和分辨率，且结合压缩感知理论有效降低了算法的运算量。

关键词: 信号与信息处理, 波达方向估计, 压缩感知, 聚焦变换

Abstract:

In order to solve the problem that the Direction of Arrival (DOA) estimation of one-dimensional wideband signal needs angle estimation, a DOA estimation algorithm without angle estimation is designed on the basis of bilateral correlation transform algorithm. Firstly, the wideband signal is decomposed into several narrow-band data models at different frequency points by using Discrete Fourier Transform (DFT). Secondly, the narrow-band data at different frequency points are focused on the same reference frequency point by the improved focusing matrix, thus, the narrow-band signal model at a single frequency point is obtained. Finally, the improved array covariance matrix sparse iterative estimation algorithm is used to solve the problem. Theoretical research shows that the proposed method has higher estimation accuracy and resolution than the traditional algorithm under the condition of low SNR and multiple snapshots, and the computational complexity of the algorithm is effectively reduced by combining with compressed sensing theory. The simulation results verify the reliability of the above conclusions.

Key words: signal and information processing, direction of arrival（DOA） estimation, compressive sensing, focusing transformatio

中图分类号:

TN911.7

窦慧晶,丁钢,高佳,梁霄. 基于压缩感知理论的宽带信号波达方向估计[J]. 吉林大学学报(工学版), 2021, 51(6): 2237-2245.

Hui-jing DOU,Gang DING,Jia GAO,Xiao LIANG. Wideband signal direction of arrival estimation based on compressed sensing theory[J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(6): 2237-2245.

图/表 9

表1

聚焦变换准则与聚焦矩阵对照表"

TCT算法	聚焦变换准则	$T (f j) ? A (f j, θ) S (f j) = A (f 0, θ) S (f 0)$
TCT算法	聚焦矩阵	$T (f j) = Q (f 0) Q H (f j)$
RSS算法	聚焦变换准则	$T (f j) ? A (f j, θ) = A (f 0, θ)$
RSS算法	聚焦矩阵	$T (f j) = V (f j, θ) U H (f j, θ)$
MTLS-CSSM 算法	聚焦变换准则	$T (f j) ? A (f j, θ) = A (f 0, θ)$
MTLS-CSSM 算法	聚焦矩阵	$T (f j) = A 0 (A 0 H A 0) - 1 / 2 (A j H A j) - 1 / 2 A j H$

表1

图1

图2

图3

图4

图5

图6

图7

表2

不同算法的运行时间对比"

算法	复杂度	运行时间/s
TCT	$O (M 3 + 2 N 3 M 3 + N 2 M 3)$	2.735 147
l₁-SRACV	$O (M 3 N 3)$	2.290 214
本文	$O (k N 3 M 3 + M 2)$	2.435 238

表2

参考文献 16

1	王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法[M]. 北京:清华大学出版社, 2004.
2	窦慧晶, 郭彩环, 张少飞, 等. 极化敏感阵列取向误差校正[J]. 吉林大学学报:工学版, 2016, 46(6): 2087-2093.
	Dou Hui-jing, Guo Cai-huan, Zhang Shao-fei, et al. Alignment error correction of polarization sensitive array[J]. Journal of Jilin University (Engineering and Technology Edition), 2016, 46 (6): 2087-2093.
3	Zhang Jia-cheng, Qiu Tian-shuang, Luan Sheng-yang, et al. Bounded non-linear covariance based ESPRIT method for noncircular signals in presence of impulsive noise[J]. Digital Signal Processing, 2019, 87: 104-111.
4	Herzog A, Habets E A P. Eigenbeam-ESPRIT for DOA-vector estimation[J]. IEEE Signal Processing Letters, 2019, 26(4): 572-576.
5	石要武, 石屹然, 陈淼, 等. 基于特征空间MUSIC算法的相干信号波达方向空间平滑估计[J]. 吉林大学学报: 工学版, 2017, 47(1):268-273.
	Shi Yao-wu, Shi Yi-ran, Chen Miao, et al. Spatial smoothing estimation of direction of arrival of coherent signals based on feature space music algorithm[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(1): 268-273.
6	Gong Bing, Xu Yi-tao, Liu Zhong-jun. A fast algorithm of modified ism for wideband direction finding[C]∥International Conference of China Communication, Nanning,China, 2010: 417-422.
7	Bilgehan B, Amr A. Fast detection and DOA estimation of the unknown wideband signal sources[J]. International Journal of Communication Systems, 2019, 32(11): No.e3968.
8	Wang H, Kaveh M. Coherent signal-subspace processing for the detection and estimation of angles of arrival of multiple wide-band sources[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1985, 33(4): 823-831.
9	Allam M, Moghaddamjoo A. Two-dimensional DFT projection for wideband direction-of-arrival estimation[J]. IEEE Transactions on Signal Processing, 1995, 43(7): 1728-1732.
10	Claudio E D, Parisi R. Weighted average of signal subspaces for robust wideband direction finding[J]. IEEE Transactions on Signal Processing, 2001, 49(10): 2179-2191.
11	石光明, 刘丹华, 高大化, 等. 压缩感知理论及其研究进展[J]. 电子学报, 2009, 37(5): 1070-1081.
	Shi Guang-ming, Liu Dan-hua, Gao Da-hua, et al. Compressed sensing theory and its research progress[J]. Acta electronica Sinica, 2009, 37 (5): 1070-1081.
12	Knee P. Sparse Representations for Radar with Matlab Examples[M]. America, San Rafae: Morgan & Claypool, 2012.
13	Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666.
14	Mathews C P, Zoltowski M D. Eigenstructure techniques for 2-D angle estimation with uniform circular arrays[J]. IEEE Transactions on Signal Processing, 1994, 42(9): 2395-2407.
15	窦慧晶, 梁霄, 张文倩. 压缩估计理论的二维DOA估计[J]. 北京工业大学学报, 2021, 47(3): 231-238.
	Dou Hui-jing, Liang Xiao, Zhang Wen-qian. Two dimensional DOA estimation based on compression estimation theory[J]. Journal of Beijing University of Technology, 2021, 47 (3): 231-238.
16	Ottersten B, Stoica P, Roy R. Covariance matching estimation techniques for array signal processing applications[J]. Digital Signal Process, 1998, 8(3): 185-210.

相关文章 15

[1]	金心宇,谢慕寒,孙斌. 基于半张量积压缩感知的粮情信息采集[J]. 吉林大学学报(工学版), 2021, 51(1): 379-385.
[2]	郭立民,陈鑫,陈涛. 基于AlexNet模型的雷达信号调制类型识别[J]. 吉林大学学报(工学版), 2019, 49(3): 1000-1008.
[3]	单泽彪,刘小松,史红伟,王春阳,石要武. 动态压缩感知波达方向跟踪算法[J]. 吉林大学学报(工学版), 2018, 48(6): 1938-1944.
[4]	陈涛, 崔岳寒, 郭立民. 适用于单快拍的多重信号分类改进算法[J]. 吉林大学学报(工学版), 2018, 48(3): 952-956.
[5]	单泽彪, 刘小松, 王春阳, 石屹然, 石要武. 相干/同向信号波达方向与多普勒频率的联合估计[J]. 吉林大学学报(工学版), 2017, 47(6): 1949-1956.
[6]	石要武, 陈淼, 单泽涛, 石屹然, 单泽彪. 基于特征空间MUSIC算法的相干信号波达方向空间平滑估计[J]. 吉林大学学报(工学版), 2017, 47(1): 268-273.
[7]	王新华, 欧阳继红, 庞武斌. 压缩编码孔径红外成像超分辨重建[J]. 吉林大学学报(工学版), 2016, 46(4): 1239-1245.
[8]	刘洲洲, 王福豹. 改进的离散混合蛙跳算法压缩感知信号重构及应用[J]. 吉林大学学报(工学版), 2016, 46(4): 1261-1268.
[9]	于华楠, 代芳琳, 苏天恺. 基于压缩感知的三相电能质量扰动信号压缩及分类新方法[J]. 吉林大学学报(工学版), 2016, 46(3): 964-971.
[10]	张轶, 达新宇, 褚振勇. 低密度奇偶校验码的压缩感知重构[J]. 吉林大学学报(工学版), 2015, 45(3): 985-990.
[11]	王宏志，王贤龙，周婷婷. 基于光滑0范数的图像分块压缩感知恢复算法[J]. 吉林大学学报(工学版), 2015, 45(1): 322-327.
[12]	田文飚, 芮国胜, 张海波, 王林. 下非均匀信息采集及重构[J]. 吉林大学学报(工学版), 2014, 44(4): 1209-1214.
[13]	贺岩, 赵晓晖. 理论的宽带多用户认知系统合作检测[J]. 吉林大学学报(工学版), 2014, 44(4): 1165-1170.
[14]	王好谦, 杜成立, 惠征. 一种新的多视点分布式视频编码算法[J]. 吉林大学学报(工学版), 2013, 43(增刊1): 225-229.
[15]	朱永贵, 刘平, 丛佳. 稀疏图像重构非凸Lp问题的分裂方法[J]. 吉林大学学报(工学版), 2013, 43(增刊1): 55-59.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed