随机载荷作用下的结构疲劳寿命区间分析

doi:10.13229/j.cnki.jdxbgxb20200502

摘要/Abstract

摘要：

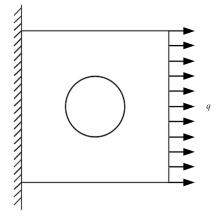
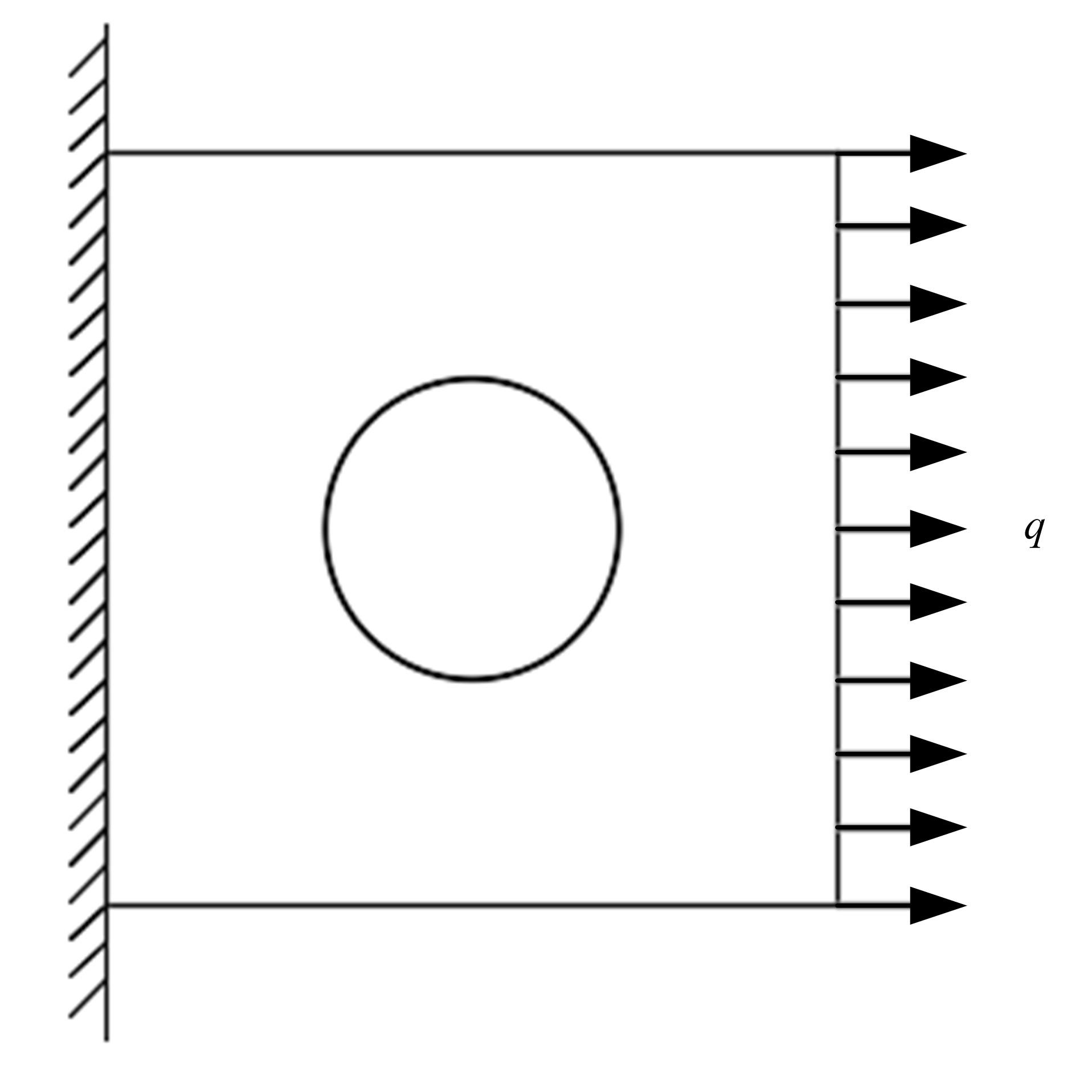
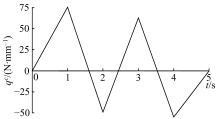
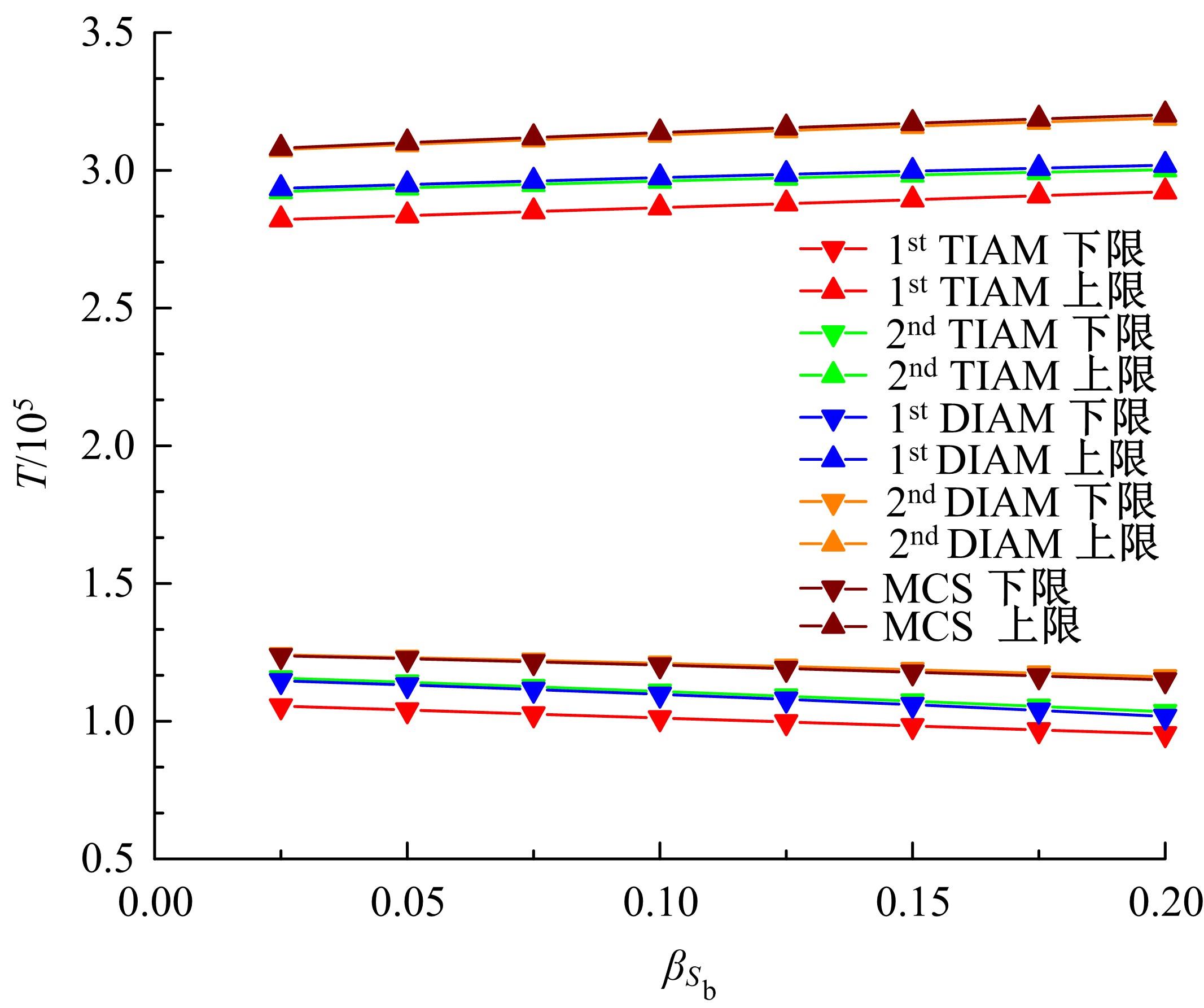
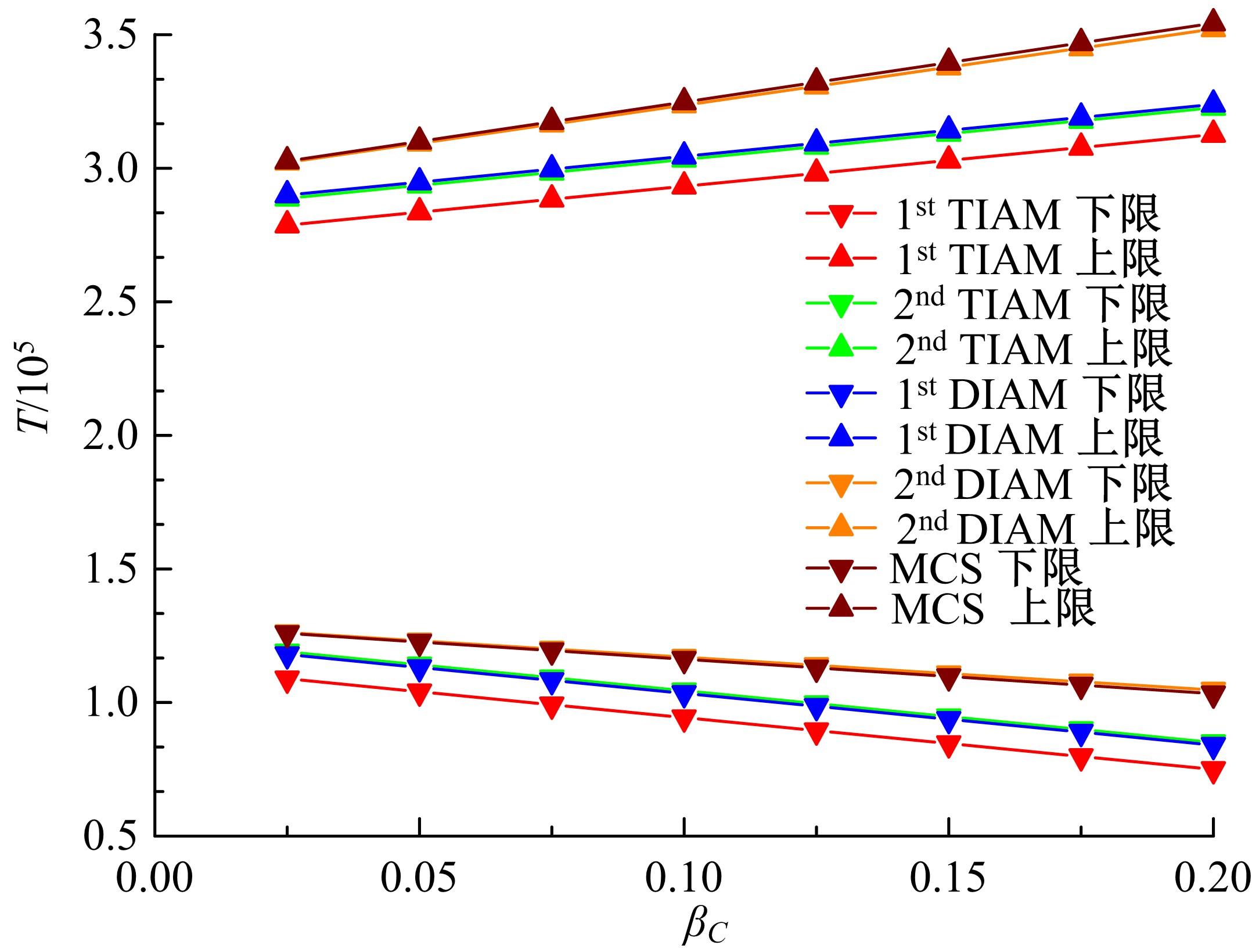
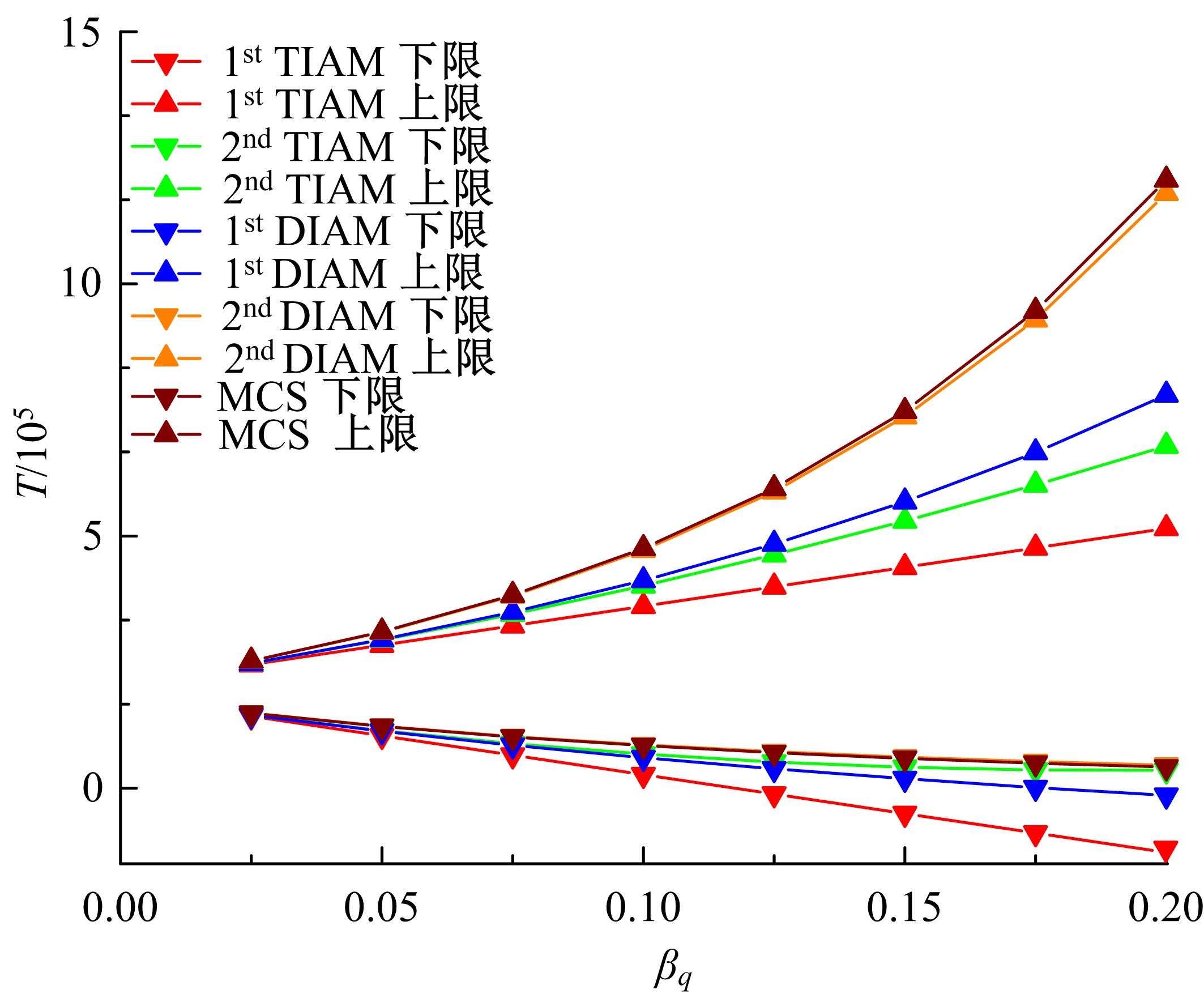
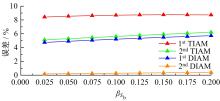
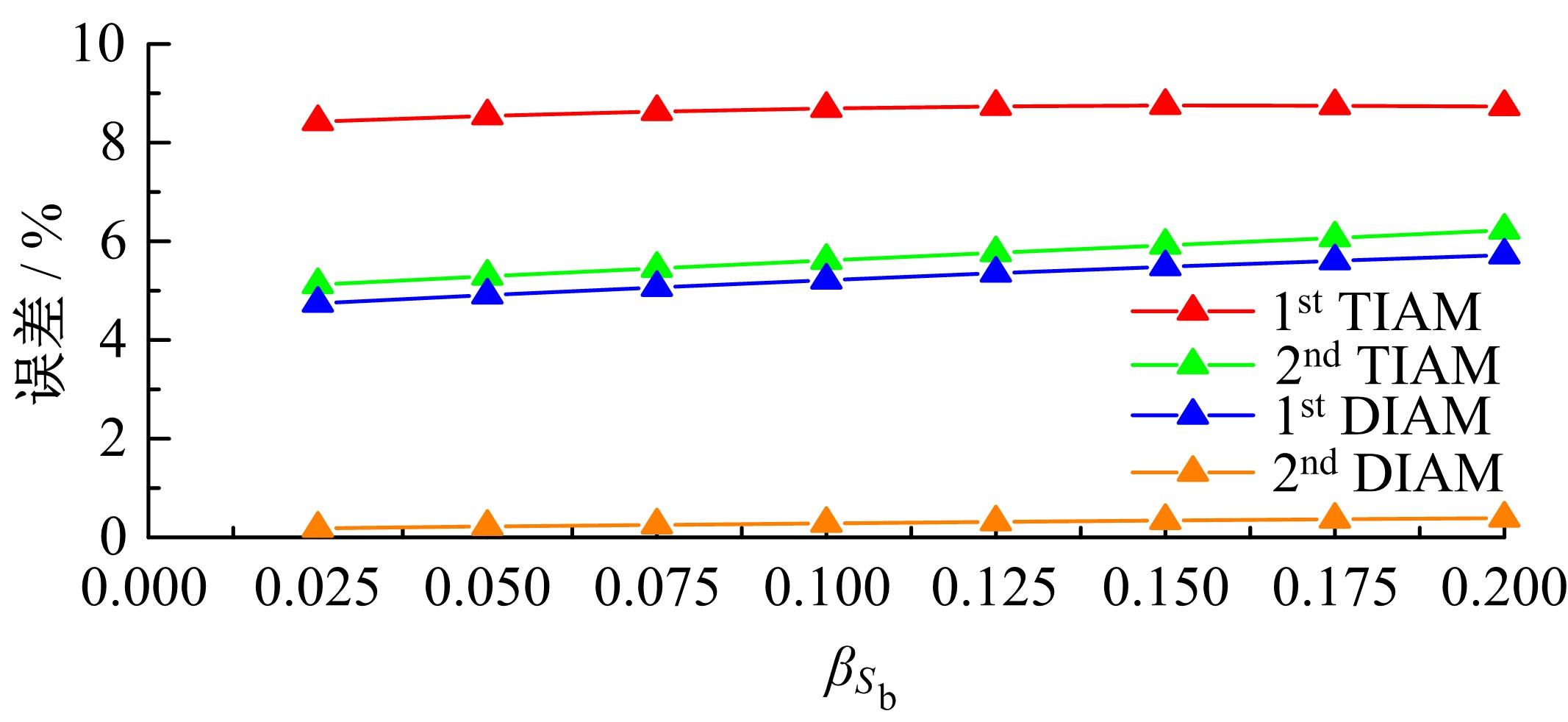
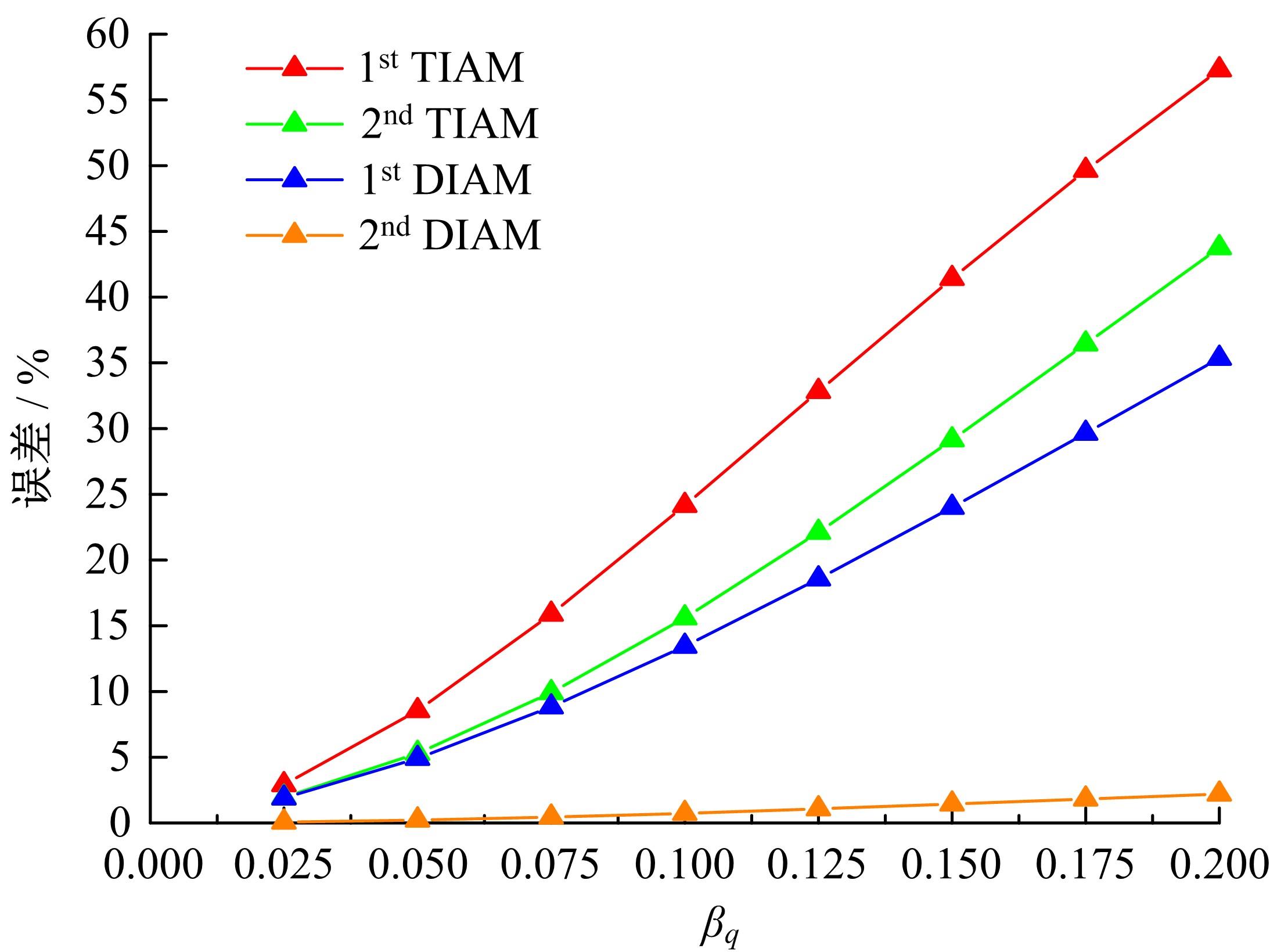
传统的概率方法分析结构疲劳寿命时，需要大量的样本以确定随变量的概率密度分布，而且概率密度函数较小的误差将会引起结构疲劳寿命较大的误差。针对这种情况，提出了一种随机载荷作用下结构疲劳寿命的区间分析模型。将影响结构疲劳寿命的不确定因素视为区间变量，给出了随机载荷作用下结构疲劳寿命的降维表达式，结合区间数学方法，得到了结构疲劳寿命的上限和下限。数值算例表明，与Taylor方法相比，基于降维算法的结构疲劳寿命区间分析方法具有较高的精度。对于强度极限和疲劳参数而言，一阶降维算法和二阶Taylor方法精度相当；而对于疲劳载荷，当其变化范围较大时，Taylor方法已经不能满足精度要求，而二阶降维算法仍然具有较高的计算精度和稳定性，其计算精度在一定范围内和遗传算法大致相当，但计算效率却远高于遗传算法。

关键词: 工程力学, 疲劳寿命, 随机载荷, 区间分析, 降维算法, Taylor展开法

Abstract:

Traditional probabilistic methods require large number of samples to determine the probability density distribution of the dependent variable when analyzing the fatigue life of structures， and a small error in the probability density function will cause a large error in the fatigue life of the structure. To solve this problem， an interval analysis model for structural fatigue life under random loads were proposed. The uncertain factors that affect the fatigue life of the structure were regarded as interval variables. The dimensionality reduction expression of the fatigue life of the structure under random load was given. Combined with the interval mathematical method， the upper and lower limits of the fatigue life of the structure were obtained. Numerical examples show that compared with the Taylor method， the structural fatigue life interval analysis method based on dimensionality reduction algorithm proposed in this paper has higher accuracy. For the strength limit and fatigue parameters， the first-order dimensionality reduction algorithm has almost the same accuracy compared with the second-order Taylor method. For fatigue loads， when the variation range is large， the Taylor method cannot meet the accuracy requirements， but the second-order dimensionality reduction algorithm is still steady. It has high calculation accuracy and stability. Its calculation accuracy is roughly equivalent to genetic algorithm within a certain range， but the calculation efficiency is much higher than that of the genetic algorithm.

Key words: engineering mechanics, fatigue life, random load, interval analysis, dimensionality reduction algorithm, Taylor expansion

中图分类号:

TP202.1

孟广伟,任传鑫,李锋,魏彤辉. 随机载荷作用下的结构疲劳寿命区间分析[J]. 吉林大学学报(工学版), 2022, 52(1): 46-52.

Guang-wei MENG,Chuan-xin REN,Feng LI,Tong-hui WEI. Interval analysis of structural fatigue life under random load[J]. Journal of Jilin University(Engineering and Technology Edition), 2022, 52(1): 46-52.

图/表 9

图1

图2

图3

图4

图5

图6

图7

图8

表1

参考文献 16

1	Karandikar J M, Kim N H, Schmitz T L. Prediction of remaining useful life for fatigue-damaged structures using Bayesian inference[J]. Engineering Fracture Mechanics, 2012, 96: 588-605.
2	Tsianika V, Geroulas V, Papadimitriou D, et al. A methodology of design for fatigue using an accelerated life testing approach with saddlepoint approximation[C]∥SAE International Paper, United States, 2019: 1-13.
3	李亚波, 宋清源, 杨凯, 等. 试样疲劳性能尺度效应的概率控制体积方法[J]. 力学学报, 2019, 51(5): 1363-1371.
	Li Ya-bo, Song Qing-yuan, Yang Kai, et al. Probabilistic control volume method for the size effect of specimen fatigue performance [J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(5): 1363-1371.
4	孙祝岭. Birnbaum-Saunders疲劳寿命分布参数的回归估计方法[J]. 兵工学报, 2010, 31(9): 1259-1262.
	Sun Zhu-ling. Regression estimation of the parameters of the Birnbaum-Saunders fatigue life distribution[J]. Acta Armamentarii, 2010, 31(9): 1259-1262.
5	Moore R E. Methods and Applications of Interval Analysis[M]. Philadephia: SIAML, 1979.
6	Long X Y, Jiang C, Liu K, et al. An interval analysis method for fatigue crack growth life prediction with uncertainty [J]. Computers and Structures, 2018, 210(2018): 1-11.
7	王军, 邱志平, 金延伟. 疲劳寿命的区间名义应力法及灵敏度分析[J]. 飞机设计, 2012, 32(6): 42-46.
	Wang Jun, Qiu Zhi-ping, Jin Yan-wei. Nominal stress method of fatigue life and sensitivity analysis[J]. Aircraft Design, 2012, 32(6): 42-46.
8	陈小月, 文桂林, 刘杰,等. 基于泛灰数的结构疲劳寿命区间估计方法[J]. 计算机仿真, 2017, 34(4): 245-249.
	Chen Xiao-yue, Wen Gui-lin, Liu Jie, et al. Estimation approach of structure fatigue life based on universal grey number[J]. Computer Simulation, 2017, 34(4): 245-249.
9	邱志平, 王晓军. 结构疲劳寿命的区间估计[J]. 力学学报, 2005(5): 653-657.
	Qiu Zhi-ping, Wang Xiao-jun. Interval estimation for structural fatigue lifetime [J]. Chinese Journal of Theoretical and Applied Mechanics, 2005(5): 653-657.
10	孙作振, 孟广伟, 李锋, 等. 基于二阶区间摄动法的结构疲劳寿命估计[J]. 东北大学学报:自然科学版, 2013, 34(): 75-78.
	Sun Zuo-zhen, Meng Guang-wei, Li Feng, et al. Structure fatigue life estimation based on the second-order interval perturbation method[J]. Journal of Northeastern University (Natural Science), 2013, 34(Sup.2): 75-78.
11	李锋, 孟广伟, 沙丽荣. 考虑模糊失效准则的结构疲劳寿命可靠性[J]. 航空学报, 2009, 30(12): 2316-2321.
	Li Feng, Meng Guang-wei, Sha Li-rong. Reliability analysis of structural fatigue life under fuzzy failure criteria[J].Acta Aeronautica Et Astronautica Sinica, 2009, 30(12): 2316-2321.
12	Rahman S. A dimensional decomposition method for stochastic fracture mechanics[J]. Engineering Fracture Mechanics, 2006, 73(15): 2093-2109.
13	Li G, Zhang K. A combined reliability analysis approach with dimension reduction method and maximum entropy method[J]. Structural and Multidisciplinary Optimization, 2011, 43(1): 121-143.
14	付酥昇.ANSYS ncode designlife: 疲劳分析基础与实例教程[M].北京:人民邮电出版社, 2020.
15	Ponticelli G S, Guarino S, Giannini O. An optimal genetic algorithm for fatigue life control of medium carbon steel in laser hardening process[J]. Applied Sciences-Basel, 2020, 10(1401): 1-14.
16	闫楚良, 郝云霄, 刘克格. 基于遗传算法优化的BP神经网络的材料疲劳寿命预测[J]. 吉林大学学报:工学版, 2014, 44(6): 1710-1715.
	Yan Chu-liang, Hao Yun-xiao, Liu Ke-ge. Fatigue life prediction of materials based on BP neural networks optimized by genetic algorithm[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(6): 1710-1715.

相关文章 15

[1]	彭勇,杨汉铎,陆学元,李彦伟. 基于离散元法的空隙特征对沥青混合料虚拟剪切疲劳寿命的影响[J]. 吉林大学学报(工学版), 2021, 51(3): 956-964.
[2]	李碧雄,廖桥,章一萍,周练,隗萍,刘侃. 超高强钢筋工程用水泥基复合材料梁受弯计算理论[J]. 吉林大学学报(工学版), 2019, 49(4): 1153-1161.
[3]	尼颖升,孙启鑫,马晔,徐栋,刘超. 基于空间网格分析的多箱室波形钢腹板组合梁腹板剪力分配[J]. 吉林大学学报(工学版), 2018, 48(6): 1735-1746.
[4]	毛宇泽, 王黎钦. 鼠笼支撑一体化结构对薄壁球轴承承载性能的影响[J]. 吉林大学学报(工学版), 2018, 48(5): 1508-1514.
[5]	王春生, 邹丽, 杨鑫华. 基于邻域粗糙集的铝合金焊接接头疲劳寿命影响因素分析[J]. 吉林大学学报(工学版), 2017, 47(6): 1848-1853.
[6]	闫亚宾, 王晓媛, 万强. 纳米尺度界面低周疲劳破坏行为[J]. 吉林大学学报(工学版), 2017, 47(4): 1201-1206.
[7]	王国林, 孙砚田, 梁晨, 杨建, 周海超. 应用满应力理论的轮胎轮廓设计[J]. 吉林大学学报(工学版), 2017, 47(2): 365-372.
[8]	陈江义, 刘保元. 纤维断裂损伤对复合材料板中导波频散特性的影响[J]. 吉林大学学报(工学版), 2017, 47(1): 180-184.
[9]	孟广伟, 冯昕宇, 周立明, 李锋. 基于降维算法的结构可靠性分析[J]. 吉林大学学报(工学版), 2017, 47(1): 174-179.
[10]	曹珊珊, 雷俊卿. 考虑区间不确定性的钢结构疲劳寿命分析[J]. 吉林大学学报(工学版), 2016, 46(3): 804-810.
[11]	蒋荣超, 王登峰, 秦民, 蒋永峰. 基于疲劳寿命的轿车后悬架扭转梁轻量化设计[J]. 吉林大学学报(工学版), 2016, 46(1): 35-42.
[12]	邢保英, 何晓聪, 王玉奇, 邓成江. 多铆钉自冲铆接头力学性能机理[J]. 吉林大学学报(工学版), 2015, 45(5): 1488-1494.
[13]	杨慧艳, 何晓聪, 周森. 压印接头强度的有限元模型及理论计算方法[J]. 吉林大学学报(工学版), 2015, 45(3): 864-871.
[14]	邓成江，何晓聪，邢保英，王玉奇，曾凯，丁燕芳. 铝与铜异质板材自冲铆搭接接头的力学性能[J]. 吉林大学学报(工学版), 2015, 45(2): 473-480.
[15]	闫楚良, 郝云霄, 刘克格. 基于遗传算法优化的BP神经网络的材料疲劳寿命预测[J]. 吉林大学学报(工学版), 2014, 44(6): 1710-1715.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

β_q	MCS	二阶降维算法		遗传算法
β_q	中值/10⁵	中值/10⁵	误差/%	中值/10⁵	误差/%
0.025	2.006	2.005	0.0	2.003	0.1
0.050	2.164	2.162	0.1	2.161	0.1
0.075	2.423	2.419	0.2	2.413	0.4
0.100	2.801	2.790	0.4	2.790	0.4
0.125	3.325	3.302	0.7	3.298	0.8
0.150	4.033	3.992	1.0	4.001	0.8
0.175	4.980	4.909	1.4	4.942	0.8
0.200	6.240	6.126	1.8	6.192	0.8