改进的鸡群优化算法

doi:10.13229/j.cnki.jdxbgxb20181268

摘要/Abstract

摘要：

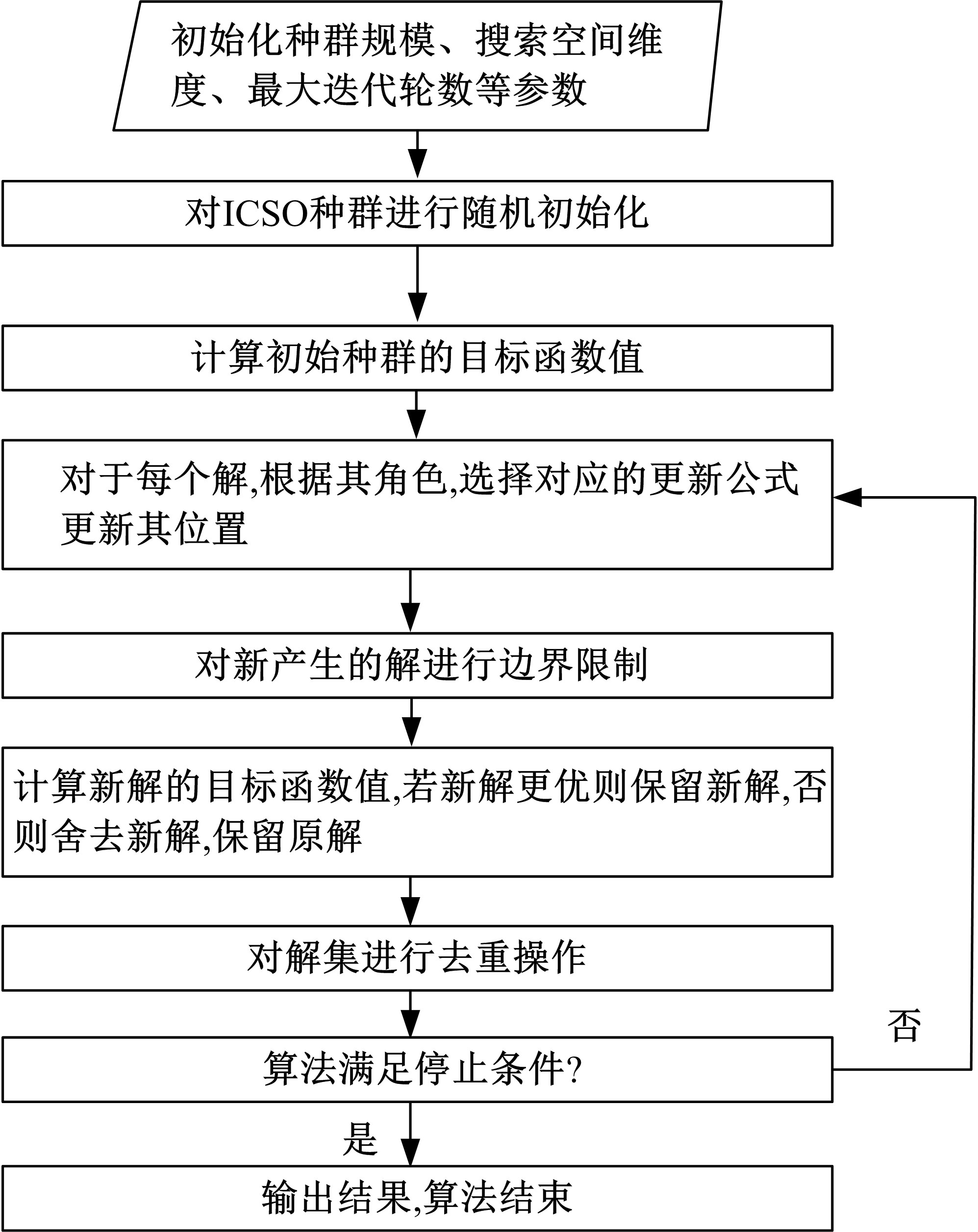
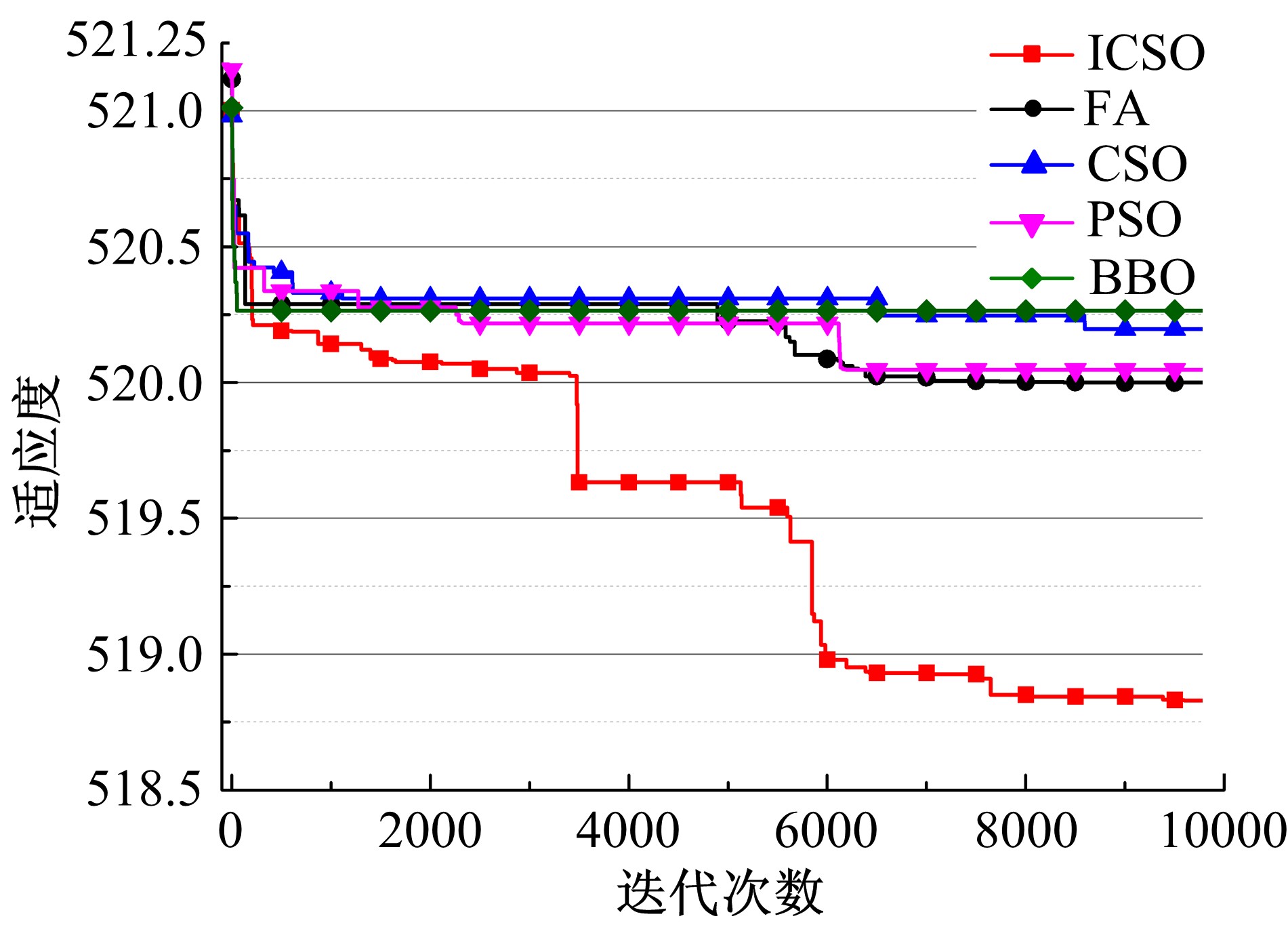
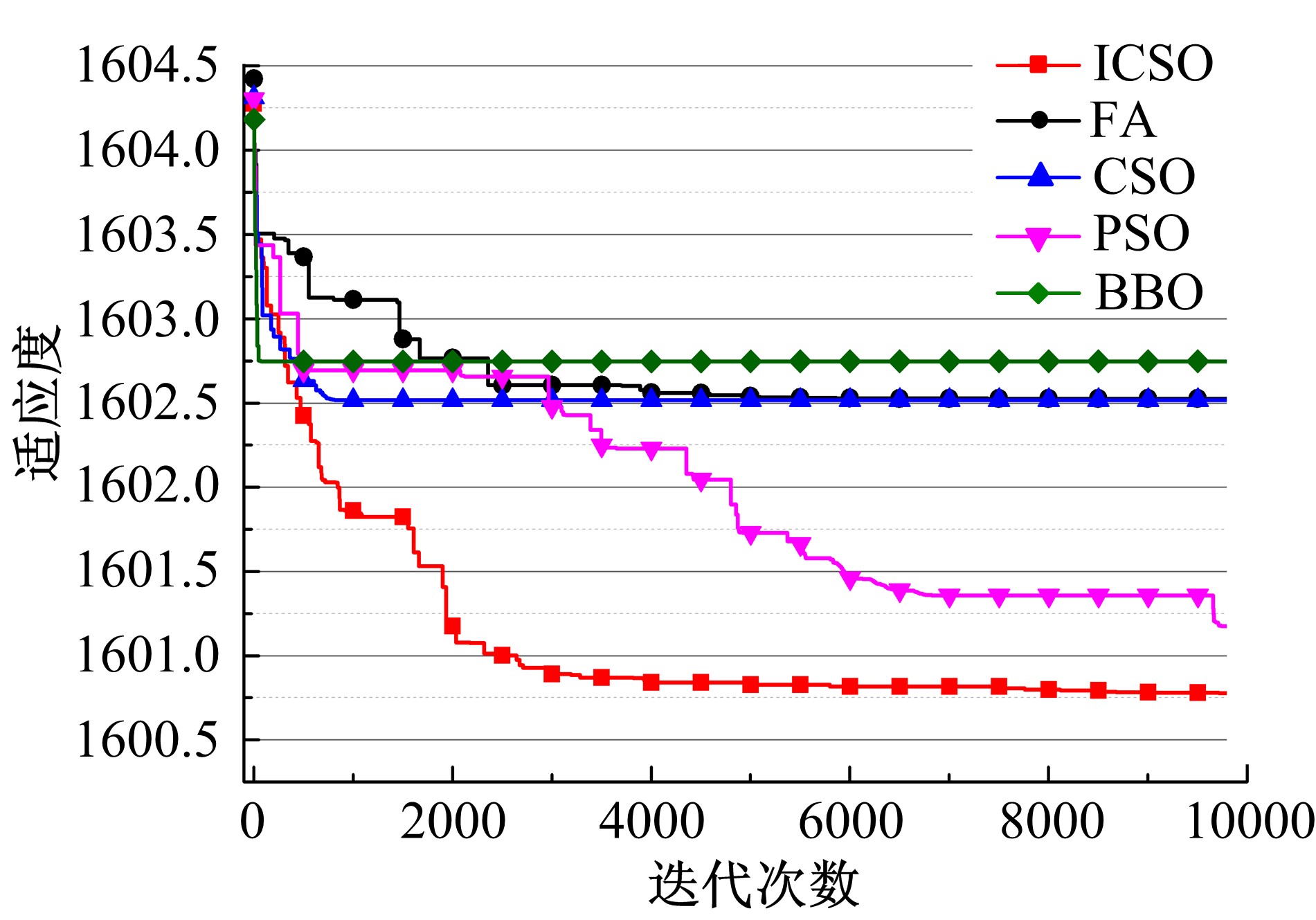
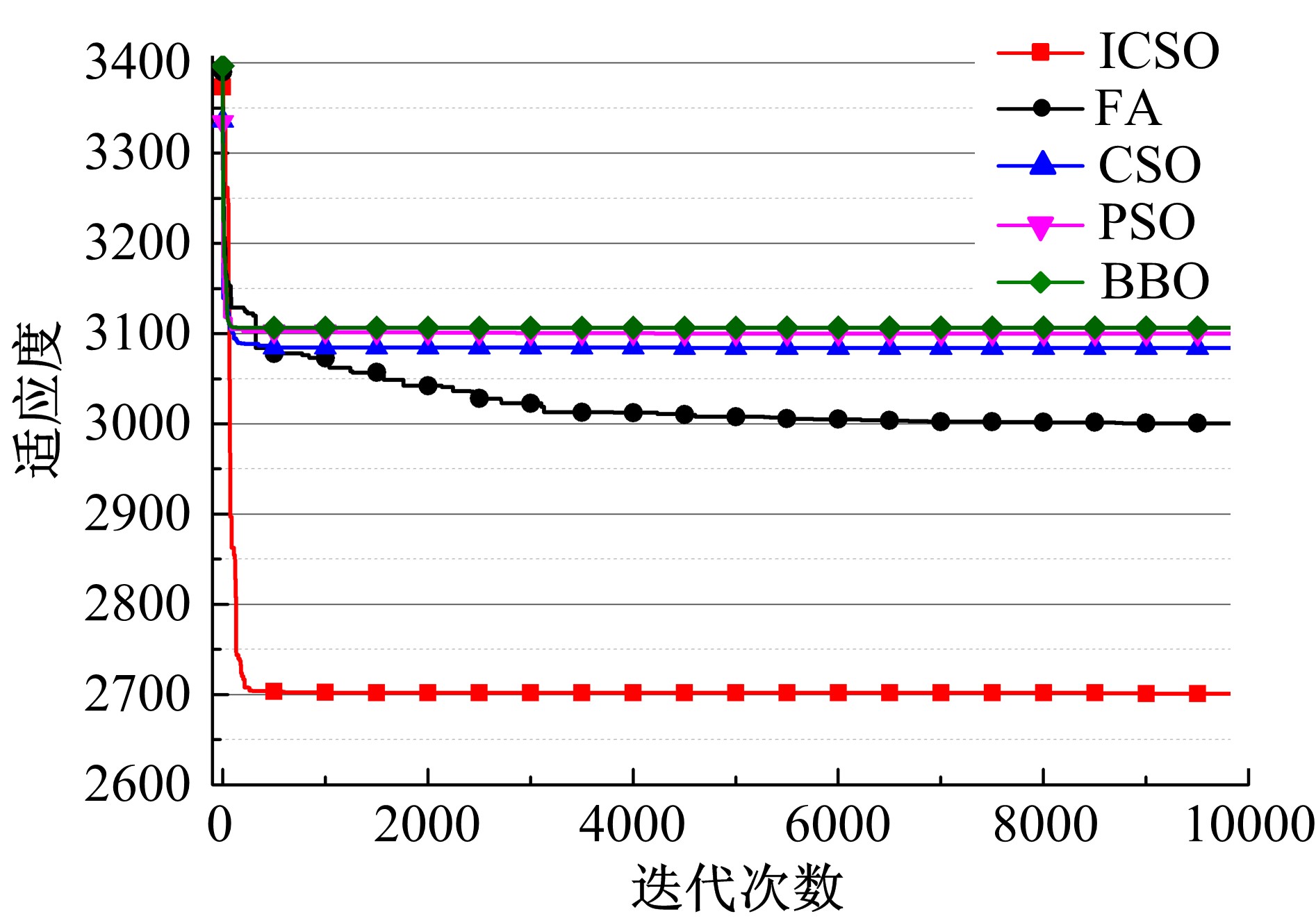
针对鸡群优化算法中解的更新效率较低且缺乏探索性等问题，提出了一种改进的鸡群优化算法。该算法基于标准鸡群优化算法的种群分组更新机制，并借鉴狼群优化算法和粒子群优化算法的思想，引入改进因子和去重操作算子分别用以增强算法的寻优能力和提高种群的多样性。通过与其他4种算法在CEC 2014测试函数集上进行比较，结果表明本文算法在绝大多数测试函数上均表现出了良好的优化效果，在求解精度及收敛速度方面也优于其他算法。

关键词: 计算机应用, 鸡群优化算法, 收敛速度, 功能优化

Abstract:

Based on the hierarchy mechanism of the conventional chicken swarm optimization (CSO) algorithm, an improved chicken swarm optimization (ICSO) algorithm is proposed to enhance the solution accuracy and the convergence rate of the conventional CSO algorithm. The ICSO algorithm introduces several improved factors that learned from the grey wolf optimizer (GWO) and the particle swarm optimization (PSO), to extend the searching ability of the algorithm. Moreover, a duplicate remove operator is also introduced to improve the diversity of the population. Experimental results show that the accuracy of the solution and the convergence rate of the proposed algorithm are better than other benchmark algorithms.

Key words: computer applications, chicken swarm optimization(CSO) algorithm, convergence rate, function optimization

中图分类号:

TP301

李宾,申国君,孙庚,郑婷婷. 改进的鸡群优化算法[J]. 吉林大学学报(工学版), 2019, 49(4): 1339-1344.

Bin LI,Guo⁃jun SHEN,Geng SUN,Ting⁃ting ZHENG. Improved chicken swarm optimization algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(4): 1339-1344.

图/表 5

图1

表1

基准函数测试结果"

函数	ICSO算法	FA算法	CSO算法	PSO算法	BBO算法
最优总数	21	11	7	17	9
f₁	5.55e+04 ± 4.75e+04	1.78e+03 ± 1.12e+04	2.91e+06 ± 2.44e+06	2.18e+03 ± 1.93e+04	2.60e+05 ± 2.26e+06
f₂	1.08e+03 ± 2.71e+02	2.96e+02 ± 2.23e+03	1.25e+07 ± 7.15e+07	1.26e+03 ± 4.20e+02	5.02E+03 ± 1.09e+05
f₃	7.71e+02 + 2.86e+02	3.00e+02 ± 3.21e-04	1.45e+03 ± 6.71e+02	3.00e+02 ± 5.75e-03	1.01e+04 ± 3.39e+03
f₄	4.00e+02 ± 1.88e-01	4.35e+02 ± 8.24e+00	4.41e+02 ± 8.99e+00	4.00e+02 ± 1.70e+01	4.35e+02 ±1.16e+01
f₅	5.19e+02 ± 5.97e+00	5.20e+02 ± 2.80e+00	5.20e+02 ± 3.47e+00	5.20e+02 ± 5.48e+00	5.20e+02 ± 7.66e-02
f₆	6.00e+02 ± 1.24e+00	6.00e+02 ± 2.23e-02	6.05e+02 ± 8.97e-01	6.00e+02 ± 9.31e-01	6.02e+02 ± 1.19e+00
f₇	7.00e+02 ± 1.00e-02	7.00e+02 ± 4.89e-02	7.07e+02 ± 2.21e+00	7.00e+02 ± 3.53e-02	7.00e+02 ± 1.14e-01
f₈	8.03e+02 ± 3.77e+00	8.11e+02 ± 3.07e+00	8.12e+02 ± 3.27e+00	8.00e+02 ± 1.61e-14	8.01e+02 ± 1.20e+00
f₉	9.06e+02 ± 4.06e+00	9.07e+02 ± 3.23e+00	9.12e+02 ± 3.43e+00	9.07e+02 ± 1.71e+00	9.14e+02 ± 4.69e+00
f₁₀	1.06e+03 ± 2.36e+02	1.24e+03 ± 1.68e+02	1.26e+03 ± 8.50e+01	1.13e+03 ± 6.20e+01	1.03e+03 ± 1.18e+01
f₁₁	1.46e+03 ± 2.01e+02	1.69e+03 ± 1.68e+02	1.66e+03 ± 1.72e+02	1.48e+03 ± 1.29e+02	2.02e+03 ± 2.10e+02
f₁₂	1.20e+03 ± 3.14e-02	1.20e+03 ± 6.00e-03	1.20e+03 ± 1.17e-01	1.20e+03 ± 5.62e-02	1.20e+03 ± 2.40e-01
f₁₃	1.30e+03 ± 6.97e-02	1.30e+03 ± 1.91e-02	1.30e+03 ± 8.45e-02	1.30e+03 ± 4.53e-02	1.30e+03 ± 9.47e-02
f₁₄	1.40e+03 ± 7.79e-02	1.40e+03 ± 3.86e-02	1.40e+03 ± 1.63e-01	1.40e+03 ± 2.26e-02	1.40e+03 ± 7.76e-02
f₁₅	1.50e+03 ± 1.81e-01	1.50e+03 ± 1.48e-01	1.50e+03 ± 4.48e-01	1.50e+03 ± 2.38e-01	1.50e+03 ± 5.68e-01
f₁₆	1.60e+03 ± 3.18e-01	1.60e+03 ± 4.33e-01	1.60e+03 ± 3.30e-01	1.60e+03 ± 5.77e-01	1.60e+03 ± 4.10e-01
f₁₇	2.16e+03 ± 2.47e+02	2.45e+03 ± 3.62e+02	3.87e+03 ± 2.80e+03	3.89e+03 ± 1.23e+03	1.21e+04 ± 3.07e+05
f₁₈	1.91e+03 ± 6.00e+01	6.54e+03 ± 3.13e+00	8.68e+03 ± 2.71e+03	2.43e+03 ± 3.90e+03	4.02e+03 ± 5.01e+04
f₁₉	1.90e+03 ± 3.48e-01	1.90e+03 ± 6.41e-01	1.90e+03 ± 8.40e-01	1.90e+03 ± 6.95e-01	1.90e+03 ± 4.52e-01
f₂₀	2.10e+03 ± 6.34e+01	2.02e+03 ± 2.25e+01	2.07e+03 ± 1.42e+03	2.01e+03 ± 2.09e+00	2.56e+04 ± 2.78e+04
f₂₁	2.36e+03 ± 6.19e+00	2.55e+03 ± 2.10e+02	2.37e+03 ± 7.96e+02	2.22e+03 ± 5.13e+01	1.20e+04 ± 5.65e+04
f₂₂	2.22e+03 ± 7.12e+01	2.22e+03 ± 5.66e+01	2.23e+03 ± 3.30e+01	2.20e+03 ± 1.00e+01	2.22e+03 ± 4.51e+01
f₂₃	2.40e+03 ± 7.12e+01	2.63e+03 ± 1.26e-07	2.63e+03 ± 1.91e+01	2.63e+03 ± 1.02e-12	2.63e+03 ± 1.28e-01
f₂₄	2.52e+03 ± 4.68e+00	2.52e+03 ± 4.87e+00	2.54e+03 ± 1.24e+01	2.51e+03 ± 4.04e+00	2.53e+03 ± 7.41e+00
f₂₅	2.61e+03 ± 9.46e+00	2.62e+03 ± 1.79e+01	2.68e+03 ± 9.89e+00	2.70e+03 ± 3.72e+01	2.70e+03 ± 9.47e-02
f₂₆	2.70e+03 ± 4.46e-02	2.70e+03 ± 1.62e-02	2.70e+03 ± 4.45e-02	2.70e+03 ± 4.31e-02	2.70e+03 ± 2.60e+01
f₂₇	2.70e+03 ± 6.15e+01	3.00e+03 ± 1.37e+02	3.08e+03 ± 1.86e+02	3.10e+03 ± 1.67e+02	3.11e+03 ± 1.84e+02
f₂₈	3.00e+03 ± 6.35e+01	3.16e+03 ± 1.43e+02	3.19e+03 ± 1.20e+01	3.19e+03 ± 7.26e+01	3.17e+03 ± 2.69e+01
f₂₉	3.14e+03 ± 9.52e+01	3.33e+03 ± 2.41e+05	3.67e+03 ± 2.30e+02	3.23e+03 ±8.25e+05	3.57e+03 ± 5.15e+02
f₃₀	3.47e+03 ± 6.87e+01	3.75e+03 ± 1.59e+02	3.92e+03 ± 3.03e+02	3.63e+03 ± 2.46e+02	3.65e+03 ± 2.59e+02

表1

图2

图3

图4

参考文献 15

1	MengX, LiuY, GaoX, et al. A New Bio-inspired Algorithm: Chicken Swarm Optimization[M]. Berlin: Springer International Publishing, 2014.
2	BanerjeeS, ChattopadhyayS. Improved serially concatenated convolution turbo code (SCCTC) using chicken swarm optimization[C]∥IEEE Power, Communication and Information Technology Conference (PCITC), Bhubaneswar, India, 2015.
3	HafezA I, ZawbaaH M, EmaryE, et al. An innovative approach for feature selection based on chicken swarm optimization[C]∥IEEE International Conference on Soft Computing & Pattern Recognition, Tokyo, Japan, 2016.
4	ChenP, MaoY. Wireless sensor network node localization algorithm based on chicken swarm optimization and multi-power mobile anchor[C]∥The 3rd International Conference on Materials Engineering, Manufacturing Technology and Control, Taiyuan, China, 2016.
5	MuY, ZhangL, ChenX, et al. Optimal trajectory planning for robotic manipulators using chicken swarm optimization[C]∥IEEE International Conference on Intelligent Human-machine Systems & Cybernetics, Chengdu, China, 2016.
6	Roslina, ZarlisM, YantoI T R, et al. A framework of training ANFIS using chicken swarm optimization for solving classification problems[C]∥IEEE International Conference on Informatics & Computing, Mataram, Indonesia，2017.
7	YiZ, LiuJ, WangS, et al. PAPR reduction technology based on CSO algorithm in CO-OFDM system[C]∥The International Conference on Optical Communications & Networks, Wuzhen, China, 2017.
8	WuYu, YanBo, QuXiang-ju. Improved chicken swarm optimization method for reentry trajectory optimization[J]. Mathematical Problems in Engineering, 2018(2): 1-13.
9	WuZ, YuD, KangX. Application of improved chicken swarm optimization for MPPT in photovoltaic system[J]. Optimal Control Applications and Methods, 2018, 39(2):1029-1042.
10	HanM, LiuS. An improved binary chicken swarm optimization algorithm for solving 0-1 Knapsack problem[C]∥The 13th International Conference on Computational Intelligence and Security (CIS), Hong Kong, 2017.
11	Yang, S X. Firefly algorithm, stochastic test functions and design optimisation[J]. International Journal of Bio-inspired Computation, 2010,2(2):78⁃84.
12	王沈娟, 高晓智. 萤火虫算法研究综述[J]. 微型机与应用, 2015, 34(8):8-11.
	WangShen-juan, GaoXiao-zhi. A survey of firefly algorithm[J]. Microcomputer and Its Applications, 2015, 34(8):8-11.
13	MirjaliliS, MirjaliliS M, LewisA. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69(3):46-61.
14	龙文, 赵东泉, 徐松金, 等. 求解约束优化问题的改进灰狼优化算法[J]. 计算机应用, 2015, 35(9):2590-2595.
	LongWen, ZhaoDong-quan, XuSong-jin，et al. Improved grey wolf optimization algorithm for constrained optimization problem[J]. Journal of Computer Applications, 2015, 35(9):2590-2595.
15	LiangJing, QuB Y, Suganthan PonnuthuraiN, et al. Problem definitions and evaluation criteria for the CEC 2013 special session and competition on single objective real-parameter numerical optimization[C]∥IEEE Congress on Evolutionary Computation,Beijing, China， 2014.

相关文章 15

[1]	李雄飞,宋璐,张小利. 基于协同经验小波变换的遥感图像融合[J]. 吉林大学学报(工学版), 2019, 49(4): 1307-1319.
[2]	孙延君,申铉京,陈海鹏,赵永哲. 基于局部平面线性点的翻拍图像鉴别算法[J]. 吉林大学学报(工学版), 2019, 49(4): 1320-1328.
[3]	刘元宁,刘帅,朱晓冬,霍光,丁通,张阔,姜雪,郭书君,张齐贤. 基于决策粒子群优化与稳定纹理的虹膜二次识别[J]. 吉林大学学报(工学版), 2019, 49(4): 1329-1338.
[4]	王楠,李金宝,刘勇,张玉杰,钟颖莉. TPR⁃TF:基于张量分解的时间敏感兴趣点推荐模型[J]. 吉林大学学报(工学版), 2019, 49(3): 920-933.
[5]	刘富,宗宇轩,康冰,张益萌,林彩霞,赵宏伟. 基于优化纹理特征的手背静脉识别系统[J]. 吉林大学学报(工学版), 2018, 48(6): 1844-1850.
[6]	王利民,刘洋,孙铭会,李美慧. 基于Markov blanket的无约束型K阶贝叶斯集成分类模型[J]. 吉林大学学报(工学版), 2018, 48(6): 1851-1858.
[7]	金顺福,王宝帅,郝闪闪,贾晓光,霍占强. 基于备用虚拟机同步休眠的云数据中心节能策略及性能[J]. 吉林大学学报(工学版), 2018, 48(6): 1859-1866.
[8]	赵东,孙明玉,朱金龙,于繁华,刘光洁,陈慧灵. 结合粒子群和单纯形的改进飞蛾优化算法[J]. 吉林大学学报(工学版), 2018, 48(6): 1867-1872.
[9]	刘恩泽,吴文福. 基于机器视觉的农作物表面多特征决策融合病变判断算法[J]. 吉林大学学报(工学版), 2018, 48(6): 1873-1878.
[10]	欧阳丹彤, 范琪. 子句级别语境感知的开放信息抽取方法[J]. 吉林大学学报(工学版), 2018, 48(5): 1563-1570.
[11]	刘富, 兰旭腾, 侯涛, 康冰, 刘云, 林彩霞. 基于优化k-mer频率的宏基因组聚类方法[J]. 吉林大学学报(工学版), 2018, 48(5): 1593-1599.
[12]	桂春, 黄旺星. 基于改进的标签传播算法的网络聚类方法[J]. 吉林大学学报(工学版), 2018, 48(5): 1600-1605.
[13]	刘元宁, 刘帅, 朱晓冬, 陈一浩, 郑少阁, 沈椿壮. 基于高斯拉普拉斯算子与自适应优化伽柏滤波的虹膜识别[J]. 吉林大学学报(工学版), 2018, 48(5): 1606-1613.
[14]	车翔玖, 王利, 郭晓新. 基于多尺度特征融合的边界检测算法[J]. 吉林大学学报(工学版), 2018, 48(5): 1621-1628.
[15]	赵宏伟, 刘宇琦, 董立岩, 王玉, 刘陪. 智能交通混合动态路径优化算法[J]. 吉林大学学报(工学版), 2018, 48(4): 1214-1223.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed