一种生成新坐标系的普适三点模型及其应用

doi:10.13229/j.cnki.jdxbgxb20181228

吉林大学学报(工学版) ›› 2020, Vol. 50 ›› Issue (1): 324-332.doi: 10.13229/j.cnki.jdxbgxb20181228

• 通信与控制工程 • 上一篇

一种生成新坐标系的普适三点模型及其应用

王凤艳¹(),严学新²,王明常¹,张旭晴¹,牛雪峰¹,王清³()

1. 吉林大学地球探测科学与技术学院, 长春 130026
2. 上海市地质调查研究院自然资源部地面沉降监测与防治重点实验室，上海 200072
3. 吉林大学建设工程学院, 长春 130026

收稿日期:2018-12-12 出版日期:2020-01-01 发布日期:2020-02-06
通讯作者: 王清 E-mail:wangfy@jlu.edu.cn;wangqing@jlu.edu.cn
作者简介:王凤艳（1970-），女，教授，博士. 研究方向：工程测量，相机标定.E-mail:wangfy@jlu.edu.cn
基金资助:
国家自然科学基金项目(41472243);自然资源部城市土地资源监测与仿真重点实验室开放基金项目(KF-2018-03-20);自然资源部地面沉降监测与防治重点实验室开放基金项目(KLLSMP201901)

Universal three-point model of generating a new coordinate system and its application

Feng-yan WANG¹(),Xue-xin YAN²,Ming-chang WANG¹,Xu-qing ZHANG¹,Xue-feng NIU¹,Qing WANG³()

1. College of Geo?Exploration Science and Technology, Jilin University, Changchun 130026, China
2. Key Laboratory of Land Subsidence Monitoring and Prevention, Ministry of Natural Resources，Shanghai Institute of Geological Survey, Shanghai 200072，China
3. College of Construction Engineering, Jilin University, Changchun 130026, China

Received:2018-12-12 Online:2020-01-01 Published:2020-02-06
Contact: Qing WANG E-mail:wangfy@jlu.edu.cn;wangqing@jlu.edu.cn

摘要/Abstract

摘要：

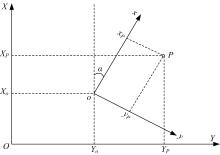
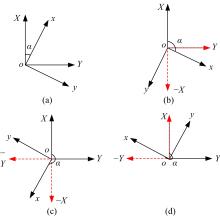
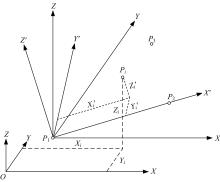
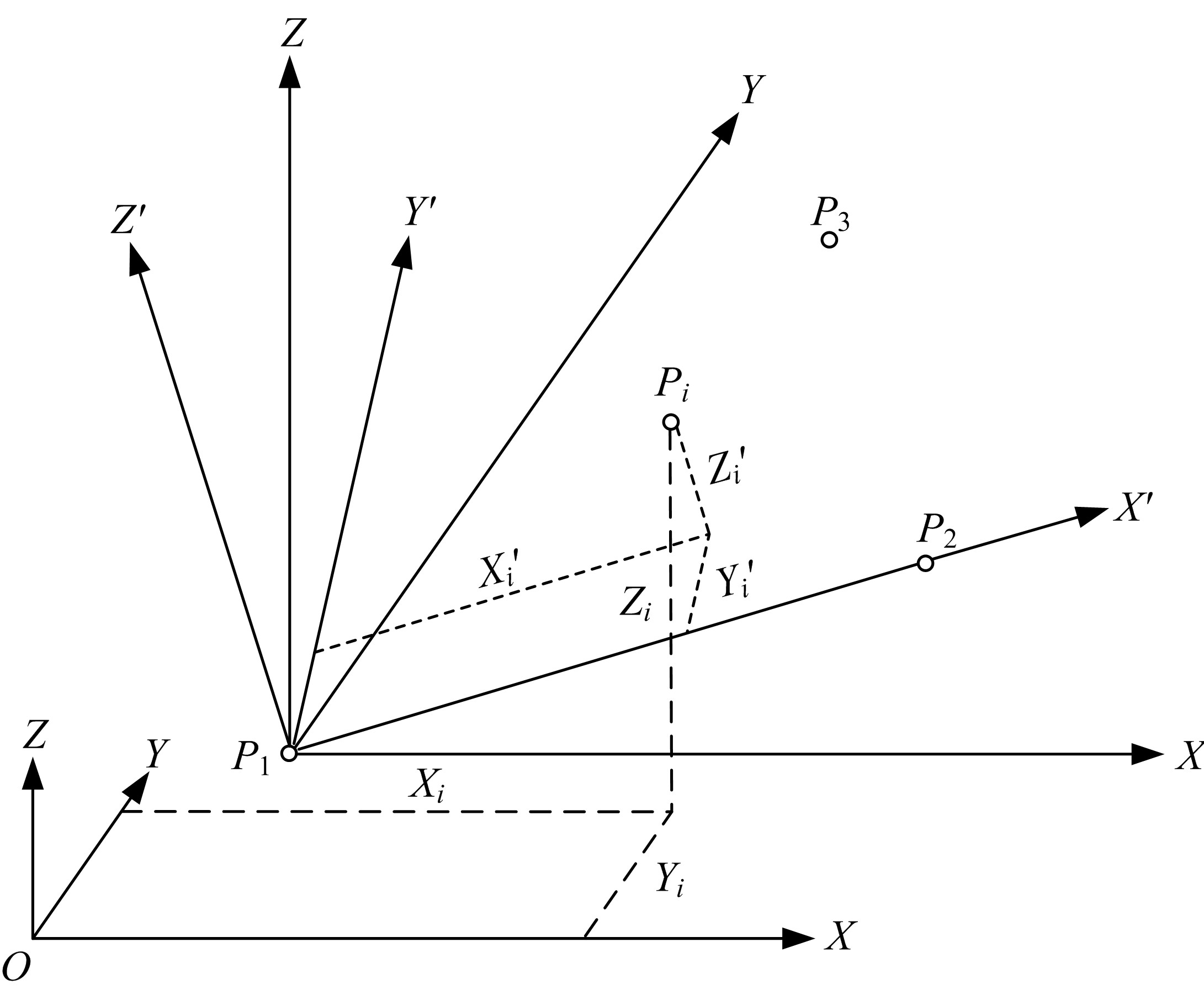
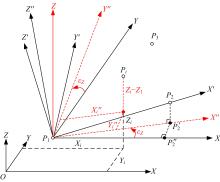
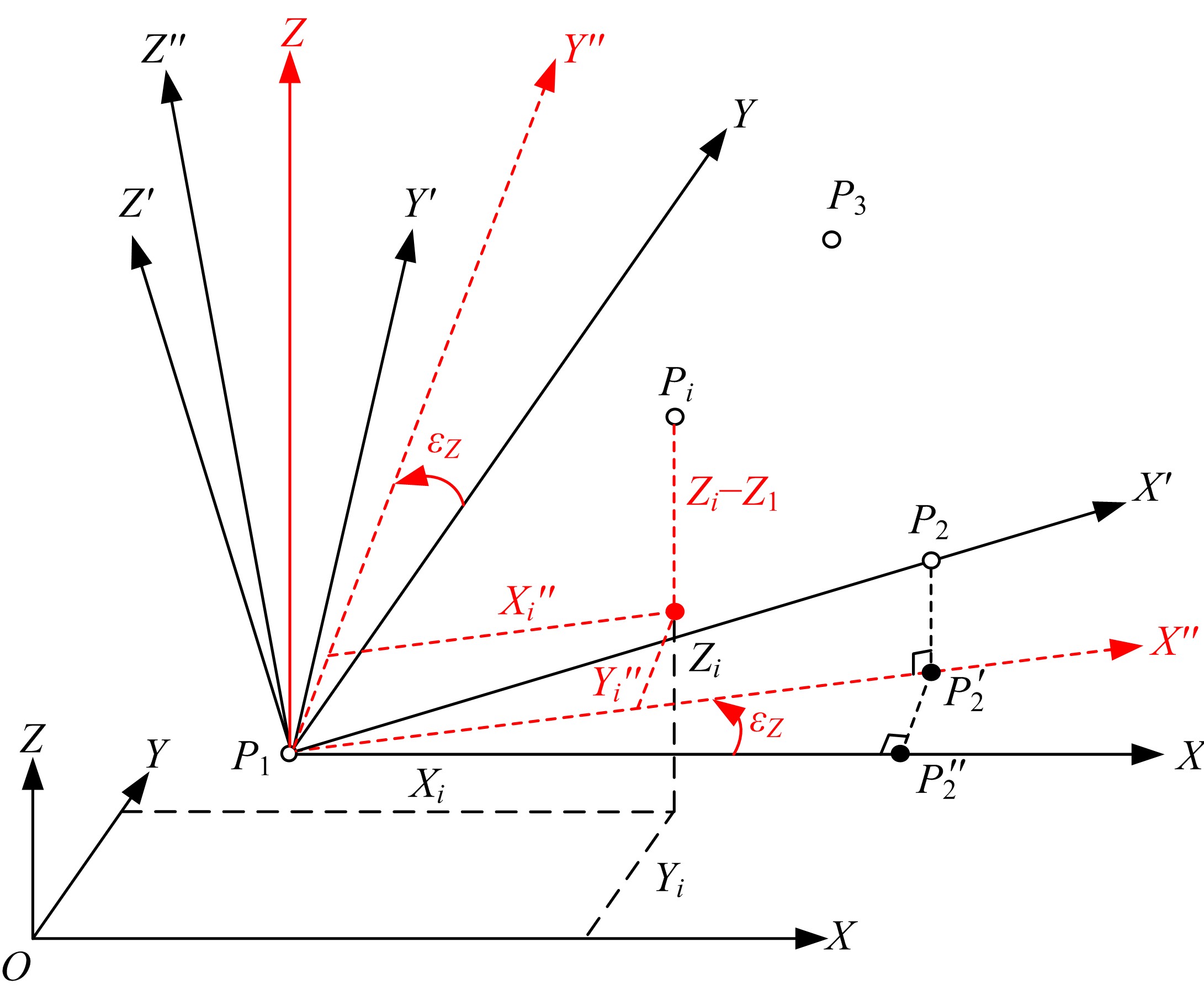
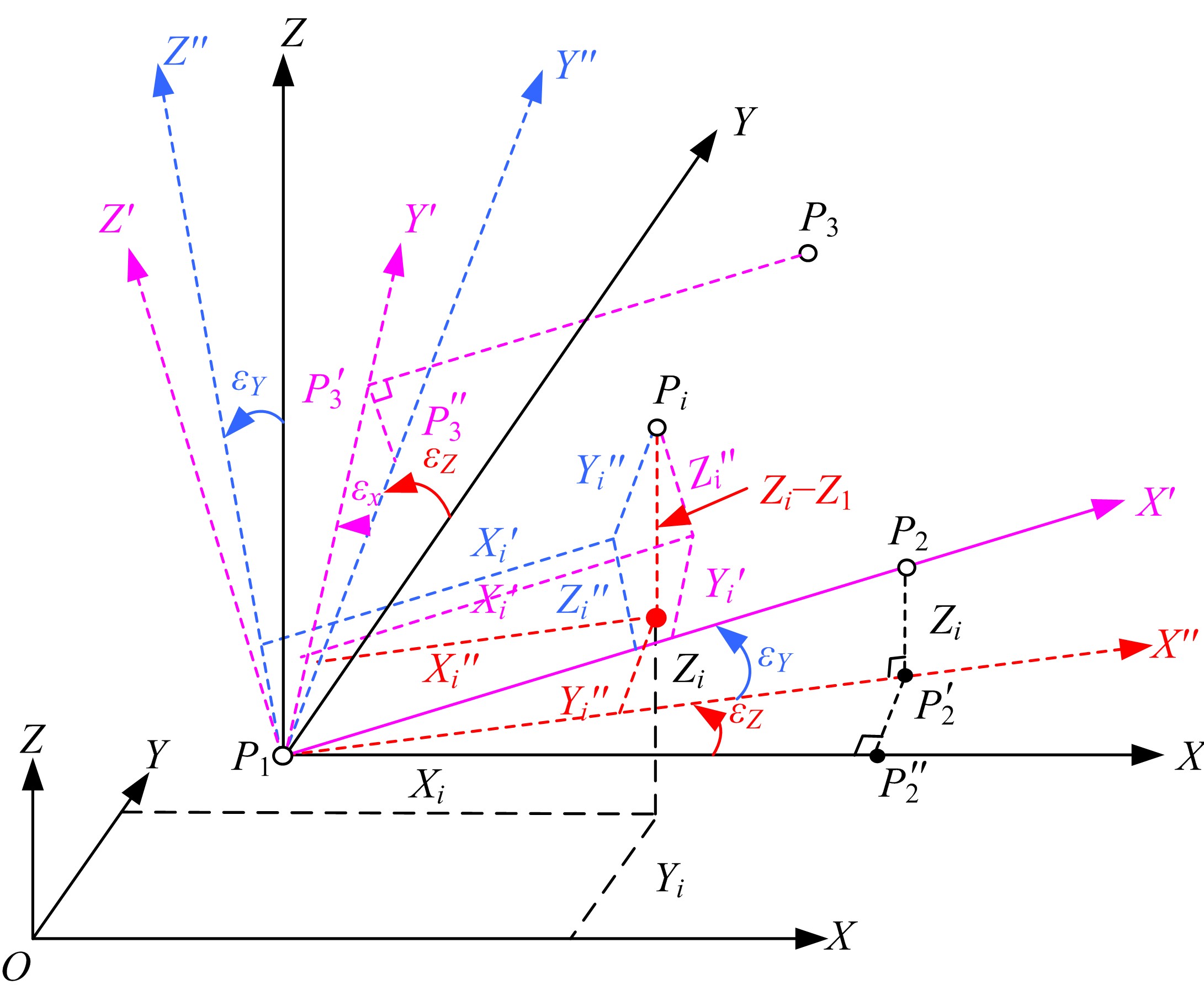
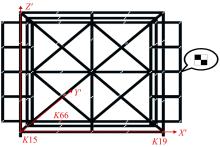
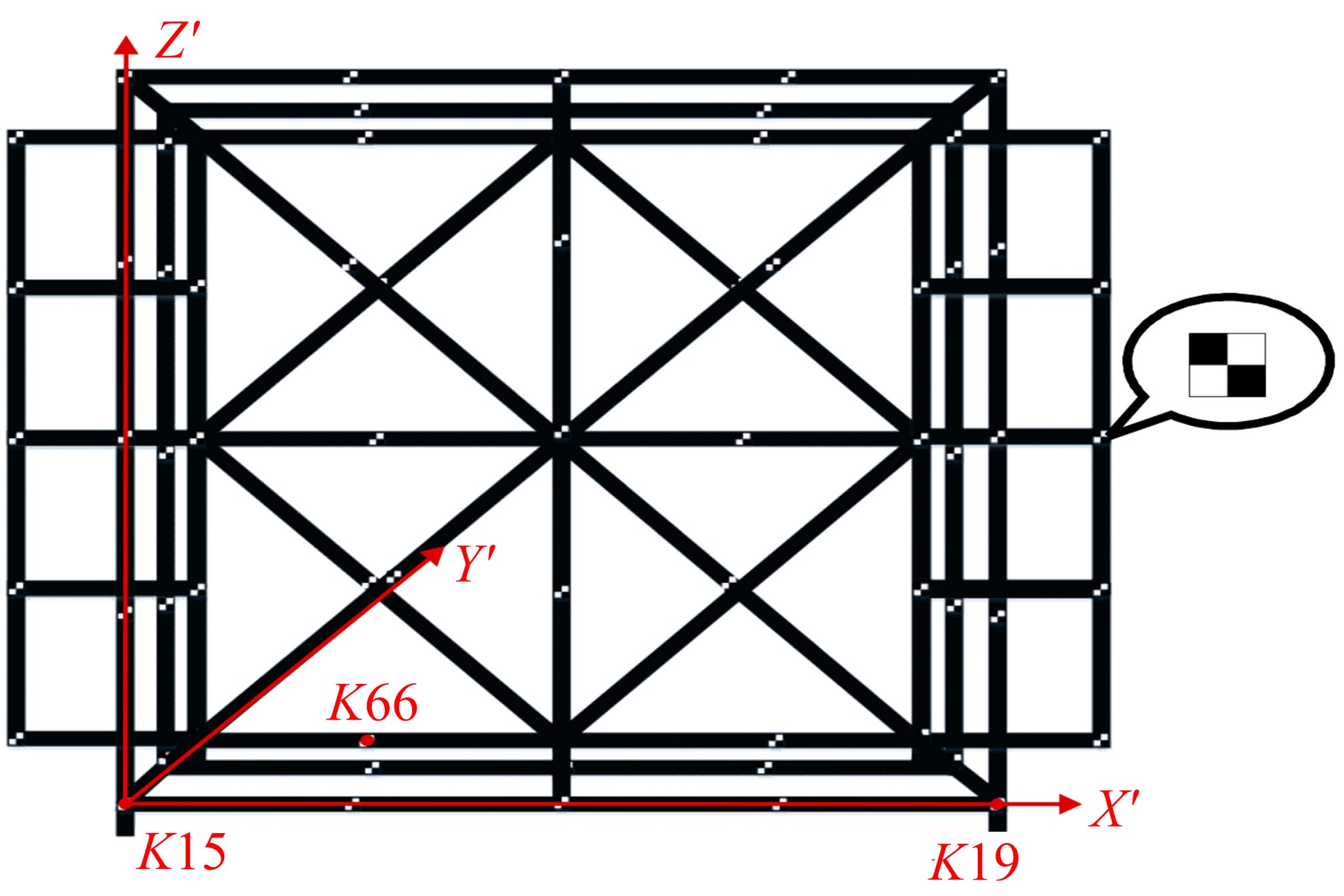
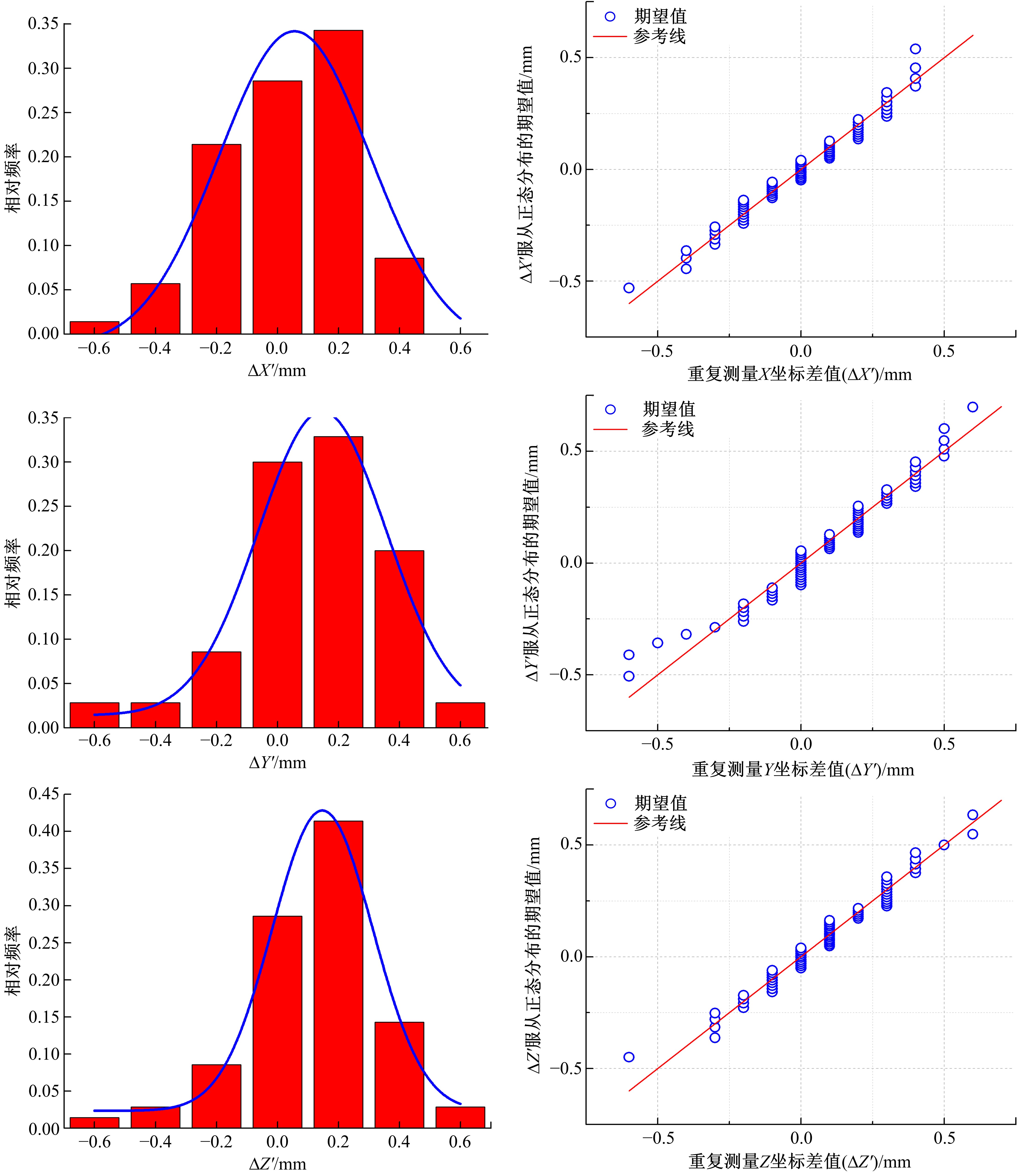
测量中经常涉及坐标系生成与转换问题，以左手系为例，推导了基于任意旋转角的平面直角坐标系顺时针变换模型，该模型也适用于右手系的逆时针变换，且旋转矩阵与旋转角大小无关，和坐标轴的顺序及旋转方向有关。在此基础上，针对工程与工业测量中的空间直角坐标系的生成与变换，提出了基于任意不共线三点生成新坐标系的普适模型，该模型通过在坐标逐步变换过程的旋转参数计算中加入详细判据，从而克服传统三点法生成新坐标系对三点的分布限制，用户可以按照任意需要生成新坐标系，并将该模型应用于非量测相机标定控制场的坐标系建立，验证了模型的可靠性。

关键词: 测量工程, 坐标系生成与转换, 普适三点模型, 轴对准, 相机标定控制场

Abstract:

Coordinate system generation and transformation play an important role in many fields. Taking the left-hand coordinate system as an example, a clockwise transformation model is deduced based on any rotation angle for plane rectangular coordinate systems in detail. The model is also suitable for the counterclockwise transformation for the right-hand coordinate system. The study shows that the form of rotation matrix has nothing to do with the size of rotation angle, but relates to the sequences and the rotation directions of coordinate axes, which changes when one of the two sequences changes, and stays the same when both sequences change. Based on the above derivation, a universal three-point model is proposed for the generation a new spatial rectangular coordinate system. By adding the fine criterions to the rotational parameter calculation in the gradual coordinate transformation, the universal model can arbitrarily generate a new coordinate system based on non-collinear three points and realize coordinate transformation. This model breaks the distribution limitations for three points used to generate a new coordinate system in the conventional axis alignment method. Furthermore, the universal model can be applied for generating the coordinate system of control field for the calibration of a non-metric camera which has been widely used in the fields of low-altitude remote sensing and close-range photogrammetry as a photoelectric sensor. The reliability of the proposed universal model is verified.

Key words: survey engineering, generation and transformation of coordinate system, universal three-point model, axis alignment, control field for camera calibration

中图分类号:

TP391

王凤艳,严学新,王明常,张旭晴,牛雪峰,王清. 一种生成新坐标系的普适三点模型及其应用[J]. 吉林大学学报(工学版), 2020, 50(1): 324-332.

Feng-yan WANG,Xue-xin YAN,Ming-chang WANG,Xu-qing ZHANG,Xue-feng NIU,Qing WANG. Universal three-point model of generating a new coordinate system and its application[J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(1): 324-332.

图/表 15

图1

图2

表1

不同轴序和旋转方向对应的旋转矩阵形式"

	顺时针	逆时针
左手系	$c o s α s i n α - s i n α c o s α$	$c o s α - s i n α s i n α c o s α$
右手系	$c o s α - s i n α s i n α c o s α$	$c o s α s i n α - s i n α c o s α$

表1

图3

图4

图5

图6

表2

图7

图8

图9

表3

表4

图10

表5

参考文献 22

1	Alashaikh A H. Numerical transformation technique for coordinate systems in the Kingdom of Saudi Arabia[J]. Arabian Journal of Geosciences, 2017, 10(6): 2903-2908.
2	朱振宇, 江国焰, 王永明. 工业测量系统自由坐标系建立方法研究[J]. 矿山测量, 2009(5): 63-69.
	Zhu Zhen-yu, Jiang Guo-yan, Wang Yong-ming. Study on the establishment of free-coordinate system of industrial measurement system[J]. Mine Surveying, 2009(5): 63-66, 69.
3	黄鹏, 王青, 李江雄, 等. 激光跟踪仪三维坐标转换综合优化方法[J]. 计算机集成制造系统, 2015, 21(11): 2912-2920.
	Huang Peng, Wang Qing, Li Jiang-xiong, et al. Comprehensive optimization for three-dimensional coordinate transformation of laser tracker[J]. Computer Integrated Manufacturing System, 2015, 21(11): 2912-2920.
4	Wang F, Wei X Z, and Li X. Coordinates transformation and the accuracy analysis in sensor network[J]. Journal of Systems Engineering and Electronics, 2005, 27(7): 1231-1234.
5	孔祥元, 郭际明. 控制测量学[M]. 武汉: 武汉大学出版社, 2006.
6	杨凡, 李广云, 王力. 三维坐标转换方法研究[J]. 测绘通报, 2010(6): 5-7, 15.
	Yang Fan, Li Guang-yun, Wang Li. Research on the methods of calculating 3D coordinate transformation parameters[J]. Bulletin of Surveying and Mapping, 2010(6): 5-7, 15.
7	曾文宪, 陶本藻. 三维坐标转换的非线性模型[J]. 武汉大学学报:信息科学版, 2003, 28(5): 566-568.
	Zeng Wen-xian, Tao Ben-zao. Non-linear adjustment model of three-dimensional coordinate transformation[J]. Geomatics and Information Science of Wuhan University, 2003, 28(5): 566-568.
8	潘国荣, 周莹, 张德海. 坐标转换模型在盾构姿态计算中的应用[J]. 大地测量与地球动力学, 2006, 26(3): 84-87.
	Pan Guo-rong, Zhou Ying, Zhang De-hai. 3D datum transformation model for determining orientation of shield in subway construction[J]. Journal of Geodesy and Geodynamics, 2006, 26(3): 84-87.
9	赵思齐. 用于沉管施工的实时定位系统开发及应用[D].上海:同济大学土木工程学院, 2007．
	Zhao Si-qi. Realtime positioning system in surveying of immersed tube[D]. Shanghai: College of Civil Engineering，Tongji University, 2007.
10	张凯, 单甘霖, 陈海, 等. 基于几何解算的飞机三维姿态测量方法[J]. 火力与指挥控制, 2012, 37(7): 43-46.
	Zhang Kai, Shan Gan-lin, Chen Hai, et al. Measurement of aircraft’s 3D pose based on geometric algorithms[J]. Fire Control & Command Control, 2012, 37(7): 43-46.
11	刘志平, 杨磊. 大旋转角的空间直角坐标转换方法的改进[J]. 大地测量与地球动力学, 2016, 36(7): 586-590.
	Liu Zhi-ping, Yang Lei. An improved method for spatial rectangular coordinate transformation with big rotation angle[J]. Journal of Geodesy and Geodynamics, 2016, 36(7): 586-590.
12	潘国荣, 汪大超, 周跃寅. 两种大转角空间坐标转换模型研究[J]. 山东科技大学学报:自然科学版, 2015, 34(1): 61-67.
	Pan Guo-rong, Wang Da-chao, Zhou Yue-yin. Two spatial coordinate transformation model of large angle[J]. Journal of Shandong University of Science and Technology (Natural Science), 2015, 34(1): 61-67.
13	陈义, 沈云中, 刘大杰. 适用于大旋转角的三维基准转换的一种简便模型[J]. 武汉大学学报:信息科学版, 2004, 29(12): 1101-1105.
	Chen Yi, Shen Yun-zhong, Liu Da-jie. A simplified model of three dimensional-datum transformation adapted to big rotation angle[J]. Geomatics and Information Science of Wuhan University, 2004, 29(12): 1101-1105.
14	Wu Y, Liu J, and Ge H Y. Comparison of total least squares and least squares for four-and seven-parameter model coordinate transformation[J]. Journal of Applied Geodesy, 2016, 10(4): 259-266.
15	李新友, 陈五一. 基于奇异值分解的刚体位姿误差检测方法[J]. 计算机集成制造系统, 2011, 17(9): 1981-1987.
	Li Xin-you, Chen Wu-yi. Detection of pose errors for a rigid body based on singular value decomposition method[J]. Computer Integrated Manufacturing Systems, 2011, 17(9): 1981-1987.
16	叶锃锋, 冯恩信. 基于四元数和卡尔曼滤波的两轮车姿态稳定方法[J]. 传感器学报, 2012, 25(4): 524-528.
	Ye Zeng-feng, Feng En-xin. Attitude stabilization based on quaternion and Kalman filter for two-wheeled vehicle[J]. Chinese Journal of Sensors and Actuators, 2012, 25(4): 524-528.
17	姚吉利, 韩保民, 杨元喜. 罗德里格矩阵在三维坐标转换严密解算中的应用[J]. 武汉大学学报:信息科学版, 2006, 31(12): 1094-1096, 1119.
	Yao Ji-li, Han Bao-min, Yang Yuan-xi. Applications of Rodrigue matrix in 3D coordinate transformation[J]. Geomatics and Information Science of Wuhan University, 2006, 31(12): 1094-1096, 1119.
18	张正禄. 工程测量学[M]. 武汉:武汉大学出版社, 2005.
19	冯文灏. 工业测量中标准尺的几种应用[J]. 测绘通报, 2003(3): 40-43.
	Feng Wen-hao. Some applications of standard rulers in industrial surveying[J]. Bulletin of Surveying and Mapping, 2003(3): 40-43.
20	武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉：武汉大学出版社, 2011.
21	王凤艳, 黄润秋, 陈剑平, 等. 基于计算机视觉和测量平差理论的相机标定[J]. 吉林大学学报:工学版, 2017, 47(3): 944-951.
	Wang Feng-yan, Huang Run-qiu, Chen Jian-ping, et al. Camera calibration based on computer vision and surveying adjustment fundamentals[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(3): 944-951.
22	吉林大学. 数码相机标定及影像校正系统Camera Calibration 1.0[P]. 中国: 2012SR039020, 2012-03-09.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

P₁		P₂		P₃		P₁	P₂	P₃
原点	X₁,Y₁,Z₁	卦限	X₂,Y₂,Z₂	卦限	X₃,Y₃,Z₃	X₁′,Y₁′,Z₁′	X₂′,Y₂′,Z₂′	X₃′,Y₃′,Z₃′
原点	0,0,0	1st	2,2,2	1st	1,3,1	0,0,0	3.464,0,0	2.8868,1.6330,0
				2nd	-4,1,1			-1.155,4.082,0
				3rd	-2,-4,2			-2.309,-4.32,0
				4th	2,-2,1			0.5774,-2.9439,0
				5th	1,3,-1			1.7321,2.8284,0
				6th	-4,1,-1			-2.3094,3.559,0
				7th	-2,-4,-2			-4.6188,-1.633,0
				8th	2,-2,-1			-0.5774,-2.9439,0
		2nd	-2,2,2	1st	1,3,1	0,0,0	3.464,0,0	1.7321，-2.8284,0
				2nd	-4,1,1			3.4641,2.4495,0
				3rd	-2,-4,2			0,4.8890,0
				4th	2,-2,1			-1.7321，-2.4495,0
				5th	1,3,-1			0.5774，-3.2660,0
				6th	-4,1,-1			2.3094,3.5590,0
				7th	-2,-4,-2			-2.3094,4.3205,0
				8th	2,-2,-1			-2.8868，-0.8165,0

点号	坐标（测量坐标系）			坐标（控制场坐标系）
点号	X/m	Y/m	Z/m	X′/m	Y′/m	Z′/m
K₁₅	0.1236	3.6481	-1.3054	0	0	0
K₁₉	1.6659	3.9391	-1.3079	1.5695	0	0
K₆₆	0.2381	4.8546	-1.3025	0.3363	1.1644	0
…	…	…	…	…	…	…
K₇₀	1.8394	5.1672	-1.3001	1.9678	1.1746	0.0005

点号	第1次测量坐标(控制场坐标系)				第2次测量坐标(控制场坐标系)			坐标差值
点号	X′/m	Y′/m		Z′/m	X′/m	Y′/m	Z′/m	ΔX′/m	ΔY′/mm	ΔZ′/mm
K₁	-0.0063	-0.0139	1.5655		-0.0065	-0.0136	1.5653	0.2	-0.3	0.2
K₂	0.4023	-0.0136	1.5676		0.4021	-0.0136	1.5673	0.2	0	0.3
K₃	0.7781	-0.0131	1.5697		0.7779	-0.0134	1.5694	0.2	0.3	0.3
K₄	1.1666	-0.0128	1.5714		1.1663	-0.0129	1.5712	0.3	0.1	0.2
K₅	1.5598	-0.0138	1.5717		1.5594	-0.014	1.5715	0.4	0.2	0.2
…	…	…	…		…	…	…	…	…	…
K₇₀	1.9679	1.175	0.0049		1.9678	1.1746	0.005	0.1	0.4	-0.1

相机参数		标定结果
主距	f_x/mm	24.4390±0.002
主距	f_y/mm	24.4416±0.002
主点偏移	c_x/mm	-0.1115±0.004
主点偏移	c_y/mm	0.1545±0.003
畸变系数	k₁	-1.7786E-04±6.9234E-07
	k₂	2.9316E-07±4.8850E-09
	p₁	-1.4317E-05±1.3790E-06
	p₂	2.0670E-06±1.4964E-07

[1]	王铁君,王维兰. 基于本体的唐卡图像标注方法[J]. 吉林大学学报(工学版), 2020, 50(1): 289-296.
[2]	王晓辉,吴禄慎,陈华伟. 基于法向量距离分类的散乱点云数据去噪[J]. 吉林大学学报(工学版), 2020, 50(1): 278-288.
[3]	王洪雁,邱贺磊,郑佳,裴炳南. 光照变化下基于低秩稀疏表示的视觉跟踪方法[J]. 吉林大学学报(工学版), 2020, 50(1): 268-277.
[4]	李雄飞,王婧,张小利,范铁虎. 基于SVM和窗口梯度的多焦距图像融合方法[J]. 吉林大学学报(工学版), 2020, 50(1): 227-236.
[5]	车翔玖,刘华罗,邵庆彬. 基于Fast RCNN改进的布匹瑕疵识别算法[J]. 吉林大学学报(工学版), 2019, 49(6): 2038-2044.
[6]	赵宏伟,王鹏,范丽丽,胡黄水,刘萍萍. 相似性保持实例检索方法[J]. 吉林大学学报(工学版), 2019, 49(6): 2045-2050.
[7]	周炳海,吴琼. 考虑工具和空间约束的机器人装配线平衡优化[J]. 吉林大学学报(工学版), 2019, 49(6): 2069-2075.
[8]	赵宏伟,李明昭,刘静,胡黄水,王丹,臧雪柏. 基于自然性和视觉特征通道的场景分类[J]. 吉林大学学报(工学版), 2019, 49(5): 1668-1675.
[9]	李宾,周旭,梅芳,潘帅宁. 基于K-means和矩阵分解的位置推荐算法[J]. 吉林大学学报(工学版), 2019, 49(5): 1653-1660.
[10]	孙延君,申铉京,陈海鹏,赵永哲. 基于局部平面线性点的翻拍图像鉴别算法[J]. 吉林大学学报(工学版), 2019, 49(4): 1320-1328.
[11]	李雄飞,宋璐,张小利. 基于协同经验小波变换的遥感图像融合[J]. 吉林大学学报(工学版), 2019, 49(4): 1307-1319.
[12]	翟凤文,党建武,王阳萍,金静,罗维薇. 基于扩展轮廓的快速仿射不变特征提取[J]. 吉林大学学报(工学版), 2019, 49(4): 1345-1356.
[13]	刘元宁,刘帅,朱晓冬,霍光,丁通,张阔,姜雪,郭书君,张齐贤. 基于决策粒子群优化与稳定纹理的虹膜二次识别[J]. 吉林大学学报(工学版), 2019, 49(4): 1329-1338.
[14]	李志慧,钟涛,赵永华,胡永利,李海涛,赵景伟. 面向车辆自主驾驶的行人跟踪算法[J]. 吉林大学学报(工学版), 2019, 49(3): 680-687.
[15]	欧阳丹彤,肖君,叶育鑫. 基于实体对弱约束的远监督关系抽取[J]. 吉林大学学报(工学版), 2019, 49(3): 912-919.

一种生成新坐标系的普适三点模型及其应用

Universal three-point model of generating a new coordinate system and its application

RICH HTML

PDF (PC)

摘要/Abstract

引用本文

使用本文

图/表 15

参考文献 22

相关文章 15

Metrics

本文评价

推荐阅读 0