吉林大学学报(工学版) ›› 2021, Vol. 51 ›› Issue (6): 1975-1981.doi: 10.13229/j.cnki.jdxbgxb20200613

• 车辆工程·机械工程 • 上一篇    

新型结构可靠性分析自适应加点策略

李国发1,2(),陈泽权1,2,何佳龙1,2()   

  1. 1.吉林大学 数控装备可靠性教育部重点实验室 长春 130022
    2.吉林大学 机械与航空航天工程学院 长春 130022
  • 收稿日期:2020-08-11 出版日期:2021-11-01 发布日期:2021-11-15
  • 通讯作者: 何佳龙 E-mail:ligf@jlu.edu.cn;hejl@jlu.edu.cn
  • 作者简介:李国发（1970-），男，教授，博士. 研究方向：数控装备可靠性理论及其全生命周期工程. E-mail：ligf@jlu.edu.cn
  • 基金资助:
    国家自然科学基金项目(51905209);吉林省中青年科技创新领军人才及团队项目(20190101015JH);吉林大学高层次科技创新团队项目（JLUSTIRT）

New adaptive sampling strategy for structural reliability analysis

Guo-fa LI1,2(),Ze-quan CHEN1,2,Jia-long HE1,2()   

  1. 1.Key Laboratory of CNC Equipment Reliability，Ministry of Education，Jilin University，Changchun 130022，China
    2.College of Mechanical and Aerospace Engineering，Jilin University，Changchun 130022，China
  • Received:2020-08-11 Online:2021-11-01 Published:2021-11-15
  • Contact: Jia-long HE E-mail:ligf@jlu.edu.cn;hejl@jlu.edu.cn

RICH HTML

 3   

PDF (PC)

209

摘要：

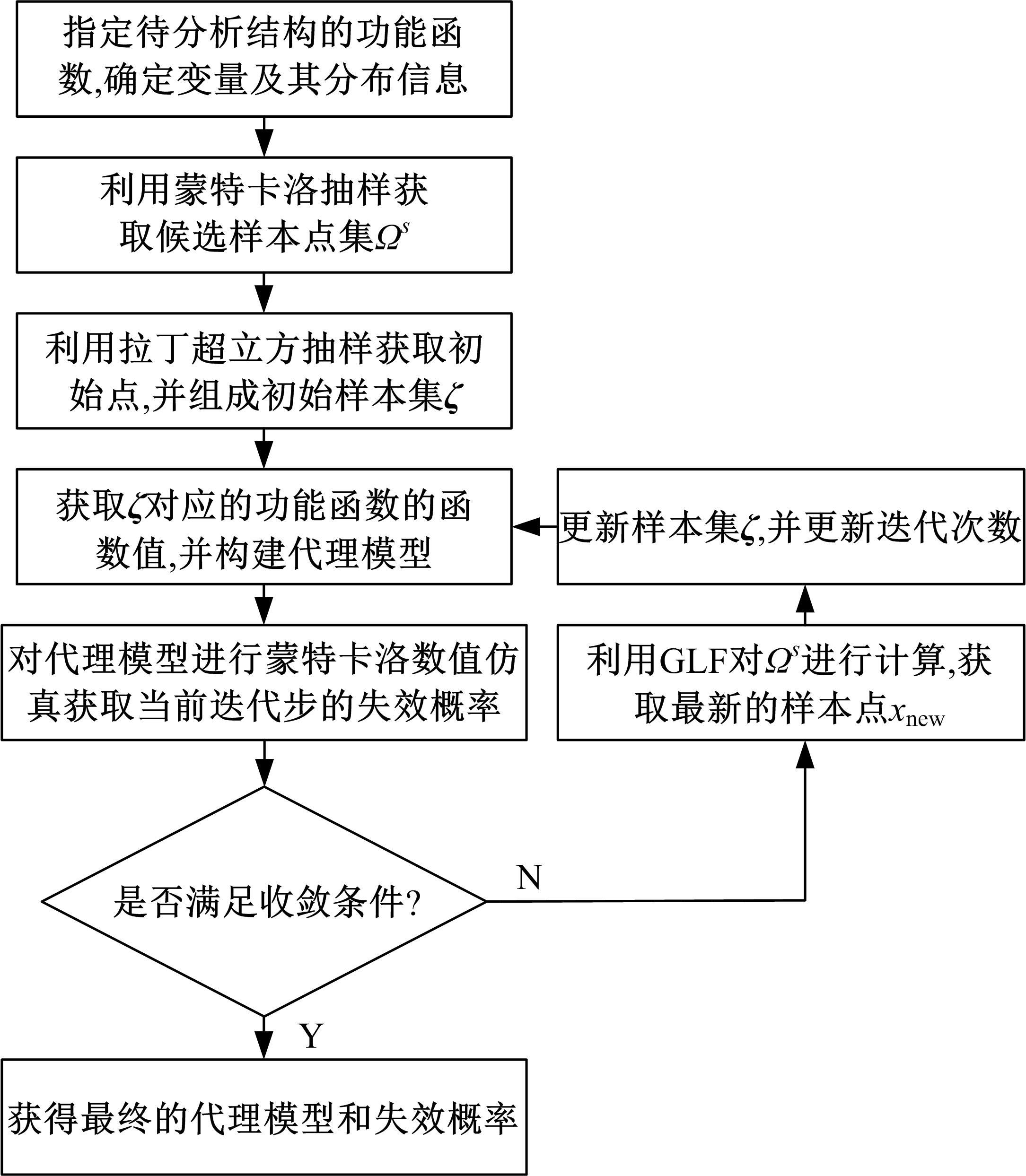
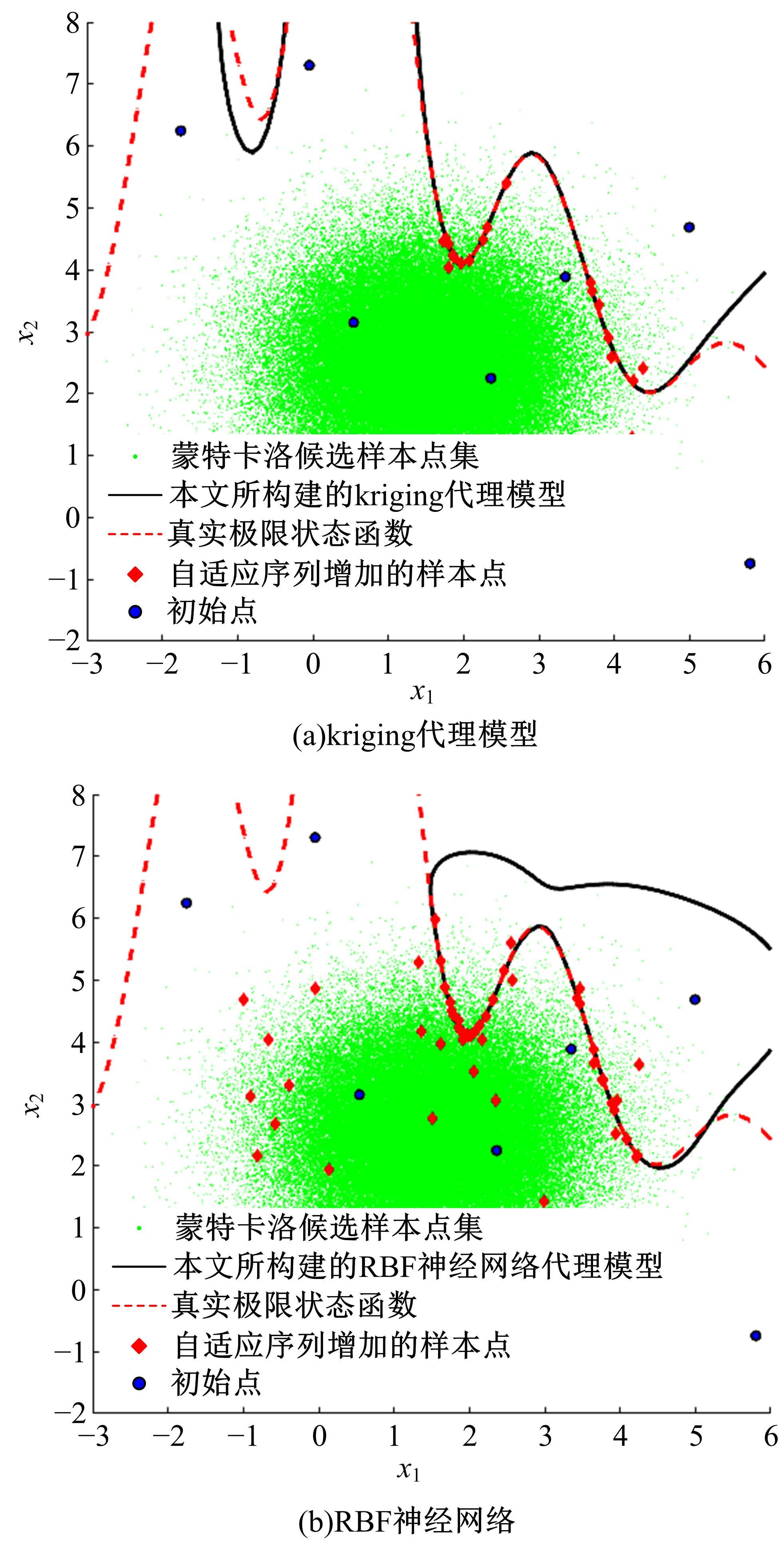
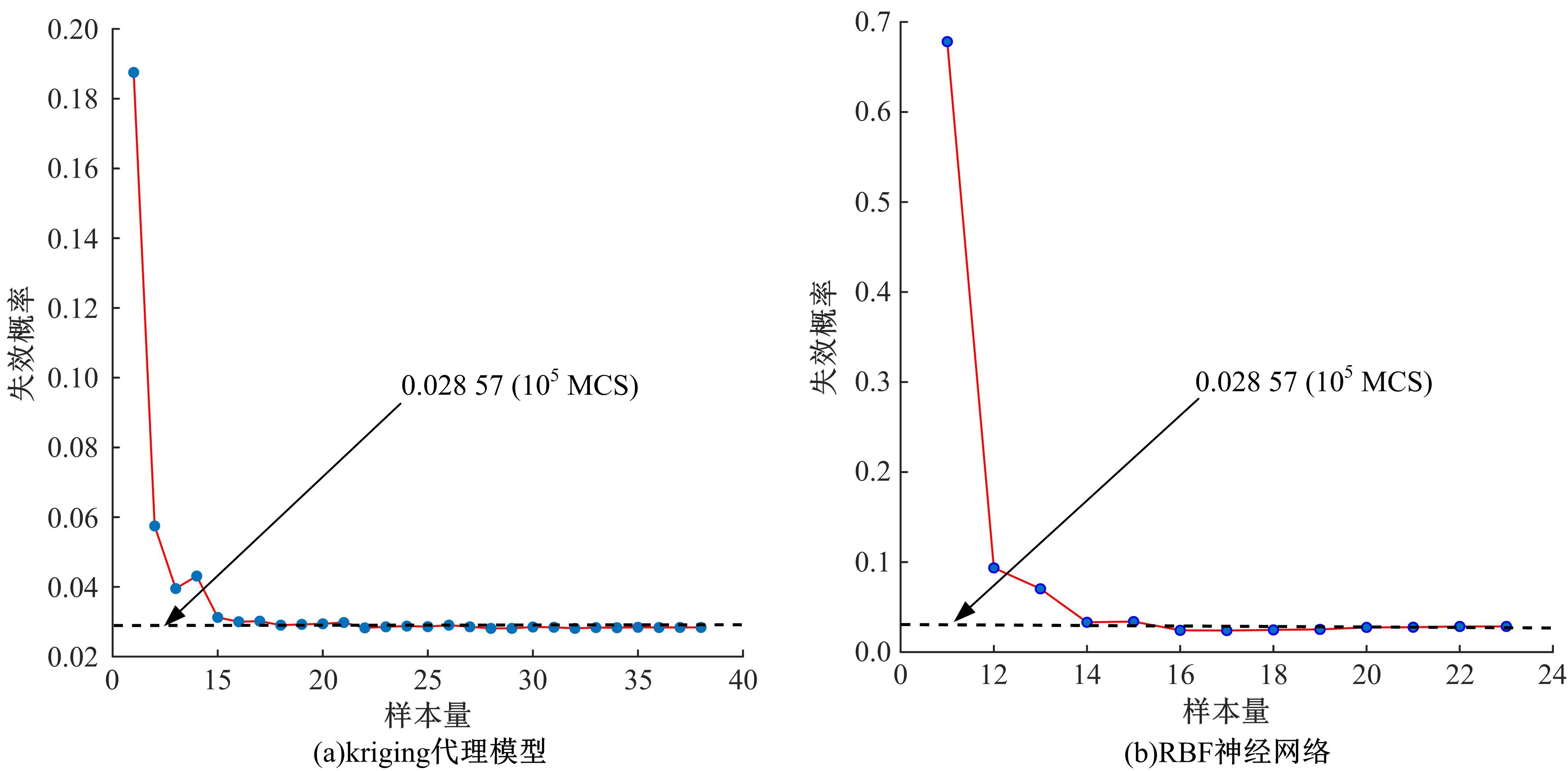
为了在进行结构可靠性分析时，能够构建高精度、高效率的代理模型，提出了一种面向多种代理模型的基于通用学习函数（GLF）的结构可靠性分析自适应加点策略。该策略被视为一个多目标优化过程，GLF考虑了样本点间的平均距离和最小距离、是否分布在极限状态函数的附近以及联合概率密度函数等因素，使得自适应添加的样本点能稳健、高效地提升代理模型对失效概率的估计精度。数值案例和工程案例结果表明，针对不同的代理模型，GLF能够利用少量的样本点，高精度、高效率地估计出结构的失效概率。

关键词: 结构可靠性, 可靠性分析, 代理模型, 自适应加点, 学习函数

Abstract:

In structural reliability analysis, choosing an appropriate adaptive sampling strategy is the key to constructing a high-precision and high-efficiency surrogate model. An adaptive sampling strategy for structural reliability analysis based on General Learning Function (GLF) for multiple surrogate models is proposed. The adaptive sampling strategy is regarded as a multi-objective optimization process, so the average and the minimum distance between the sample points, whether they are distributed near the limit state function, and the probability density function are all considered by the GLF to ensure that the new sample points can robustly and efficiently improve the surrogate model estimation accuracy of failure probability. Numerical cases and engineering case show that for different surrogate models, the GLF can use a small number of sample points to estimate the structural failure probability with high accuracy and efficiency.

Key words: structural reliability, reliability analysis, surrogate model, adaptive sampling, learning function

中图分类号: 

  • TB114.3

图1

自适应结构可靠性分析流程图"

图2

基于GLF的代理模型与真实极限状态函数的对比"

表1

本文方法指导的代理模型与MCS的对比"

分析方法代理模型样本量失效概率相对误差/%
MCS-1050.014 63-
本文方法kriging模型10+290.014 550.55
RBF神经网络10+560.014 690.41

图3

无阻尼单自由度振荡系统"

表2

变量的分布信息"

变量均值标准差分布类型
m10.05正态分布
c110.1正态分布
c20.10.01正态分布
r0.050.05正态分布
F110.2正态分布
t110.2正态分布

表3

本文方法指导的代理模型与MCS的对比"

分析方法代理模型样本量失效概率相对误差/%
MCS-1050.028 57-
本文方法kriging模型10+270.028 390.63
RBF神经网络10+130.028 540.11

图4

GLF学习函数指导的代理模型的失效概率收敛图"

1 Ghohani A H, Rashki M, Rostamian M, et al. Refined first-order reliability method using cross-entropy optimization method[J]. Engineering with Computers, 2019, 35(4):1507-1509.
2 Behrooz K, Subrata C. A hybrid self-adaptive conjugate first order reliability method for robust structural reliability analysis[J]. Applied Mathematical Modelling, 2018, 53: 319-332.
3 Lee C H, Kim Y. Probabilistic flaw assessment of a surface crack in a mooring chain using the first- and second-order reliability method[J]. Marine Structures, 2019, 63: 1-15.
4 Meng Z, Zhou H L, Hu H, et al. Enhanced sequential approximate programming using second order reliability method for accurate and efficient structural reliability-based design optimization[J]. Applied Mathematical Modelling, 2018, 62: 562-579.
5 Zhang X F, Wang L, Sørensen J D. REIF: a novel active-learning function toward adaptive Kriging surrogate models for structural reliability analysis[J]. Reliability Engineering & System Safety, 2019, 185: 440-454.
6 Marelli S, Sudret B. An active-learning algorithm that combines sparse polynomial chaos expansions and bootstrap for structural reliability analysis[J]. Structural Safety, 2018, 75: 67-74.
7 Xu J, Kong F. A cubature collocation based sparse polynomial chaos expansion for efficient structural reliability analysis[J]. Structural Safety, 2018, 74: 24-31.
8 孟广伟, 李广博, 周振平, 等. 基于Fourier正交基神经网络响应面法的结构可靠性分析[J]. 吉林大学学报:工学版, 2012, 42(): 135-138.
Meng Guang-wei, Li Guang-bo, Zhou Zhen-ping, et al.Structure reliability analysis based on Fourier orthogonal neural network response surface method[J]. Journal of Jilin University (Engineering and Technology Edition), 2012, 42(Sup.1):135-138.
9 Fan C B, Huang Y B, Wang Q F. Sparsity-promoting polynomial response surface: a new surrogate model for response prediction[J]. Advances in Engineering Software, 2014, 77: 48-65.
10 Rashki M, Azarkish H, Rostamian M, et al. Classification correction of polynomial response surface methods for accurate reliability estimation[J]. Structural Safety, 2019, 81: No.101869.
11 Roy A, Manna R, Chakraborty S. Support vector regression based metamodeling for structural reliability analysis[J]. Probabilistic Engineering Mechanics, 2019, 55:18-89.
12 Zhu C X, Zhao H B. Least square support vector machine for structural reliability analysis[J]. International Journal of Computer Applications in Technology, 2016, 53(1): 51-61.
13 Echard B, Gayton N, Lemaire M. AK-MCS: an active learning reliability method combining Kriging and Monte Carlo simulation[J]. Structural Safety, 2011, 33(2): 145-154.
14 Jiang C, Qiu H B, Gao L, et al. EEK-SYS: system reliability analysis through estimation error-guided adaptive Kriging approximation of multiple limit state surfaces[J]. Reliability Engineering & System Safety, 2020,198: No.106906.
15 Lv Z, Lu Z Z, Wang P. A new learning function for Kriging and its applications to solve reliability problems in engineering[J]. Computers & Mathematics with Applications, 2015, 70(5): 1182-1197.
16 Sun Z L, Wang J, Li R, et al. LIF: a new Kriging based learning function and its application to structural reliability analysis[J]. Reliability Engineering & System Safety, 2017, 157: 152-165.
17 Wang Z Y, Shafieezadeh A. REAK: reliability analysis through error rate-based adaptive kriging[J]. Reliability Engineering & System Safety, 2019, 182: 33-45.
18 Yang X F, Liu Y S, Mi C Y, et al. System reliability analysis through active learning Kriging model with truncated candidate region[J]. Reliability Engineering & System Safety, 2018, 169: 235-241.
19 Bichon B J, Eldred M S, Swiler L P, et al. Efficient global reliability analysis for nonlinear implicit performance functions[J]. Aiaa Journal, 2008, 46(10): 2459-2468.
20 肖宁聪,袁凯,王永山. 基于序列代理模型的结构可靠性分析方法[J]. 电子科技大学学报, 2019, 48(1): 156-160.
Xiao Ning-cong, Yuan Kai, Wang Yong-shan. Structural reliability analysis using sequential surrogate models[J]. Journal of University of Electronic Science and Technology of China, 2019, 48(1): 156-160.
[1] 杜尊令,张义民. 基于随机流量下柱塞泵的可靠性分析[J]. 吉林大学学报(工学版), 2021, 51(6): 1967-1974.
[2] 樊学平,杨光红,肖青凯,刘月飞. 大跨桥梁主梁失效概率分析的最优R-Vine Copula[J]. 吉林大学学报(工学版), 2021, 51(4): 1296-1305.
[3] 于向军,槐元辉,李学飞,王德武,俞安. 基于克里金和粒子群算法的装载机铲掘轨迹规划[J]. 吉林大学学报(工学版), 2020, 50(2): 437-444.
[4] 刘颖, 张凯, 于向军. 基于代理模型的中空轴式大型静压轴承多目标优化[J]. 吉林大学学报(工学版), 2017, 47(4): 1130-1137.
[5] 孟广伟, 冯昕宇, 周立明, 李锋. 基于降维算法的结构可靠性分析[J]. 吉林大学学报(工学版), 2017, 47(1): 174-179.
[6] 周志国, 卢江跃. 弯曲振动下压电陶瓷复合圆盘的可靠性分析[J]. 吉林大学学报(工学版), 2013, 43(增刊1): 138-142.
[7] 姜封国, 赵景鲁. 受火后钢筋混凝土构件的可靠性[J]. 吉林大学学报(工学版), 2013, 43(06): 1500-1503.
[8] 王晓燕, 申桂香, 张英芝, 郑珊, 牛序磊, 梁栋. 基于DEMATEL方法的数控装备故障相关性分析[J]. 吉林大学学报(工学版), 2012, 42(增刊1): 100-103.
[9] 孟广伟, 李广博, 周振平, 周立明. 基于Fourier正交基神经网络响应面法的结构可靠性分析[J]. 吉林大学学报(工学版), 2012, 42(增刊1): 135-138.
[10] 张英芝1,郑锐2,申桂香1,王志琼1,李怀洋1,郑珊1. 基于Copula理论的数控装备故障相关性[J]. 吉林大学学报(工学版), 2011, 41(6): 1636-1640.
[11] 李艺，闫运起，赵文 . 现役结构增层刚度时变可靠性分析[J]. 吉林大学学报(工学版), 2009, 39(02): 398-0401.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
版权所有 © 《吉林大学学报(工学版)》编辑部
地址：长春市人民大街5988号　电话：+86-431-85095297　传真：+86-431-85094074　E-mail: xbgxb@jlu.edu.cn
本系统由北京玛格泰克科技发展有限公司设计开发