基于Gamma过程的加速退化试验多目标优化设计

doi:10.13229/j.cnki.jdxbgxb20211100

吉林大学学报(工学版) ›› 2022, Vol. 52 ›› Issue (2): 361-367.doi: 10.13229/j.cnki.jdxbgxb20211100

• 车辆工程·机械工程 • 上一篇

基于Gamma过程的加速退化试验多目标优化设计

张立杰^1,^2,³(),阿喜塔^1,²,田笑^1,²,李稳^1,^2,³()

^1.燕山大学先进锻压成形技术与科学教育部重点实验室，河北秦皇岛 066004
^2.燕山大学河北省重型机械流体动力传输与控制重点实验室，河北秦皇岛 066004
^3.高端工程机械智能制造国家重点实验室，江苏徐州 221004

收稿日期:2021-10-23 出版日期:2022-02-01 发布日期:2022-02-17
通讯作者: 李稳 E-mail:ljzhang@ysu.edu.cn;liwen9933@126.com
作者简介:张立杰（1969-），男，教授，博士.研究方向：液压测控技术，机器人技术.E-mail：ljzhang@ysu.edu.cn
基金资助:
国家自然科学基金项目(51875499)

Multi⁃objective optimization design of accelerated degradation test based on Gamma process

Li-jie ZHANG^1,^2,³(),Xi-ta A^1,²,Xiao TIAN^1,²,Wen LI^1,^2,³()

^1.Key Laboratory of Advanced Forging & Stamping Technology and Science，Ministry of Education of China，Yanshan University，Qinhuangdao 066004，China
^2.Hebei Key Laboratory of Heavy Machinery Fluid Power Transmission and Control，Yanshan University，Qinhuangdao 066004，China
^3.State Key Laboratory of Intelligent Manufacturing of Advanced Construction Machinery，Xuzhou 221004，China

Received:2021-10-23 Online:2022-02-01 Published:2022-02-17
Contact: Wen LI E-mail:ljzhang@ysu.edu.cn;liwen9933@126.com

摘要/Abstract

摘要：

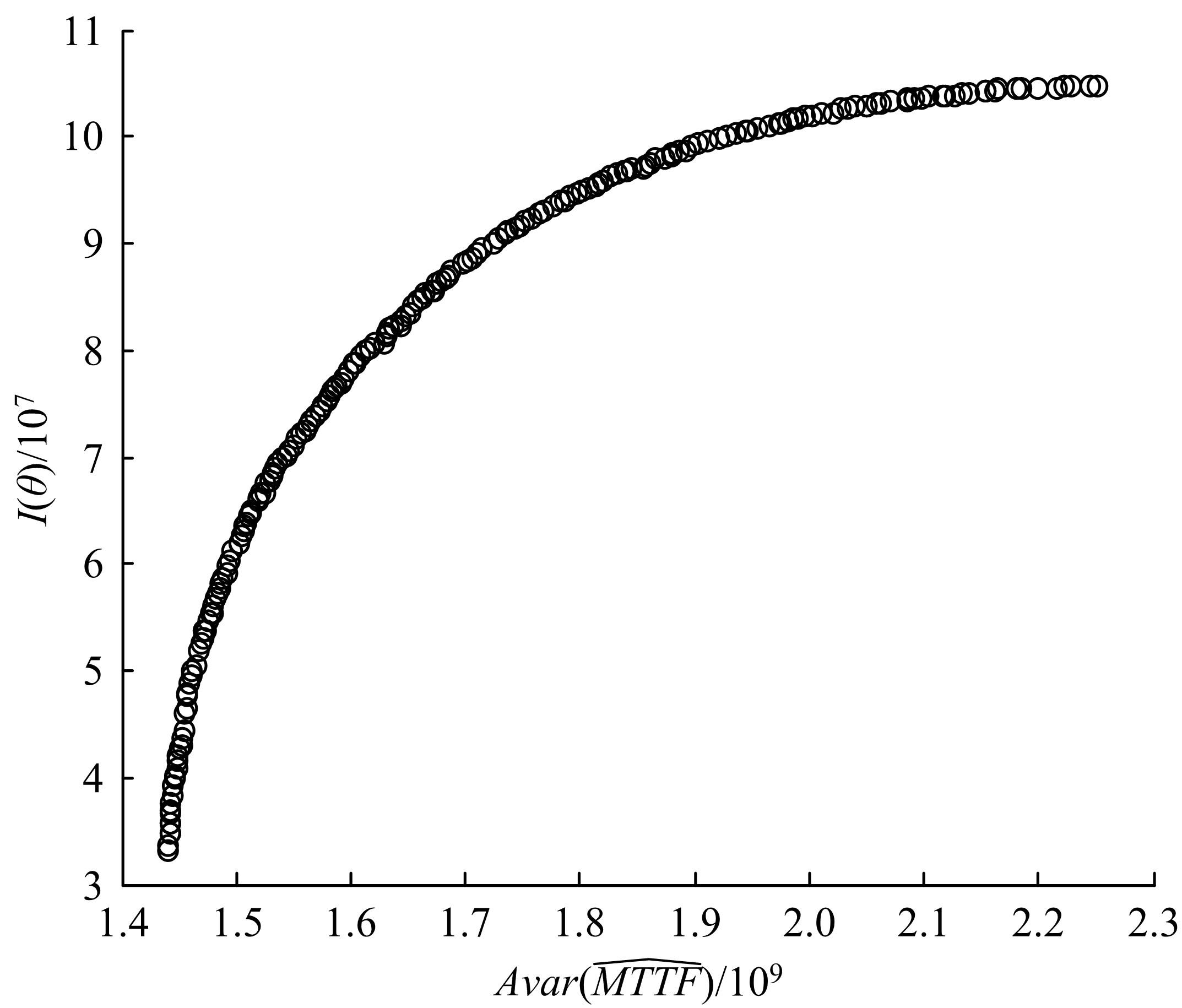
为得到加速退化试验优化设计中兼顾多个优化目标的相对最优试验配置，提出一种恒定应力加速退化试验多目标优化设计方法。基于Gamma过程建立了加速退化模型，通过极大似然估计方法求解未知参数。综合考虑模型拟合精度及寿命估计精度构建了多目标优化模型，通过NSGA-II对模型进行求解，建立兼顾多个优化目标的Pareto前沿集。以单目标优化目标函数值为基准，计算Pareto前沿集中的各目标函数相对比重。在此基础上，采用层次分析法对拟进行的加速退化试验进行专家决策，得出各目标函数的权重。以目标函数相对比重与目标函数权重误差最小为评价标准，选出Pareto前沿集中的相对最优试验配置。最后，以碳膜电阻的加速退化试验数据为实例验证了本文方法的有效性。

关键词: 加速退化试验, 多目标优化设计, Gamma过程, 层次分析法

Abstract:

In order to obtain the relative optimal test configuration considering multiple optimization objectives in the optimization design of accelerated degradation test， a multi-objective optimization design method of constant stress accelerated degradation test is proposed. The accelerated degradation model is established based on gamma process， and the unknown parameters are solved by maximum likelihood estimation method. Considering the model fitting accuracy and life estimation accuracy， a multi-objective optimization model is constructed. The model is solved by NSGA-II， and a Pareto frontier set considering multiple optimization objectives is established. The relative proportion of each objective function in Pareto frontier set is calculated based on the value of single objective optimization objective function. On this basis， the Analytic Hierarchy Process is used to make expert decision on the accelerated degradation test to be carried out， and the weight value of each objective function is obtained. Taking the minimum error between the relative proportion of the objective function and the weight value of the objective function as the evaluation standard， the relatively optimal test configuration in the Pareto front set is selected. Finally， the effectiveness of the proposed method is verified by the accelerated degradation test data of carbon film resistance.

Key words: accelerated degradation test, multi-objective optimization design, Gamma process, analytic hierarchy process

中图分类号:

TB114.3

张立杰,阿喜塔,田笑,李稳. 基于Gamma过程的加速退化试验多目标优化设计[J]. 吉林大学学报(工学版), 2022, 52(2): 361-367.

Li-jie ZHANG,Xi-ta A,Xiao TIAN,Wen LI. Multi⁃objective optimization design of accelerated degradation test based on Gamma process[J]. Journal of Jilin University(Engineering and Technology Edition), 2022, 52(2): 361-367.

图/表 4

图1

表1

CSADT单目标优化设计结果"

目标函数	n₁	n₂	n₃	S₁	S₂	S₃	函数值
I（θ）	11	15	4	50	200	119	1.03×10⁸
$A v a r (M T T F ?)$	14	3	13	90	200	91	1.44×10⁹

表1

表2

表3

参考文献 23

1	Hao H, Su C, Li C. LED lighting system reliability modeling and inference via random effects gamma process and copula function[J]. International Journal of Photoenergy, 2015(1): 1-8.
2	张建平, 张蓓. 基于三参数威布尔函数法的光电器件寿命快速评估模型及其应用[J]. 电子元件与材料, 2021, 40(2): 137-143.
	Zhang Jian-ping, Zhang Bei. Rapid life assessment model of optoelectronic devices based on threeparameter weibull function method and its applications[J]. Electronic Components and Materials, 2021, 40(2): 137-143.
3	Sun L, Wang X, Zhang G, et al. Life assessment of organic coating based on accelerated de-gradation test and modeling[C]∥IEEE Interaional Conference on Industrial Engineering and Engineering Management, Singapore, 2015: 1644-1647.
4	Han D, Ng H. Comparison between constant-stress and step-stress accelerated life tests undertime constraint[J]. Naval Research Logistics, 2013, 60(7): 541-556.
5	Ge Z, Li X, Jiang T, et al. Optimal design forstep-stress accelerated degradation testing based on D-optimality[C]∥Reliability & Maintainability Symposium IEEE, Lake Buena Vista, 2011: 1-6.
6	Omshi E M, Shemehsavar S. Optimal design for accelerated degradation test based on D-optimality[J]. Iranian Journal of Science and Technology Transactions A Science, 2019, 43(4): 1811-1818.
7	Hu C, Lee M Y, Tang J. Optimum step-stress accelerated degradation test for wiener degradation process under constraints[J]. European Journal of Operational Research, 2015, 241(2): 412-421.
8	Si S, Zhai G F, Zheng B K, et al. Optimal design of accelerated degradation failure mechanism consistency discriminant test based on d-optimality[C]∥International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, Harbin, 2019: 967-972.
9	Tseng S T, Balakrishnan N, Tsai C C. Optimal step-stress accelerated degradation test plan for gamma degradation processes[J]. IEEE Transactions on Reliability, 2009, 58(4): 611-618.
10	Tsai C, Tseng S, Balakrishnan N. Optimal design for degradation tests based on gamma processes with random effects[J]. IEEE Transactions on Reliability, 2012, 61(2): 604-613.
11	Lim H, Yum B J. Optimal design of accelerated degradation tests based on wiener process models[J]. Journal of Applied Statistics, 2011, 38(2): 309-325.
12	Li X, Hu Y, Zhou J, et al. Bayesian step stress accelerated degradation testing design: amulti-objective pareto-optimal approach[J]. Reliability Engineering & System Safety, 2018, 171: 9-17.
13	Wang H, Zhao Y, Ma H B, et al. Optimal design of constant-stress accelerated degradation tests using the M-optimality criterion[J]. Reliability Engineering & System Safety, 2017, 164: 45-54.
14	Wu Z, Liu X, Guo B, et al. Multi-objective optimization design of constant stress accelerated degradation test using inverse gaussian process[J]. IEEE Access, 2019, 7: 28757-28768.
15	Saaty T L. The Analytic Hierarchy Process[M]. New York: McGraw-Hill International, 1980.
16	郑玉彬, 杨斌, 王晓峰, 等. 基于威布尔分布的电主轴加速寿命试验时间设计[J]. 吉林大学学报: 工学版, 2018, 48(3): 767-772.
	Zheng Yu-bin, Yang Bin, Wang Xiao-feng, et al. Reliability evaluation model of tool competitive failure[J]. Journal of Jilin University(Engineering and Technology Edition), 2018, 48(3): 767-772.
17	李常有, 徐敏强, 郭耸, 等. 基于gamma过程及贝叶斯估计的实时可靠性评估[J]. 宇航学报, 2009, 30(4): 1722-1726.
	Li Chang-you, Xu Min-Qiang, Guo Song, et al. Real time reliability evaluation based on gamma process and bayesian estimation[J]. Journal of Astronautics, 2009, 30(4): 1722-1726.
18	Sun B, Yan M C, Feng Q, et al. Gamma degradation process and accelerated model combined reliability analysis method for rubber O-rings[J]. IEEE Access, 2018, 6: 10581-10590.
19	唐圣金, 郭晓松, 周召发, 等. 步进应力加速退化试验的建模与剩余寿命估计[J]. 机械工程学报, 2014, 50(16): 33-40.
	Tang Sheng-jin, Guo Xiao-song, Zhou Zhao-fa, et al. Modeling and residual life estimation of step stress accelerated degradation test[J]. Journal of Mechanical Engineering, 2014, 50(16): 33-40.
20	Lim H, Yum B J. Optimal design of accelerated degradation tests based on wiener process model[J]. Journal of Applied Statistics, 2011, 38(2): 309-325.
21	李洪洲, 杨兆军, 许彬彬, 等. 数控机床可靠性评估试验周期设计[J]. 吉林大学学报: 工学版, 2016, 46(5): 1520-1527.
	Li Hong-zhou, Yang Zhao-jun, Xu Bin-bin, et al. Design of testing period for reliability assessment of NC machine tools[J]. Journal of Jilin University(Engineering and Technology Edition), 2016, 46(5): 1520-1527.
22	Ng H K T, Balakrishnan N, Chan P S. Optimal sample size allocation for tests with multiple levels of stress with extreme value regression[J]. Naval Research Logistics, 2007, 54(3): 237-249.
23	Meeker W Q, Luis A E. Statistical Methods for Reliability Data[M]. New York: John Wiley &Sons, 1998.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

[1]	杨海吉,何佳龙,李国发,王立鼎,王思远. 改进失效模式和影响分析方法在加工中心主轴系统风险分析中的应用[J]. 吉林大学学报(工学版), 2022, 52(2): 345-352.
[2]	董伟智,张爽,朱福. 基于可拓层次分析法的沥青混合料路用性能评价[J]. 吉林大学学报(工学版), 2021, 51(6): 2137-2143.
[3]	王芳荣, 郭柏苍, 金立生, 高琳琳, 岳欣羽. 次任务驾驶安全评价指标筛选及其权值计算[J]. 吉林大学学报(工学版), 2017, 47(6): 1710-1715.
[4]	王智远, 李国栋, 王勇华. 基于AHP-TOPSIS的桥梁设计方案优选决策模型[J]. 吉林大学学报(工学版), 2017, 47(2): 478-482.
[5]	李显生, 李明明, 任有, 严佳晖, 陈小夏. 城市不同道路线形下的驾驶人注视特性[J]. 吉林大学学报(工学版), 2016, 46(5): 1447-1452.
[6]	赵丁选, 王倩, 张祝新. 基于层次分析法的可拓学理论对舰载直升机可靠性的评估[J]. 吉林大学学报(工学版), 2016, 46(5): 1528-1531.
[7]	李欢利, 郭立红, 王心醉, 李小明, 董月芳, 方艳超. 基于加权Gabor滤波器的虹膜识别[J]. 吉林大学学报(工学版), 2014, 44(01): 196-202.
[8]	闫清东, 刘树成, 魏巍, 杨汇斌. 基于改进雷达图法的变矩器匹配评价[J]. 吉林大学学报(工学版), 2013, 43(06): 1510-1516.
[9]	郝庆波, 杨兆军, 陈传海, 陈菲, 李国发. 基于区间层次分析法的数控机床可靠性预计[J]. , 2012, 42(04): 845-850.
[10]	申桂香, 邵娜, 张英芝, 何宇, 王晓峰. 基于可拓理论的数控机床顾客满意度评价[J]. 吉林大学学报(工学版), 2011, 41(增刊1): 164-167.
[11]	陈勇¹,陈潇凯¹,林逸^1,2. 改进雷达图评价方法在汽车综合性能评价中的应用[J]. 吉林大学学报(工学版), 2011, 41(6): 1522-1526.
[12]	韩豹,吴文福,权龙哲. 水平圆盘式苗间锄草装置的多目标优化设计及仿真[J]. 吉林大学学报(工学版), 2011, 41(03): 692-696.
[13]	申桂香,邵娜,张英芝,何宇,郑锐,陈炳锟. 基于可拓学理论的数控机床可靠性评价[J]. 吉林大学学报(工学版), 2011, 41(01): 106-0109.
[14]	王祥锋,韩万金. 跨音压气机转子多目标气动优化设计[J]. 吉林大学学报(工学版), 2010, 40(01): 299-0304.
[15]	张水潮,任刚,王炜. 面向交通规划的城市道路交通拥堵度分析模型[J]. 吉林大学学报(工学版), 2009, 39(增刊2): 111-0115.

基于Gamma过程的加速退化试验多目标优化设计

Multi⁃objective optimization design of accelerated degradation test based on Gamma process

RICH HTML

PDF (PC)

摘要/Abstract

引用本文

使用本文

图/表 4

参考文献 23

相关文章 15

Metrics

本文评价

推荐阅读 0

方案	n₁	n₂	n₃	S₁	S₂	S₃	R₁	R₂
1	14	3	13	90	200	91	0.2296	0.7704
2	14	4	12	90	200	92	0.2787	0.7213
3	13	4	13	92	200	94	0.2789	0.7211
4	13	5	12	92	200	94	0.3212	0.6788
5	7	6	17	50	200	105	0.3752	0.6248
6	7	6	17	50	200	106	0.3758	0.6242
7	7	6	17	50	200	107	0.3763	0.6237
8	6	7	17	50	200	105	0.4057	0.5943
9	6	7	17	50	200	107	0.4065	0.5935
10	7	7	16	50	200	105	0.4078	0.5922
11	7	7	16	50	200	107	0.4086	0.5914
12	7	8	15	50	200	106	0.4372	0.5628
13	7	8	15	50	200	107	0.4375	0.5625
14	8	8	14	50	200	108	0.4400	0.5600
15	8	9	13	50	200	109	0.4664	0.5336
16	9	9	12	50	200	110	0.4689	0.5311
17	9	9	12	50	200	113	0.4700	0.5300
18	9	10	11	50	200	110	0.4924	0.5076
19	8	11	11	50	200	112	0.5119	0.4881
20	9	11	10	50	200	108	0.5135	0.4865
21	9	11	10	50	200	111	0.5140	0.4860
22	9	12	9	50	200	111	0.5335	0.4665
23	9	12	9	50	200	114	0.5340	0.4660
24	9	13	8	50	200	112	0.5515	0.4485
25	10	13	7	50	200	110	0.5537	0.4463
26	10	13	7	50	200	118	0.5548	0.4452
27	10	14	6	50	200	114	0.5705	0.4295
28	10	15	5	50	200	113	0.5856	0.4144
29	10	15	5	50	200	114	0.5857	0.4143
30	11	15	4	50	200	119	0.5884	0.4116

方案	n₁	n₂	n₃	S₁	S₂	S₃	μ₁	μ₂
1	14	3	13	90	200	91	0.364 170	0.205 823
2	14	4	12	90	200	92	0.228 190	0.128 972
3	13	4	13	92	200	94	0.227 640	0.128 659
4	13	5	12	92	200	94	0.110 500	0.062 500
5	7	6	17	50	200	105	0.039 000	0.022 100
6	7	6	17	50	200	106	0.040 709	0.023 010
7	7	6	17	50	200	107	0.042 094	0.023 790
8	6	7	17	50	200	105	0.123 511	0.069 810
9	6	7	17	50	200	107	0.125 727	0.071 060
10	7	7	16	50	200	105	0.129 327	0.073 090