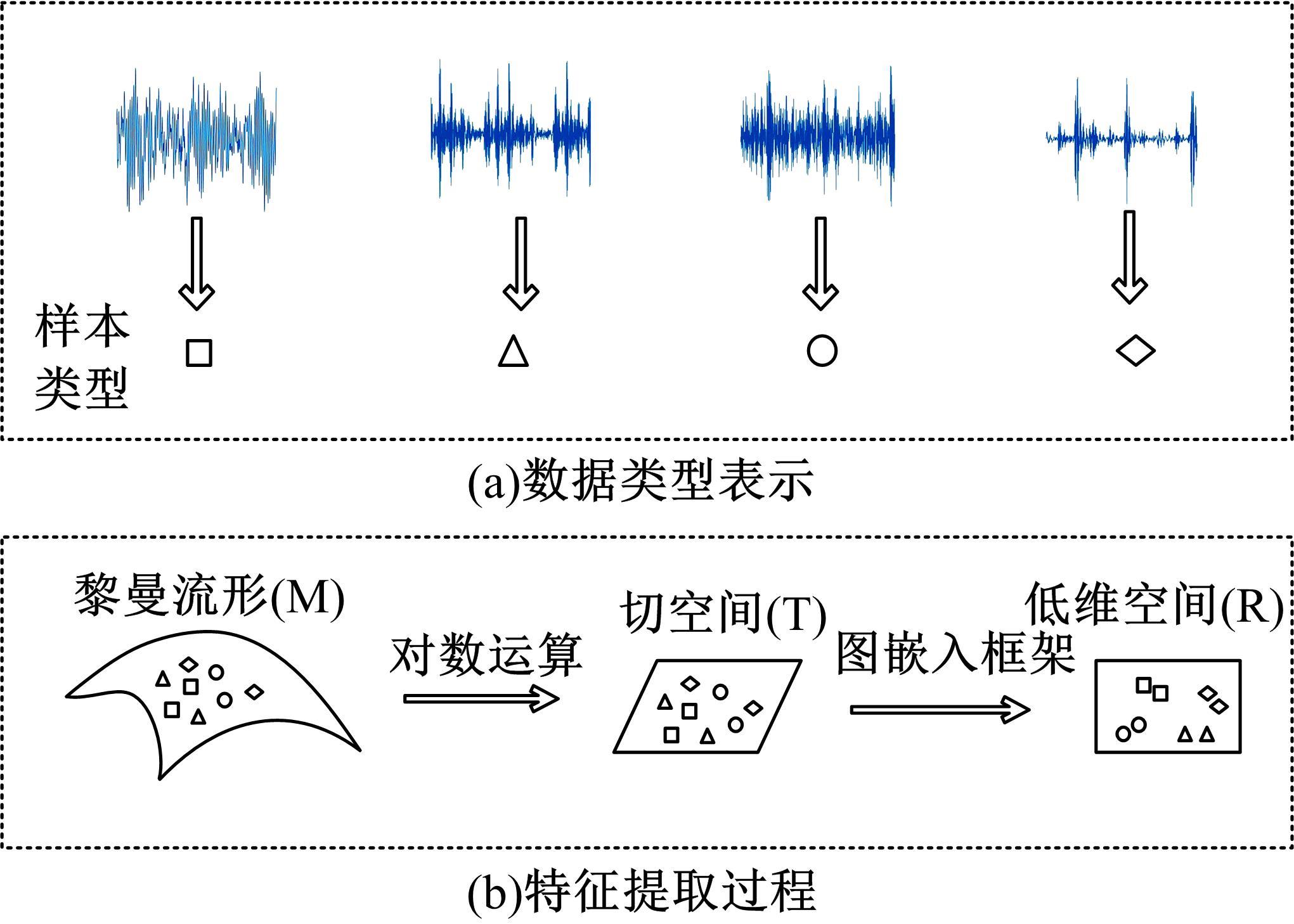
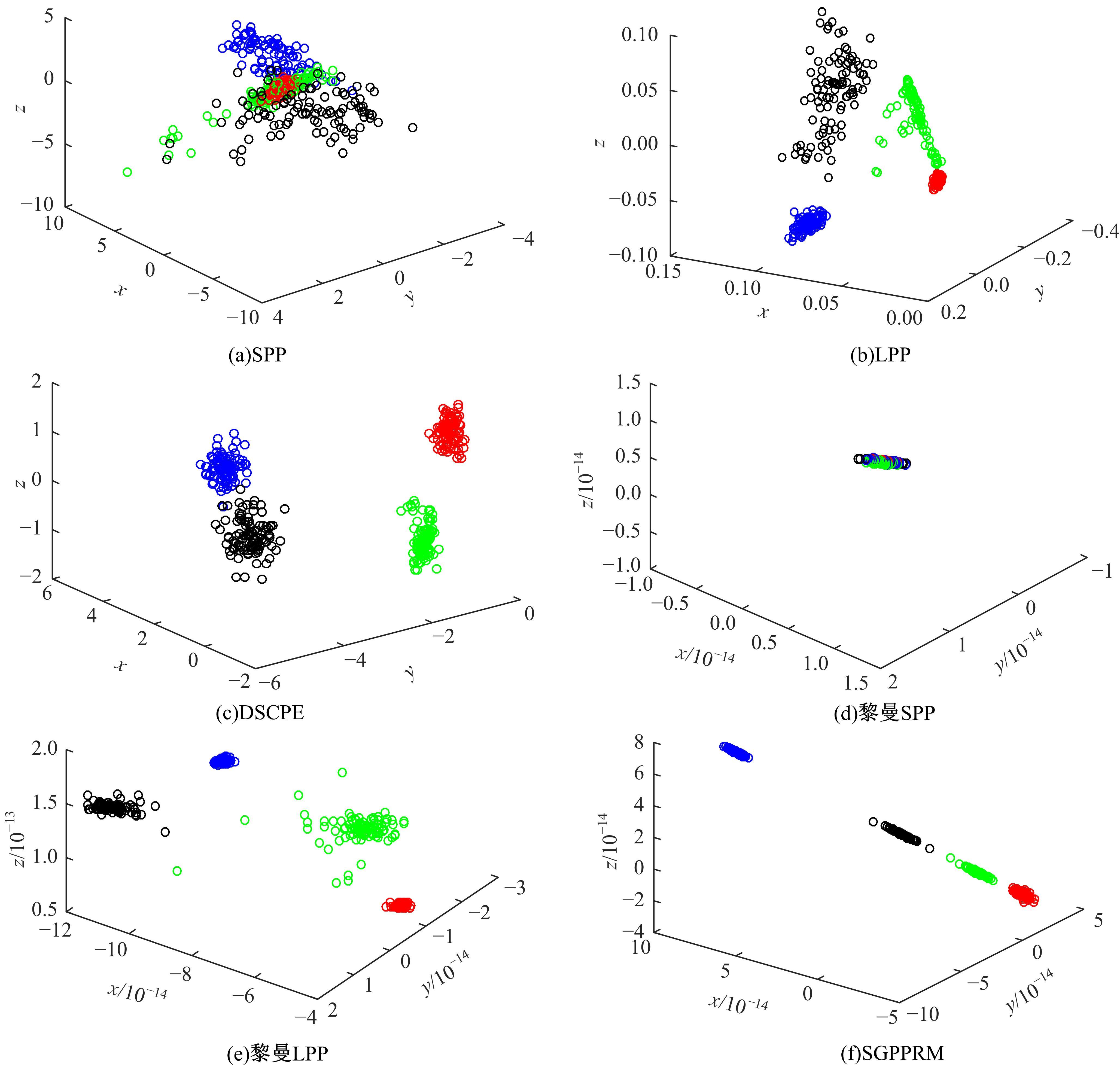
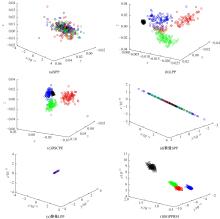
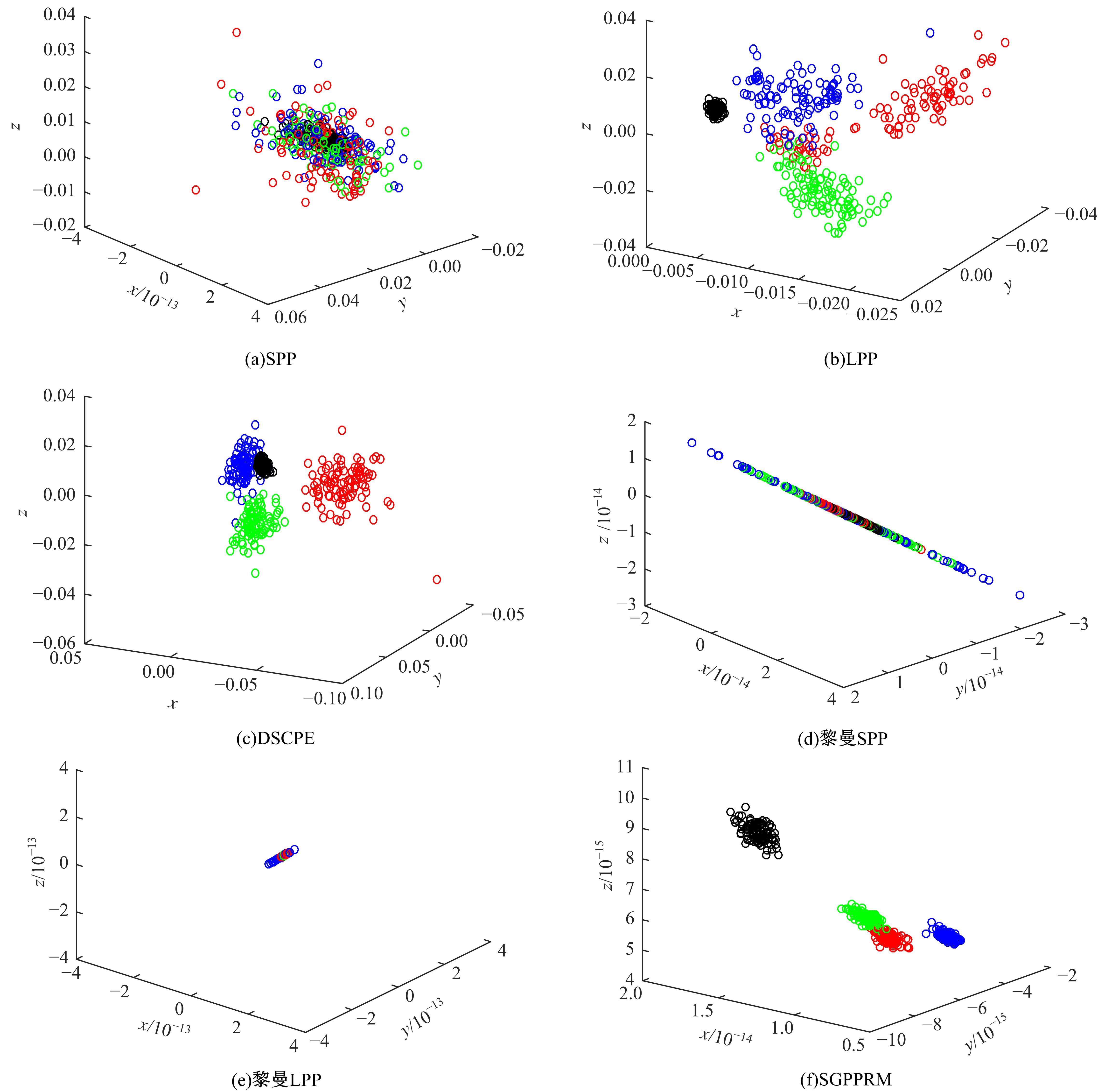
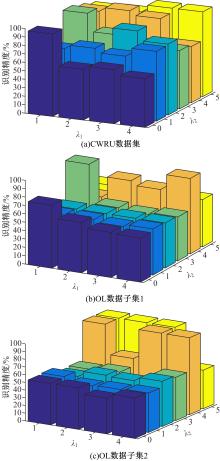
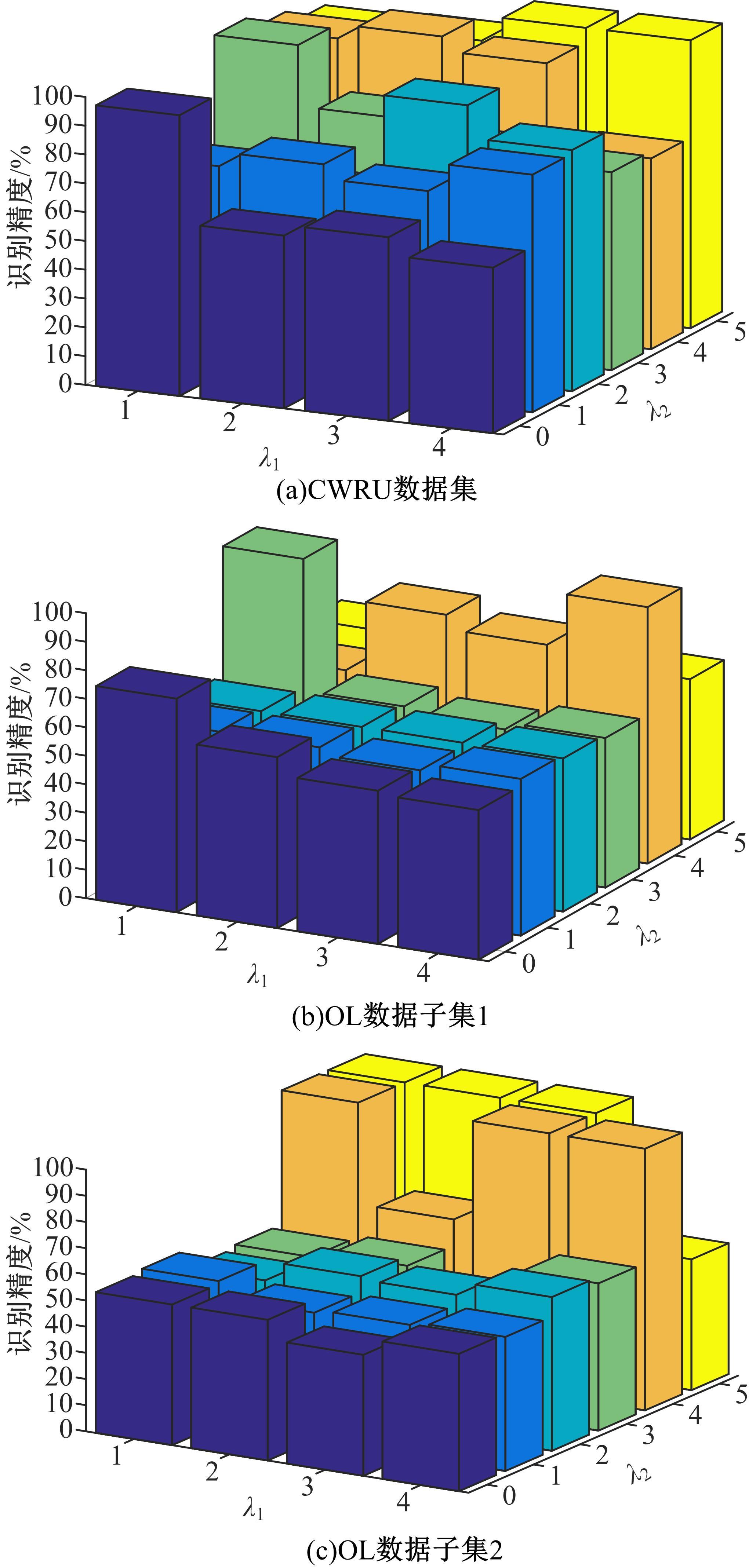
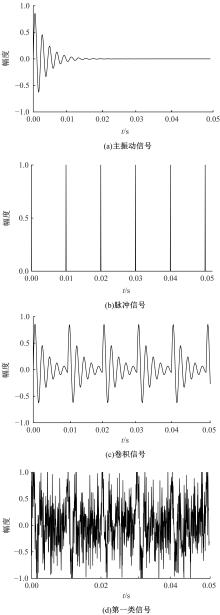
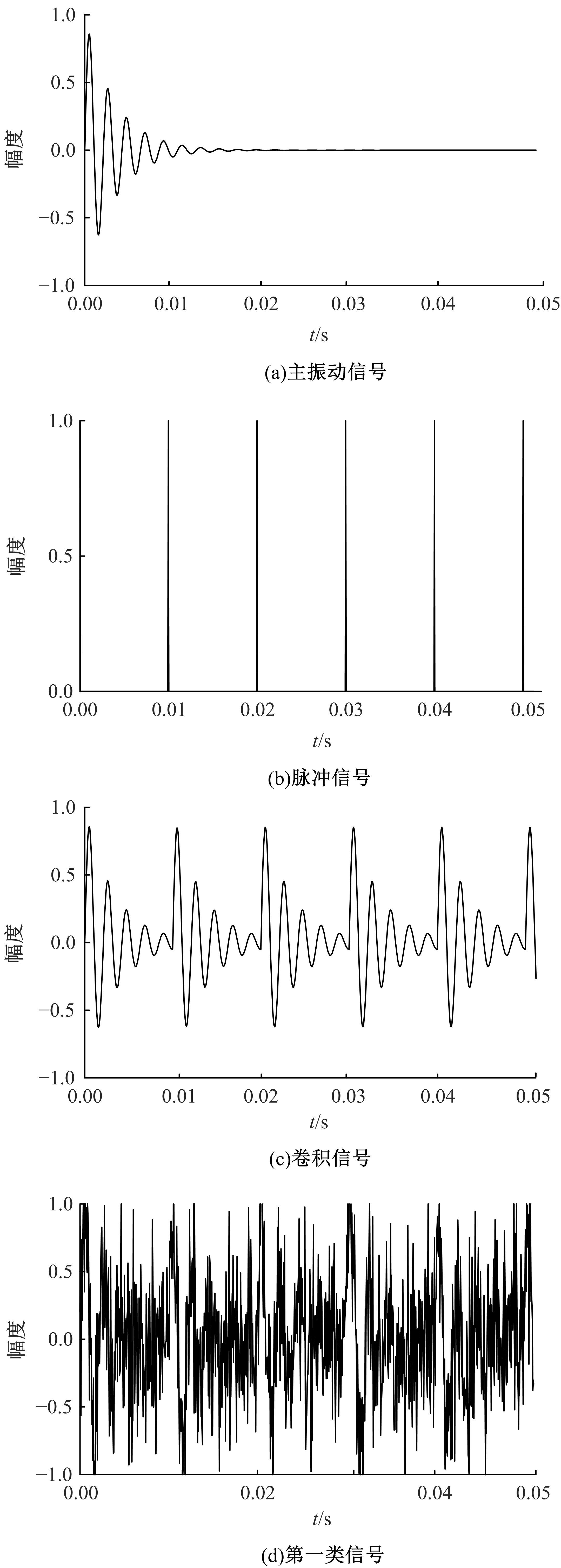
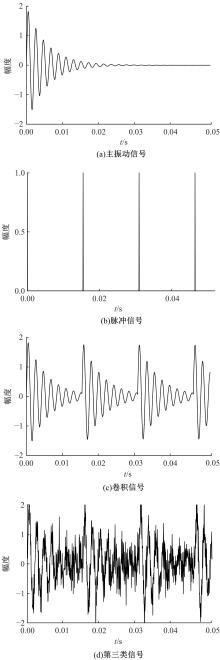
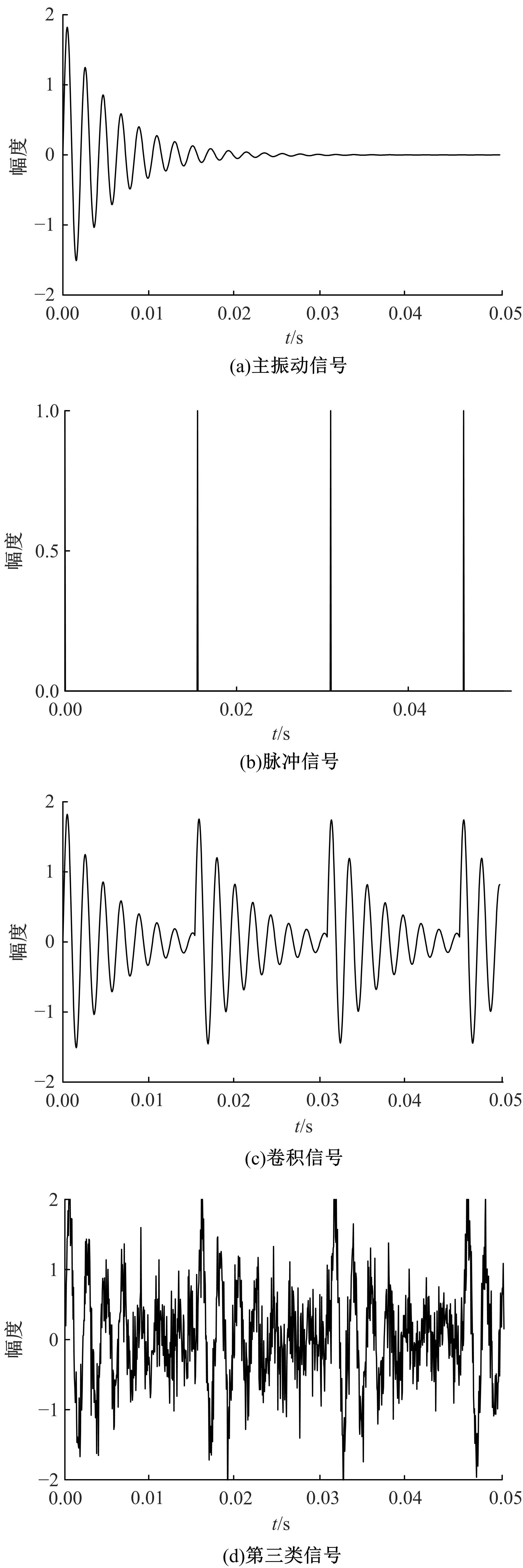
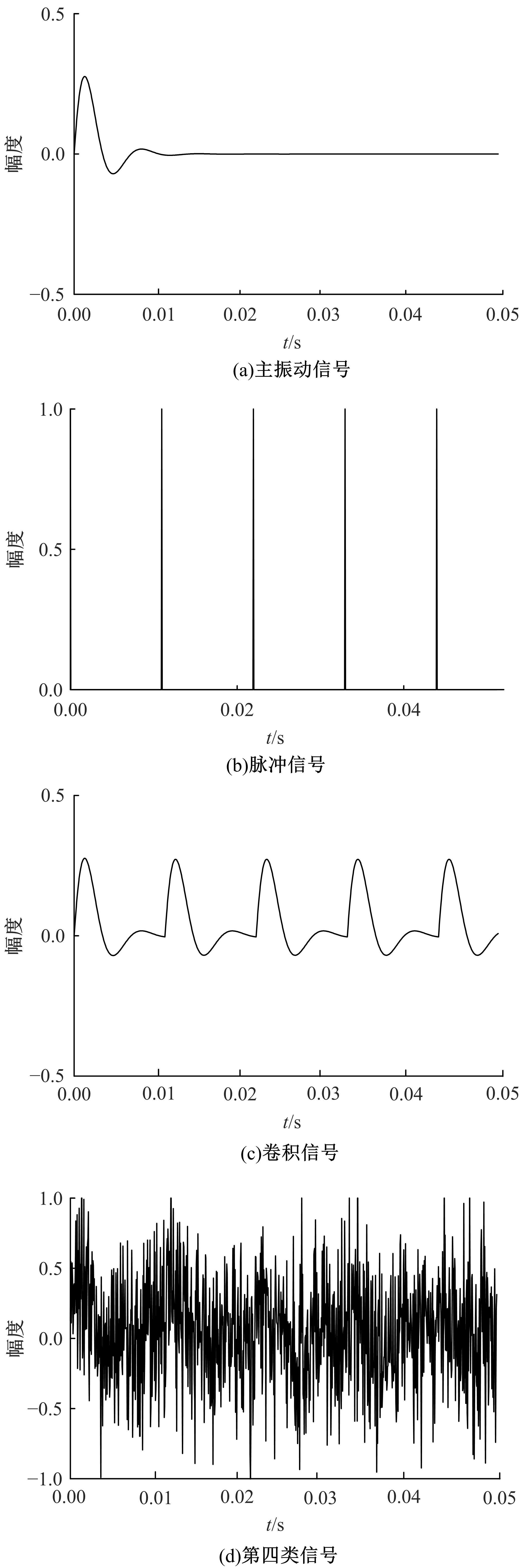
Journal of Jilin University(Engineering and Technology Edition) ›› 2021, Vol. 51 ›› Issue (6): 2268-2279.doi: 10.13229/j.cnki.jdxbgxb20200589
Feature extraction of sparse graph preserving projection based on Riemannian manifold
Yuan-hong LIU1( ),Pan-pan GUO1,Yan-sheng ZHANG1(
),Pan-pan GUO1,Yan-sheng ZHANG1( ),Xin LI2
),Xin LI2
- 1.Northeast Petroleum University,Institute of Electrical Information Engineering,Daqing 163318,China
2.CNPC Daqing Drilling & Exploration Engineering Company,Daqing 163458,China
CLC Number:
- TP273
| 1 | Dong S J, Sun D H, Tang B P, et al. A fault diagnosis method for rotating machinery based on PCA and morlet kernel SVM[J]. Mathematical Problems in Engineering, 2014, 2014(10): No. 293878. |
| 2 | Zhao X L,Ming P J. Fault diagnosis of rolling bearing based on feature reduction with global-local margin fisher analysis[J]. Neurocomputing, 2018, 315: 447-464. |
| 3 | Gao Z W, Cecati C, Ding S X. A survey of fault diagnosis and fault-tolerant techniques—part I: fault diagnosis with model-based and signal-based approaches[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3757-3767. |
| 4 | Belkin M, Niyogi P. Laplacian eigenmaps for dimensionality reduction and data representation[J]. Neural Computation, 2003, 15(6):1373-1396. |
| 5 | 李勇, 陈贺新, 赵刚, 等. 基于可变k近邻LLE数据降维的图像检索方法[J]. 吉林大学学报:工学版, 2008, 38(4): 946-949. |
| Li Yong, Chen He-xin, Zhao Gang, et al. Image retrieval method based on variable k nearest neighbor [J]. Journal of Jilin University (Engineering and Technology Edition), 2008, 38(4): 946-949. | |
| 6 | 孟广伟, 冯昕宇, 周立明,等. 基于降维算法的结构可靠性分析[J]. 吉林大学报:工学版, 2017, 47(1): 174-179. |
| Meng Guang-wei, Feng Xin-yu, Zhou Li-ming, et al. Structural reliability analysis based on dimension reduction algorithm[J]. Journal of Jilin University (Engineering and Technology Edition),2017,47(1):174-179. | |
| 7 | Qiao L S, Chen S C, Tan X Y. Sparsity preserving projections with applications to face recognition[J]. Pattern Recognition, 2010, 43(1):331-341. |
| 8 | 殷俊, 杨万扣. 核稀疏保持投影及生物特征识别应用[J]. 电子学报, 2013, 41(4): 639-645. |
| Yin Jun, Yang Wan-kou. Nuclear sparse preserving projection and application of biometric recognition[J]. Chinese Journal of Electronics, 2013, 41(4): 639-645. | |
| 9 | Yan S C, Dong X, Zhang B Y, et al. Graph embedding and extensions: a general framework for dimensionality reduction[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2007, 29(1): 40-51. |
| 10 | Lou S J, Zhao X M, Chuang Y L, et al. Graph regularized sparsity discriminant analysis for face recognition[J]. Sensors and Actuators, 2016, 173: 290-297. |
| 11 | Zhang L M, Chen S C, Qiao L S. Graph optimization for dimensionality reduction with sparsity constraints[J]. Pattern Recognition, 2012, 45(3):1205-1210. |
| 12 | Yang W K, Wang Z Y, Sun C Y. A collaborative representation based projections method for feature extraction[J]. Pattern Recognition, 2015, 48(1): 20-27. |
| 13 | Ma Y, Wu X H. Discriminant sparse and collaborative preserving embedding for bearing fault diagnosis[J]. Neurocomputing, 2018, 313: 259-270. |
| 14 | 蔡金金, 刘博, 马跃进, 等. 多黎曼流形的判别分析与融合[J]. 河北农业大学学报, 2019, 42(1): 114-121. |
| Cai Jin-jin, Liu Bo, Ma Yue-jin, et al. Discriminant analysis and fusion of multi Riemannian manifolds [J]. | |
| Journal of Agricultural University of Hebei, 2019, 42(1): 114-121. | |
| 15 | Harandi M, Salzmann M, Hartley R. Dimensionality reduction on spd manifolds: the emergence of geometry-aware methods[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2017, 40(1):48-62. |
| 16 | Xie X F, Zhu L Y, Gu Z H, et al. Classification of symmetric positive definite matrices based on bilinear isometric Riemannian embedding[J]. Pattern Recognition, 2019, 87: 94-105. |
| 17 | Cheng J, Ghosh A, Jiang T Z, et al. A Riemannian framework for orientation distribution function computing[J/OL]. [2020-06-03]. |
| 18 | Arsigny V, Fillard P, Pennec X, et al. Log-Euclidean metrics for fast and simple calculus on diffusion tensors[J]. Magnetic Resonance in Medicine, 2010, 56(2): 411-421. |
| 19 | Cherian A, Sra S, Banerjee A, et al. Jensen-bregman logdet divergence with application to efficient similarity search for covariance matrices[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2013, 35(9): 2161-2174. |
| 20 | Arsigny V, Fillard P, Pennec X, et al. Geometric means in a novel vector space structure on symmetric positive-definite matrices[J]. Siam Journal on Matrix Analysis & Applications, 2011, 29(1): 328-347. |
| 21 | Lovri´c M, Min-Oo M, Ruh E A. Multivariate normal distributions parametrized as a Riemannian symmetric space[J]. Journal of Multivariate Analysis, 2000, 74(1): 36-48. |
| 22 | He X F, Yan S C, Hu Y X, et al. Face recognition using laplacianfaces[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2005, 27(3): 328-340. |
| [1] | Hui ZHONG,Heng KANG,Ying-da LYU,Zhen-jian LI,Hong LI,Ruo-chuan OUYANG. Image manipulation localization algorithm based on channel attention convolutional neural networks [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(5): 1838-1844. |
| [2] | Xiao-long ZHU,Zhong XIE. Automatic construction of knowledge graph based on massive text data [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(4): 1358-1363. |
| [3] | Guang-qiu CHEN,Yu-cun CHEN,Jia-yue LI,Guang-wen LIU. Infrared and visible image fusion based on discrete nonseparable shearlet transform and convolutional sparse representation [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(3): 996-1010. |
| [4] | Tao XU,Ke MA,Cai-hua LIU. Multi object pedestrian tracking based on deep learning [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(1): 27-38. |
| [5] | De-feng HE,Jie LUO,Xiao-xiang SHU. Delay-feedback predictive cruise control of autonomous and connected vehicles [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(1): 349-357. |
| [6] | Dan-tong OUYANG,Cong MA,Jing-pei LEI,Sha-sha FENG. Knowledge graph embedding with adaptive sampling [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(2): 685-691. |
| [7] | Yi-bin LI,Jia-min GUO,Qin ZHANG. Methods and technologies of human gait recognition [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(1): 1-18. |
| [8] | Hong-yan WANG,He-lei QIU,Jia ZHENG,Bing-nan PEI. Visual tracking method based on low⁃rank sparse representation under illumination change [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(1): 268-277. |
| [9] | GENG Qing-tian, YU Fan-hua, WANG Yu-ting, GAO Qi-kun. New algorithm for vehicle type detection based on feature fusion [J]. 吉林大学学报(工学版), 2018, 48(3): 929-935. |
| [10] | DONG Qiang, LIU Jing-hong, ZHOU Qian-fei. Improved SURF algorithm used in image mosaic [J]. 吉林大学学报(工学版), 2017, 47(5): 1644-1652. |
| [11] | YIN Ming, ZHAN Yin-wei, PEI Hai-long. Co-sparse analysis operator learning for image fusion [J]. 吉林大学学报(工学版), 2016, 46(6): 2052-2058. |
| [12] | XIAO Zhong-jie. Recognition of digital image based on wavelet space feature spectrum entropy [J]. 吉林大学学报(工学版), 2015, 45(6): 1994-1998. |
| [13] | LIU Hong,SUN Shuang-zi,WANG Qing-yuan,LI Yan-zhong. PSO based feature extraction method for analog circuit fault information [J]. 吉林大学学报(工学版), 2015, 45(2): 675-680. |
| [14] | PAN Hai-yang, LIU Shun-an, YAO Yong-ming. Depth information-basd autonomous aerial refueling [J]. 吉林大学学报(工学版), 2014, 44(6): 1750-1756. |
| [15] | ZHA Chang-jun,WEI Sui,YANG Hai-rong,DING Da-wei. Special object recognition based on sparse representation in multiclass fusion sample [J]. 吉林大学学报(工学版), 2014, 44(3): 822-827. |
|
||