Journal of Jilin University(Engineering and Technology Edition) ›› 2019, Vol. 49 ›› Issue (4): 1144-1152.doi: 10.13229/j.cnki.jdxbgxb20180020

Previous Articles    

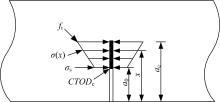
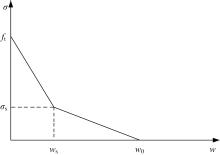
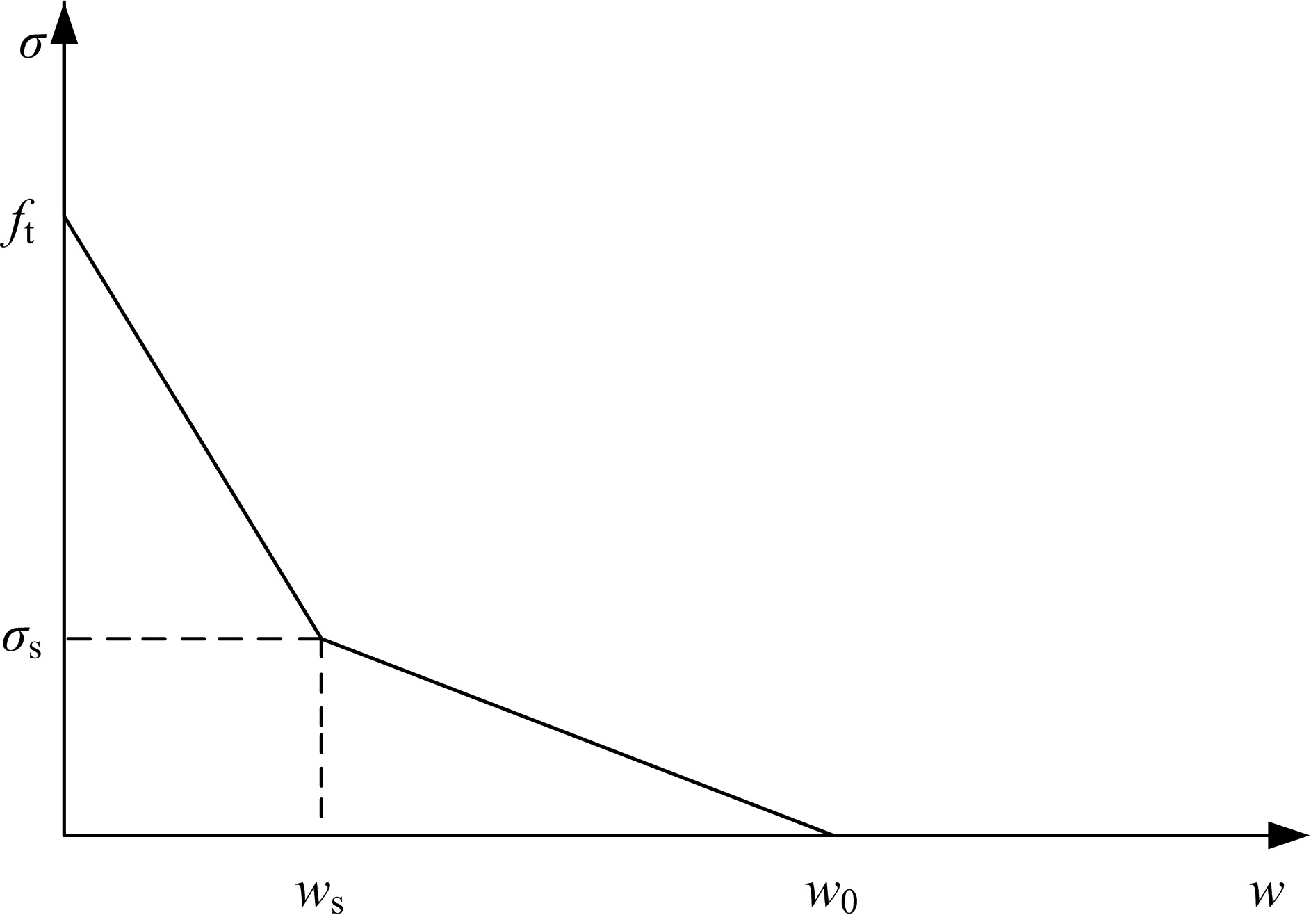
Determination of fracture toughness and softening traction⁃separation law of polypropylene fiber reinforced concrete

Ning⁃hui LIANG1,2(),Qing⁃xu MIAO1,2,Xin⁃rong LIU1,2,Ji⁃fei DAI3,Zu⁃liang ZHONG1,2   

  1. 1. School of Civil Engineering, Chongqing University, Chongqing 400045, China
    2. National Joint Engineering Research Center of Geohazards Prevention in the Reservoir Areas, Chongqing 400045, China
    3. China Construction Infrastructure Co, Ltd, Beijing 100044, China
  • Received:2018-01-08 Online:2019-07-01 Published:2019-07-16

RICH HTML

 2   

PDF (PC)

156

Abstract:

The three?point bending test was carried out on concrete notched beams with different amount of coarse and fine polypropylene(PP) fibers. Based on the double?K fracture theory, the influence of mixing method of PP fibers with different sizes on the fracture toughness and failure mechanism were discussed.The real cohesive toughness, the increment of initiation toughness and the bridge connection toughness were gained by the quantitative relationship between the initiation toughness, the unstable toughness and the cohesive toughness. In addition, The theoretical cohesive toughness was calculated from three kinds of ordinary concrete bilinear softening constitutive curves, which was compared with the real cohesive toughness to determine the bilinear softening traction?separation law of PFRC, which was suitable for different PP fiber incorporation conditions. The results show that PFRC has higher initiation toughness, unstable toughness and fracture energy compared with plain concrete. The enhancement effect of bridge connection toughness from bridging stress is very significant when 2 or 3 sizes of PP fibers are mixed. The 3 sizes of PP fibers play the role of bridging at different stages of crack propagation, and it serves a well function of toughening and strengthening. The bilinear softening traction?separation law proposed by Xu and Reinhardt is well applicable for PFRC when the correction coefficient is 6.

Key words: civil engineering, polypropylene fiber reinforced concrete, double?K fracture model, bilinear softening traction?separation law

CLC Number: 

  • TU528

Fig.1

Distribution of critical cohesive stress on fictitious crack zone"

Fig.2

Bilinear softening traction?separation law"

Table 1

Physical and mechanical properties of"

参 数 FF1 FF2 CF1
直径/mm 0.026 0.100 0.800
长度/mm 19 19 50
抗拉强度/MPa 641 322 706
弹性模量/GPa 4.5 4.9 7.4
断裂伸长率/% 40 15 10
密度/(g·cm-3) 0.91 0.91 0.95
推荐掺量/(kg·m-3) 0.9 0.9 6.0

Table 2

Amount of polypropylene fiber for different specimens"

试件编号 纤维种类 纤维掺量/(kg·m-3)
A0 无 0
A1 FF1 0.9
A2 FF2 0.9
A3 CF1 6.0
A4 FF1+CF1 0.6+5.4
A5 FF1+CF1 0.9+5.1
A6 FF1+CF1 1.2+4.8
A7 FF2+CF1 0.6+5.4
A8 FF2+CF1 0.9+5.1
A9 FF2+CF1 1.2+4.8
A10 FF1+FF2+CF1 0.45+0.45+5.1
A11 FF1+FF2+CF1 0.6+0.6+4.8

Fig.3

"

Table 3

Calculated results of double?K fracture parameters and fracture energy"

试件

编号

 CMOD c/μm C T O D c /μm P inl/N

K I c i n i

/(MPa·m1/2)

 P m a x /N a c/mm

K I c u n

/(MPa·m1/2)

G f

/(N·m-1)
A0 39.9 10 1665 0.561 2017 57 0.869 104.7
A1 48.1 13 1943 0.654 2441 59 1.133 147.6
A2 42.5 12 1503 0.506 1929 61 0.960 113.3
A3 51.1 15 1807 0.608 2265 61 1.132 403.1
A4 51.2 16 1727 0.582 2243 62 1.120 537.9
A5 58.8 21 1850 0.623 2457 63 1.336 562.0
A6 54.7 18 1752 0.590 2276 64 1.285 535.0
A7 54.8 18 1797 0.605 2351 63 1.287 480.7
A8 56.5 19 1755 0.591 2284 64 1.282 544.2
A9 47.2 16 1627 0.548 2177 64 1.272 433.6
A10 44.9 18 1983 0.670 2552 63 1.356 537.7
A11 57.3 20 1930 0.650 2580 64 1.454 608.8

Table 4

Increment of initiation toughness and bridge connection toughness of polypropylene fiber"

试件编号 K I c c s Δ K I c i n i s
A0 0 0
A1 0.171 0.093
A2 0.146 -0.055
A3 0.216 0.047
A4 0.230 0.021
A5 0.405 0.062
A6 0.387 0.029
A7 0.374 0.044
A8 0.383 0.030
A9 0.416 -0.013
A10 0.378 0.109
A11 0.496 0.089

Table 5

Comparison between K I c , T c and K I c , E c "

试件编号 K I c , T c K I c , E c （Petersson) K I c , E c （CEB?FIP Model Code 1990) K I c , E c （徐世烺和Reinhardt)
λ=5 λ=6 λ=7 λ=8 λ=9 λ=10
∑ i = 1 11 η i 0.601 0.594 0.274 0.149 0.161 0.220 0.279 0.305
A0?1 0.287 0.479 0.344 0.328 0.299 0.283 0.272 0.265 0.260
A0?2 0.335 0.510 0.366 0.348 0.317 0.299 0.288 0.280 0.274
A0?3 0.304 0.415 0.298 0.283 0.259 0.245 0.236 0.230 0.225
η 0 0.08 0.004 0.002 0.0025 0.005 0.007 0.009 0.010
A1?1 0.489 0.525 0.523 0.494 0.445 0.442 0.431 0.419 0.411
A1?2 0.523 0.622 0.620 0.587 0.532 0.529 0.508 0.493 0.483
A1?3 0.424 0.538 0.536 0.506 0.460 0.458 0.441 0.429 0.420
η 1 0.024 0.023 0.011 0.003 0.003 0.0038 0.006 0.008
A2?1 0.588 0.730 0.725 0.692 0.624 0.619 0.594 0.577 0.564
A2?2 0.419 0.630 0.627 0.596 0.540 0.536 0.515 0.501 0.490
A2?3 0.355 0.555 0.552 0.524 0.475 0.474 0.456 0.443 0.434
η 2 0.105 0.101 0.07 0.031 0.029 0.02 0.015 0.012
A3?1 0.493 0.547 0.546 0.509 0.461 0.458 0.441 0.428 0.419
A3?2 0.549 0.837 0.836 0.773 0.692 0.689 0.653 0.631 0.616
A3?3 0.526 0.678 0.677 0.630 0.568 0.563 0.539 0.523 0.512
η 3 0.109 0.108 0.06 0.023 0.02 0.013 0.011 0.01
A4?1 0.517 0.617 0.616 0.571 0.516 0.512 0.491 0.476 0.466
A4?2 0.931 1.06 1.05 0.972 0.863 0.848 0.807 0.779 0.759
A4?3 0.405 0.632 0.632 0.585 0.527 0.523 0.501 0.486 0.475
η 4 0.077 0.051 0.037 0.019 0.021 0.025 0.031 0.037
A5?1 0.791 0.803 0.802 0.743 0.667 0.658 0.630 0.610 0.595
A5?2 0.628 0.771 0.770 0.712 0.639 0.632 0.604 0.586 0.571
A5?3 - - - - - - - - -
η 5 0.020 0.020 0.009 0.015 0.017 0.026 0.031 0.041
A6?1 0.649 0.759 0.757 0.701 0.630 0.623 0.596 0.578 0.564
A6?2 0.740 0.893 0.892 0.823 0.735 0.724 0.691 0.668 0.651
A6?3 0.695 0.845 0.843 0.781 0.699 0.689 0.659 0.638 0.622
η 6 0.058 0.057 0.017 0.0004 0.0001 0.006 0.013 0.02
A7?1 0.713 0.828 0.828 0.763 0.683 0.673 0.644 0.623 0.607
A7?2 0.836 0.960 0.958 0.885 0.788 0.776 0.740 0.715 0.697
A7?3 0.681 0.783 0.781 0.726 0.652 0.644 0.616 0.598 0.583
η 7 0.040 0.038 0.007 0.004 0.007 0.018 0.03 0.04
A8?1 0.805 1.038 1.037 0.952 0.846 0.831 0.791 0.764 0.744
A8?2 0.628 0.741 0.739 0.687 0.617 0.611 0.585 0.567 0.553
A8?3 0.691 0.833 0.832 0.768 0.687 0.678 0.648 0.627 0.612
η 8 0.087 0.086 0.031 0.002 0.001 0.004 0.009 0.016
A9?1 0.541 0.677 0.676 0.630 0.568 0.563 0.540 0.523 0.512
A9?2 0.794 0.943 0.942 0.868 0.773 0.761 0.726 0.701 0.683
A9?3 0.724 0.880 0.879 0.811 0.725 0.715 0.682 0.660 0.643
η 9 0.065 0.064 0.021 0.001 0.0016 0.006 0.013 0.019
A10?1 0.716 0.767 0.766 0.708 0.635 0.628 0.610 0.582 0.568
A10?2 0.783 0.864 0.863 0.797 0.713 0.703 0.671 0.650 0.633
A10?3 0.688 0.755 0.754 0.699 0.627 0.621 0.594 0.576 0.562
η 10 0.014 0.013 0.0004 0.015 0.019 0.034 0.048 0.06
A11?1 0.789 0.774 0.773 0.716 0.643 0.635 0.608 0.589 0.575
A11?2 0.806 0.848 0.847 0.781 0.699 0.689 0.659 0.637 0.621
A11?3 - - - - - - - - -
η 11 0.002 0.002 0.006 0.032 0.037 0.054 0.068 0.080
1 Xu T , Stewart R , Fan J , et al . Bridging crack propagation at the atomistic and mesoscopic scale for BCC⁃Fe with hybrid multiscale methods[J]. Engineering Fracture Mechanics, 2016, 155: 166⁃182.
2 Liang N , Dai J , Liu X . Study on tensile damage constitutive model for multiscale polypropylene fiber concrete[J]. Advances in Materials Science and Engineering, 2016, 9168984.
3 邓宗才 . 混杂纤维增强超高性能混凝土弯曲韧性与评价方法[J]. 复合材料学报, 2016, 33(6):1274⁃1280.
Deng Zong⁃cai . Flexural toughness and character⁃ization method of hybrid fibers reinforced ultra⁃high performance concrete[J]. Acta Materiae Compositae Sinica, 2016, 33(6): 1274⁃1280.
4 夏冬桃, 刘向坤, 夏广政, 等 . 混杂纤维增强高性能混凝土弯曲韧性研究[J]. 华中科技大学学报: 自然科学版, 2013, 41(6): 108⁃112.
Xia Dong⁃tao , Liu Xiang⁃kun , Xia Guang⁃zheng , et al . Flexural toughness of high⁃performance hybrid fiber reinforced concrete[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2013, 41(6): 108⁃112.
5 Caggiano A , Gambarelli S , Martinelli E , et al . Experimental characterization of the post⁃cracking response in hybrid steel/polypropylene fiber⁃ reinforced concrete[J]. Construction & Building Materials, 2016, 125:1035⁃1043.
6 陆洲导, 俞可权 . 高温后混凝土断裂韧度及软化本构曲线确定[J]. 同济大学学报:自然科学版, 2012, 40(9): 1306⁃1311.
Lu Zhou⁃dao , Yu Ke⁃quan . Determination of residual fracture toughness and softening traction⁃separation law of post⁃fire concrete[J]. Journal of Tongji University (Nature Science), 2012, 40(9): 1306⁃1311.
7 Xu S L . Determination of parameters in the bilinear, Reinhardt’s and exponentially nonlinear softening curves and their physical meaning[C]∥Werkstoffe und Werkstoffprüfung im Bauwesen, Hamburg,Libri BOD,1999: 410⁃424.
8 徐世烺, 熊松波, 李贺东, 等 . 混凝土断裂参数厚度尺寸效应的定量表征与机理分析[J]. 土木工程学报, 2017, 50(5): 57⁃71.
Xu Shi⁃lang , Xiong Song⁃bo , Li He⁃dong , et al . Quantitative characterization and mechanism analysis on thickness⁃dependent size effect of concrete fracture[J]. China Civil Engineering Journal, 2017, 50(5): 57⁃71.
9 Amin A , Foster S J , Muttoni A . Derivation of the σ‐w relationship for SFRC from prism bending tests[J]. Structural Concrete, 2015, 16(1): 93⁃105.
10 Li D S , Hai C , Ou J . Fracture behavior and damage evaluation of polyvinyl alcohol fiber concrete using acoustic emission technique[J]. Materials & Design, 2012, 40: 205⁃211.
11 Almusallam T , Ibrahim S M , Al⁃Salloum Y , et al . Analytical and experimental investigations on the fracture behavior of hybrid fiber reinforced concrete[J]. Cement & Concrete Composites, 2016, 74: 201⁃217.
12 Dong W , Wu Z , Zhou X , et al . A comparative study on two stress intensity factor⁃based criteria for prediction of mode⁃I crack propagation in concrete[J]. Engineering Fracture Mechanics, 2016, 158:39⁃58.
13 Kazemi M T , Golsorkhtabar H , Beygi M H A , et al . Fracture properties of steel fiber reinforced high strength concrete using work of fracture and size effect methods[J]. Construction & Building Materials, 2017, 142: 482⁃489.
14 Tada H , Paris P C , Irwin G R . The Stress Analysis of Cracks Handbook[M]. New York:Wiley,2000.
15 陈江义, 刘保元 . 纤维断裂损伤对复合材料板中导波频散特性的影响[J]. 吉林大学学报:工学版, 2017, 47(1): 180⁃184.
Chen Jiang⁃yi , Liu Bao⁃yuan . Influence of fiber fracture damage on dispersion characteristic of guided wave in composite plate[J]. Journal of Jilin University(Engineering and Technology Edition), 2017, 47(1): 180⁃184.
16 Peterson P E . Crack Growth and Development of Fracture Zone in Plane Concrete and Similar Materials[M]. Lund: Division of Building Materials, 1981.
17 CEB. CEB⁃FIP model code 1990, Bulletin D information, No,213/214[S].
18 Reinhardt H W , Xu S . Crack extension resistance based on the cohesive force in concrete[J]. Engin eering Fracture Mechanics, 1999, 64(5): 563⁃587.
19 Awinda K , Chen J , Barnett S J . Investigating geometrical size effect on the flexural strength of the ultra high performance fiber reinforced concrete using the cohesive crack model[J]. Construction & Building Materials, 2016, 105: 123⁃131.
20 赵艳华, 聂玉强, 徐世烺 . 混凝土断裂能的边界效应确定法[J]. 工程力学, 2007, 24(1): 56⁃61.
Zhao Yan⁃hua , Nie Yu⁃qiang , Xu Shi⁃lang . Deter⁃mination of boundary effect on fracture of concrete[J]. Engineering Mechanics, 2007, 24(1): 56⁃61.
[1] Lei ZHANG,Bao⁃guo LIU,Zhao⁃fei CHU. Model test of the influence on shield shaft owing to water loss settlement of deep sandstone aquifer layer [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(3): 788-797.
[2] ZHENG Yi-feng, ZHAO Qun, BAO Wei, LI Zhuang, YU Xiao-fei. Wind resistance performance of long-span continuous rigid-frame bridge in cantilever construction stage [J]. 吉林大学学报(工学版), 2018, 48(2): 466-472.
[3] NI Ying-sheng, SUN Qi-xin, MA Ye, XU Dong. Calculation of capacity reinforcement about composite box girder with corrugated steel webs based on tensile stress region theory [J]. 吉林大学学报(工学版), 2018, 48(1): 148-158.
[4] WANG Teng, ZHOU Ming-ru, MA Lian-sheng, QIAO Hong-xia. Fracture grouting crack growth of collapsible loess based on fracture theory [J]. 吉林大学学报(工学版), 2017, 47(5): 1472-1481.
[5] ZHENG Yi-feng, MAO Jian, LIANG Shi-zhong, ZHENG Chuan-feng. Negative skin friction of pile foundation considering soil consolidation in high fill site [J]. 吉林大学学报(工学版), 2017, 47(4): 1075-1081.
[6] LI Jing, WANG Zhe. Mechanical characteristics of concrete under true triaxial loading condition [J]. 吉林大学学报(工学版), 2017, 47(3): 771-777.
[7] GUO Nan, ZHANG Ping-yang, ZUO Yu, ZUO Hong-liang. Bending performance of glue-lumber beam reinforced by bamboo plyboard [J]. 吉林大学学报(工学版), 2017, 47(3): 778-788.
[8] ZHANG Jing, LIU Xiang-dong. Prediction of concrete strength based on least square support vector machine optimized by chaotic particle swarm optimization [J]. 吉林大学学报(工学版), 2016, 46(4): 1097-1102.
[9] GUO Xue-dong, MA Li-jun, ZHANG Yun-long. Analytical solution of the double joint layer composite beam with shear-slip under vertical concentrated load [J]. 吉林大学学报(工学版), 2016, 46(2): 432-438.
[10] HOU Zhong-ming, WANG Yuan-qing, XIA He, ZHANG Tian-shen. Simply-supported steel-concrete composite beams under moving load [J]. 吉林大学学报(工学版), 2015, 45(5): 1420-1427.
[11] ZHANG Yan-ling, SUN Tong, HOU Zhong-ming, LI Yun-sheng. Bending-torsion characteristics of steel-concrete curved composite beams stiffened with diaphragms [J]. 吉林大学学报(工学版), 2015, 45(4): 1107-1114.
[12] WANG Chun-gang, ZHANG Zhuang-nan, ZHAO Da-qian, CAO Yu-fei. Experimental investigation of Σ-section channel steel with complex edge stiffeners and web holes under axial compression [J]. 吉林大学学报(工学版), 2015, 45(3): 788-796.
[13] LI Hai-feng,GUO Xiao-nong,LUO Yong-feng,GAO Xuan-neng. Collapse resistance behavior of Ferris wheel with stay cables [J]. 吉林大学学报(工学版), 2015, 45(2): 406-413.
[14] GUO Jun-ping, DENG Zong-cai, LU Hai-bo, LIN Jin-song. Experiment on shear behavior of reinforced concrete beams strengthened with prestressed high strength steel wire mesh [J]. 吉林大学学报(工学版), 2014, 44(4): 968-977.
[15] WANG Jia-chun, YAN Pei-yu. Probabilistic analysis of rebar rust in concrete under marine environment [J]. 吉林大学学报(工学版), 2014, 44(2): 352-357.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
Copyright © Journal of Jilin University(Engineering and Technology Edition), All Rights Reserved.
Tel: +86-431-85095297　Fax: +86-431-85094074　E-mail: xbgxb@jlu.edu.cn
Powered by Beijing Magtech Co. Ltd