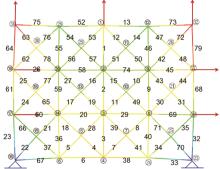
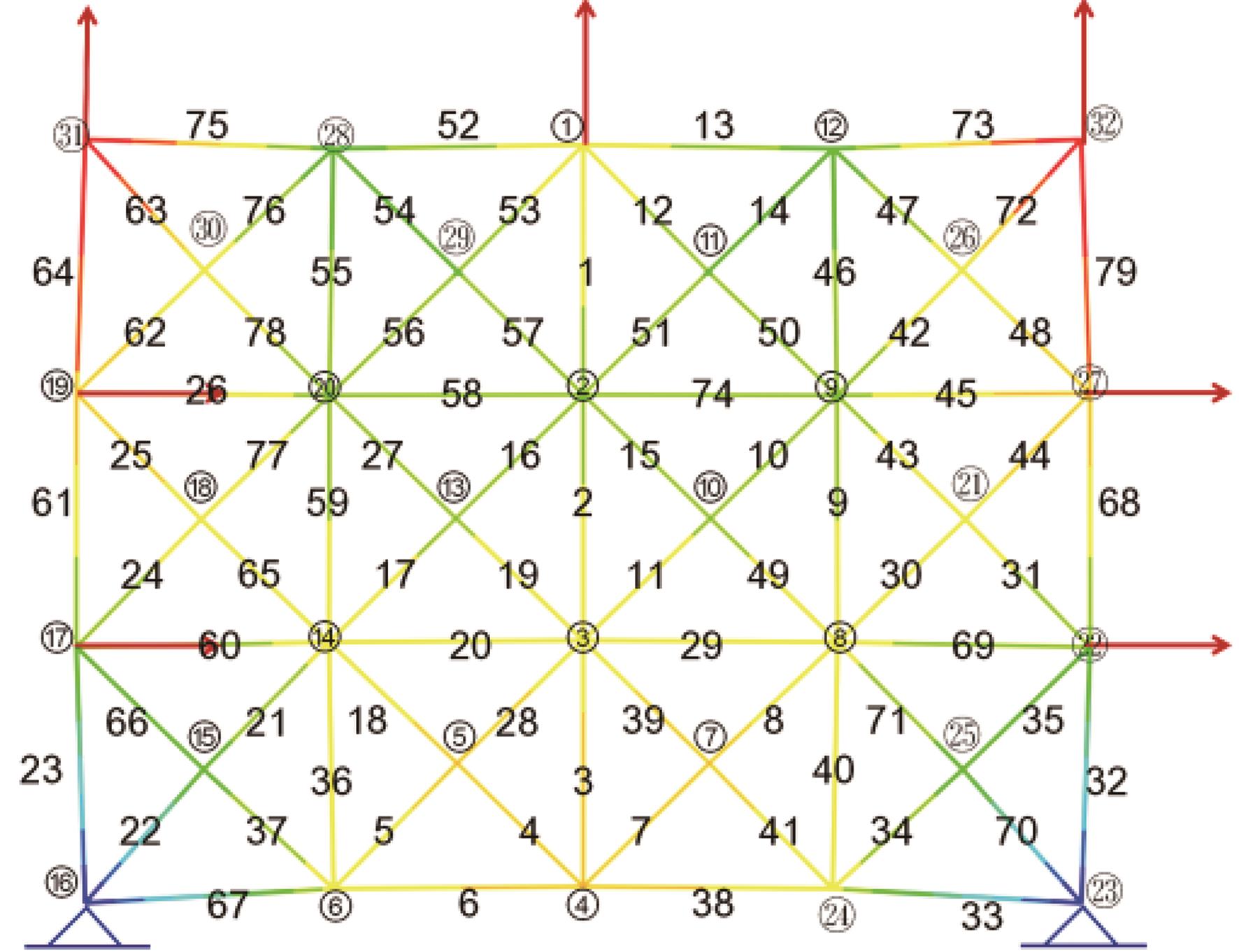
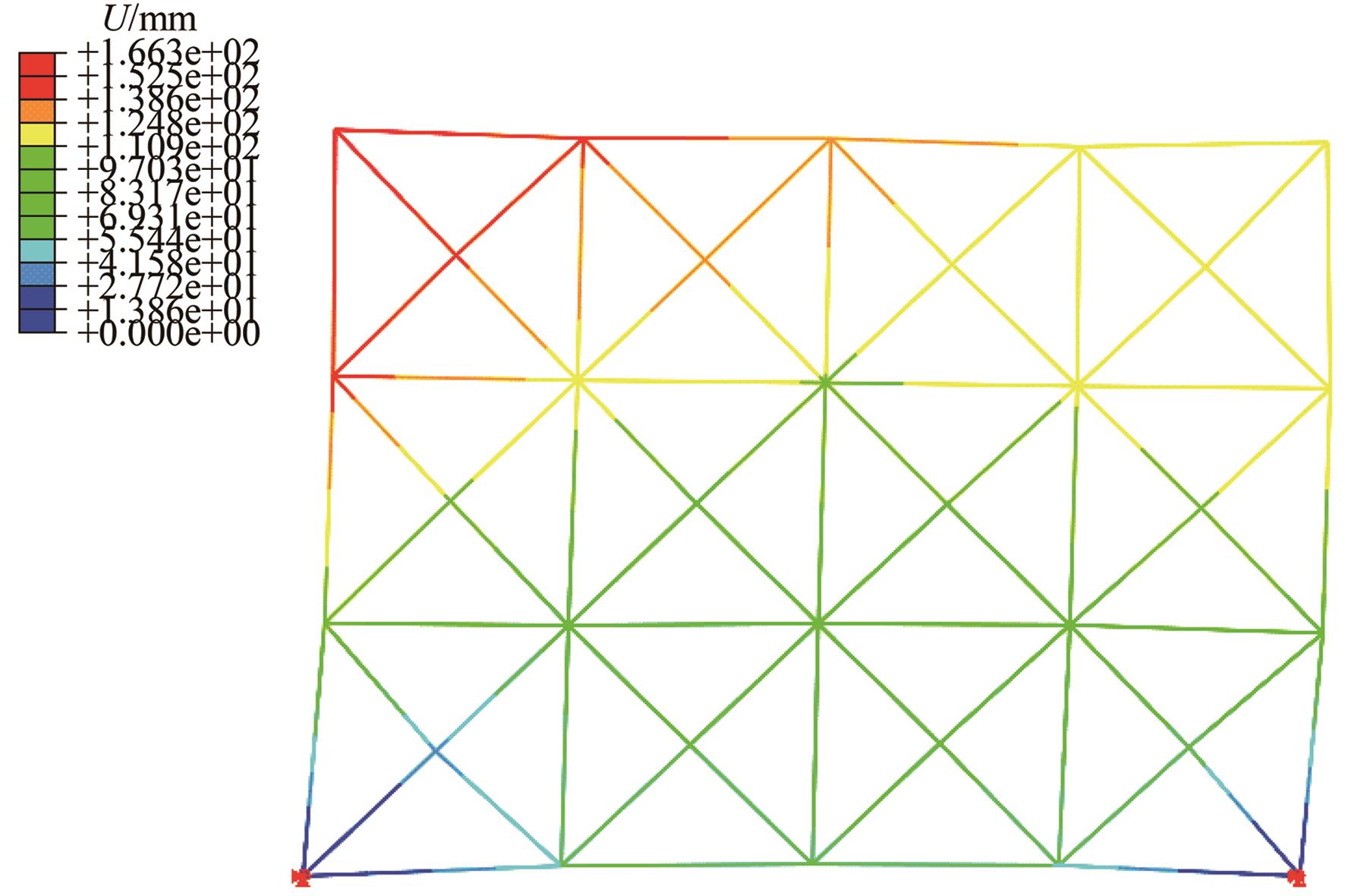
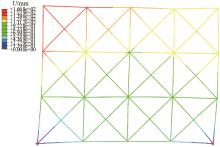
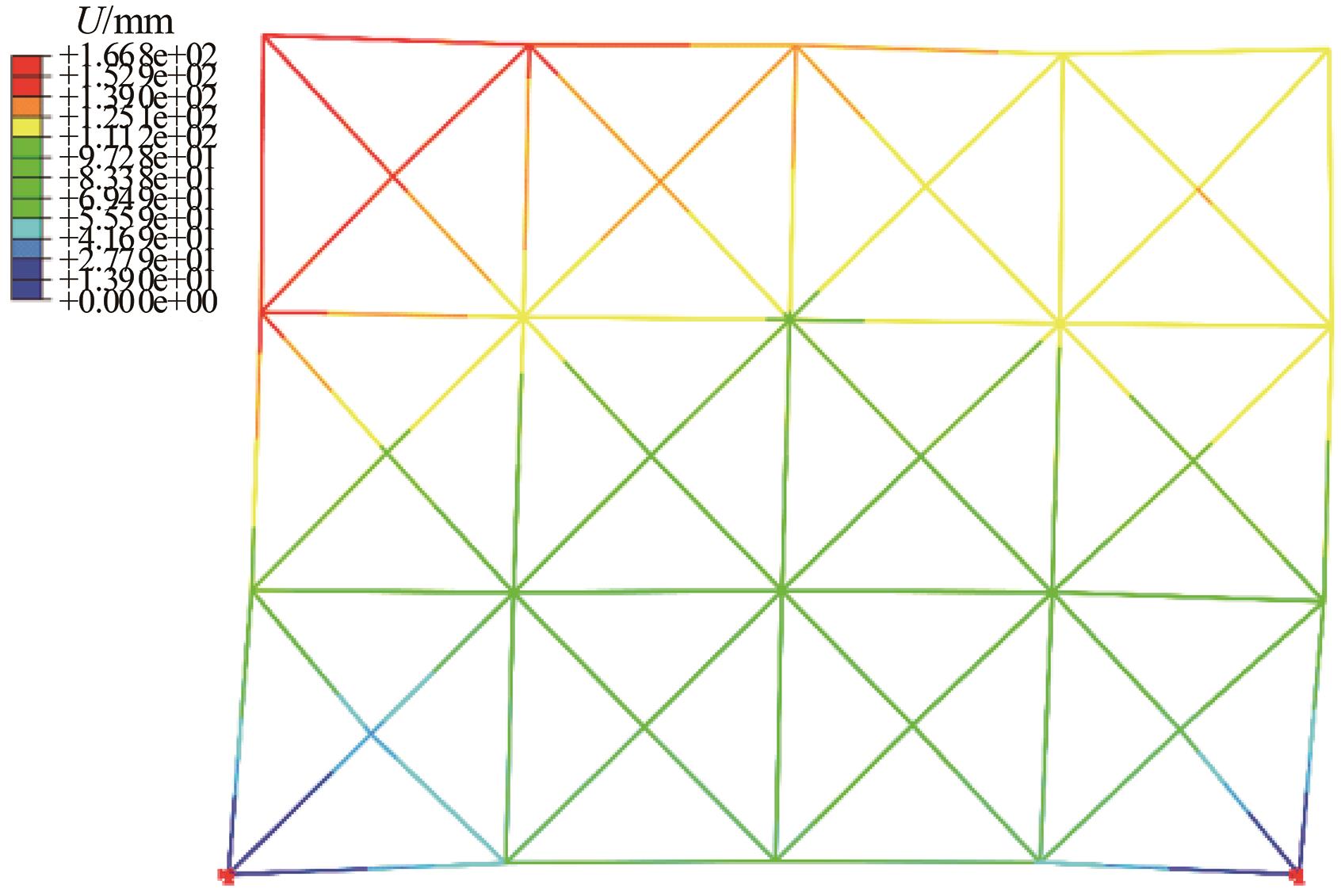
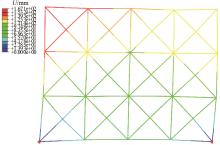
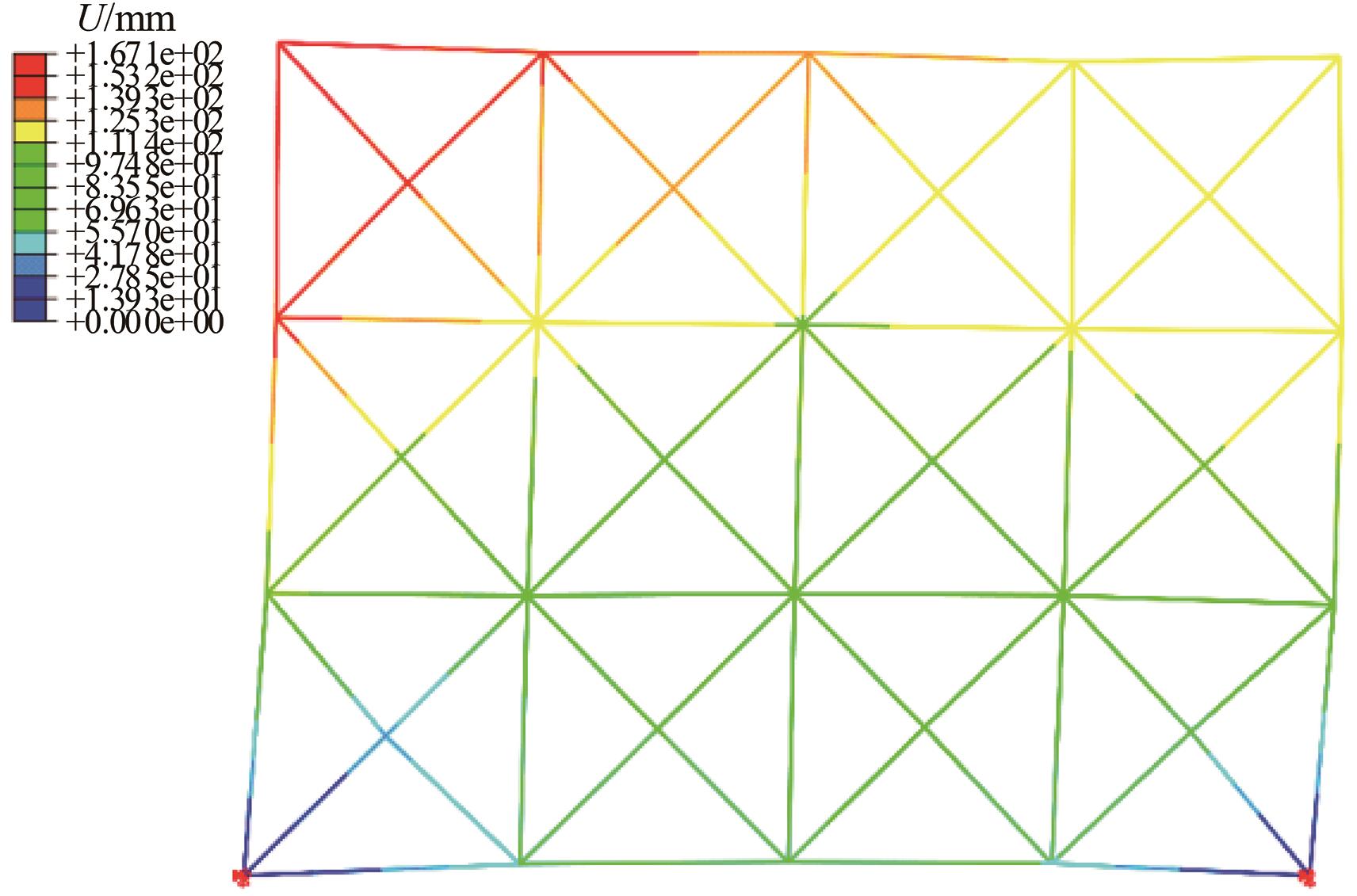
Journal of Jilin University(Engineering and Technology Edition) ›› 2025, Vol. 55 ›› Issue (1): 74-83.doi: 10.13229/j.cnki.jdxbgxb.20230333
Previous Articles Next Articles
Multi-objective optimization method of structural static displacement based on projection priority selection method
Kai MA( ),Jian-hang SUN,Sen-kang YAN,Yan TAO,Wen-tao WANG,Gui-kai GUO(
),Jian-hang SUN,Sen-kang YAN,Yan TAO,Wen-tao WANG,Gui-kai GUO( )
)
- School of Mechanical and Aerospace Engineering,Jilin University,Changchun 130022,China
CLC Number:
- O342
| 1 | 宋大同, 陈塑寰, 邱志平. 结构频率误差修正参数的最优选取问题[J]. 力学学报,1995,27(1):110-116. |
| Song Da-tong, Chen Su-huan, Qiu Zhi-ping. Optimal correction of frequency errors and selection method of parameters to be modified[J]. Acta Mechanica Sinica, 1995, 27(1):110-116. | |
| 2 | 麻凯, 管欣, 李鹏. 悬架运动学特性优化中的参数选取方法[J]. 汽车工程,2013,35(6):516-520. |
| Ma Kai, Guan Xin, Li Peng. Parameter selection method in optimization of suspension kinematics characteristics[J]. Automotive Engineering, 2013, 35(6):516-520. | |
| 3 | Conte J P, Vijalapura P K, Meghella M. Consistent finite-element response sensitivity analysis[J]. Journal of Engineering Mechanics, 2003, 129(12): 1380-1393. |
| 4 | 李莎, 肖南, 董石麟. 变长度单元自适应索杆张力结构响应灵敏度分析[J]. 华中科技大学学报:自然科学版,2014,42(10):119-123. |
| Li Sha, Xiao Nan, Dong Shi-lin. Sensitivity analysis on responses of adaptive cable-strut tensile structure with length changeable elements[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2014, 42(10):119-123. | |
| 5 | 刘广, 刘济科, 吕中荣. 基于时域响应灵敏度分析的非线性系统参数识别[J]. 振动与冲击,2018,37(21):213-219. |
| Liu Guang, Liu Ji-ke, Zhong-rong Lyu. Parametric recognition of a nonlinear system based on time domain response sensitivity analysis[J]. Journal of Vibration and Shock, 2018, 37(21):213-219. | |
| 6 | 黄毅, 刘辉, 项昌乐. 基于一、二阶嵌入灵敏度分析的车辆传动系统振动响应预测[J]. 振动与冲击,2015,34(6):72-78. |
| Huang Yi, Liu Hui, Xiang Chang-le. Vibration response prediction for a vehicle transmission system using first-order and second-order iterative embedded sensitivity analysis[J]. Journal of Vibration and Shock, 2015, 34(6):72-78. | |
| 7 | 邱志平, 王晓军. 结构灵敏度分析的区间方法[J]. 兵工学报,2005,26(6):80-84. |
| Qiu Zhi-ping, Wang Xiao-jun. An interval method for sensitivity analysis of the structures[J]. Acta Armamentarii, 2005, 26(6):80-84. | |
| 8 | Kiran R, Li L, Khandelwal K. Complex perturbation method for sensitivity analysis of nonlinear trusses [J]. Journal of Structural Engineering, 2017, 143(1): No.04016154. |
| 9 | Wang D. Sensitivity analysis of structural response to position of external applied load in plate flexural condition[J]. Computers & Structures, 2017, 190: 25-40. |
| 10 | Gu Q, Liu Y D, Li Y, et al. Finite element response sensitivity analysis of three-dimensional soil-foundation-structure interaction(SFSI) systems[J]. Earthquake Engineering and Engineering Vibration, 2018, 17(3): 555-566. |
| 11 | Lin L, Chang H, Zhang X. Research on beam structure damage identification method based on time domain response sensitivity analysis[J]. Journal of Physics: Conference Series, 2019, 1213(5):No. 052024. |
| 12 | Luo Z, Wang X, Liu D. Prediction on the static response of structures with large-scale uncertain-but-bounded parameters based on the adjoint sensitivity analysis[J]. Structural and Multidisciplinary Optimization, 2020, 61(1): 123-139. |
| 13 | 陈飙松, 张力丹, 鲁一南,等. 结构优化半解析灵敏度分析的改进算法[J]. 计算力学学报,2018,35(5):533-539. |
| Chen Biao-song, Zhang Li-dan, Lu Yi-nan, et al. Modified semi-analytical sensitivity analysis methods for structural design optimization[J]. Chinese Journal of Computational Mechanics, 2018, 35(5):533-539. | |
| 14 | Radau L, Gerzen N, Barthold F J. Sensitivity of structural response in context of linear and non-linear buckling analysis with solid shell finite elements[J]. Structural and Multidisciplinary Optimization, 2017, 55(6): 2259-2283. |
| 15 | Zuo W, Xu T, Zhang H, et al. Fast structural optimization with frequency constraints by genetic algorithm using adaptive eigenvalue reanalysis methods [J]. Structural and Multidisciplinary Optimization, 2011, 43(6): 799-810. |
| 16 | Zuo W, Yu Z, Zhao S, et al. A hybrid fox and kirsch's reduced basis method for structural static reanalysis[J]. Structural and Multidisciplinary Optimization, 2012, 46(2): 261-272. |
| 17 | Zuo W, Bai J, Yu J. Sensitivity reanalysis of static displacement using Taylor series expansion and combined approximate method[J]. Structural and Multidisciplinary Optimization, 2016, 53(5): 953-959. |
| 18 | 麻凯, 李邦辉, 杨坤, 等. 结构静态位移一阶和二阶灵敏度近似计算方法[J]. 吉林大学学报:工学版,2021,51(2):472-477. |
| Ma Kai, Li Bang-hui, Yang Kun, et al. First and second⁃order sensitivity method of structure static displacement[J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(2):472-477. |
| [1] | Jian-xiao ZHENG,Wen-bo WANG,Jin-song LIU,Li-ming ZHOU,Yu LI. Moisture-electro-mechanical coupling smoothed finite element method based on asymptotic homogenization [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(7): 1876-1886. |
| [2] | Tian-hao WANG,Bo LI,Quan-yi YU,Lin-lin XU,Guo-qiang JIA,Shan-shan GUAN. Uncertainty quantification of electric vehicle's wireless power transfer efficiency based on sparse polynomial chaos expansion method [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(12): 3433-3442. |
| [3] | Zi-rong YANG,Yan LI,Xue-feng JI,Fang LIU,Dong HAO. Sensitivity analysis of operating parameters for proton exchange membrane fuel cells [J]. Journal of Jilin University(Engineering and Technology Edition), 2022, 52(9): 1971-1981. |
| [4] | Zhong-hua SHI,Quan-wei SONG,Zhen-hang KANG,Qiang XIE,Ji-feng ZHANG. Numerical simulation and experiment on ultrasonic deicing system of airfoil structure [J]. Journal of Jilin University(Engineering and Technology Edition), 2022, 52(7): 1561-1573. |
| [5] | Kai MA,Bang-hui LI,Kun YANG,Qiao-ling LIU. First and second⁃order sensitivity method of structure static displacement [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(2): 472-477. |
| [6] | Yi JIA,Ren-da ZHAO,Yong-bao WANG,Fu-hai LI. Sensitivity analysis of viscous damper parameters for multi⁃span and long⁃unit continuous girder bridges [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(6): 1871-1883. |
| [7] | Xiao⁃qin ZHOU,Lu YANG,Lei ZHANG,Li⁃jun CHEN. Finite element analysis of hinging octahedron structure withnegative compressibility [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(3): 865-871. |
| [8] | CHEN Dong-hui, LYU Jian-hua, LONG Gang, ZHANG Yu-chen, CHANG Zhi-yong. Static rollover stability of semi-mounted agricultural machinery based on ADAMS [J]. 吉林大学学报(工学版), 2018, 48(4): 1176-1183. |
| [9] | ZHANG Ze-xing, CHEN Guo-ying, ZONG Chang-fu. Objective evaluation indices of steering performance for EPS based on sensitivity analysis [J]. 吉林大学学报(工学版), 2015, 45(4): 1043-1048. |
| [10] | KE Jun, CHENG Zhi-yong, SHI Wen-ku, SHI Teng, ZHANG Yi-jing, GUO Fu-xiang. Modal analysis and structure optimization of bus floor based on floor vibration control [J]. 吉林大学学报(工学版), 2015, 45(3): 719-725. |
| [11] | MENG Guang-wei,LI Xiao-lin,LI Feng,ZHOU Li-ming,WANG Hui. Smoothed multiscale finite element method for flow in fractured media [J]. 吉林大学学报(工学版), 2015, 45(2): 481-486. |
| [12] | CHEN Shu-ming, PENG Deng-zhi, WANG Deng-feng, LIANG Jie. Structural-acoustic coupling and optimal experimental design for automotive interior low frequency noise [J]. 吉林大学学报(工学版), 2014, 44(6): 1550-1556. |
| [13] | ZHAO Shi-jia, XU Tao, CHEN Wei, TAN Li-hui. Efficient approach for modal sensitivity analysis for near defective systems [J]. 吉林大学学报(工学版), 2013, 43(增刊1): 497-499. |
| [14] | XU Tao, QIU Bing, CHENG Fei, JIN Yan-zhong, JIANG Yong-zhou, ZHAO Shi-jia. Structural reanalysis algorithm study of topological modifications based on even lines Epsilon accelerated method [J]. 吉林大学学报(工学版), 2011, 41(增刊2): 246-249. |
| [15] | ZHANG Ying-shuang, WANG Guo-qiang, WANG Ji-xin, HOU Xiao-ting, et al. Load spectrum compiling and fatigue life prediction of wheel loader axle shaft [J]. 吉林大学学报(工学版), 2011, 41(6): 1646-1651. |
|
||