Journal of Jilin University(Engineering and Technology Edition) ›› 2020, Vol. 50 ›› Issue (5): 1739-1746.doi: 10.13229/j.cnki.jdxbgxb20190628
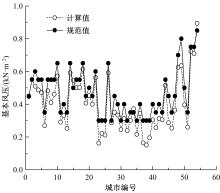
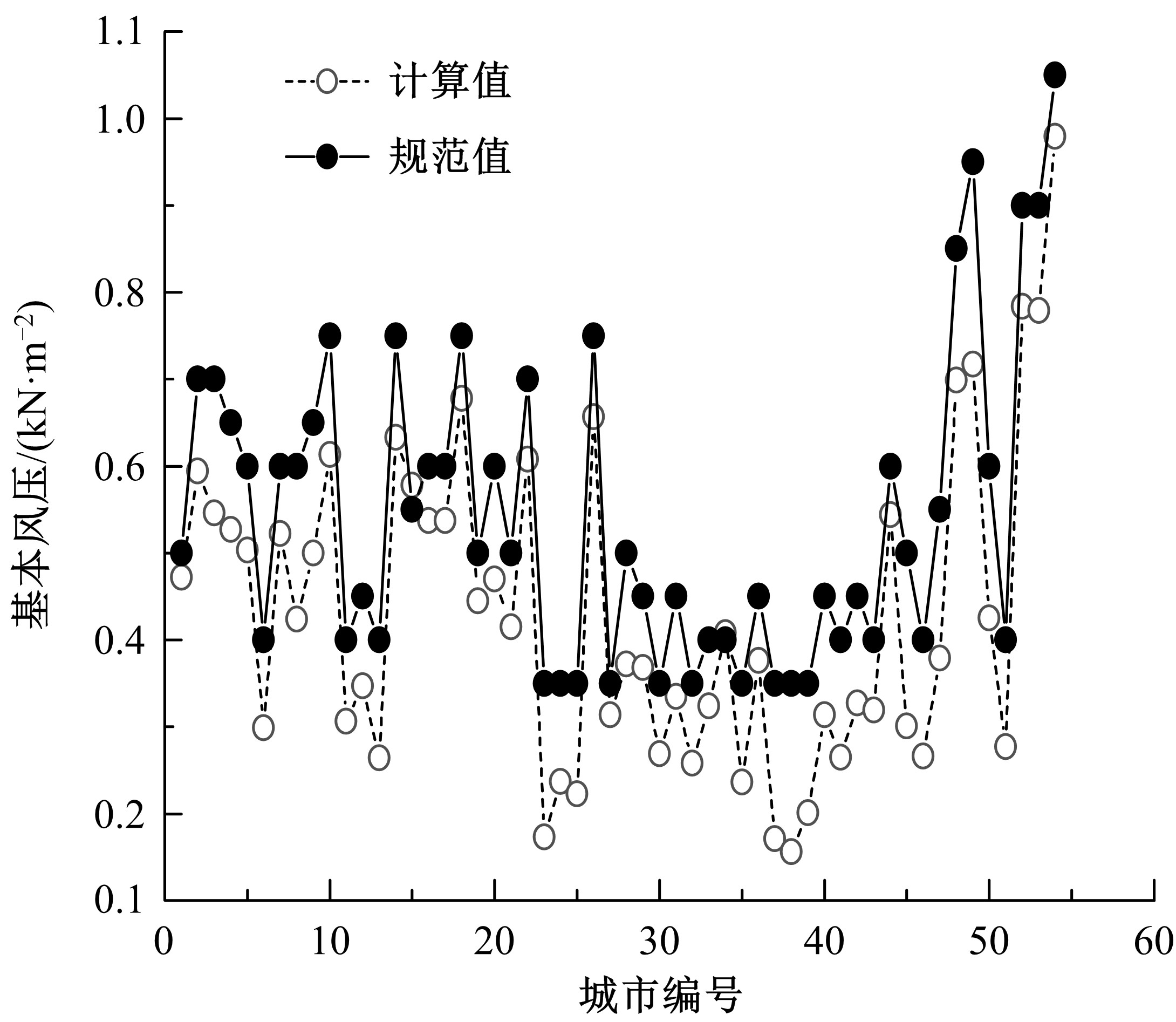
Calculation of basic wind pressure based on short⁃term wind speed data
Bo WANG1,2( ),Yuan-zheng DONG1,Li-xin DONG1
),Yuan-zheng DONG1,Li-xin DONG1
- 1.School of Civil Engineering, Jilin Jianzhu University, Changchun 130118, China
2.Jilin Structural and Earthquake Resistance Technology Innovation Center, Changchun 130118, China
CLC Number:
- TU312
| 1 | Wang B, Etheridge D W, Ohba M. Wind tunnel investigation of natural ventilation through multiple stacks. Part 1: mean values[J]. Building & Environment, 2011, 46(7): 1380-1392. |
| 2 | GB50009—2012. 建筑结构荷载规范[S]. |
| 3 | Mircea G. Estimation of extreme wind from short records[J]. Journal of the Structural Division, 1982, 108(5): 1034-1048. |
| 4 | 陈朝辉, 管前乾. 基于短期资料的重庆风速极值渐进分布分析[J]. 重庆大学学报: 自然科学版, 2006, 29(12): 88-92. |
| Chen Zhao-hui, Guan Qian-qian. Simulating of asymptotic distributions of extreme wind speed in Chongqing using short-term wind speed records[J]. Journal of Chongqing University(Natural Science Edition), 2006, 29(12): 88-92. | |
| 5 | 罗乃东. 基于可靠度的高层、高耸结构抗风分析[D]. 大连: 大连理工大学土木工程学院, 2002. |
| Luo Nai-dong. Study of wind-resistant of tall building base on reliability theory[D]. Dalian: School of Civil Engineering, Dalian University of Technology, 2002. | |
| 6 | Lee B H, Ahn D J, Kim H G, et al. An estimation of the extreme wind speed using the Korea wind map[J]. Renewable Energy, 2012, 42: 4-10. |
| 7 | 孟庆珍, 唐谟智. 成都地面气温与风速年极大值的渐近分布及参数估计[J]. 成都气象学院学报, 1997, 12(4): 284-291. |
| Meng Qing-zhen, Tang Mo-zhi. On asymptotic distribution of yearly maximum values of surface temperature and wind speed over Chengdu and the estimation of their parameters[J]. Journal of Chengdu Institute of Meteorology, 1997, 12(4): 284-291. | |
| 8 | Harris I. Generalised pareto methods for wind extremes. Useful tool or mathematical mirage?[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2005, 93(5): 341-360. |
| 9 | Galambos J. The Cassical Extreme Value Model: Mathematical Results Versus Statistical Inference[M]. New York: Statistics for the 21st Century, 2000: 173-187. |
| 10 | Elahi A S, Ghoranneviss M, Emami M. Comparative measurements of plasma position using multipole moments method and analytical solution of grad-shafranov equation in IR-T1 tokamak[J]. Journal of Fusion Energy, 2009, 28(4): 385-389. |
| 11 | 张勇. 基本风压、雪压统计分析与荷载组合系数研究[D]. 沈阳: 沈阳建筑大学土木工程学院, 2011. |
| Zhang Yong. Statistical analysis about basic wind and snow pressure and research about load combinatorial coefficient[D]. Shenyang: School of Civil Engineering, Shenyang University of Architecture, 2011 | |
| 12 | 段忠东, 周道成. 极值概率分布参数估计方法的比较研究[J]. 哈尔滨工业大学学报, 2004, 36(12): 1605-1609. |
| Duan Zhong-dong, Zhou Dao-cheng. A comparative study on parameter estimate method for extremal value distribution[J]. Journal of Harbin Institute of Technology, 2004, 36(12): 1605-1609. | |
| 13 | 康朝杰, 杜文风, 杨雪. 基于极大似然法的雪荷载计算与分析[J]. 河南大学学报: 自然科学版, 2016, 46(2): 220-225. |
| Kang Chao-jie, Du Wen-feng, Yang Xue, et al. Calculation and analysis of snow loads based on the maximum likelihood method[J]. Journal of Henan University(Natural Science), 2016, 46(2): 220-225. | |
| 14 | Zhang C L, Fan J H. An X-ray luminosity analysis for FRIs and FRIIs[J]. Science in China Series G Physics Mechanics and Astronomy, 2009, 52(9): 1434-1441. |
| 15 | 方晓, 张运福, 房一禾. 辽宁省沿海地区极值风速概率分布特征[J]. 现代农业科技, 2015(22): 256-257, 259. |
| Fang Xiao, Zhang Yun-fu, Fang Yi-he. Characteristic of probability distribution of extreme wind speeds in coast area of Liaoning province[J]. XianDai NongYe KeJi, 2015(22): 256-257, 259. | |
| 16 | 叶征伟. 山区高墩大跨连续刚构桥风环境及风荷载研究[D]. 杭州: 浙江大学建筑工程学院, 2012. |
| Ye Zheng-wei. Study on the wind-environment and wind loads of the long-span continuous rigid frame bridge with tall piers in mountainous areas[D]. Hangzhou: College of Civil Engineering and Architecture, Zhejiang University, 2012. | |
| 17 | 屠其璞. 气象应用概率统计学[M]. 北京: 气象出版社, 1984. |
| 18 | 王卫锋, 颜全胜, 李立军, 等. 大跨度斜拉桥侧风非线性分析[J]. 吉林大学学报: 工学版, 2007, 37(4): 786-789. |
| Wang Wei-feng, Yan Quan-sheng, Li Li-jun, et al. Nonlinear analysis for a long span cable stayed bridge under lateral wind loads[J]. Journal of Jilin University(Engineering and Technology Edition), 2007, 37(4): 786-789. | |
| 19 | 姜浩, 郭学东, 张艳辉. 基于时域分析的风载激励下桥梁结构动力特性识别[J]. 吉林大学学报: 工学版, 2011,41(5): 1279-1283. |
| Jiang Hao, Guo Xue-dong, Zhang Yan-hui. Dynamic behavior identification of concrete bridge structure under wind load excitation based on time-domain analysis[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(5): 1279-1283. |
| [1] | Su-duo XUE,Jian LU,Xiong-yan LI,Ren-jie LIU. Influence of grid⁃jumping arrangement on static and dynamic performance of annular crossed cable⁃truss structure [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(5): 1687-1697. |
| [2] | Ming LI,Hao-ran WANG,Wei-jian ZHAO. Experimental of loading-bearing capacity of one-way laminated slab with shear keys [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(2): 654-667. |
| [3] | Peng-hui WANG,Hong-xia QIAO,Qiong FENG,Hui CAO,Shao-yong WEN. Durability model of magnesium oxychloride-coated reinforced concrete under the two coupling factors [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(1): 191-201. |
| [4] | Ming LI,Hao-ran WANG,Wei-jian ZHAO. Mechanical properties of laminated slab with shear keys [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(5): 1509-1520. |
| [5] | Jun ZHANG,Cheng QIAN,Chun⁃yan GUO,Yu⁃jun QIAN. Dynamic design of building livability based on multi⁃source spatiotemporal data [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(4): 1169-1173. |
| [6] | Ning⁃hui LIANG,Qing⁃xu MIAO,Xin⁃rong LIU,Ji⁃fei DAI,Zu⁃liang ZHONG. Determination of fracture toughness and softening traction⁃separation law of polypropylene fiber reinforced concrete [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(4): 1144-1152. |
| [7] | Lei ZHANG,Bao⁃guo LIU,Zhao⁃fei CHU. Model test of the influence on shield shaft owing to water loss settlement of deep sandstone aquifer layer [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(3): 788-797. |
| [8] | ZHENG Yi-feng, ZHAO Qun, BAO Wei, LI Zhuang, YU Xiao-fei. Wind resistance performance of long-span continuous rigid-frame bridge in cantilever construction stage [J]. 吉林大学学报(工学版), 2018, 48(2): 466-472. |
| [9] | NI Ying-sheng, SUN Qi-xin, MA Ye, XU Dong. Calculation of capacity reinforcement about composite box girder with corrugated steel webs based on tensile stress region theory [J]. 吉林大学学报(工学版), 2018, 48(1): 148-158. |
| [10] | WANG Teng, ZHOU Ming-ru, MA Lian-sheng, QIAO Hong-xia. Fracture grouting crack growth of collapsible loess based on fracture theory [J]. 吉林大学学报(工学版), 2017, 47(5): 1472-1481. |
| [11] | ZHENG Yi-feng, MAO Jian, LIANG Shi-zhong, ZHENG Chuan-feng. Negative skin friction of pile foundation considering soil consolidation in high fill site [J]. 吉林大学学报(工学版), 2017, 47(4): 1075-1081. |
| [12] | LI Jing, WANG Zhe. Mechanical characteristics of concrete under true triaxial loading condition [J]. 吉林大学学报(工学版), 2017, 47(3): 771-777. |
| [13] | GUO Nan, ZHANG Ping-yang, ZUO Yu, ZUO Hong-liang. Bending performance of glue-lumber beam reinforced by bamboo plyboard [J]. 吉林大学学报(工学版), 2017, 47(3): 778-788. |
| [14] | ZHANG Jing, LIU Xiang-dong. Prediction of concrete strength based on least square support vector machine optimized by chaotic particle swarm optimization [J]. 吉林大学学报(工学版), 2016, 46(4): 1097-1102. |
| [15] | GUO Xue-dong, MA Li-jun, ZHANG Yun-long. Analytical solution of the double joint layer composite beam with shear-slip under vertical concentrated load [J]. 吉林大学学报(工学版), 2016, 46(2): 432-438. |
|
||