Journal of Jilin University(Engineering and Technology Edition) ›› 2021, Vol. 51 ›› Issue (1): 217-224.doi: 10.13229/j.cnki.jdxbgxb20190867

Previous Articles    

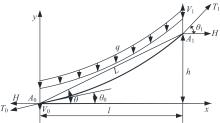
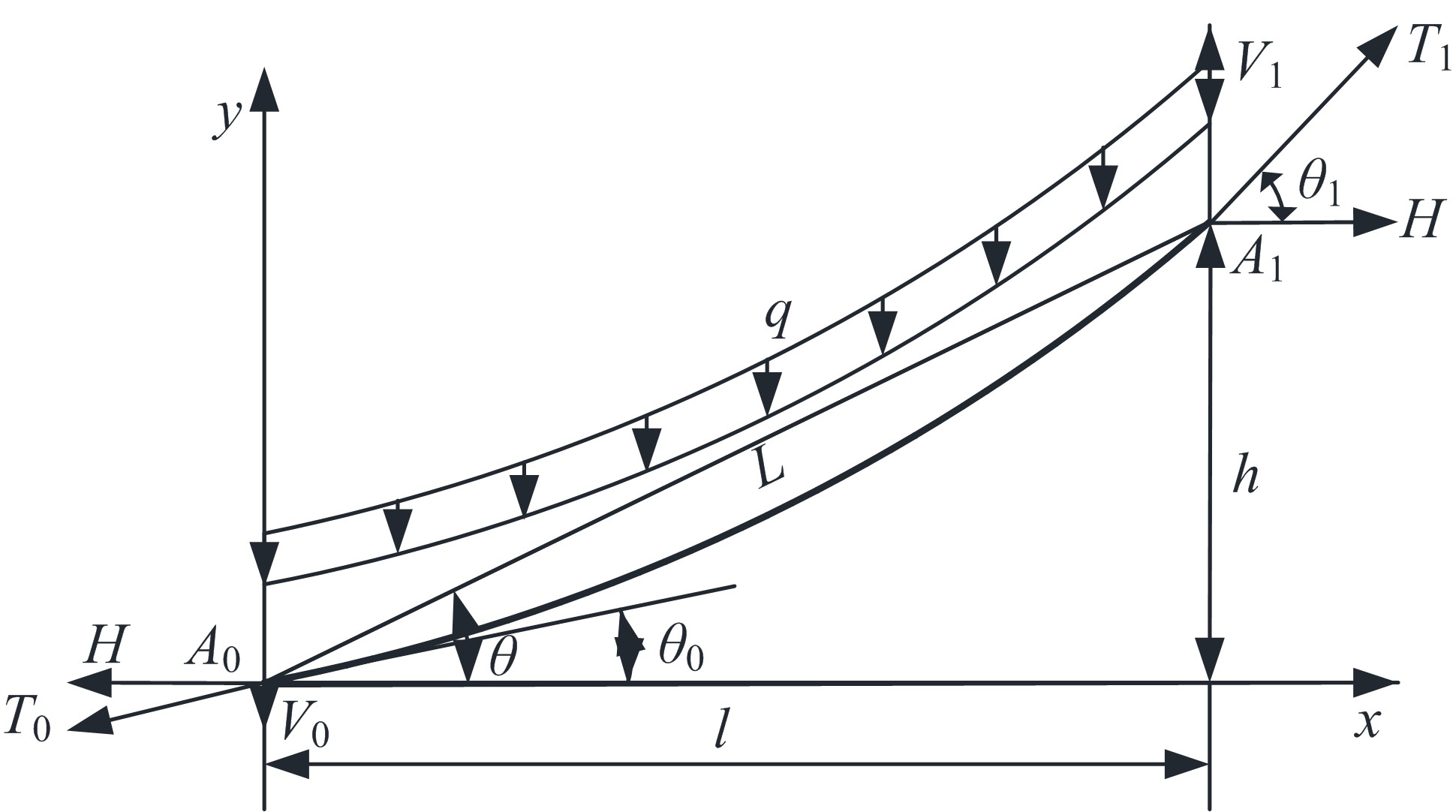
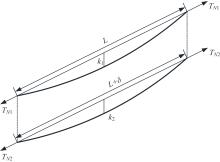
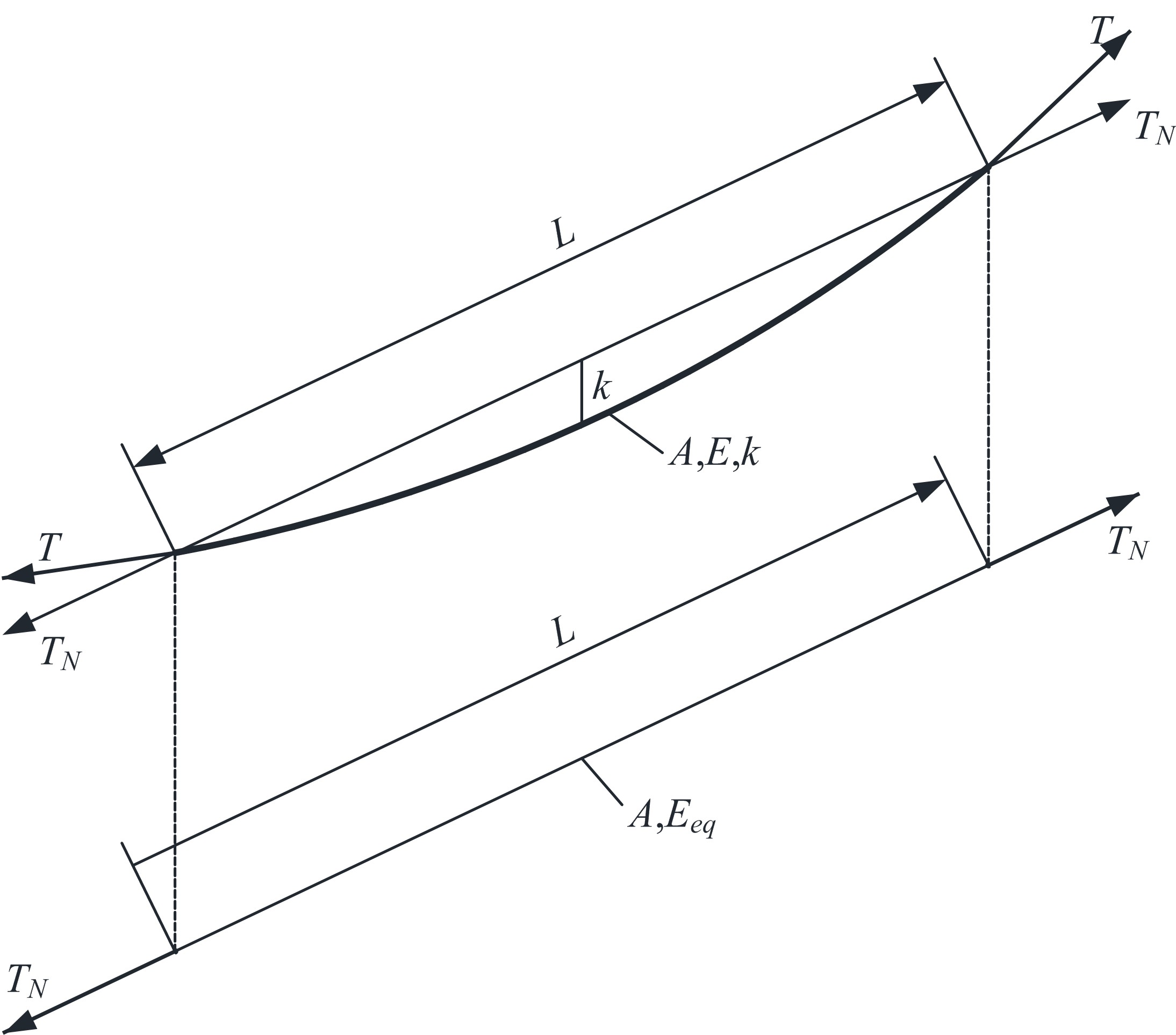
Analytical method for elongation of stayed-cable with catenary configuration

De-shan SHAN(),Xiao ZHANG,Xiao-yu GU,Qiao LI   

  1. School of Civil Engineering，Southwest Jiaotong University，Chengdu 610031，China
  • Received:2019-09-05 Online:2021-01-01 Published:2021-01-20

RICH HTML

 22   

PDF (PC)

712

Abstract:

In order to meet the requirements of unstressed length and elongation control for stay cable during its installation， the analytical method for calculating the elongation of the stay cable with catenary configuration is discussed. First， the geometric equation of the stay cable with catenary configuration is obtained by applying the force equilibrium condition to the stay cable， and the analytical expressions of the cable length and its elongation under a certain given cable tension are acquired by direct integration. Moreover， the analytical expressions of the cable elongation under varying cable tension are obtained by using the deformation coordination condition. Then， the equivalent elastic modulus for stay cable with catenary configuration is discussed based on strain equivalence. It is verified that the equivalent elastic modulus for the stay cable with catenary configuration can be simplified to the equivalent elastic modulus for the stay cable with parabolic configuration. Taking the real parameters of the stay cables of a certain cable-stayed bridge with composite/hybrid girder as the case study， the analytical expressions of stay cable length and its corresponding elongation under a given cable tension are verified by numerical integration and simplified formulas respectively. Furthermore， the analytical expressions for the elongation of stay cable with varying cable tension are verified by the Nlabs finite element and equivalent elastic modulus method. The results show that the proposed analytical expressions can simply and directly figure out the exact elongation of stay cable， which provide the theory and straight forward method for the unstressed length of stay cable and the elongation control of stay cable during its installation.

Key words: civil engineering, stay cable, catenary configuration, elongation, parabolic configuration

CLC Number: 

  • U448

Fig.1

Coordinate system of stay cable"

Fig.2

Stay cable deformation under cable tensions TN1and TN2"

Fig.3

Surrogate straight rod with equivalent elastic modulus"

Fig.4

Approximate calculation of Esec for initial tension of stay cable"

Fig.5

Number of stay cable"

Table 1

Parameters of stay cables"

索号钢束规格索长/m索号钢束规格索长/m
ZN1M250?4395.218BN1M250?4395.740
ZN2M250?37102.747BN2M250?37103.637
ZN3M250?37110.259BN3M250?37111.484
ZN4M250?37118.312BN4M250?37119.840
ZN5M250?43126.783BN5M250?43128.574
ZN6M250?43135.787BN6M250?43137.801
ZN7M250?43146.672BN7M250?50148.888
ZN8M250?50157.413BN8M250?50159.813
ZN9M250?50168.569BN9M250?55171.135
ZN10M250?50180.101BN10M250?55182.817
ZN11M250?55191.881BN11M250?55194.731
ZN12M250?61203.900BN12M250?55206.865
ZN13M250?61216.121BN13M250?61219.185
ZN14M250?61228.512BN14M250?61231.650
ZN15M250?73241.047BN15M250?61244.267
ZN16M250?73253.706BN16M250?61256.987
ZN17M250?73266.474BN17M250?73269.806
ZN18M250?73279.331BN18M250?73282.707
ZN19M250?73292.271BN19M250?85296.683
ZN20M250?73305.283BN20M250?85308.723
ZN21M250?85318.358BN21M250?85313.023
ZS1M250?3791.274BS1M250?5596.099
ZS2M250?3799.436BS2M250?55103.565
ZS3M250?37107.445BS3M250?55110.055
ZS4M250?37115.793BS4M250?55116.216
ZS5M250?43124.395BS5M250?61122.024
ZS6M250?43133.479BS6M250?61127.999
ZS7M250?43144.144BS7M250?61135.001
ZS8M250?50154.718BS8M250?61141.864
ZS9M250-50165.734BS9M250?73149.004
ZS10M250?50177.157BS10M250?73156.412
ZS11M250?55188.836BS11M250?73164.000
ZS12M250?55200.770BS12M250?73171.770
ZS13M250?55212.918BS13M250?73179.732
ZS14M250?61225.246BS14M250?73187.799
ZS15M250?61237.727BS15M250?73196.987
ZS16M250?61250.338BS16M250?73204.283
ZS17M250?73263.062BS17M250?73212.623
ZS18M250?73275.885BS18M250?73221.184
ZS19M250?73288.792BS19M250?85229.732
ZS20M250?73301.775BS20M250?85238.348

Fig.6

Comparison of third tensile elongation of cable by different algorithms（unit: mm）"

Fig.7

Comparison of second tensile elongation increment of cable（unit:mm）"

Fig.8

Comparison of third tensile elongation increment of cable（unit:mm）"

1 Li H, Zhang F, Jin Y. Real-time identification of time-varying tension in stay cables by monitoring cable transversal acceleration[J]. Structural Control and Health Monitoring, 2014, 21(7): 1100-1117.
2 An Y, Zhong Y, Tan Y, et al. Experimental and numerical studies on a test method for damage diagnosis of stay cables[J]. Advances in Structural Engineering, 2017, 20(2): 245-256.
3 Gimsing N J, Georgakis C T. Cable Supported Bridges-Concept and Design[M]. 3rd ed. Chichester, West Sussex, United Kingdom: John Wiley & Sons Ltd, 2012.
4 李乔, 卜一之, 张清华. 大跨度斜拉桥施工全过程几何控制概论与应用[M]. 成都:西南交通大学出版社, 2009.
5 Wu J, Frangopol D M, Soliman M. Geometry control simulation for long-span steel cable-stayed bridges based on geometrically nonlinear analysis[J]. Engineering Structures, 2015, 90: 71-82.
6 Ernst H J. The E-Module of rope with consideration of the dip[J]. The Civil Engineering, 1965, 40(1): 52-55.
7 Hajdin N, Michaltsos G T, Konstantakopoulos T G. About the equivalent modulus of elasticity of cables of cable-stayed bridges[J]. The Scientific Journal Facta Universitatis, 1998, 11(5): 569-575.
8 郝超, 裴岷山, 强士中. 大跨度斜拉桥拉索无应力长度的计算方法比较[J]. 重庆交通学院学报, 2001, 20(3): 1-3.
Hao Chao, Pei Min-shan, Qiang Shi-zhong. Comparison of algorithm for calculating non-stress length of cable in long-span cable-stayed bridges[J]. Journal of Chongqing Jiaotong University, 2001, 20(3): 1-3.
9 任淑琰, 顾明. 斜拉桥拉索静力构形分析[J]. 同济大学学报:自然科学版, 2005, 33(5): 595-599.
Ren Shu-yan, Gu Ming. Static analysis of cables' configuration in cable-Stayed bridges[J]. Journal of Tongji University(Natural Science Edition), 2005, 33(5): 595-599.
10 杨佑发, 白文轩, 郜建人. 悬链线解答在斜拉索数值分析的应用[J]. 重庆建筑大学学报, 2007, 29(6): 31-34.
Yang You-fa, Bai Wen-xuan, Gao Jian-ren. Application of Catenary Solution in numerical analysis of stay cables[J]. Journal of Chongqing University of Architecture, 2007, 29(6): 31-34.
11 李乔, 周凌远. 桥梁结构非线性分析系统NLABS使用说明书[M]. 成都:西南交通大学出版社, 2019.
12 Wu Z, Wei J. Nonlinear analysis of spatial cable of long-span cable-stayed bridge considering rigid connection[J]. KSCE Journal of Civil Engineering, 2019, 23(5): 2148-2157.
13 梁鹏, 肖汝诚, 孙斌. 超大跨度斜拉桥几何非线性精细化分析[J]. 中国公路学报, 2007, 20(2): 57-62.
Liang Peng, Xiao Ru-cheng, Sun Bin. Refined geometrical nonlinear analysis for super-long-span cable-stayed bridge[J]. China Journal of Highway and Transport, 2007, 20(2): 57-62.
14 汪峰, 刘沐宇. 斜拉桥无应力索长的精确求解方法[J]. 华中科技大学学报:自然科学版, 2010, 38(7): 54-57.
Wang Feng, Liu Mu-yu. An accurate method for determining unstressed cable length in long span cable stayed bridge[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2010, 38(7): 54-57.
15 苑仁安, 秦顺全. 无应力状态法在钢绞线斜拉索施工中的应用[J]. 桥梁建设, 2012, 42(3): 75-79.
Yuan Ren-an, Qin Shun-quan. Application of unstressed state method to construction of steel strand stay cable[J]. Bridge Construction, 2012, 42(3): 75-79.
16 Kumarasena S, Jones N P, Irwin P, et al. Wind-induced vibration of stay cables[R]. Washington DC:United States Department of Transportation, 2007: 213-217.
17 孟庆成, 齐欣, 李乔, 等. 千米级斜拉桥斜拉索相关参数计算方法[J]. 桥梁建设, 2009(2): 58-60, 75.
Meng Qing-cheng, Qi Xin, Li Qiao, et al. Algorithm for relevant parameters of stay cables of cable-stayed bridge with span length of 1 000-m scale[J]. Bridge Construction, 2009(2): 58-60, 75.
18 Vairo G. A closed-form refined model of the cables' nonlinear response in cable-stayed structures[J]. Mechanics of Advanced Materials and Structures, 2009, 16(6): 456-466.
[1] Su-duo XUE,Jian LU,Xiong-yan LI,Ren-jie LIU. Influence of grid⁃jumping arrangement on static and dynamic performance of annular crossed cable⁃truss structure [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(5): 1687-1697.
[2] Bo WANG,Yuan-zheng DONG,Li-xin DONG. Calculation of basic wind pressure based on short⁃term wind speed data [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(5): 1739-1746.
[3] Ming LI,Hao-ran WANG,Wei-jian ZHAO. Experimental of loading-bearing capacity of one-way laminated slab with shear keys [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(2): 654-667.
[4] Peng-hui WANG,Hong-xia QIAO,Qiong FENG,Hui CAO,Shao-yong WEN. Durability model of magnesium oxychloride-coated reinforced concrete under the two coupling factors [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(1): 191-201.
[5] Ming LI,Hao-ran WANG,Wei-jian ZHAO. Mechanical properties of laminated slab with shear keys [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(5): 1509-1520.
[6] Jun ZHANG,Cheng QIAN,Chun⁃yan GUO,Yu⁃jun QIAN. Dynamic design of building livability based on multi⁃source spatiotemporal data [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(4): 1169-1173.
[7] Ning⁃hui LIANG,Qing⁃xu MIAO,Xin⁃rong LIU,Ji⁃fei DAI,Zu⁃liang ZHONG. Determination of fracture toughness and softening traction⁃separation law of polypropylene fiber reinforced concrete [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(4): 1144-1152.
[8] Lei ZHANG,Bao⁃guo LIU,Zhao⁃fei CHU. Model test of the influence on shield shaft owing to water loss settlement of deep sandstone aquifer layer [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(3): 788-797.
[9] ZHENG Yi-feng, ZHAO Qun, BAO Wei, LI Zhuang, YU Xiao-fei. Wind resistance performance of long-span continuous rigid-frame bridge in cantilever construction stage [J]. 吉林大学学报(工学版), 2018, 48(2): 466-472.
[10] NI Ying-sheng, SUN Qi-xin, MA Ye, XU Dong. Calculation of capacity reinforcement about composite box girder with corrugated steel webs based on tensile stress region theory [J]. 吉林大学学报(工学版), 2018, 48(1): 148-158.
[11] WANG Teng, ZHOU Ming-ru, MA Lian-sheng, QIAO Hong-xia. Fracture grouting crack growth of collapsible loess based on fracture theory [J]. 吉林大学学报(工学版), 2017, 47(5): 1472-1481.
[12] ZHENG Yi-feng, MAO Jian, LIANG Shi-zhong, ZHENG Chuan-feng. Negative skin friction of pile foundation considering soil consolidation in high fill site [J]. 吉林大学学报(工学版), 2017, 47(4): 1075-1081.
[13] LI Jing, WANG Zhe. Mechanical characteristics of concrete under true triaxial loading condition [J]. 吉林大学学报(工学版), 2017, 47(3): 771-777.
[14] GUO Nan, ZHANG Ping-yang, ZUO Yu, ZUO Hong-liang. Bending performance of glue-lumber beam reinforced by bamboo plyboard [J]. 吉林大学学报(工学版), 2017, 47(3): 778-788.
[15] ZHANG Jing, LIU Xiang-dong. Prediction of concrete strength based on least square support vector machine optimized by chaotic particle swarm optimization [J]. 吉林大学学报(工学版), 2016, 46(4): 1097-1102.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
Copyright © Journal of Jilin University(Engineering and Technology Edition), All Rights Reserved.
Tel: +86-431-85095297　Fax: +86-431-85094074　E-mail: xbgxb@jlu.edu.cn
Powered by Beijing Magtech Co. Ltd