Journal of Jilin University(Engineering and Technology Edition) ›› 2024, Vol. 54 ›› Issue (4): 902-916.doi: 10.13229/j.cnki.jdxbgxb.20221637

Previous Articles     Next Articles

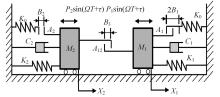
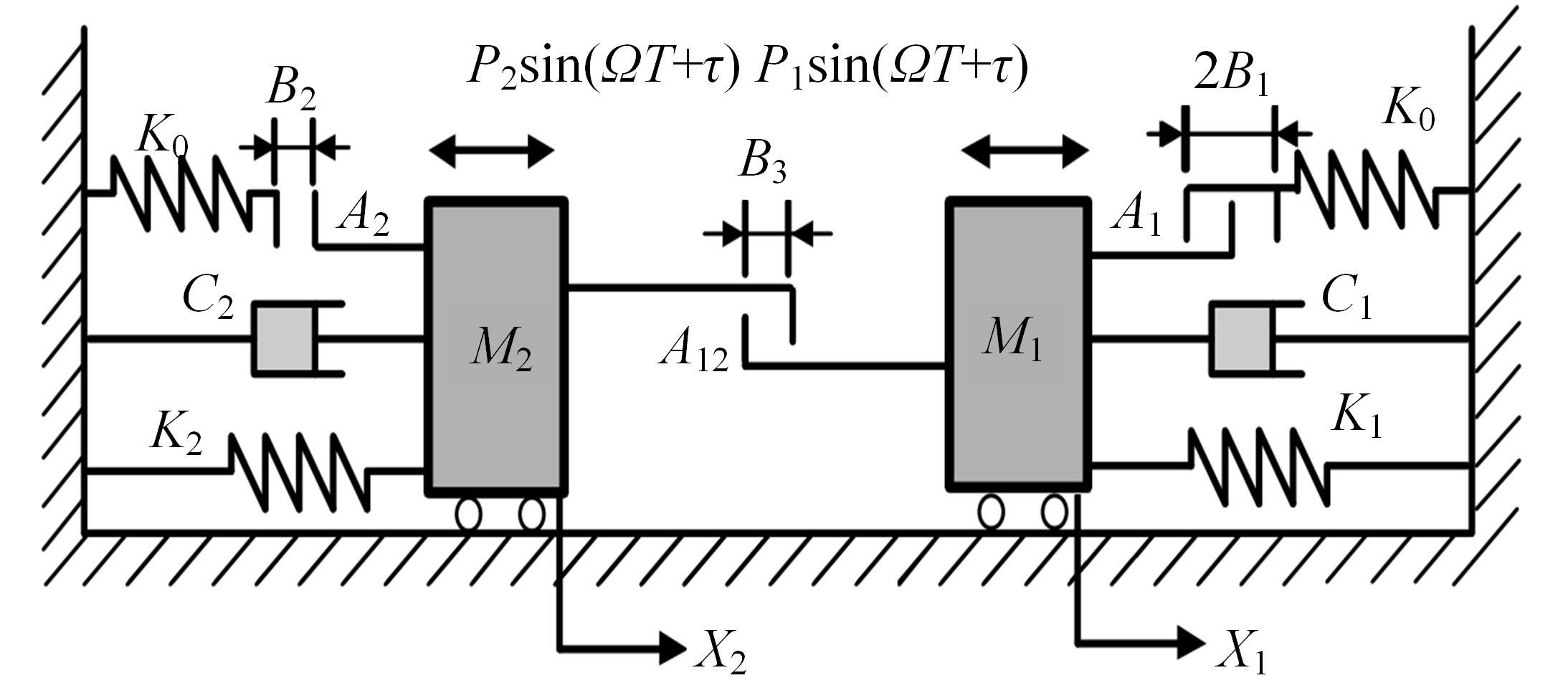
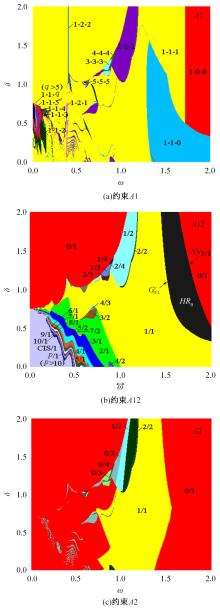
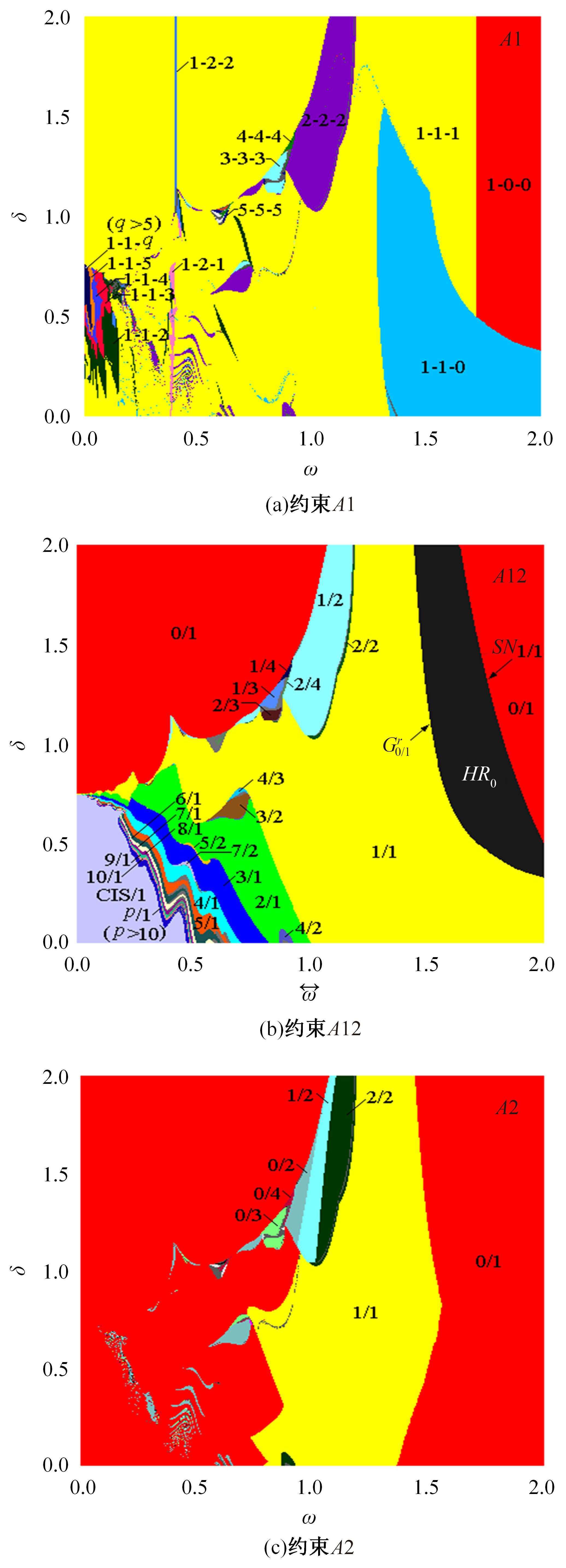
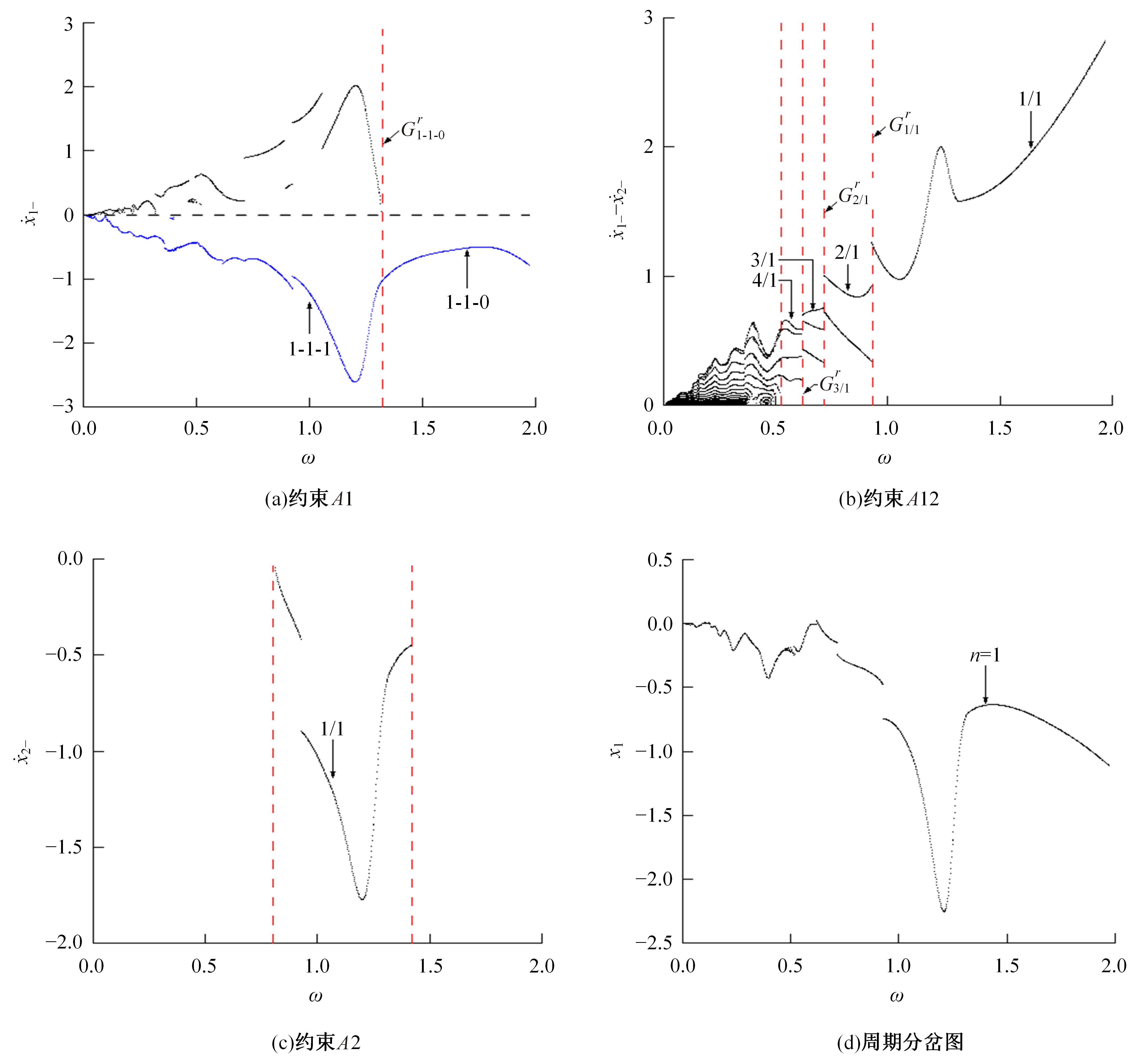
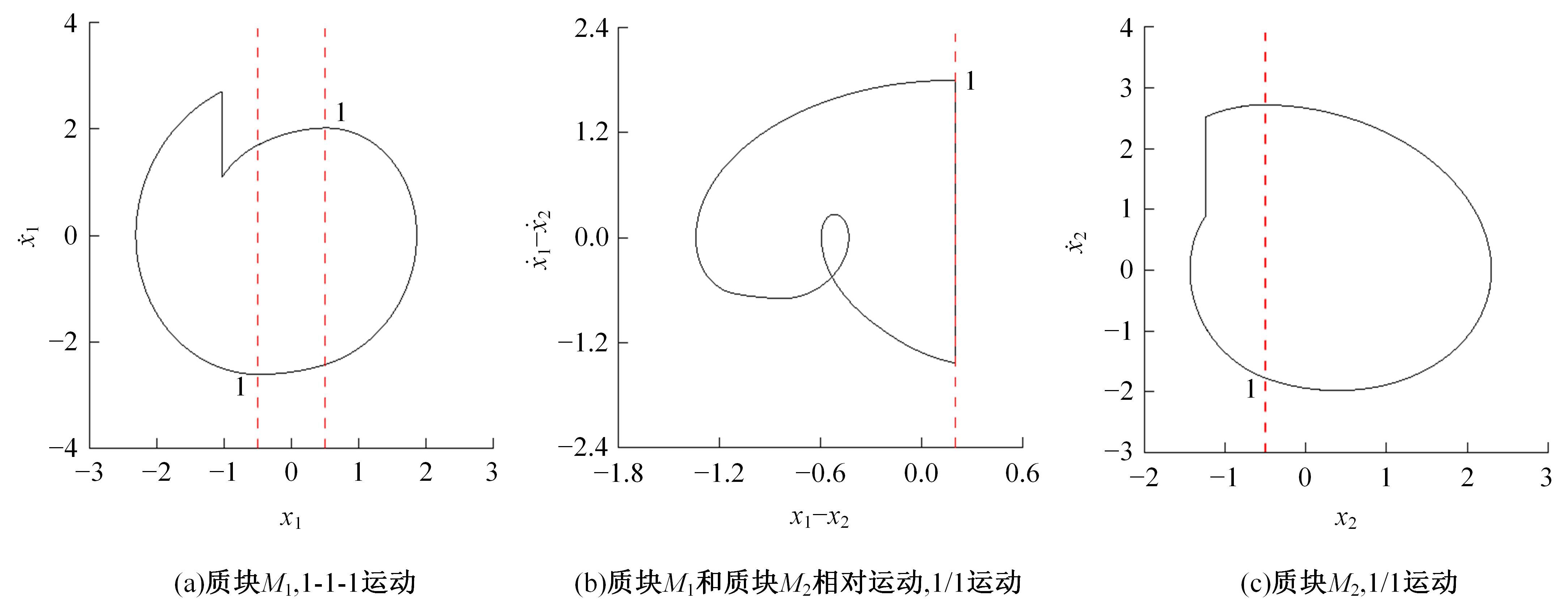
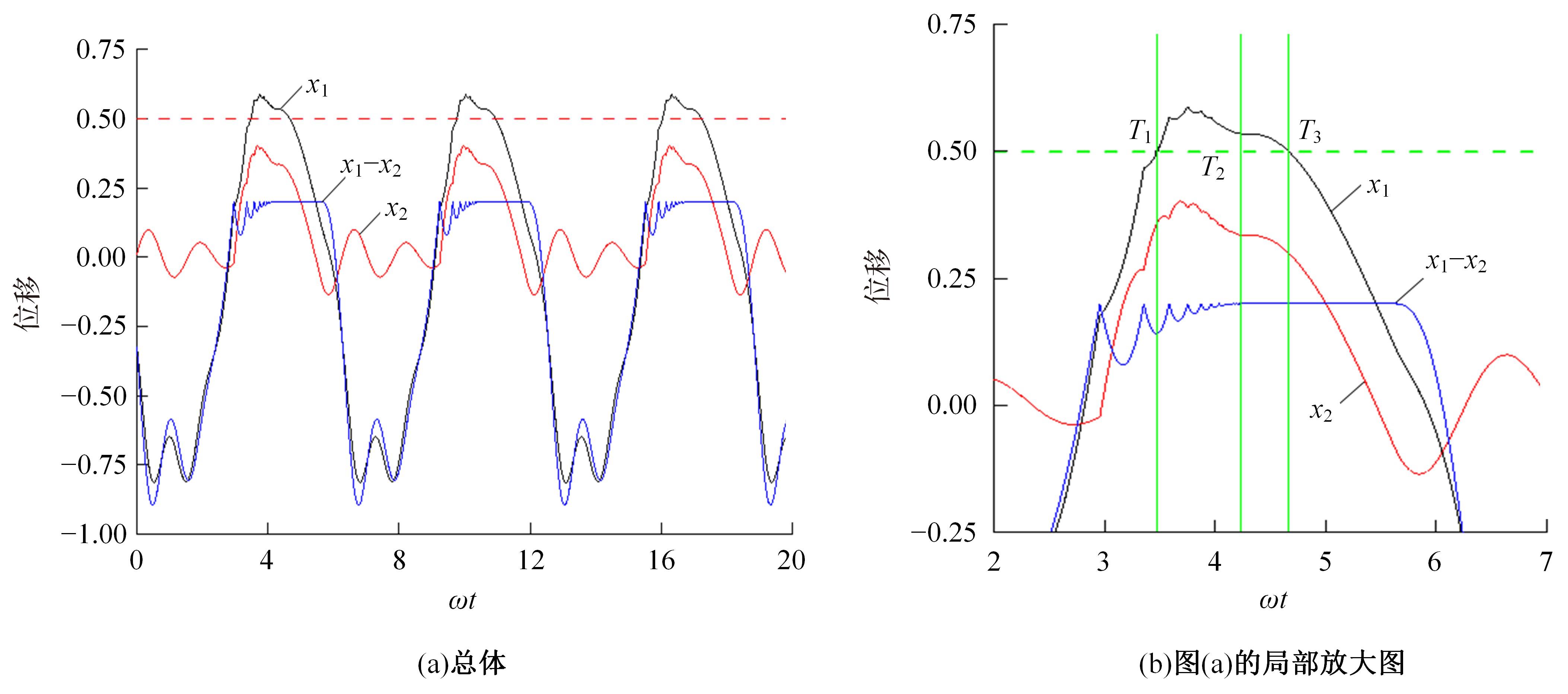
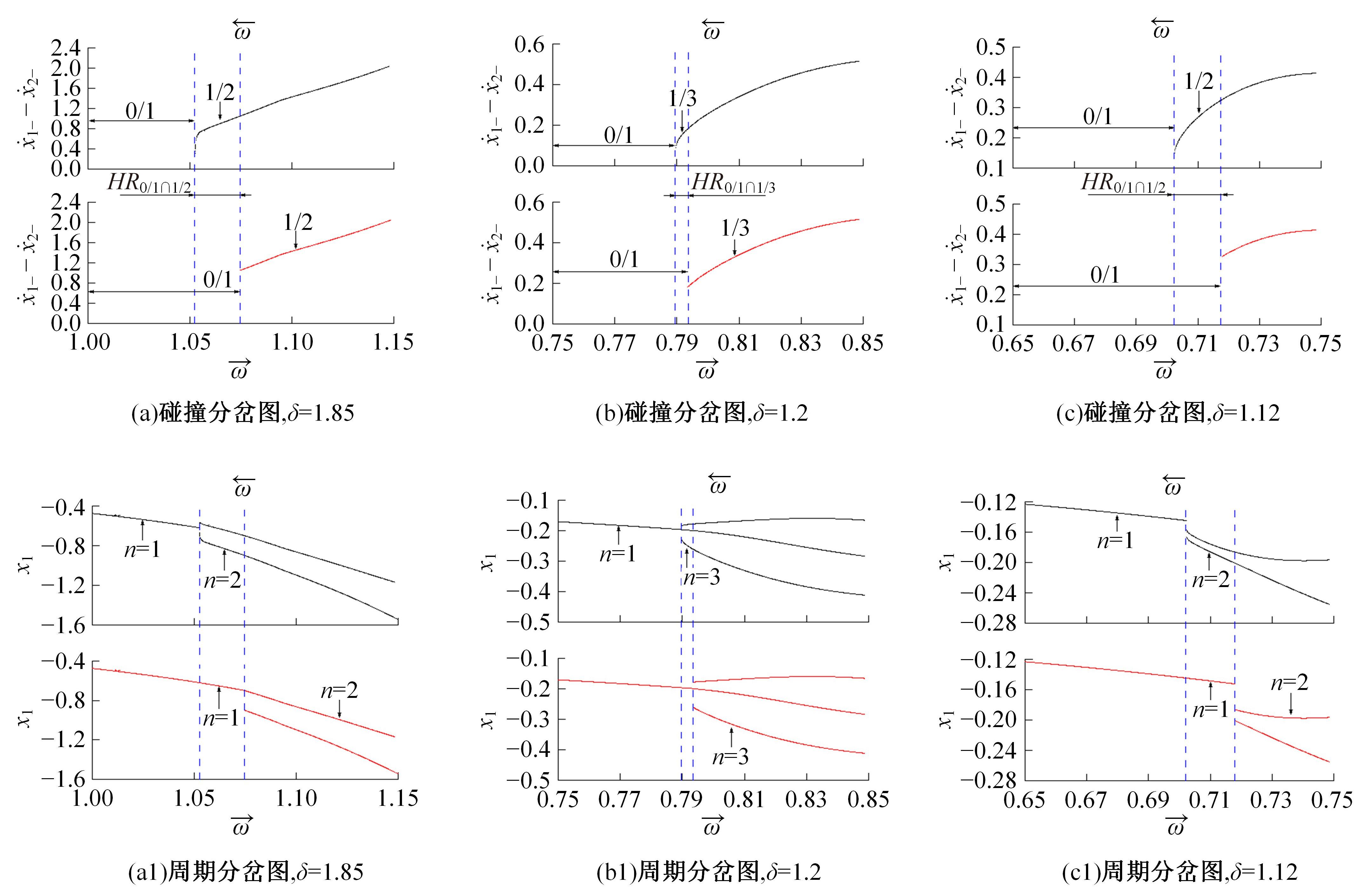
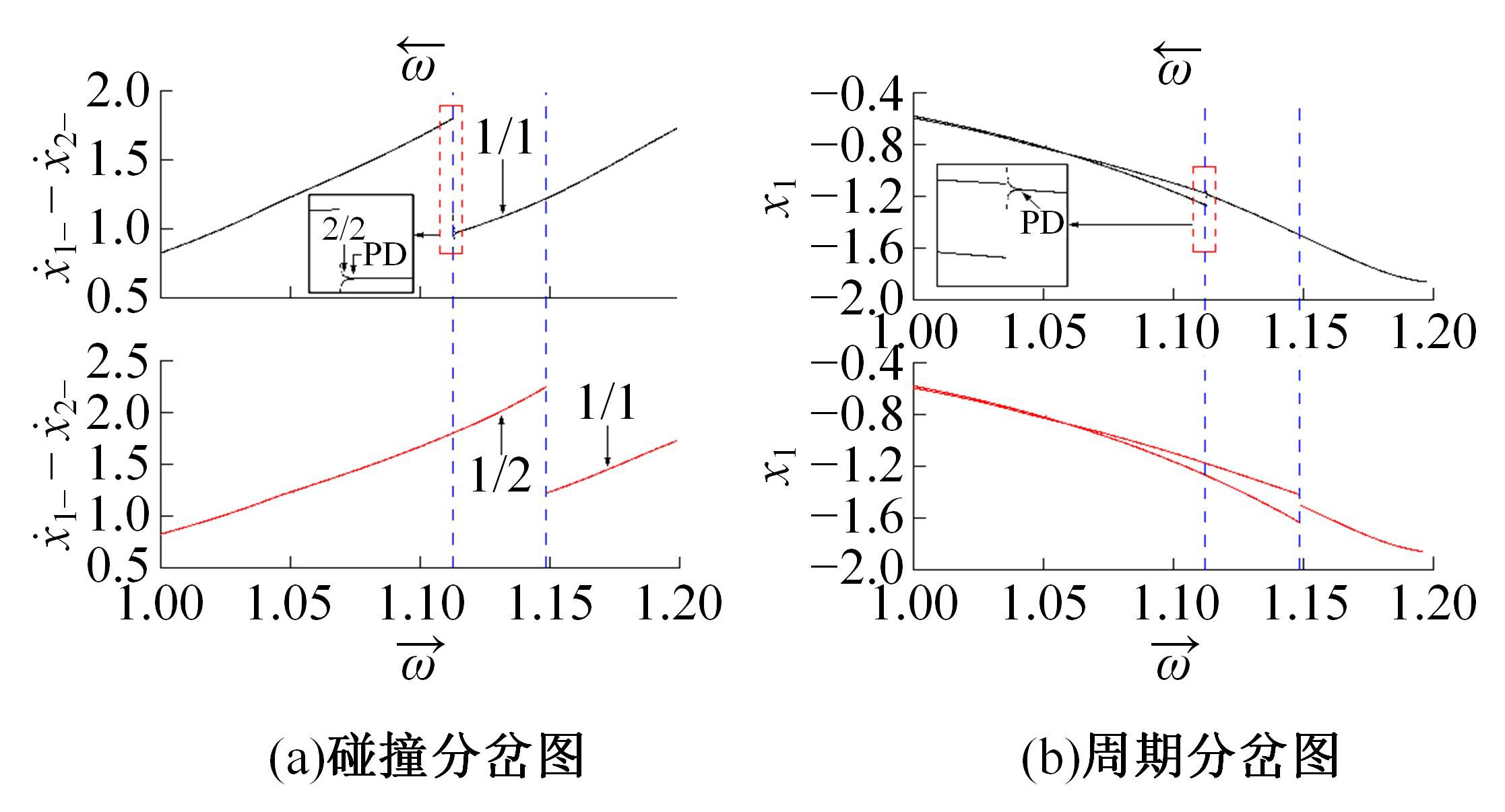
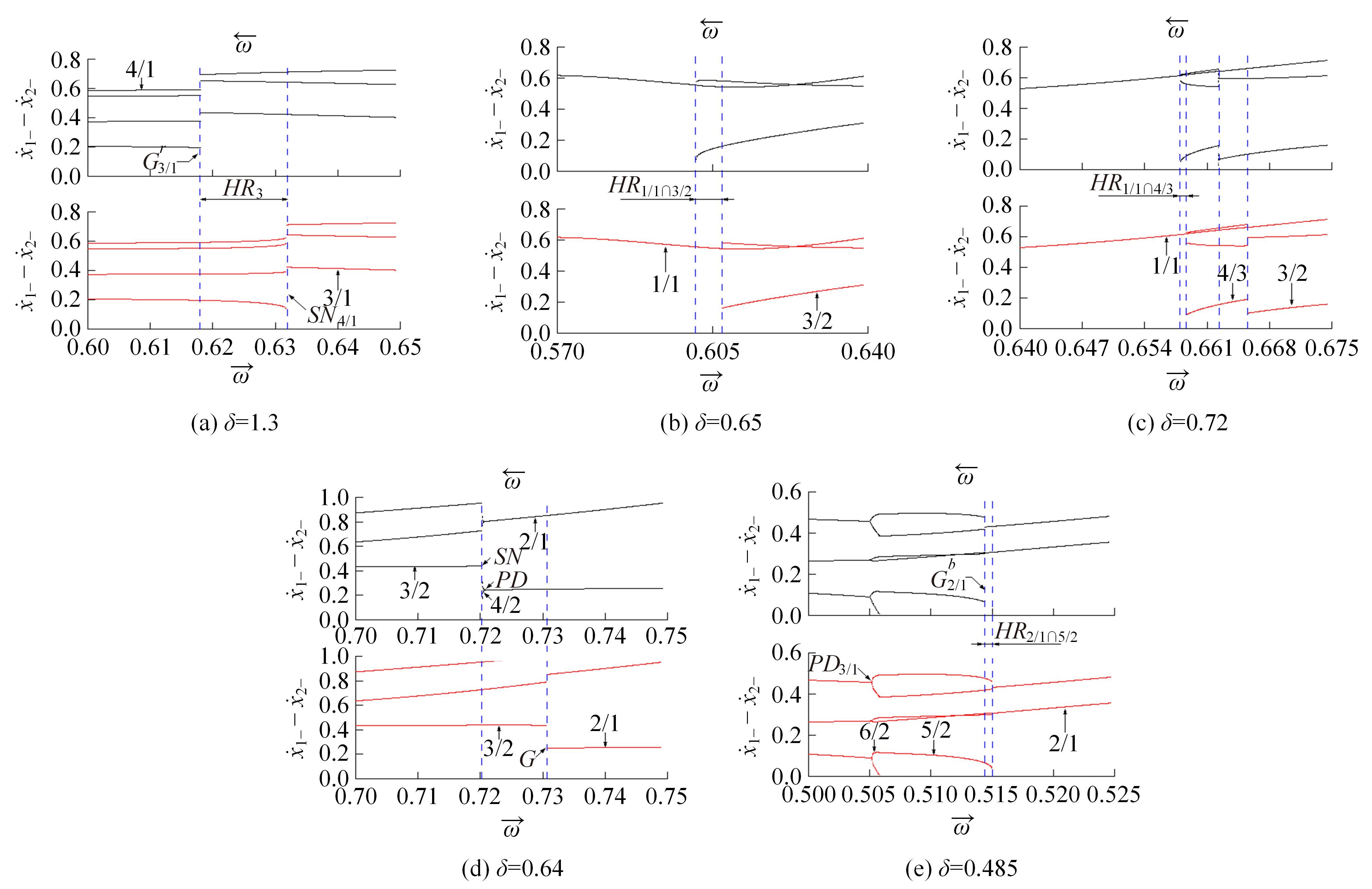
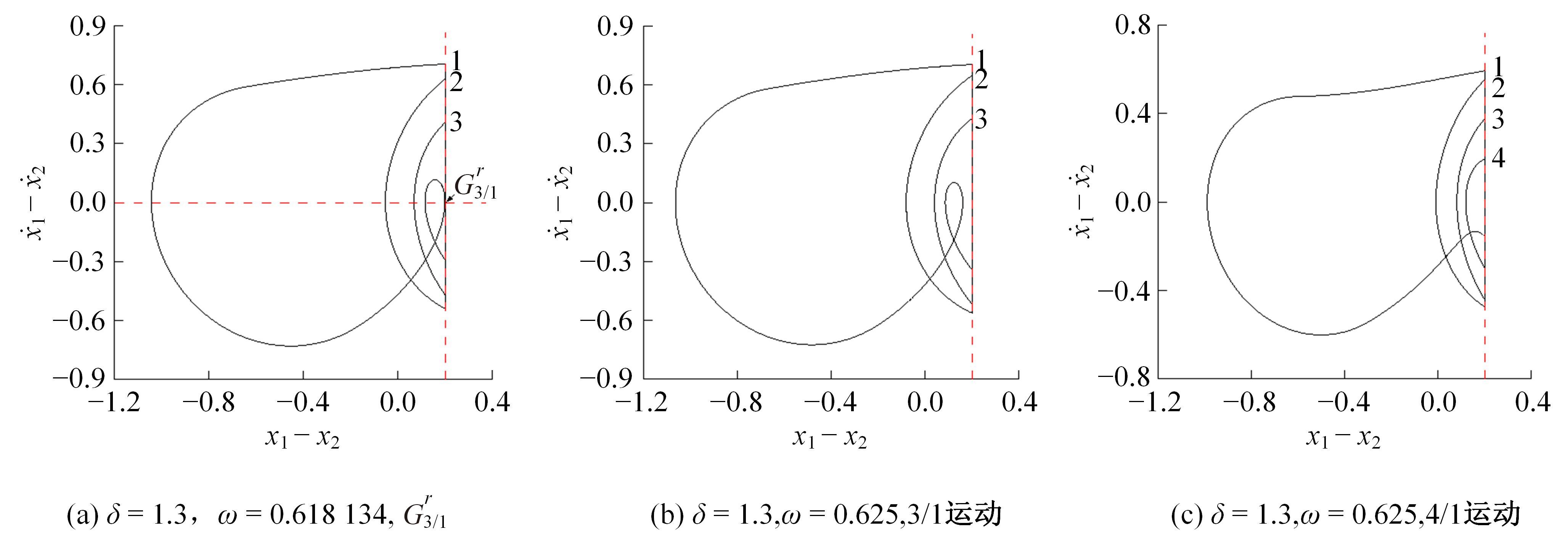
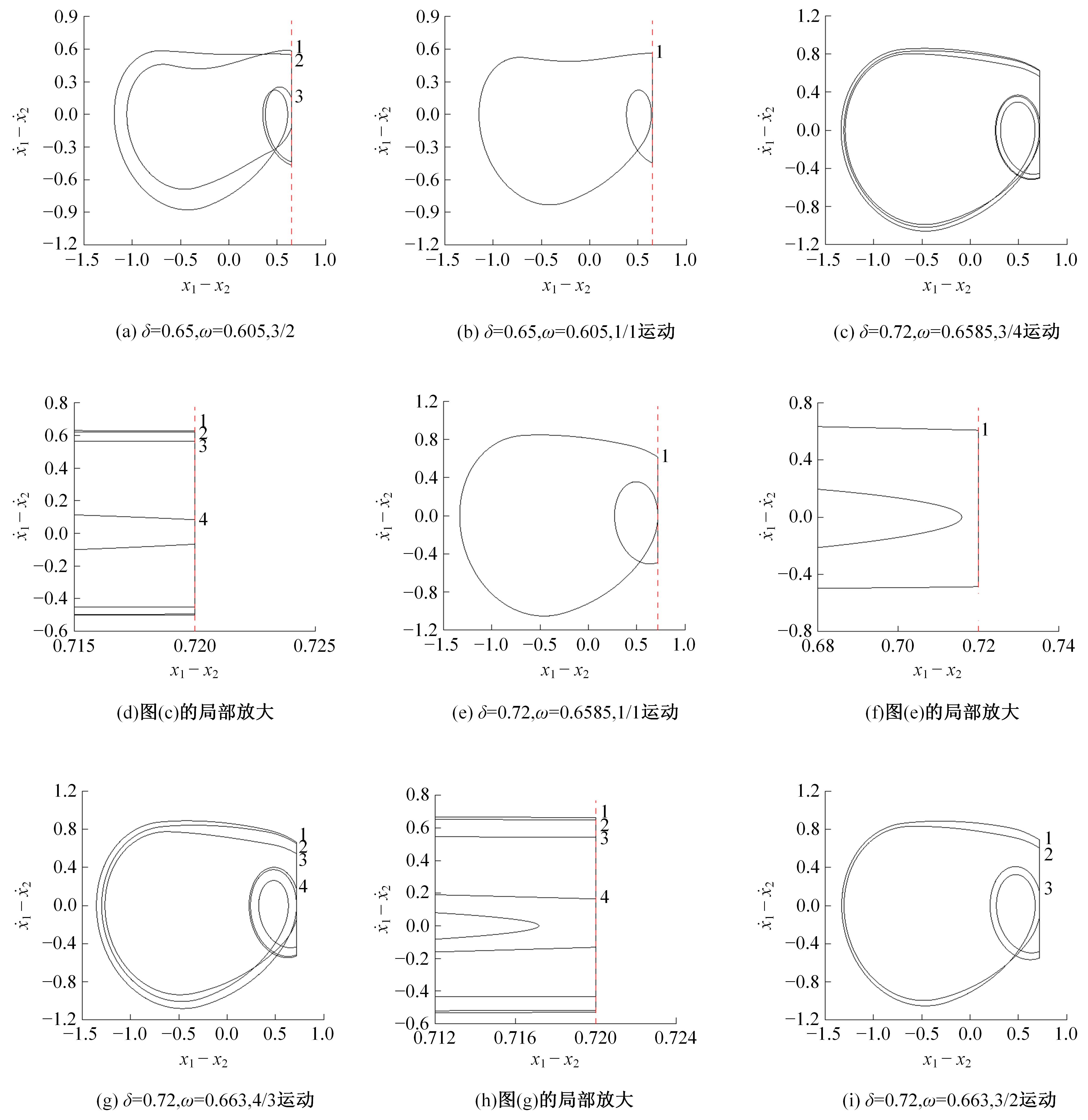
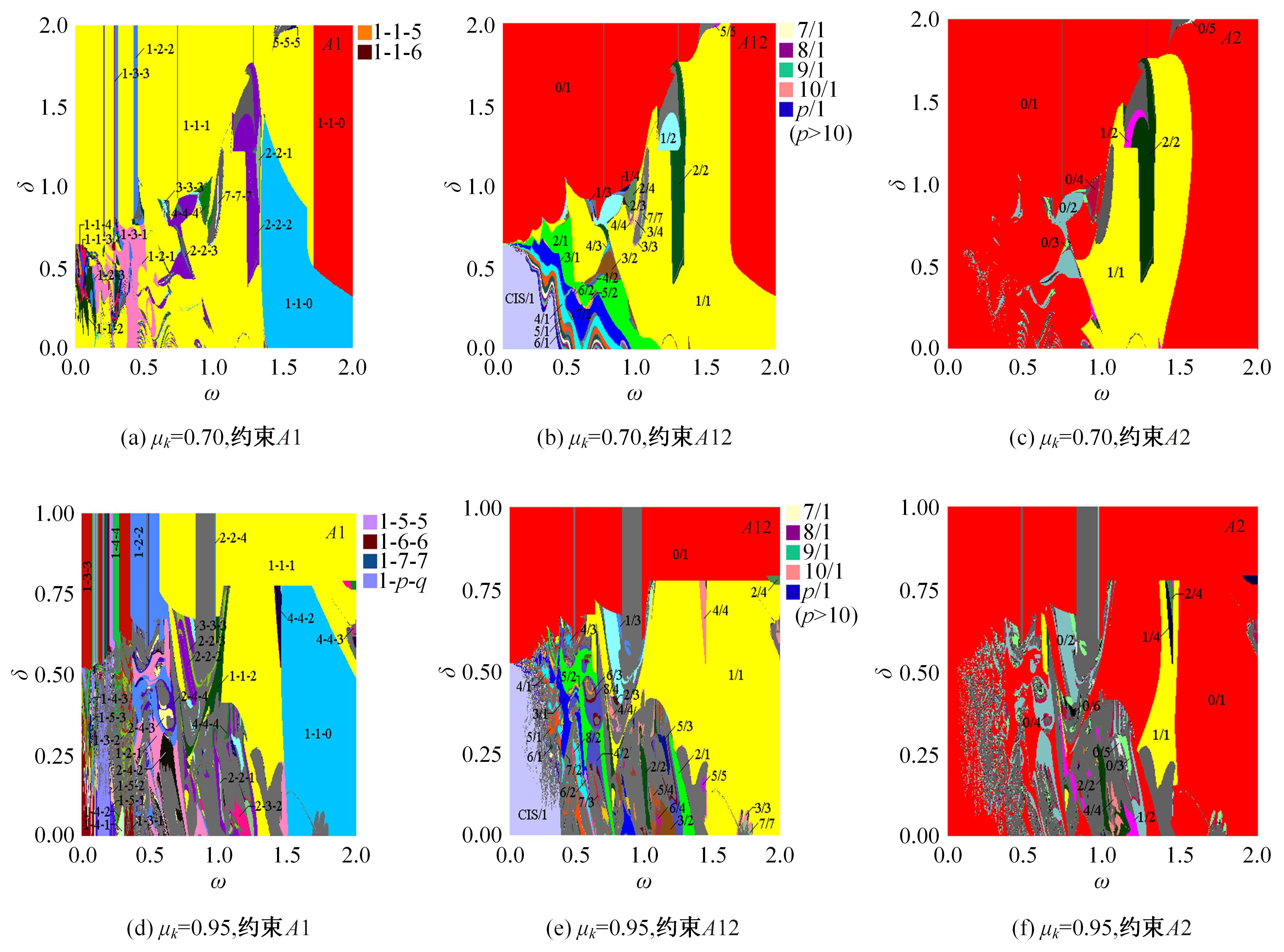
Periodic motion transition characteristics of a vibro-impact system with multiple impact constraints

Shi-jun WANG1,2(),Guan-wei LUO2   

  1. 1.School of Mechatronic Engineering，Lanzhou Jiaotong University，Lanzhou 730070，China
    2.Key Laboratory of System Dynamics and Reliability of Rail Transport Equipment of Gansu Province，Lanzhou 730070，China
  • Received:2022-12-29 Online:2024-04-01 Published:2024-05-17

RICH HTML

 0   

PDF (PC)

97

Abstract:

A type of two-degree-of-freedom forced vibro-impact system with rigid and elastic compound constraints was studied. Based on the numerical calculation method of two-parameter co-simulation， the mode types and existence regions of the periodic motions of the system were obtained on the parameter plane composed of the key parameters excitation force frequency and the gap value between two masses. The transition laws between impactless motion and adjacent fundamental period motion and between adjacent fundamental period motions were revealed. The effect of the change of the elastic constraint stiffness on the types of mode and the region of existence of the periodic motions of the system was analyzed. The results show that there are two main types of transition regions， including tongue-like regions and hysteresis regions， between impactless motion and adjacent fundamental period motion and between adjacent fundamental periodic motions. There are regular subharmonic motions in the tongue-like regions. These subharmonic motions and the adjacent fundamental period motions form a hysteresis region group near the boundary lines of the tongue-like regions. Increasing the stiffness value at the elastic constraint will significantly increase the existence regions of quasi-periodic motions and chaotic motions in the low frequency domain in the two-parameter plane， and divide the existence regions of periodic motions.

Key words: mechanical design, compound constraints, vibro-impact, co-simulation, hysteresis region group, bifurcation

CLC Number: 

  • O322

Fig.1

Mechanical model of a two-degree-of-freedomforced vibration system"

Fig.2

Schematic diagram of two-parameterco-simulation"

Fig.3

Pattern types and distribution regions of periodic motions of the system in the （ω，δ）-parameter plane associated with each constraint"

Fig.4

Global one-parameter bifurcation diagrams of the system at δ = 0.2"

Fig.5

Phase plane portraits of system periodic motion，δ=0.2，ω=1.2"

Fig.6

Time response diagram of displacement，δ=0.2，ω=0.25"

Fig.7

One-parameter bifurcation diagrams， δ = 1.0"

Fig.8

Phase plane portraits，δ=1.0，ω=1.7"

Fig.9

Partial description of Fig.4（b）"

Fig.10

One-parameter bifurcation diagrams for transversely traversing hysteretic region groups"

Fig.11

One-parameter bifurcation diagrams，δ=1.3"

Fig.12

Phase plane portraits"

Fig.13

Pattern types and distribution regions of periodic motions of system in （ω，δ）-parameter plane associated with constraint A12"

Fig.14

One-parameter bifurcation diagrams for transversely traversing hysteretic regions"

Fig.15

Phase plane portraits"

Fig.16

Phase plane portraits"

Fig.17

Pattern types and distribution regions of periodic motions of the system in （ω，δ）-parameter plane withdifferent constraint stiffness ratios μk0"

1 Shaw S W, Holmes P J. A periodically forced piecewise linear oscillator[J]. Journal of Sound and Vibration, 1983, 90(1): 129-155.
2 Nordmark A B. Non-periodic motion caused by grazing incidence in an impact oscillator[J]. Journal of Sound and Vibration, 1991, 145(2): 279-297.
3 Whiston G S. Singularities in vibro-impact dynamics [J]. Journal of Sound and Vibration, 1992, 152(3): 427-460.
4 Hu H Y. Detection of grazing orbits and incident bifurcations of a forced continuous, piecewise-linear oscillator[J]. Journal of Sound and Vibration, 1994, 187(3): 485-493.
5 Foale S, Bishop S R. Bifurcations in impact oscillations[J]. Nonlinear Dynamics, 1994, 6: 285-99.
6 Phanikrishna T, Harry D. Continuous and discontinuous grazing bifurcations in impacting oscillators[J]. Physica D: Nonlinear Phenomena, 2006, 214(2): 187-197.
7 Levitas J, Weller T, Singer J. Poincaré-like simple cell mapping for non-linear dynamical systems[J]. Journal of Sound and Vibration, 1994, 176(5): 641-662.
8 Levitas J, Weller T. Poincare linear interpolated cell mapping: method for global analysis of oscillating systems[J]. Journal of Applied Mechanics, 1995, 62(2): 489-495.
9 石建飞,张艳龙,王丽,等. Duffing系统的双参数分岔与全局特性分析[J]. 噪声与振动控制,2016(6): 32-37.
Shi Jian-fei, Zhang Yan-long, Wang Li, et al. Double-parameter bifurcation and global characteristic analysis of Duffing systems[J]. Noise and Vibration Control, 2016(6):32-37.
10 Shi J F, Zhang Y L, Gou X F. Bifurcation and evolution of a forced and damped Duffing system in two-parameter plane[J]. Nonlinear Dynamics, 2018, 93(2):749-766.
11 Ing J, Pavlovskaia E, Wiercigroch M, et al. Bifurcation analysis of an impact oscillator with a one-sided elastic constraint near grazing[J]. Physica D: Nonlinear Phenomena, 2010, 239(6): 312-321.
12 Liao M L, Ing J, Chávez J P, et al. Bifurcation techniques for stiffness identification of an impact oscillator[J]. Communications in Nonlinear Science and Numerical Simulation, 2016, 41:19-31.
13 Jiang H B, Antonio S E C, Yoshisuke U, et al. Grazing-induced bifurcations in impact oscillators with elastic and rigid constraints[J]. International Journal of Mechanical Sciences, 2017,127:204-214.
14 Liu P F, Zhu L Y, Gou X F, et al. Neighboring periodic motion in spur gear pair and its identification methods[J]. Nonlinear Dynamics, 2021, 106: 2991-3023.
15 苟向锋,朱凌云,陈代林,等.参数耦合对单自由度直齿圆柱齿轮系统动态特性影响分析[J]. 振动工程学报,2017, 30(2): 202-213.
Gou Xiang-feng, Zhu Ling-yun, Chen Dai-lin, et al. Analysis of effect of parameters coupling on the dynamic characteristics of a single degree-of-freedom spur gear system[J]. Journal of Vibration Engineering, 2017,30(2): 202-213.
16 Gou X F, Zhu L Y, Chen D L. Bifurcation and chaos analysis of spur gear pair in two-parameter plane[J]. Nonlinear Dynamics, 2015, 79(3): 2225-2235.
17 Zhang Y X, Xie X P, Luo G W. Multiple nested basin boundaries in nonlinear driven oscillators[J]. Communications in Nonlinear Science and Numerical Simulation, 2017, 44: 220-228.
18 Saunders B E, Vasconcellos R, Kuether R J, et al. Characterization and interaction of geometric and contact/impact nonlinearities in dynamical systems[J]. Mechanical Systems and Signal Processing, 2022, 167(A):No.108481.
19 Czolczynski K, Blazejczyk-Okolewska B, Okolewski A. Analytical and numerical investigations of stable periodic solutions of the impacting oscillator with a moving base[J]. International Journal of Mechanical Sciences, 2016, 115/116: 325-338.
20 Li G F, Wu S P, Wang H B, et al. Global behavior of a simplified model for the micro-vibration molding machine in parameter-state space[J]. Mechanism and Machine Theory, 2020, 154:No.104039.
21 Luo G W, Lyu X H, Zhu X F, et al. Diversity and transition characteristics of sticking and non-sticking periodic impact motions of periodically forced impact systems with large dissipation[J]. Nonlinear Dynamics, 2018, 94: 1047-1079.
22 石建飞,苟向锋,张艳龙.两自由度减振镗杆系统的安全盆侵蚀与分岔‍[J].振动与冲击,2018,37(22): 238-244.
Shi Jian-fei, Gou Xiang-feng, Zhang Yan-long. Erosion and bifurcation of the safe basin of a two-degree- of-freedom damping boring bar system‍[J]. Journal of Vibration and Shock, 2018, 37(22): 238-244.
[1] Wei SUN,Jun YANG. Finite element modeling and vibration reduction analysis of cylindrical shell structures with equal⁃angle attachment of piezoelectric shunt patches [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(2): 365-374.
[2] Bin HU,Yi-quan CAI,Xin LUO,Zi-bin MAO,Jun-wei LI,Meng-yu GUO,Jian WANG. Theory and experiment of high⁃speed seed filling in limited gear⁃shaped side space based on seeds group stress [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(2): 574-588.
[3] Jia-yi WANG,Xin-hui LIU,Zhan WANG,Jin-shi CHEN,Ya-fang HAN,Yu-qi WANG. Flow characteristics analysis of constant flow control valve based on AMESim [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(9): 2499-2507.
[4] Ya-bing CHENG,Ze-yu YANG,Yan LI,Li-chi AN,Ze-hui XU,Peng-yu CAO,Lu-xiang CHEN. Vibration and noise characteristics base on timing silent chain system of hybrid electric vehicle [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(9): 2465-2473.
[5] Yan YANG,Yu-qing SHI,Xiao-rong ZHANG,Guan-wei LUO. Dynamic stability analysis of a amplitude⁃limited vibration system with multiple rigid constraints [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(2): 364-375.
[6] Jian-feng SONG,Xin-lei HUANG,Shuai YI,Zhen-xi YANG,Yong-gang DONG,Shu-lin LI. Temperature field and stress-strain distribution of tread during train braking [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(10): 2773-2784.
[7] Yang LIU. Calculation method of anti-backward-tilting buffer force of luffing jib tower crane [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(10): 2785-2794.
[8] Yang LIU. Unloading impact simulation and test of luffing jib tower crane [J]. Journal of Jilin University(Engineering and Technology Edition), 2022, 52(6): 1292-1300.
[9] Ya-bing CHENG,Lu-xiang CHEN,Ping-yu GE,Ze-yu YANG,Peng-yu CAO. Dynamic simulation analysis and wear failure of dual-phase timing bush chain [J]. Journal of Jilin University(Engineering and Technology Edition), 2022, 52(4): 781-788.
[10] Yang ZHAO,Yang XIAO,Hao SUN,Wen-hao HUO,Song FENG,Yong LIAO. Numerical simulation of micro pitting damage characteristics of lubricated contact gears based on contour integral [J]. Journal of Jilin University(Engineering and Technology Edition), 2022, 52(4): 799-810.
[11] Tong-jian WANG,Shu-wei YANG,Xiao-dan TAN,Jin-shi CHEN,Tong-wen LIU,Zhen-ling ZHI. Performance analysis of hydraulic excavator based on DEM-MBD co-simulation [J]. Journal of Jilin University(Engineering and Technology Edition), 2022, 52(4): 811-818.
[12] Long ZHANG,Tian-peng XU,Chao-bing WANG,Jian-yu YI,Can-zhuang ZHEN. Gearbox fault diagnosis baed on convolutional gated recurrent network [J]. Journal of Jilin University(Engineering and Technology Edition), 2022, 52(2): 368-376.
[13] Wei ZHENG,Jian-jun SUN,Chen-bo MA,Qiu-ping YU,Yu-yan ZHANG,Tao NIU. Research status and prospect of automobile wheel hub machining fixture [J]. Journal of Jilin University(Engineering and Technology Edition), 2022, 52(1): 25-36.
[14] Xiao-chao TIAN,Hai-gang WANG,Hu WANG,Zhi-cong WANG,Jian ZHAO,Zhi-gang YANG,Yue WU. Design and test of broadband power generation device with cantilever piezoelectric vibrator [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(6): 1953-1958.
[15] Wei CHEN,Yu-long LEI,Xing-zhong LI,Yao FU,Jian-long HU,Li-guo HOU. Calculation of adhesive wear of involute cylindrical spur gear under low⁃speed conditions [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(5): 1628-1634.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
Copyright © Journal of Jilin University(Engineering and Technology Edition), All Rights Reserved.
Tel: +86-431-85095297　Fax: +86-431-85094074　E-mail: xbgxb@jlu.edu.cn
Powered by Beijing Magtech Co. Ltd