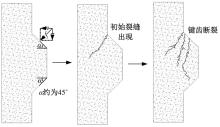
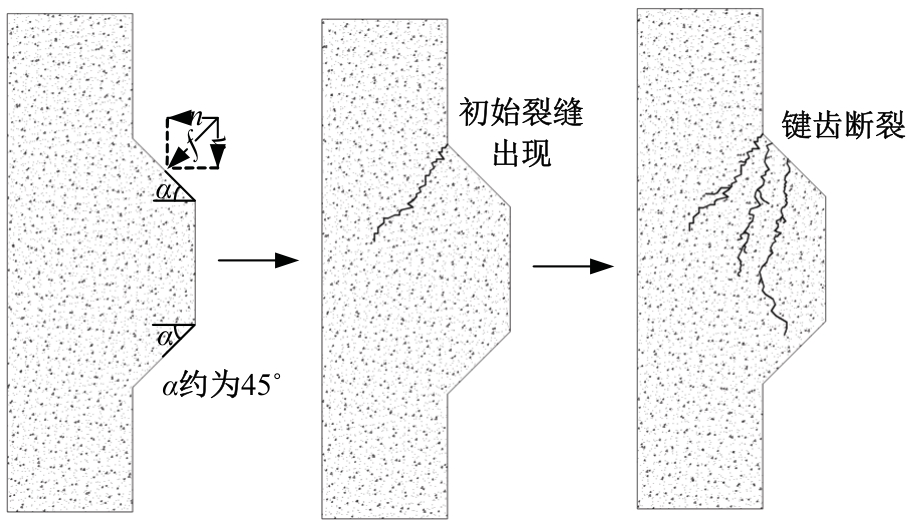
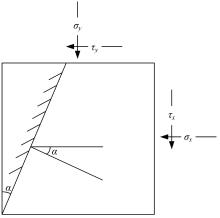
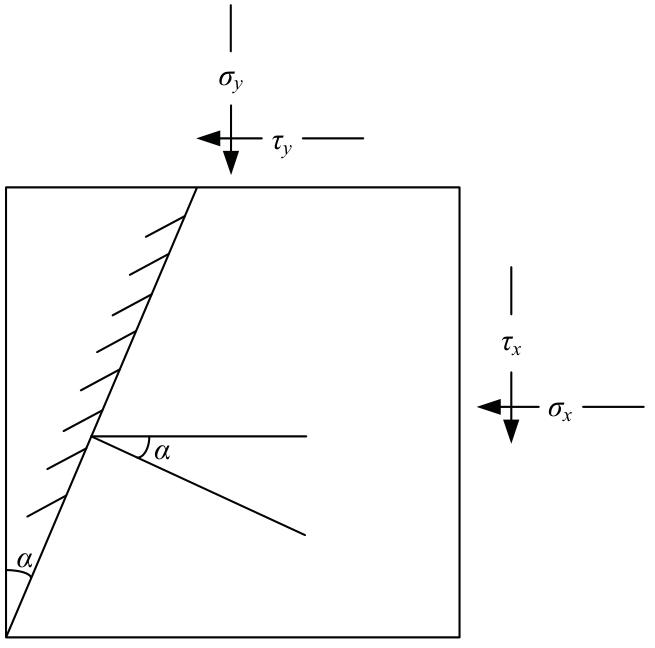
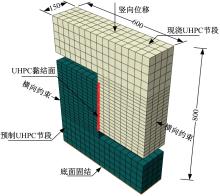
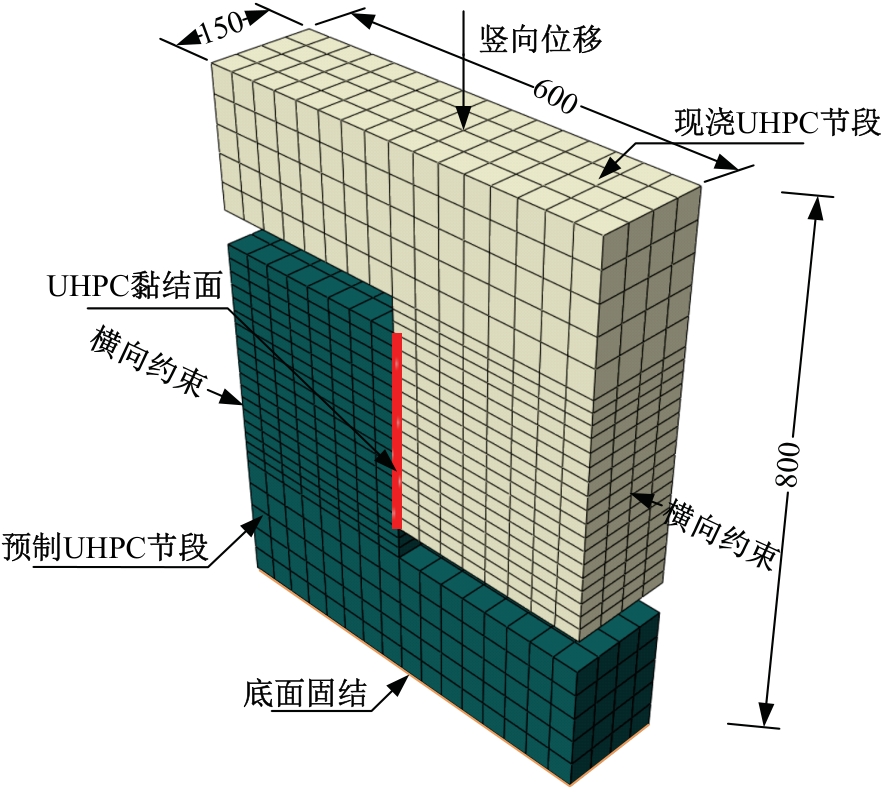
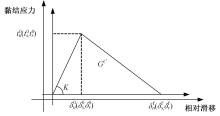
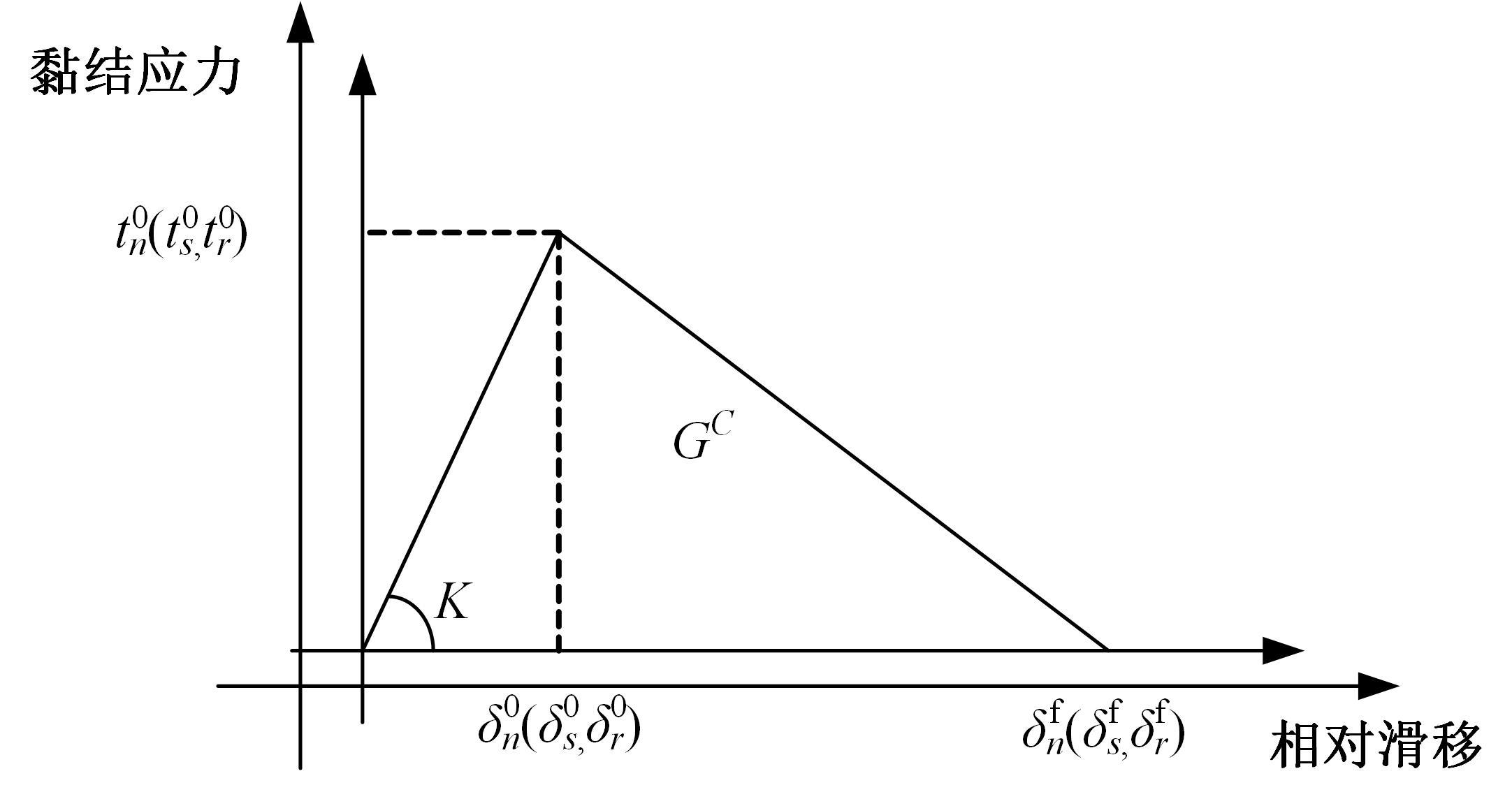
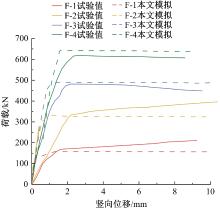
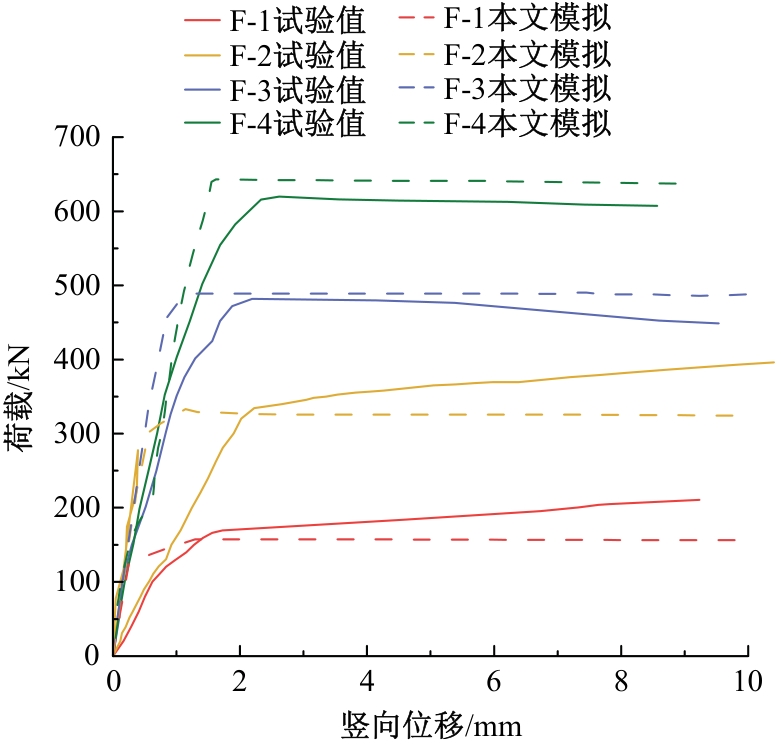
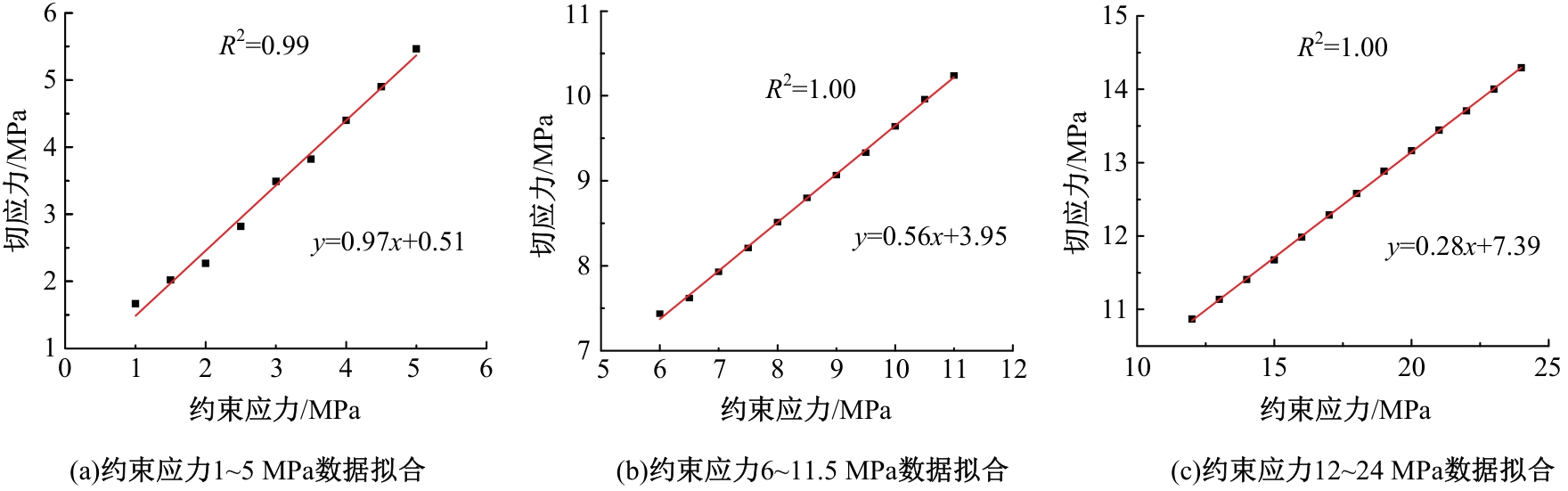
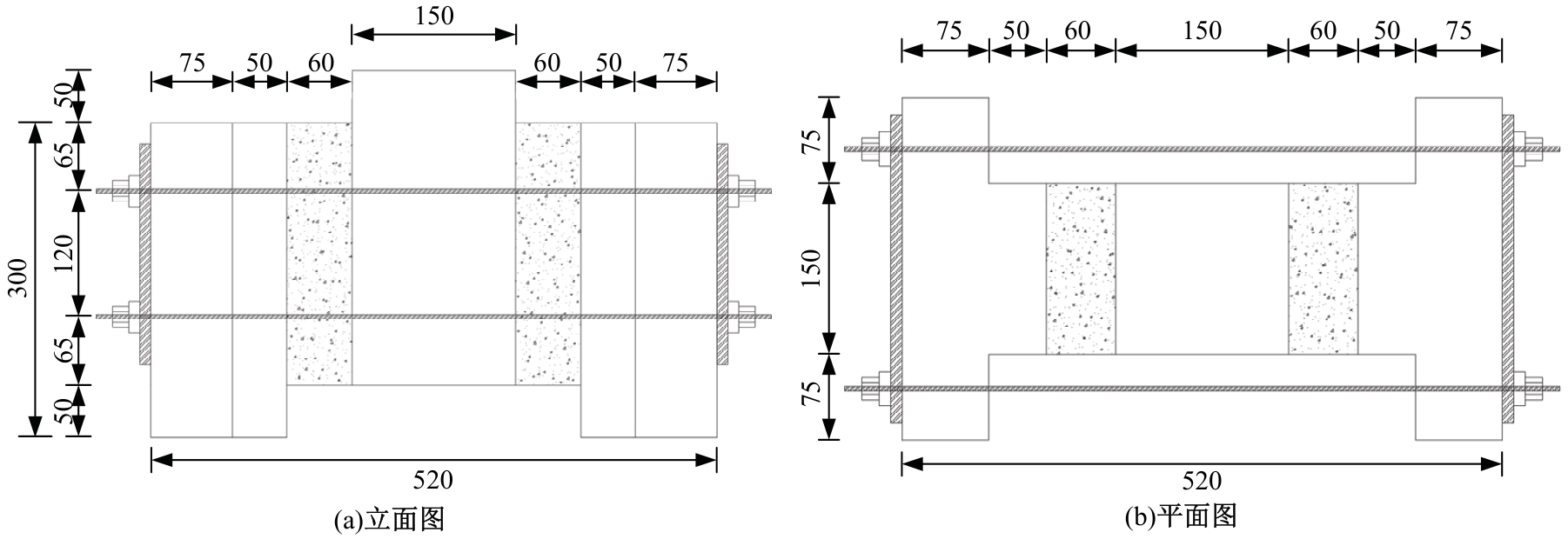
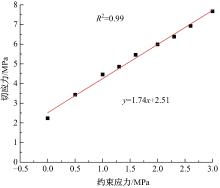
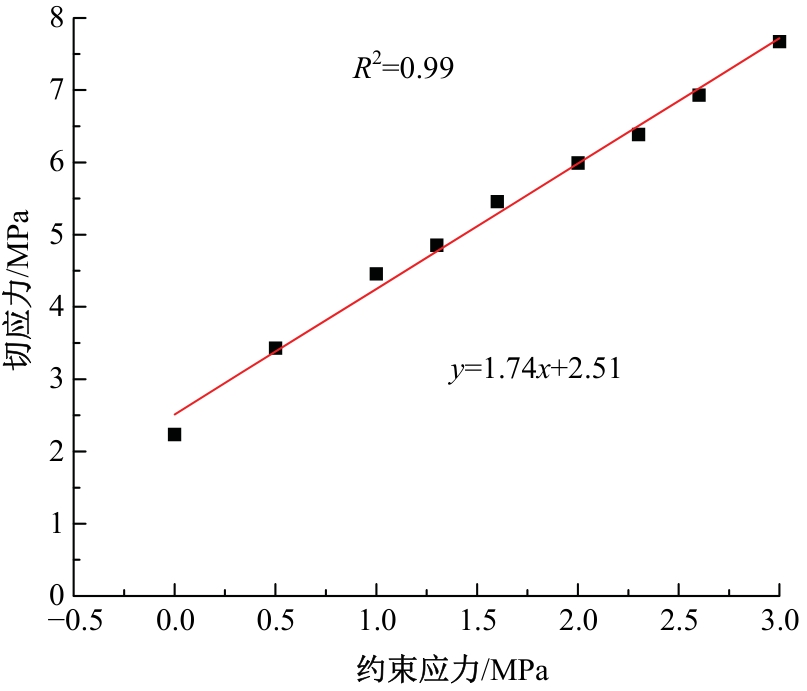
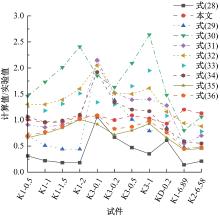
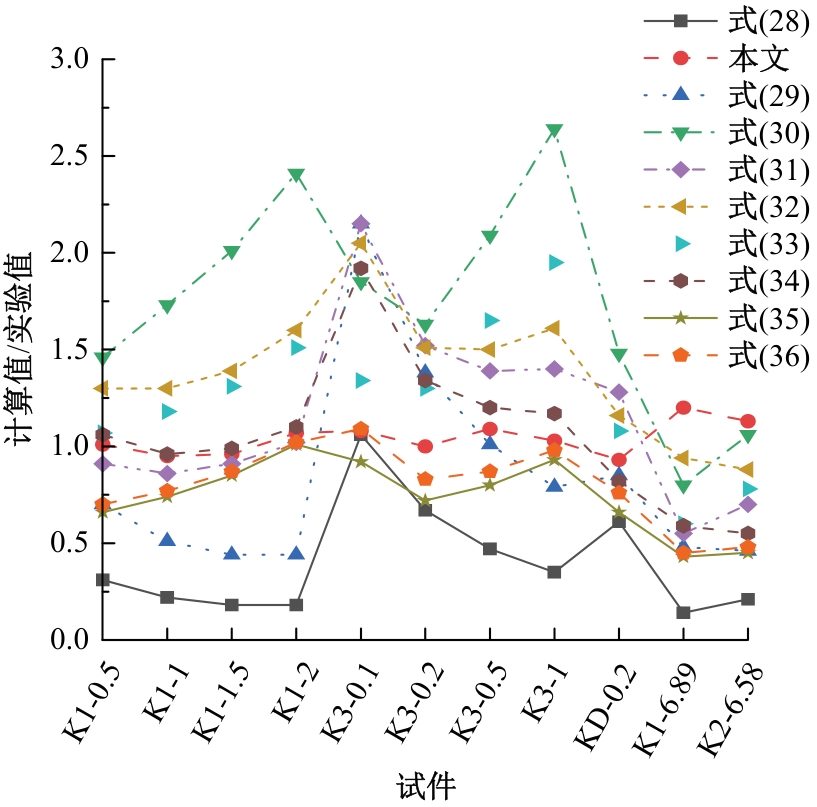
Journal of Jilin University(Engineering and Technology Edition) ›› 2025, Vol. 55 ›› Issue (12): 3928-3941.doi: 10.13229/j.cnki.jdxbgxb.20240450
Direct shear strength of UHPC wet joints in precast piers
Mi ZHOU1( ),Xing-wang TIAN1,Guo-qiang ZHU1,Lei MA2
),Xing-wang TIAN1,Guo-qiang ZHU1,Lei MA2
- 1.Key Laboratory for Old Bridge Detection and Reinforcement Technology of the Ministry of Transportation,Chang'an University,Xi'an 710064,China
2.CCCC Second Highway Engineering Co. ,Ltd. ,Xi'an 710064,China
CLC Number:
- U443
| [1] | Jones L L. Shear test on joints between precast post-tensioned units[J]. Magazine of Concrete Research, 1959, 11(31): 25-30. |
| [2] | Koseki K, Breen J E. Exploratory study of shear strength of joints for precast segmental bridges[R]. Center for Transportation Research, the University of Texas at Austin, 1983: 33-52. |
| [3] | ACI 318-83. Buliding code requirement for reinforce concrete [S]. |
| [4] | Buyukozturk O, Bakhoum M M, Michael B S. Shear behavior of joints in precast concrete segmental bridges[J]. Journal of Structural Engineering, 1990, 116(12): 3380-3401. |
| [5] | Rombach G A. Precast segmental box girder bridges with external prestressing: design and construction[J]. Segmental Bridges, 2002, 19(2): 1-15. |
| [6] | 卢文良. 节段预制体外预应力混凝土梁设计理论研究[D]. 北京: 北京交通大学土木建筑工程学院, 2004. |
| Lu Wen-liang. Study on the design theory of segmental precast concrete girders with external tendons[D]. Beijing: School of Civil Engineering, Beijing Jiaotong University,2004. | |
| [7] | AASHTO. LRFD bridge design specifications [S/OL]. [2024-01-15]. |
| [8] | 王建超. 节段预制拼装混凝土桥梁接缝抗剪性能试验研究[D]. 南京: 东南大学土木工程学院, 2011. |
| Wang Jian-chao. ExperimentaI study on shear behaviour of joints in precast concnte segmental bridges[D]Nanjing: School of Civil Engineering, Southeast University, 2011. | |
| [9] | 邹琳斌. 体外预应力节段施工混凝土桥梁湿接缝剪切性能研究[D]. 广州: 广东工业大学土木与交通工程学院, 2012. |
| Zou Lin-bin. Research on shear properties of dry joints insegmental precast concrete bridge with external tendons[D]. Guangzhou:School of Civil and Transport Engineering, Guangdong University of Technology, 2012. | |
| [10] | 陈黎. 预制节段式混凝土桥梁干接缝抗剪性能研究 [D]. 广州: 广东工业大学 土木与交通工程学院,2013. |
| Chen Li. Research on shear behavior of dry joints in precast segmental concrete bridge[D]. Guangzhou:School of Civil and Transport Engineering, Guangdong University of Technology,2013. | |
| [11] | 姜海波, 李宇鸿, 肖杰, 等. 预制节段干接缝体外预应力混凝土简支梁抗剪性能试验 [J]. 中国公路学报, 2018, 31(12): 188-195. |
| Jiang Hai-bo, Li Yu-hong, Xiao Jie, et al. Shear behavior of precast concrete segmental simply supported beam with external tendons and dry joints [J]. China Journal of Highway and Transport, 2018, 31(12): 188-195. | |
| [12] | Wakasa T, Otsuka H, Yabuki W. Expermental study of the shear strength of precast segmental beams with external prestressing[J]. Structure Concrete, 2005(6): 63-80. |
| [13] | 闫泽宇.节段预制拼装UHPC接缝抗剪性能研究[D].长沙: 湖南大学土木工程学院,2019. |
| Yan Ze-yu. Study on shear performance of joints in precast UHPC segmental bridge[D].Changsha:College of Civil Engineering, Hunan University,2019. | |
| [14] | Jiang H B, Shao T F, Fang Z C, et al. Shear-friction behavior of grooved construction joints between a precast UHPC girder and a cast-in-place concrete slab[J]. Engineering Structures, 2021, 228: No.111610. |
| [15] | 刘桐旭. 节段预制拼装UHPC梁接缝抗剪性能试验与理论研究[D]. 南京: 东南大学土木工程学院,2017. |
| Liu Tong-xu. Experimental and theoretical research on shear behavior of joints in precast UHPC segmental bridges[D].Nanjing:School of Civil Engineering, Southeast University,2017. | |
| [16] | 王振领. 新老混凝土粘结理论与试验及在桥梁加固工程中的应用研究 [D]. 成都: 西南交通大学土木工程学院, 2006. |
| Wang Zhen-ling. Study on bond theory and test of new and old concrete and its application in bridge strengthening engineering[D].Chengdu:School of Civil Engineering, Southwest Jiaotong University,2006. | |
| [17] | Aaleti S, Petersen B, Sritharan S. Design guide for p recast uhpc waffle deck panel system, including connections[R]. Washington D C:Federal Highway Administration, 2013. |
| [18] | Graybeal B. Ultra-high-performance concrete connections for precast concrete bridge decks[J]. PCI Journal, 2014, 59 (4): 48-62. |
| [19] | 邵旭东, 管亚萍, 晏班夫. 预制超高性能混凝土π形梁桥的设计与初步试验[J]. 中国公路学报, 2018, 31(1): 46-56. |
| Shao Xu-dong, Guan Ya-ping, Yan Ban-fu. Design and preliminary experiments of UHPC π-shaped girder bridge[J]. China Journal of Highway and Transport, 2018, 31(1): 46-56. | |
| [20] | 张孝臣. 预制超高性能混凝土修复既有混凝土结构界面粘结性能研究 [D]. 哈尔滨: 哈尔滨工业大学土木工程学院, 2016. |
| Zhang Xiao-chen. Study of interface bond behavior between precast ultra high performance concrete repaired and exsiting concrete structure[D]. Harbin:School of Civil Engineering, Harbin Institute of Technology,2016. | |
| [21] | Victor G, Jed L, Michael P, et al. Fracture mechanics testing of the bond between composite overlays and a concrete substrate[J]. Journal of Adhesion Science and Technology, 2001, 15(11): 1351-1371. |
| [22] | 吴威业. 预制节段拼装桥墩抗剪性能研究[D]. 宁波: 宁波大学土木工程与地理环境学院, 2017. |
| Wu Wei-ye. Shear resistant performance investigation of precast segmental bridge columns[D]. Ningbo:School of Civil and Environmental Engineering and Geography Science, Ningbo University,2017. | |
| [23] | 过镇海, 张秀琴. 砼受拉应力-变形全曲线的试验研究[J]. 建筑结构学报, 1988(4): 45-53. |
| Guo Zhen-hai, Zhang Xiu-qin. Experimental investigation of complete stress-deformation curves of concrete intension [J]. Journal of Building Structures, 1988(4): 45-53. | |
| [24] | Qi J, Ma Z J, Wang J. Shear strength of UHPFRC beams: mesoscale fiber-matrix discrete model[J]. Journal of Structural Engineering, 2016, 143:No. 0401629. |
| [25] | Turmo J, Ramos G, Aparicio A C. FEM modelling of unbonded post-tensioned segmental beams with dry joints[J]. Engineering structures, 2006, 28(13): 1852-1863. |
| [26] | 孙雪帅. 预制拼装桥梁节段间接缝抗剪性能试验研究 [D]. 南京: 东南大学土木工程学院,2015. |
| Sun Xue-shuai. Experimental study on shear behavior of joints in precast segmental bridges[D]. Nanjing: School of Civil Engineering, Southeast University,2015. | |
| [27] | 冯峥, 李传习, 周佳乐,等. UHPC键齿湿接缝直剪试验及湿接缝直剪承载力统一公式[J]. 土木工程学报, 2022, 55(6): 79-91. |
| Feng Zheng, Li Chuan-xi, Zhou Jia-le, et al. Direct shear test on UHPC key-wet-joints and the unified calculation formula of direct shear capacity of UHPC wet-joints[J]. China Civil Engineering Journal, 2022, 55(6): 79-91. | |
| [28] | 吴威业. 预制节段拼装桥墩抗剪性能研究[D]. 宁波: 宁波大学土木工程与地理环境学院, 2017. |
| Wu Wei-ye. Shear resistant performance investigation of precast segmental bridge columns[D]. Ningbo:School of Civil&Environmental Engineer and Geography Science,Ningbo University, 2017. | |
| [29] | Shamass R, Zhou X, Alfano G. Finite-element analysis of shear-off failure of shear-off failure of keyed dry joints in precast concrete segmental bridges[J]. Journal of Bridge Engineering, 2014, 20(6):No. 04014084. |
| [30] | 马雷. 预制装配式桥墩UHPC湿接缝抗剪性能研究[D]. 西安: 长安大学公路学院, 2022. |
| Ma Lei. Research on shear performance of UHPC wet joints in assembled segmental column[D]. Xi'an: Highway School, Chang'an University, 2022. | |
| [31] | Hussein H H, Walsh K K, Sargand S M, et al. Modeling the shear connection in adjacent box-beam bridges with ultrahigh-performance concrete joints. I: model calibration and validation[J]. Journal of Bridge Engineering, 2017, 22(8): No. 04017043. |
| [1] | Liang FAN,Wen ZENG,Qiang WEN,Fu-yu ZHAO,Ying-ming XU. Vibration characteristics of prefabricated steel-concrete composite beam bridges with clustered grouping bolt connection and analysis of vehicle-bridge coupling [J]. Journal of Jilin University(Engineering and Technology Edition), 2025, 55(7): 2354-2364. |
| [2] | Yong-jun ZHOU,Feng-rui MU,Cheng CAI,Fan YANG. Influence factors of preload loss in cable clamp bolt of suspension bridge based on orthogonal experiment method [J]. Journal of Jilin University(Engineering and Technology Edition), 2025, 55(4): 1188-1196. |
| [3] | Bao-dong LIU,Fang LI,Xiao-xi WANG,Meng GAO. Flexural stiffness and bearing capacity of corrugated steel plate composite structures reinforced by concrete [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(9): 2502-2510. |
| [4] | Yong-xin SUN,Peng-zhen LIN,Zi-jiang YANG,Wei JI. Calculation method for crack width of UHPC beams considering bond slip effect [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(9): 2600-2608. |
| [5] | Yu-xin XUE,Yong-jun ZHOU,Ye-lu WANG,Kai-xiang FAN,Yu ZHAO. Application of dynamic load allowance test method of simply supported girder bridge based on suspension hammer system [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(9): 2557-2567. |
| [6] | Xue-lian GUO,Wan-shui HAN,Tao WANG,Kai ZHOU,Xiu-shi ZHANG,Shu-ying ZHANG. Assessment method of resistant overturning stability safety factors of curved bridge under customized transport vehicles [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(8): 2229-2237. |
| [7] | Lin XIAO,Huan-bo WEI,Xing WEI,Zhi-rui KANG. Numerical analysis on cracking behavior of concrete slab due to corrosion expansion of stud connector in steel-concrete composite beam [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(7): 1958-1965. |
| [8] | Han-hui HUANG,Kang-ming CHEN,Qing-xiong WU. Flexural behavior of composite continuous girders with concrete-filled steel tubular truss chords [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(6): 1665-1676. |
| [9] | Chun-lei ZHANG,Chang-yu SHAO,Qing-tian SU,Chang-yuan DAI. Experimental on positive bending behaviour of composite bridge decks with steel-fiber-reinforced concrete and longitudinal bulb-flat ribs [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(6): 1634-1642. |
| [10] | Chang-jiang SHAO,Hao-meng CUI,Qi-ming QI,Wei-lin ZHUANG. Longitudinal seismic mitigation of near⁃fault long⁃span RC soft⁃lighten arch bridge based on viscous damper [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(5): 1355-1367. |
| [11] | Qiu ZHAO,Peng CHEN,Yu-wei ZHAO,Ao YU. Overall mechanical performance of jointless bridges with arch structure behind abutment [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(4): 1016-1027. |
| [12] | Hong ZHANG,Zhi-wei ZHU,Tian-yu HU,Yan-feng GONG,Jian-ting ZHOU. Bridge bolt defect identification method based on improved YOLOv5s [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(3): 749-760. |
| [13] | Guo-jun YANG,Ya-hui QI,Xiu-ming SHI. Review of bridge crack detection based on digital image technology [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(2): 313-332. |
| [14] | Zhi-qiang HAN,Gang XIE,Ya-juan ZHUO,Zuo-long LUO,Hua-teng LI. Vibration response of continuous girder bridge based on wheel⁃deck coherent excitation [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(2): 436-444. |
| [15] | Xing WEI,Yong-qi ZHANG,Jun-ming ZHAO,Hui-jun WANG,Lin XIAO. Hot spot stress concentration factor for welded skewed-T joints [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(12): 3478-3485. |
|
||