扭转荷载下螺旋形螺纹连接件的IWAN改进模型

doi:10.13229/j.cnki.jdxbgxb.20210914

摘要/Abstract

摘要：

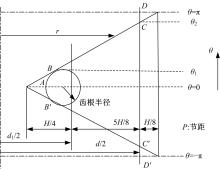
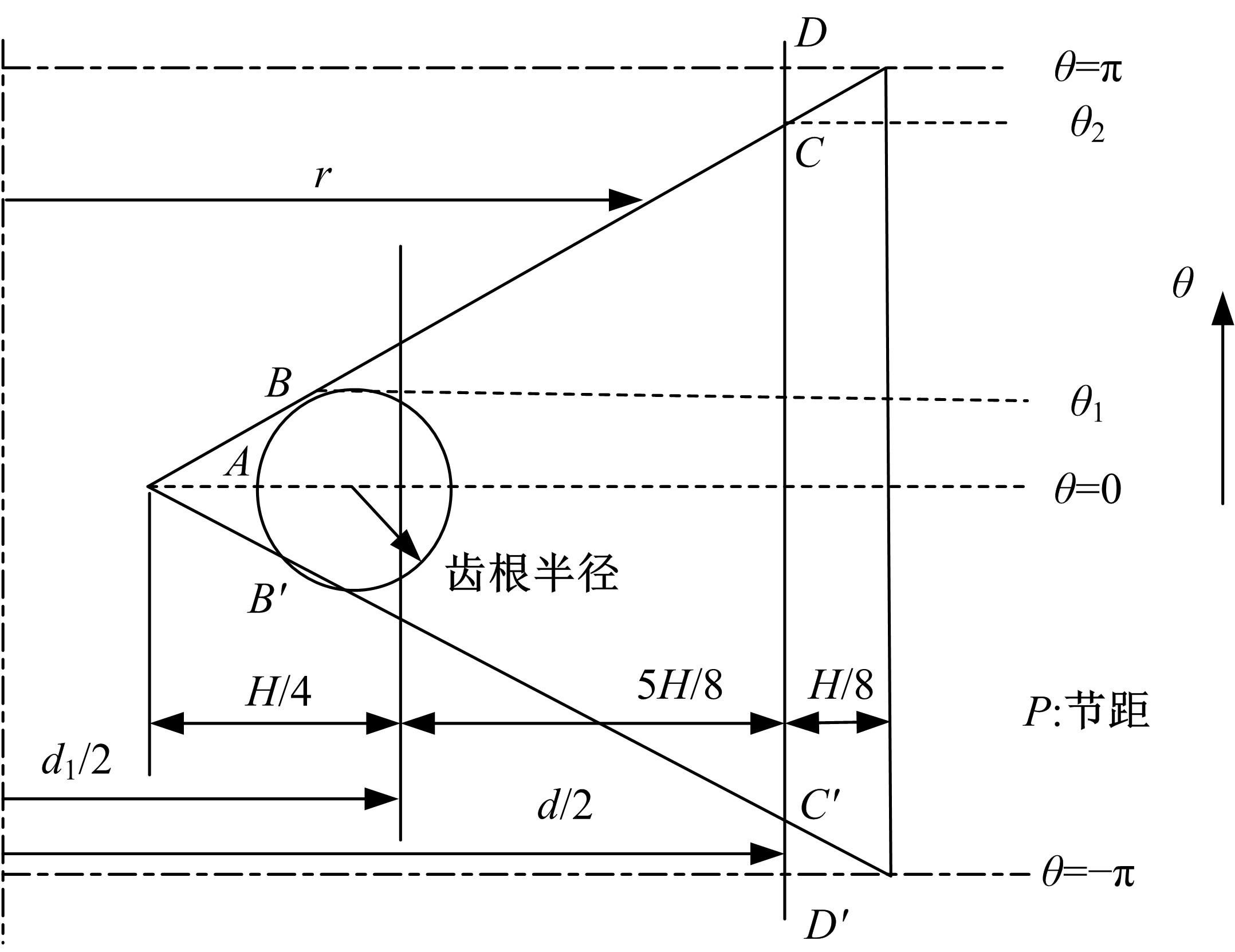
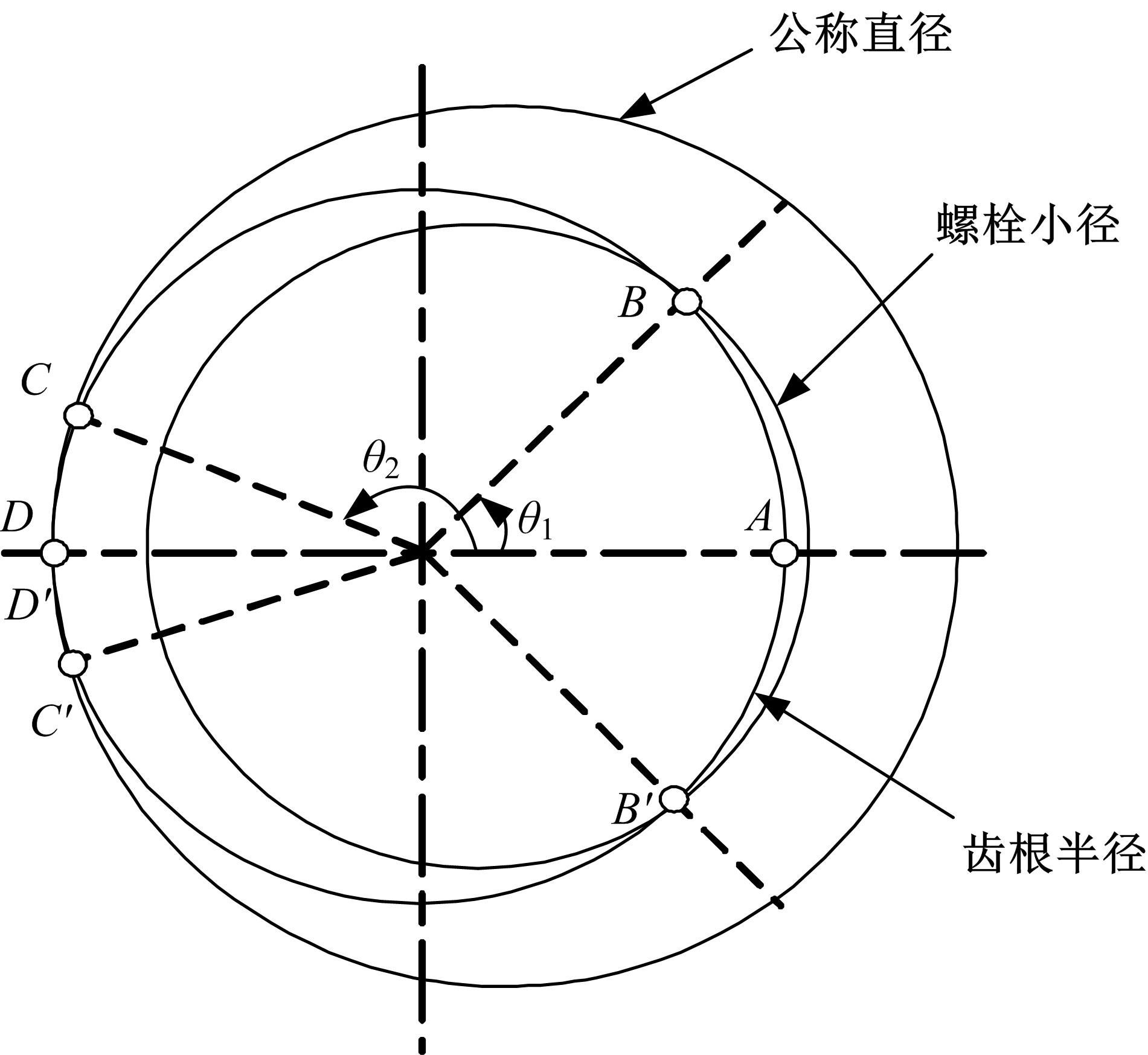
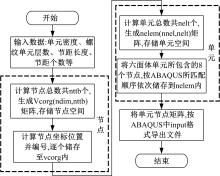
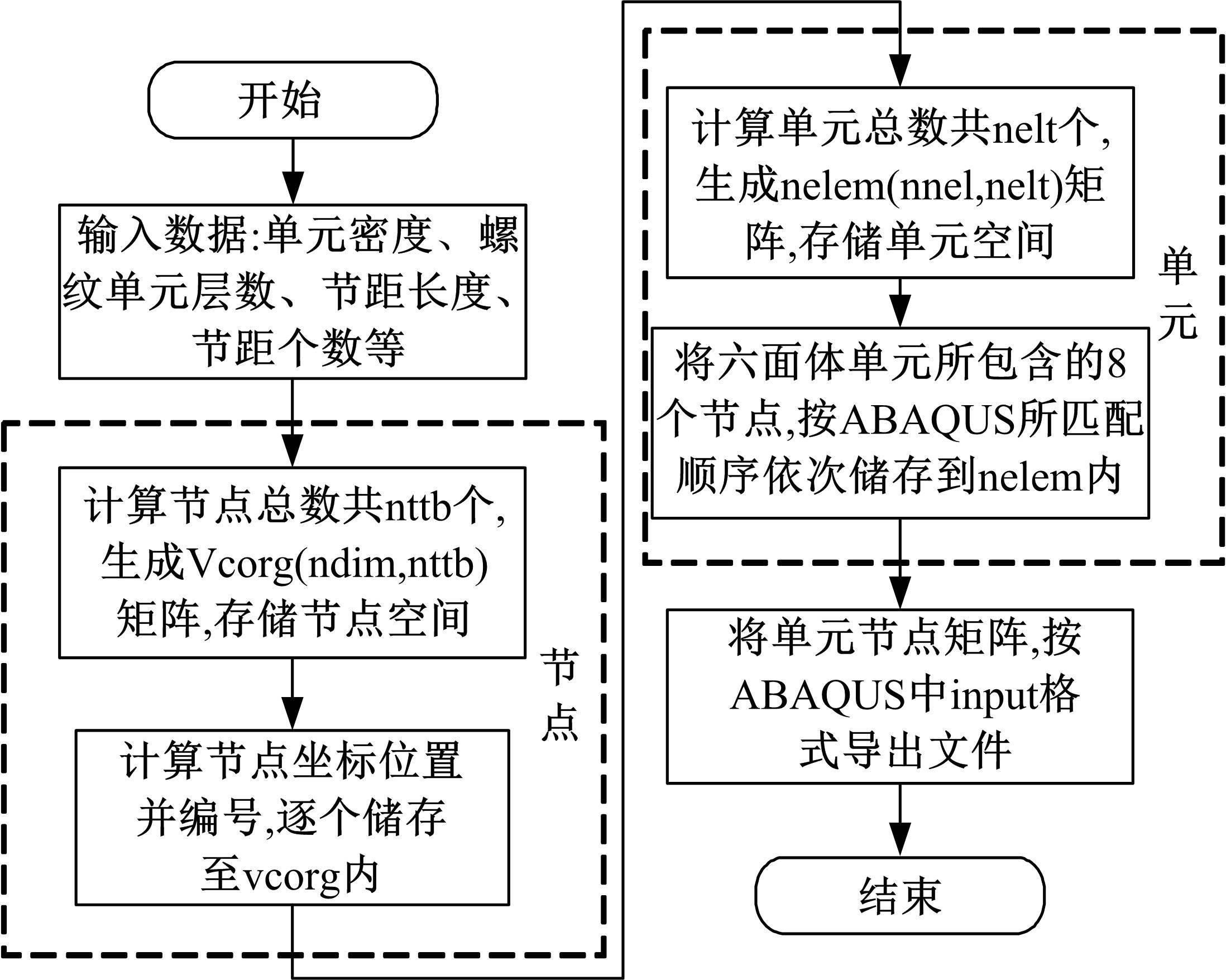
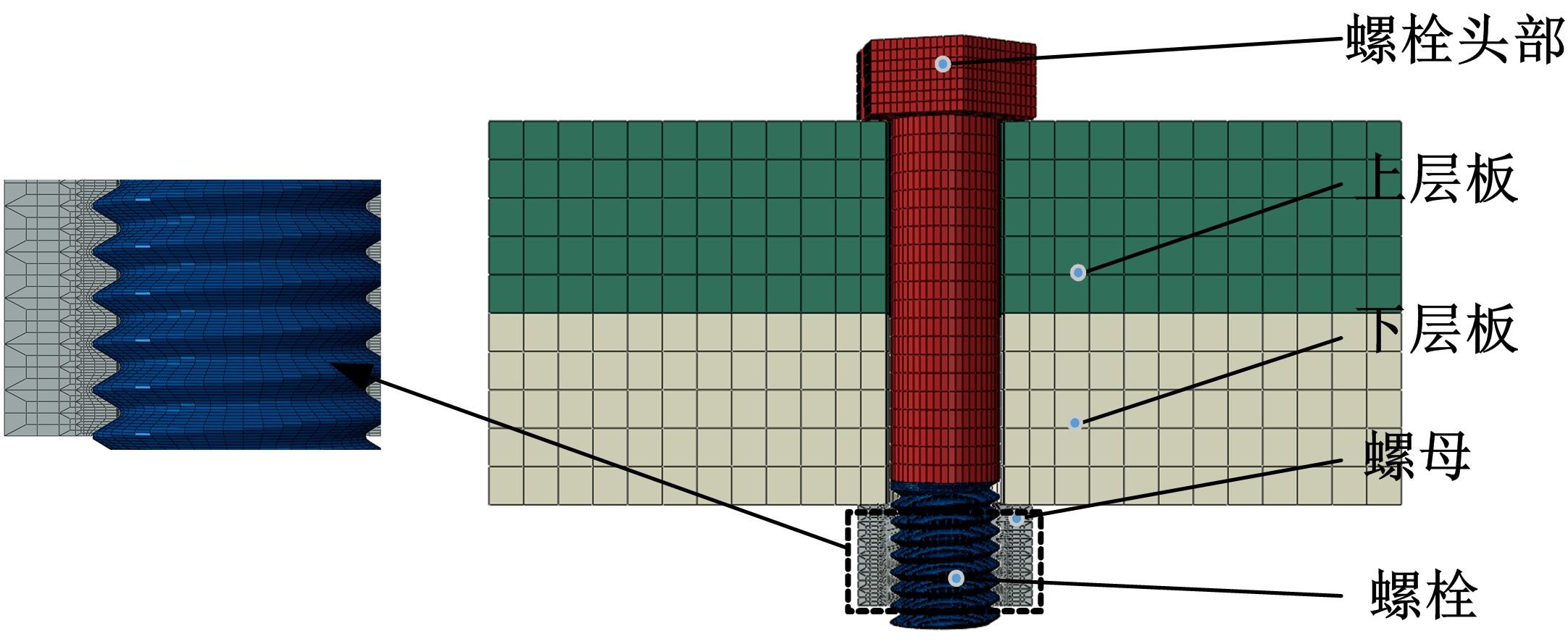
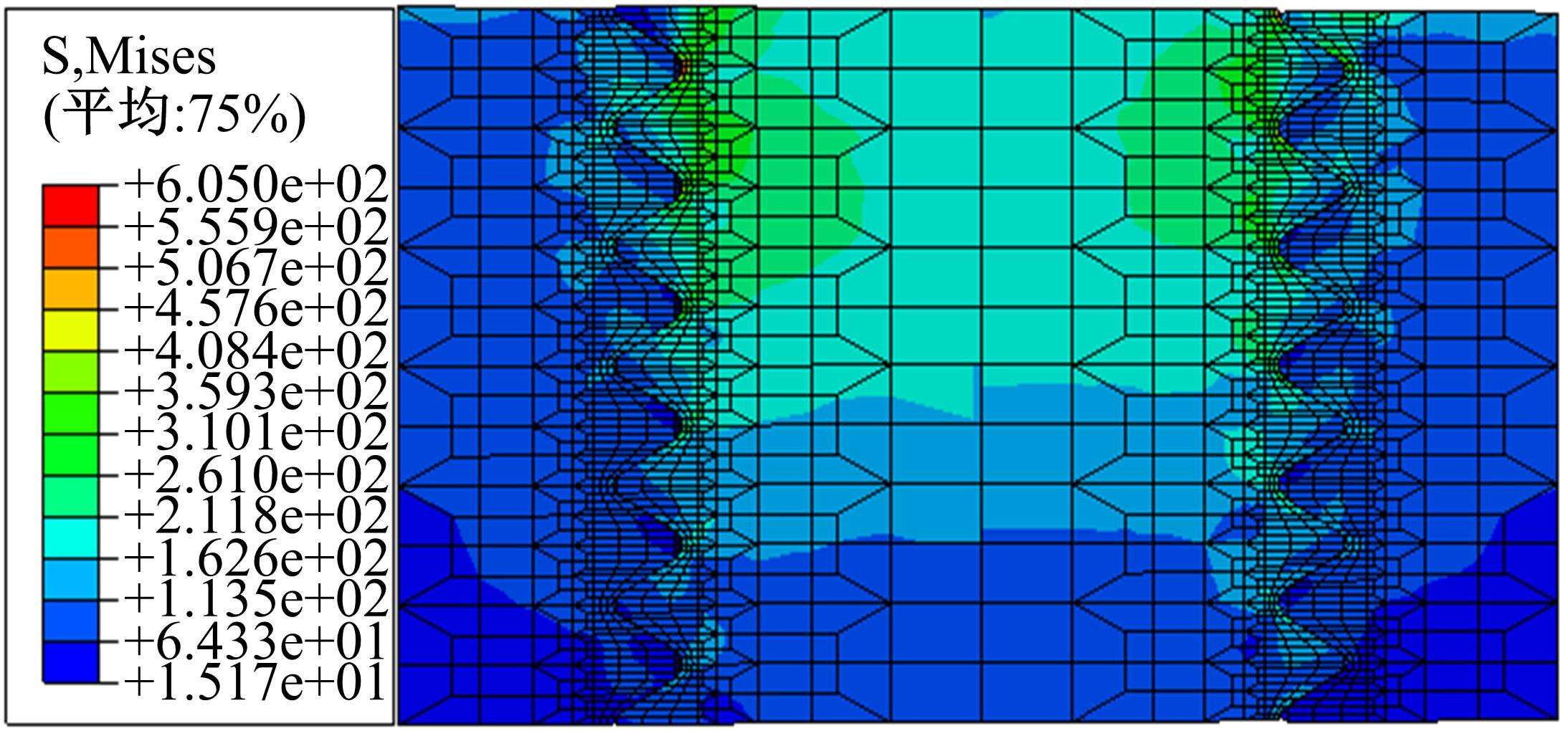
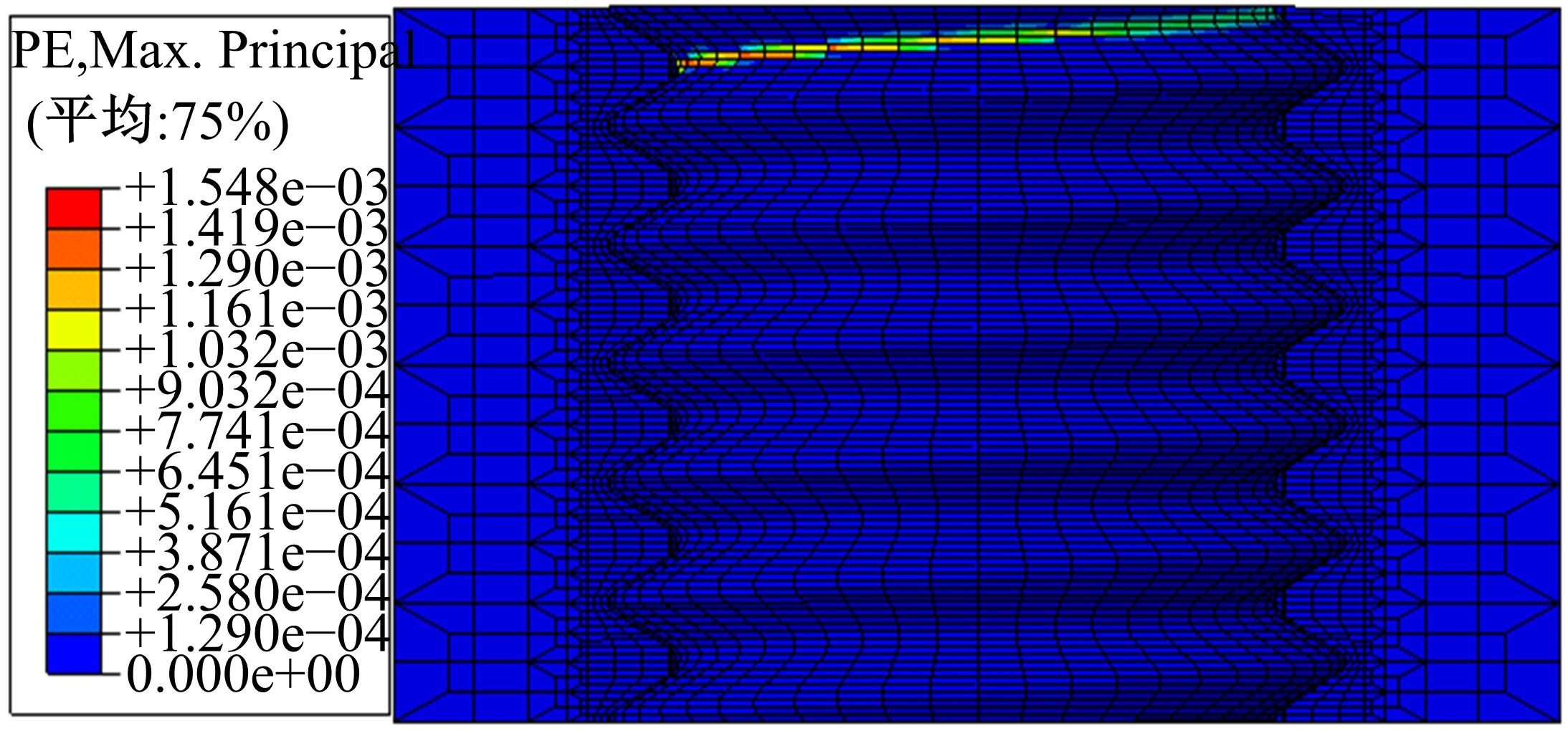
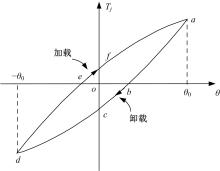
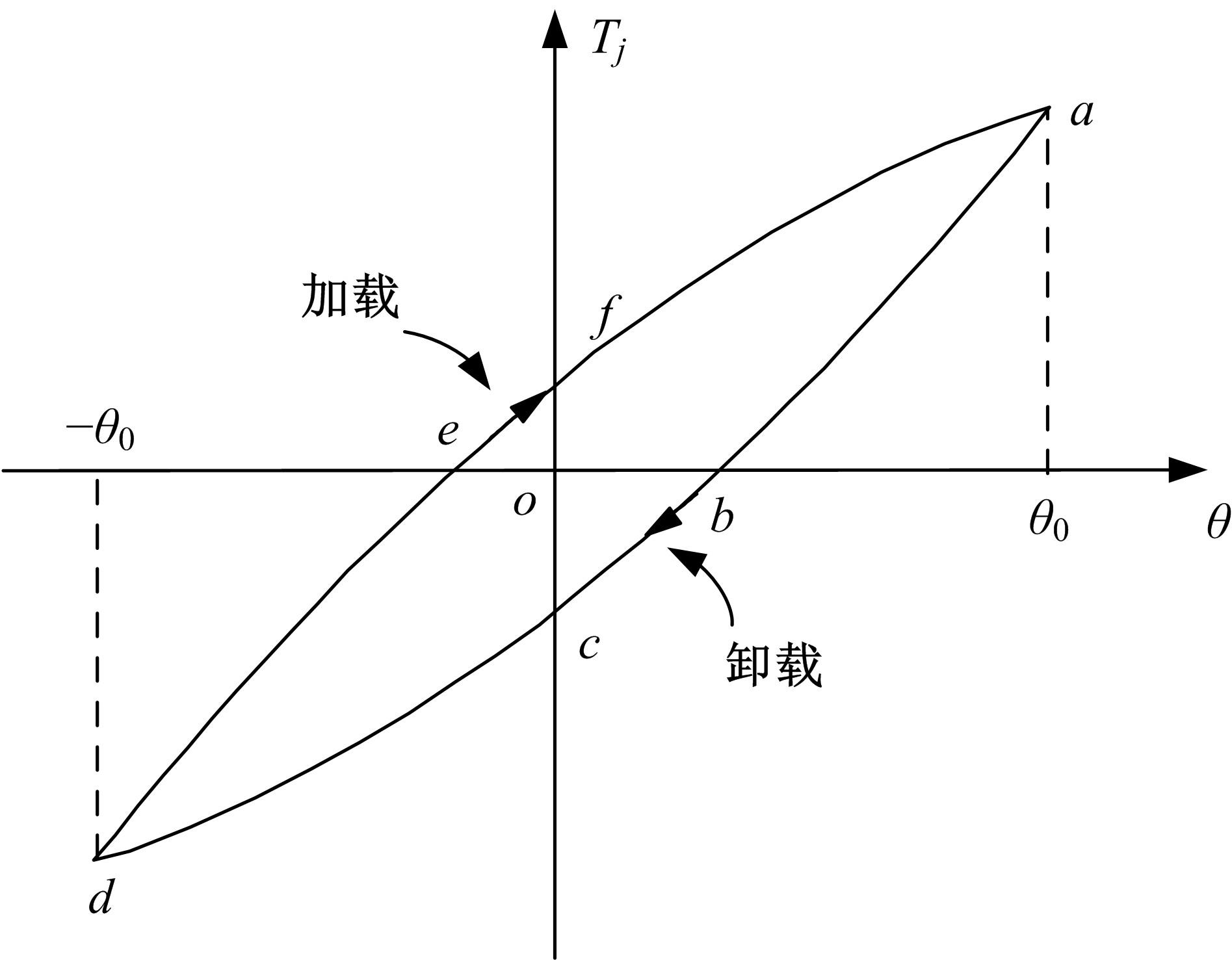
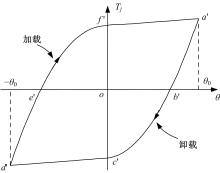
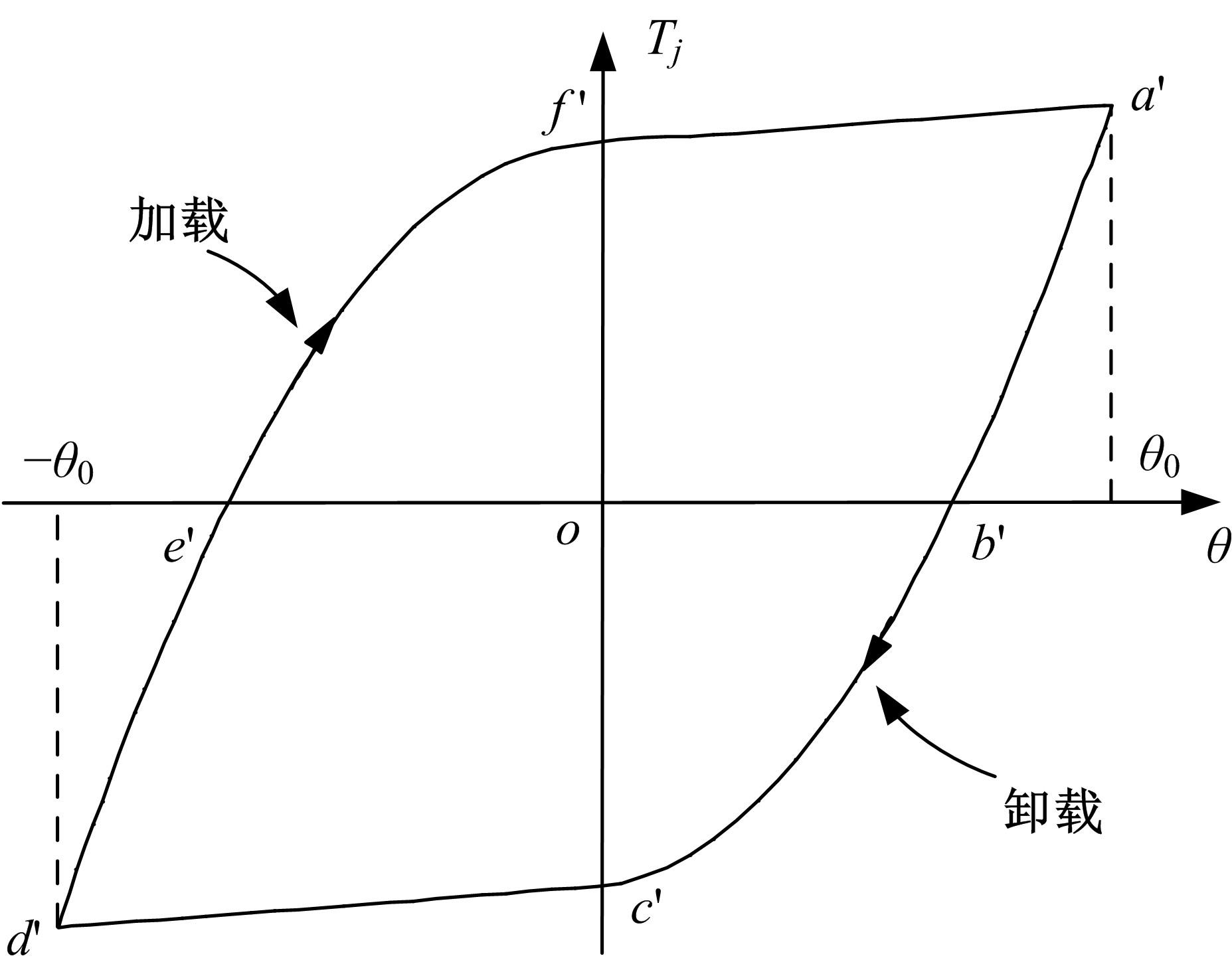
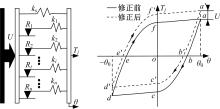
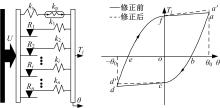
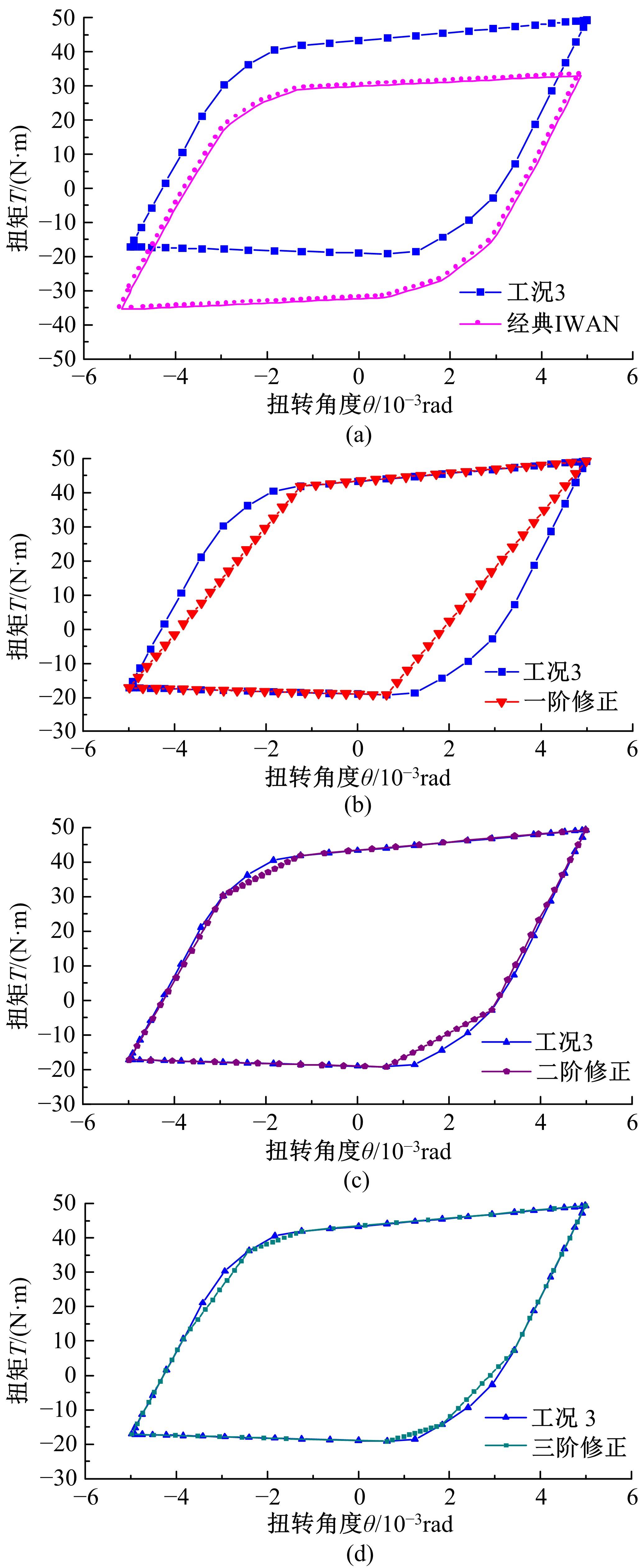
建立了螺旋形螺纹三维有限元模型，通过螺纹表面应力分布等数值计算验证模型方案的有效性，并对扭转载荷下螺纹结构的力学特性开展数值研究。结果表明：螺纹结构在加、卸载阶段均经历了黏着、部分滑移和宏观滑移3种状态；在拧紧过程的宏观滑移阶段由于轴向力增大，扭矩呈上升趋势，在拧松过程中由于轴向力减小，扭矩呈下降趋势。在螺纹结构有限元计算结果的基础上，针对扭转载荷作用下带升角的三维螺纹结构，通过增添宏观滑移时的残余刚度和扭矩整体修正量，建立了修正的IWAN模型。计算结果表明：修正的IWAN模型能较准确地重现有限元模拟结果中扭矩与转角的关系，且3个Jenkins单元模型组成的修正IWAN模型即可足够精确地还原有限元模拟得到的耗散能。

关键词: 工程力学, 螺纹结构, 有限元建模, 扭转载荷, IWAN模型

Abstract:

A three-dimensional finite element model of spiral thread is established in the paper， and the effectiveness of the model scheme is verified by the numerical calculations of "stress distribution on the surface of thread"， the mechanical properties of threaded structure under torsional load are numerically studied. The results show that： The thread structure experiences three states： adhesion， partial slip and macro slip in the loading and unloading stages； In the macro sliding stage of the tightening process， the torque increases due to the increase of axial force， and decreases due to the decrease of axial force in the loosening process. Based on the finite element calculation results of threaded structure， for the three-dimensional threaded structure with lifting angle under torsional load， the modified IWAN model is established by adding the overall correction of residual stiffness and torque during macro slip. The calculation results show that the modified IWAN model can accurately reproduce the relationship between torque and rotation angle in the finite element simulation results， The modified IWAN model composed of three Jenkins element models can accurately restore the dissipated energy obtained by finite element simulation.

Key words: engineering mechanics, thread structure, finite element modeling, torsional load, IWAN model

中图分类号:

TH112

李九一,周丰峻,刘建华,孙云厚,朱精忠,邱明坤. 扭转荷载下螺旋形螺纹连接件的IWAN改进模型[J]. 吉林大学学报(工学版), 2023, 53(5): 1305-1314.

Jiu-yi LI,Feng-jun ZHOU,Jian-hua LIU,Yun-hou SUN,Jing-zhong ZHU,Ming-kun QIU. Modified IWAN model of helical threaded connector imposed to torsional load[J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(5): 1305-1314.

图/表 17

图1

图2

图3

图4

图5

表1

表2

图6

图7

表3

图8

图9

图10

图11

图12

表4

不同数量Jenkins单元模型参数提取结果"

滞回曲线类型	k_i	R_i	单周期耗散能/J
有限元模拟	/	/	451.34
经典IWAN	/	/	453.26
1阶修正	k₁=15.70	R₁=68.50	367.04
2阶修正	k₁=23.09	R₁=52.06	438.58
2阶修正	k₂=6.90	R₂=16.43	438.58
3阶修正	k₁=26.81	R₁=42.03	440.10
	k₂=13.65	R₂=21.60
	k₃=4.01	R₃=4.87
公共修正项	k_s=0.64；U=12.179 15 N $?$ m；k_p=0.55

表4

图13

参考文献 24

1	侯世远, 廖日东. 螺纹联接松动过程的研究现状与发展趋势[J]. 强度与环境, 2014(2): 39-52.
	Hou Shi-yuan, Liao Ri-dong. Research progress on self-loosening of threaded fasteners[J]. Structure and Environment Engineering, 2014(2): 39-52.
2	Fukuoka T, Nomura M. Proposition of helical thread modeling with accurate geometry and finite element analysis[J]. ASME Journal of Pressure Vessels and Piping Technology, 2008, 130(1): 011204.
3	Hess D P, Basava S, Rasquinha I A. Variation of clamping force in a single-bolt assembly subjected to axial vibration[J]. Journal of Mechanical Design, 1996, 90(1): 97-102.
4	施刚, 石永久, 王元清. 钢结构梁柱连接节点域剪切变形计算方法[J]. 吉林大学学报: 工学版, 2006,36(4): 462-466.
	Shi Gang, Shi Yong-jiu, Wang Yuan-qing. Calculational method of shear deform action for beam-to-column connection panel zone in steel frames[J]. Journal of Jilin University(Engineering and Technology Edition), 2006, 36(4): 462-466.
5	庄蔚敏, 赵文增, 解东旋, 等. 超高强钢/铝合金热铆连接接头性能[J]. 吉林大学学报: 工学版, 2018, 48(4): 1016-1022.
	Zhuang Wei-min, Zhao Wen-zeng, Xie Dong-xuan, et al. Joint performance analysis on connection of ultrahigh-strength steel and aluminum alloy with hot riveting[J]. Journal of Jilin University(Engineering and Technology Edition), 2018, 48(4): 1016-1022.
6	Junker H G. Criteria for self loosening of fasteners under vibration[J]. Aircraft Engineering and Aerospace Technology, 1972, 44(10): 14-16.
7	Jiang Y, Chang J, Lee C H. An experimental study of the torque-tension relationship for bolted joints[J]. International Journal of Materials and Product Technology, 2001, 16(4/5): 417-429.
8	Liu J H, Ouyang H J, Feng Z Q. Study on self-loosening of bolted joints excited by dynamic axial load[J]. Tribology International, 2017, 115: 432-451.
9	Liu J H, Ouyang H J, Ma L J. Numerical and theoretical studies of bolted joints under harmonic shear displacement[J]. Latin American Journal of Solids and Structures, 2015, 12(1): 115-132.
10	Wriggers P. Computational Contact Mechanics[M]. Berlin: Wiley, 2002.
11	van Basshuysen R, Schäfer F. Internal Combustion Engine Handbook: Basics, Components, Systems, and Perspectives[M]. Warrendale: SAE International, 2004.
12	Gaul L, Nitsche R. The role of friction in mechanical joints[J]. Applied Mechanics Reviews, 2001, 54: 93-106.
13	Gaul L, Lenz J. Nonlinear dynamics of structures assembled by bolted joints[J]. Acta Mechanica, 1997, 125(1): 169-181.
14	Liu J H, Ouyang H J. Dynamic behaviour of a bolted joint subjected to torsional excitation[J]. Tribology International, 2019, 140: 105877.
15	Valanis K C. Fundamental consequences of a new intrinsic time measure: plasticity as a limit of the endochronic theory[J]. Archiwum Mechaniki Stossowanej, 1980, 32(2): 171-191.
16	Ikhouane F, Hurtado J E, Rodellar J. Variation of the hysteresis loop with the Bouc-Wen model parameters[J]. Nonlinear Dynamics, 2007, 48(4): 361-380.
17	Wen Y K. Methods of random vibration for inelastic structures[J]. Applied Mechanics Reviews, 1989, 42(2): 39-52.
18	Iwan W D, A distributed-element model for hysteresis and its steady-state dynamic response[J]. Journal of Applied Mechanics, 1966, 33(4): 893-900.
19	张相盟, 王本利, 卫洪涛. Iwan模型非线性恢复力及能量耗散计算研究[J]. 工程力学, 2012, 29(11): 33-39.
	Zhang Xiang-meng, Wang Ben-li, Wei Hong-tao. Calculation of nonlinear restoring forces and energy dissipation of Iwan model[J]. Engineering Mechanics, 2012, 29(11): 33-39.
20	Iwan W D. On a class of models for the yielding behavior of continuous and composite systems[J]. Journal of Applied Mechanics, 1967, 34(3): 612-617.
21	全国螺纹标准化技术委员会. 公制、美制和英制螺纹标准手册[M]. 3版. 北京: 中国标准出版社, 2009.
22	Eramo M D, Cappa P. An experimental validation of load distribution in screw threads[J]. Experimental Mechanics, 1991, 31(1): 70-75.
23	濮良贵, 陈国定, 吴立言. 机械设计[M]. 9版. 北京: 高等教育出版社, 2013.
24	Segalman D J, Starr M J. Inversion of masing models via continuous Iwan systems[J]. International Journal of Non-linear Mechanics, 2008, 43(1): 74-80.

相关文章 15

[1]	孟广伟,任传鑫,李锋,魏彤辉. 随机载荷作用下的结构疲劳寿命区间分析[J]. 吉林大学学报(工学版), 2022, 52(1): 46-52.
[2]	李碧雄,廖桥,章一萍,周练,隗萍,刘侃. 超高强钢筋工程用水泥基复合材料梁受弯计算理论[J]. 吉林大学学报(工学版), 2019, 49(4): 1153-1161.
[3]	尼颖升,孙启鑫,马晔,徐栋,刘超. 基于空间网格分析的多箱室波形钢腹板组合梁腹板剪力分配[J]. 吉林大学学报(工学版), 2018, 48(6): 1735-1746.
[4]	闫亚宾, 王晓媛, 万强. 纳米尺度界面低周疲劳破坏行为[J]. 吉林大学学报(工学版), 2017, 47(4): 1201-1206.
[5]	陈江义, 刘保元. 纤维断裂损伤对复合材料板中导波频散特性的影响[J]. 吉林大学学报(工学版), 2017, 47(1): 180-184.
[6]	孟广伟, 冯昕宇, 周立明, 李锋. 基于降维算法的结构可靠性分析[J]. 吉林大学学报(工学版), 2017, 47(1): 174-179.
[7]	庄晔, 陈禹行, 杨业海, 徐淑芳. 某双筒液阻式减振器外特性建模[J]. 吉林大学学报(工学版), 2016, 46(3): 732-736.
[8]	杨慧艳, 何晓聪, 周森. 压印接头强度的有限元模型及理论计算方法[J]. 吉林大学学报(工学版), 2015, 45(3): 864-871.
[9]	张庆, 王磊. 基于微分方程组的多排桩内力分析[J]. 吉林大学学报(工学版), 2014, 44(5): 1327-1333.
[10]	赵世佳, 徐涛, 陈炜, 谭丽辉. 接近亏损系统模态灵敏度分析的有效算法[J]. 吉林大学学报(工学版), 2013, 43(增刊1): 497-499.
[11]	徐涛, 赵世佳, 张炜, 谭丽辉, 吕岗, 李恒. N重亏损系统摄动的原点移位组合近似方法[J]. 吉林大学学报(工学版), 2012, 42(增刊1): 147-150.
[12]	闫光, 范舟, 李钟海, 程小全, 刘克格, 左春柽. 复合材料加口盖柱壳的设计与分析[J]. , 2012, (06): 1437-1441.
[13]	李春良^1,2,王国强¹,刘福寿³,赵凯军⁴. 盾构管片结构的力学行为分析[J]. 吉林大学学报(工学版), 2011, 41(6): 1669-1674.
[14]	张道明¹,郭学东²,赵志蒙³. 钢筋混凝土梁弯曲损伤分析的摄动法[J]. 吉林大学学报(工学版), 2011, 41(05): 1358-1363.
[15]	陈耕野, 王彦召, 姚战卫. 平行弦钢桁架应力与感应电动势随荷载的变化[J]. 吉林大学学报(工学版), 2010, 40(增刊): 222-0227.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

部件（材料）	密度/ （kg·m^-3）	弹性模量 /MPa	泊松比
螺栓（35CrMn）	7.87	213 000	0.286
螺母（45钢）	7.87	209 000	0.269
板（碳钢）	7.87	210 000	0.280

螺栓（35CrMn）		螺母（45钢）
应力/MPa	塑性应变	应力/MPa	塑性应变
480	0	400	0
500	0.002 82	420	0.001 52
580	0.012	500	0.0295
680	0.045	630	0.056
850	0.11	700	0.095
1000	0.3	760	0.25