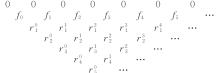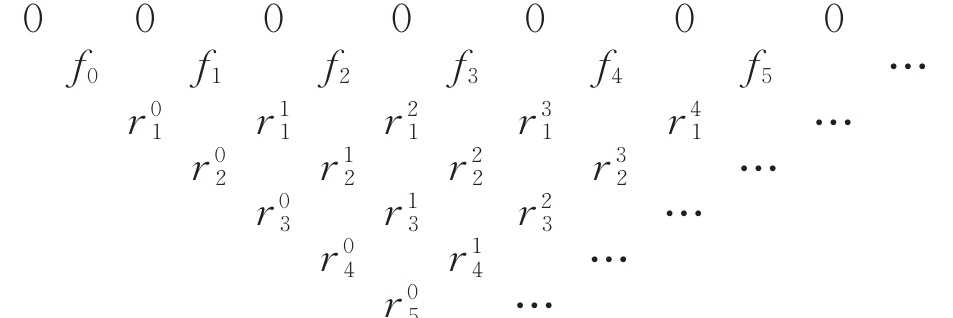吉林大学学报(工学版) ›› 2025, Vol. 55 ›› Issue (1): 74-83.doi: 10.13229/j.cnki.jdxbgxb.20230333
基于投影优选法的结构静态位移多目标优化方法
- 吉林大学 机械与航空航天工程学院,长春 130022
Multi-objective optimization method of structural static displacement based on projection priority selection method
Kai MA( ),Jian-hang SUN,Sen-kang YAN,Yan TAO,Wen-tao WANG,Gui-kai GUO(
),Jian-hang SUN,Sen-kang YAN,Yan TAO,Wen-tao WANG,Gui-kai GUO( )
)
- School of Mechanical and Aerospace Engineering,Jilin University,Changchun 130022,China
摘要:
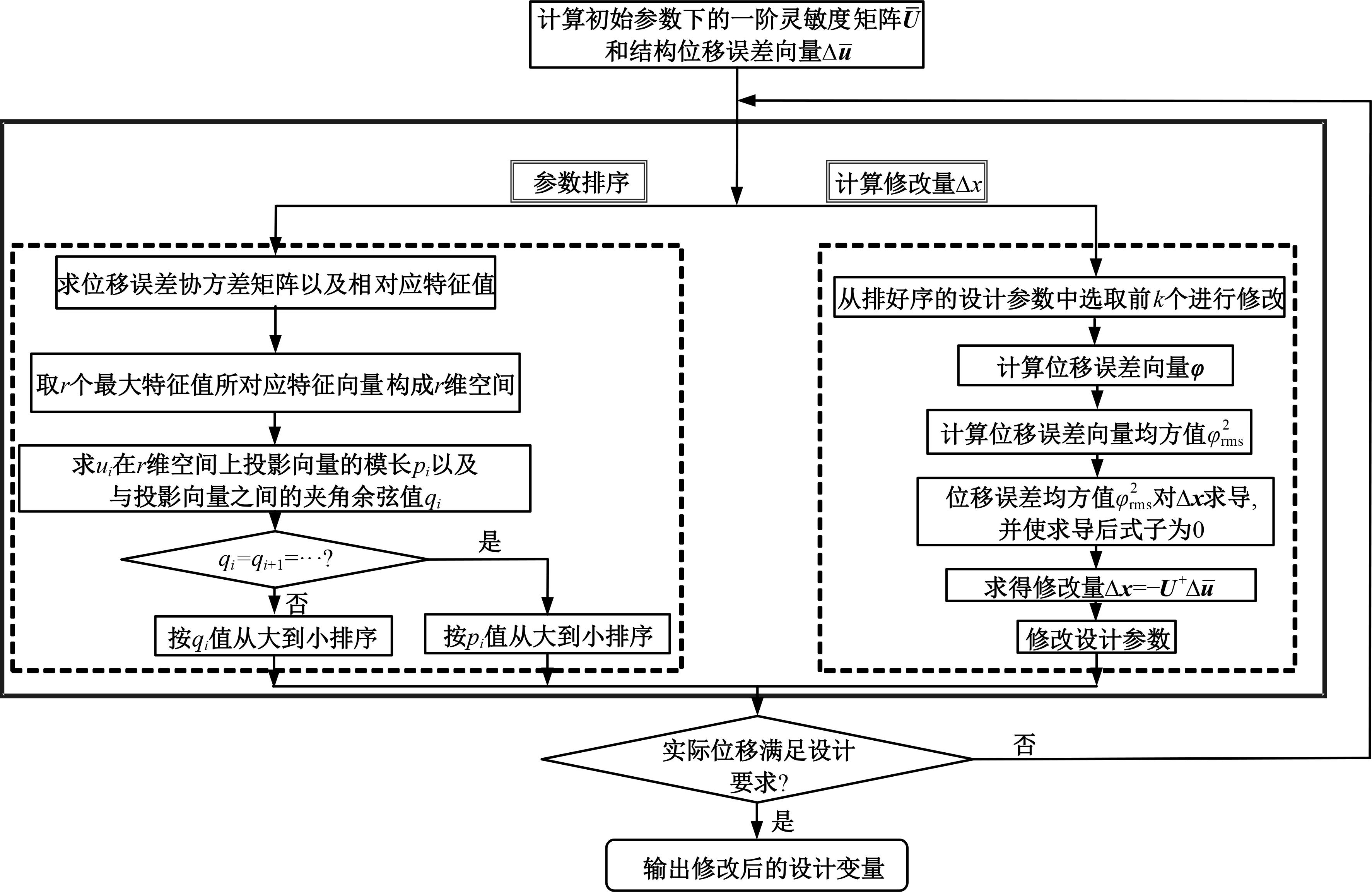
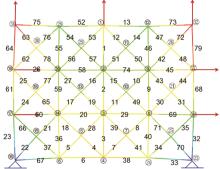
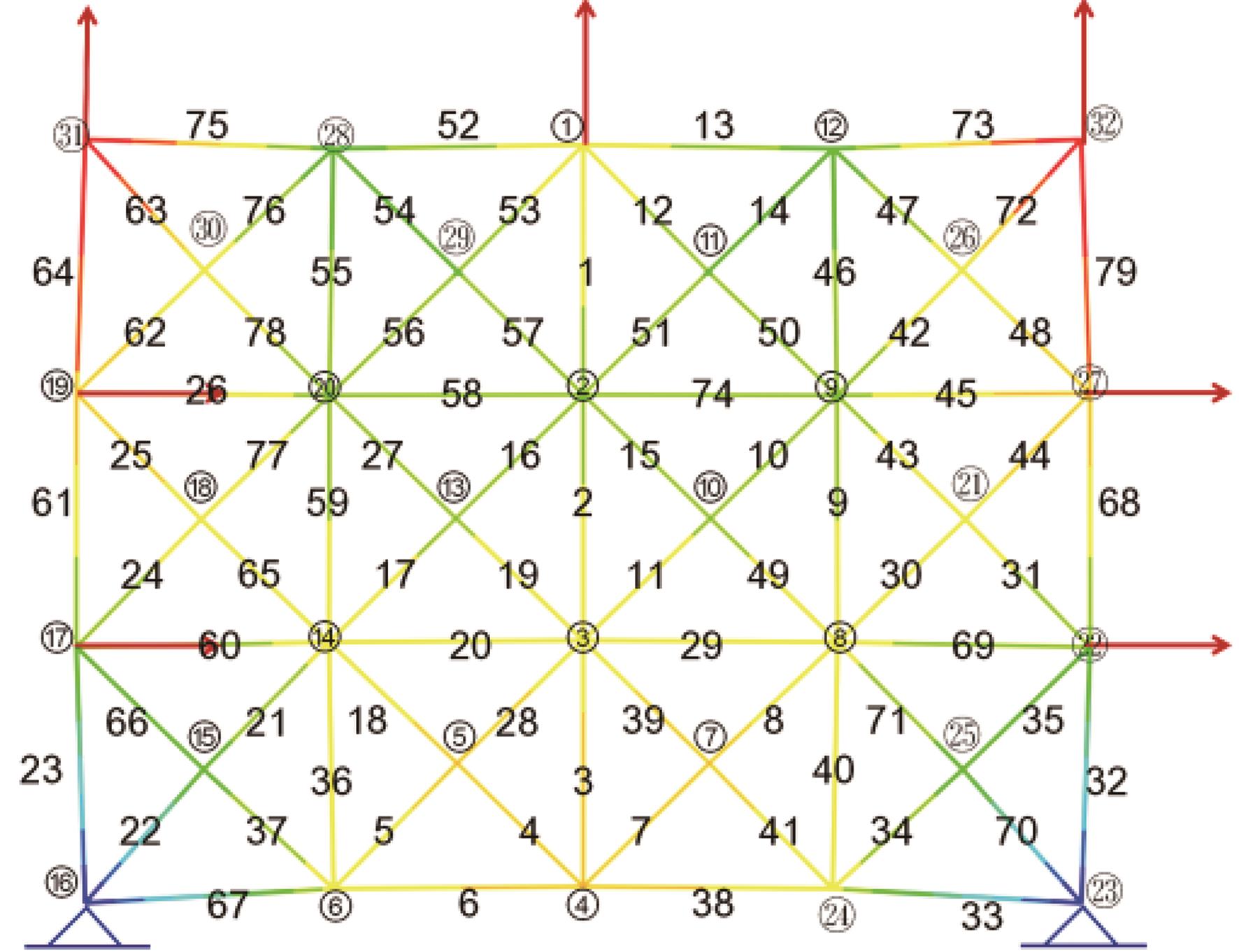
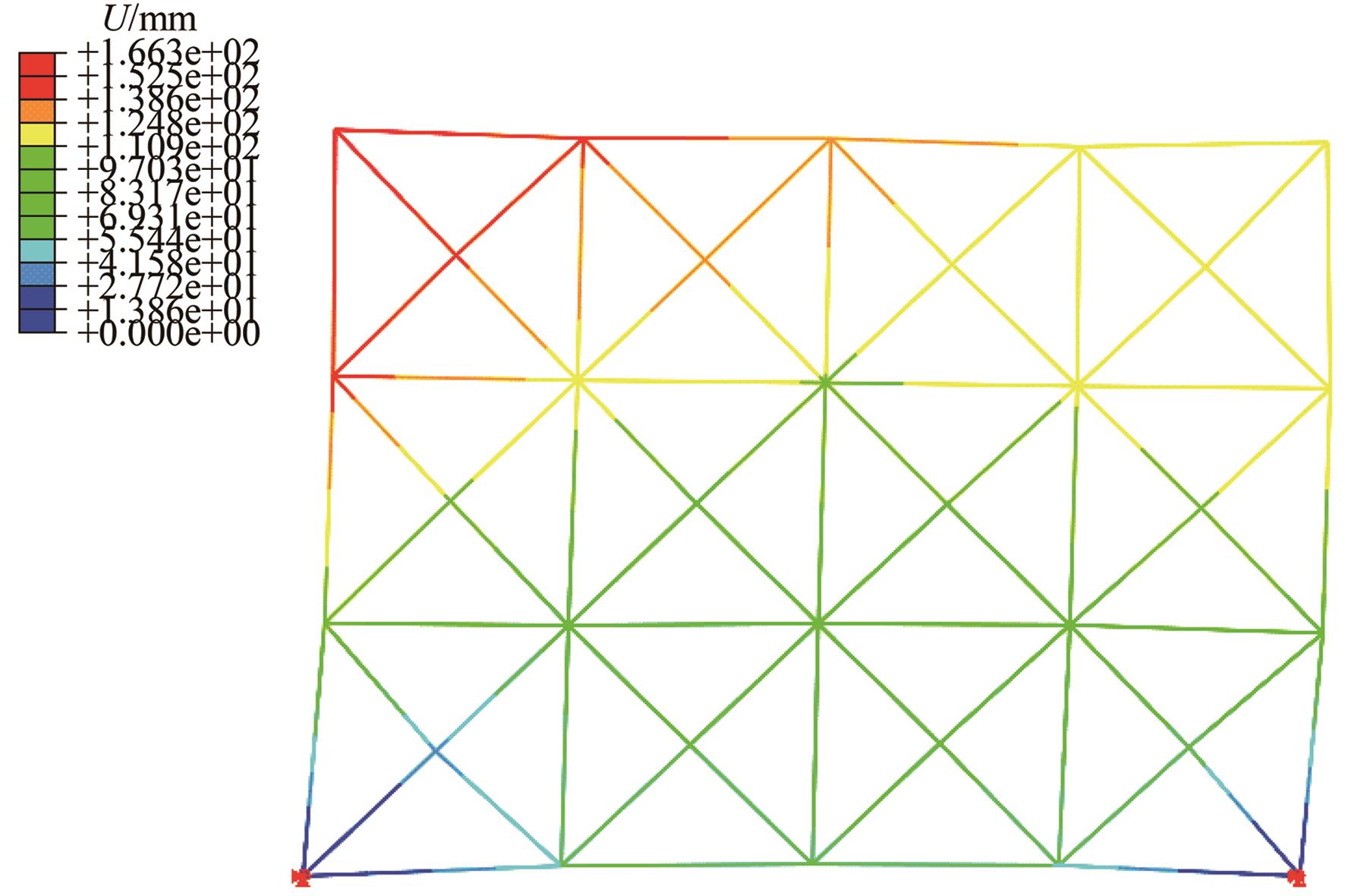
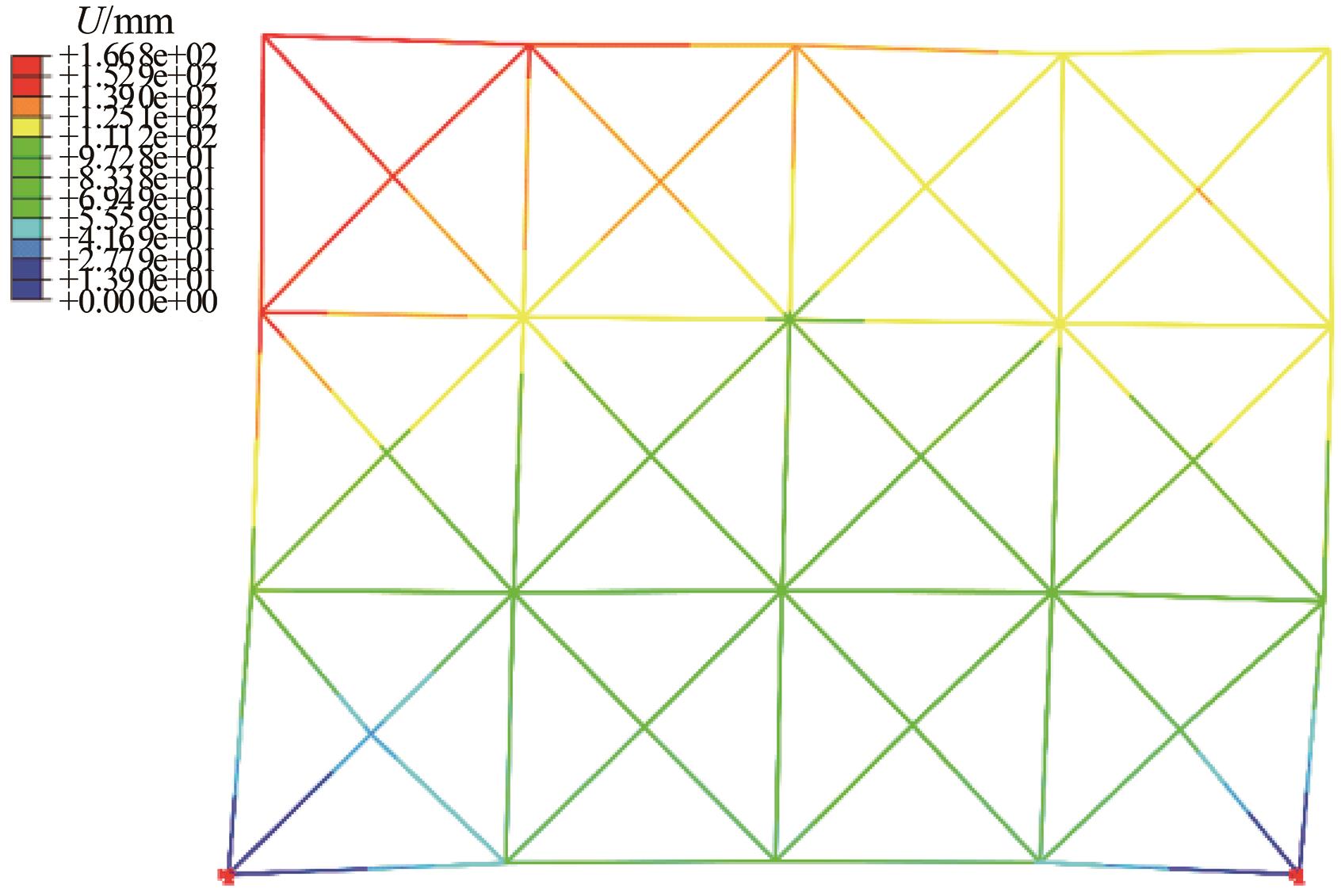
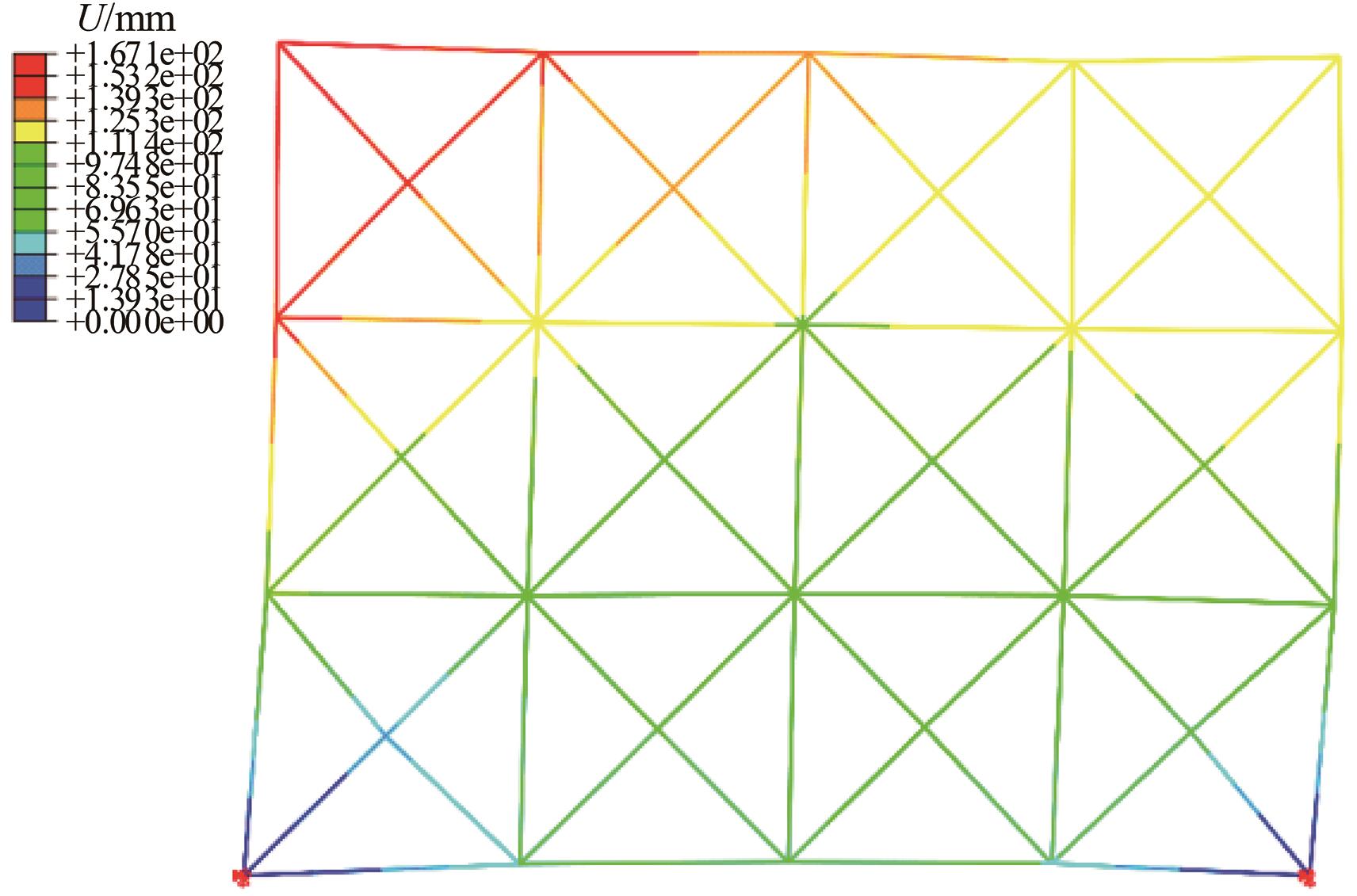
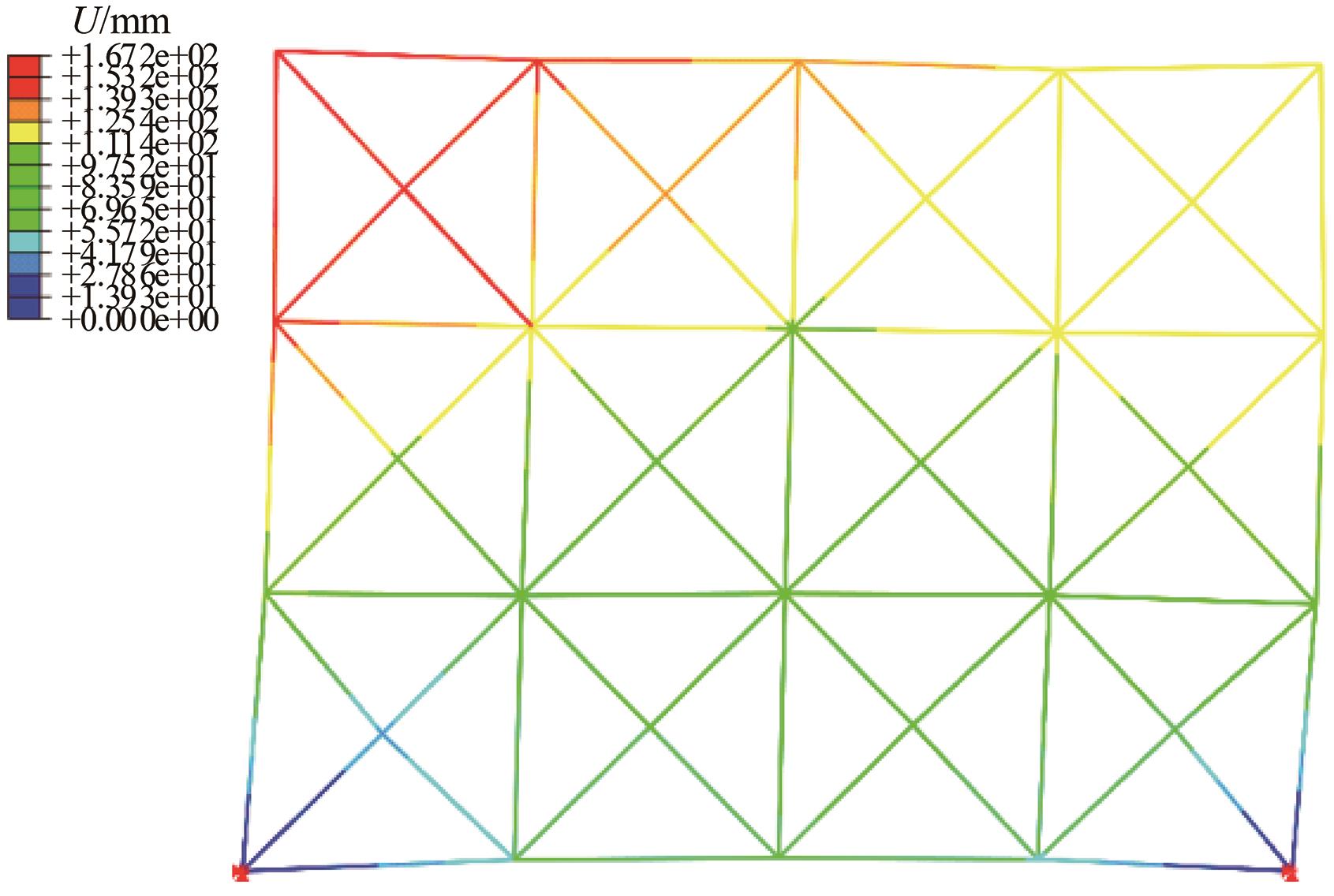
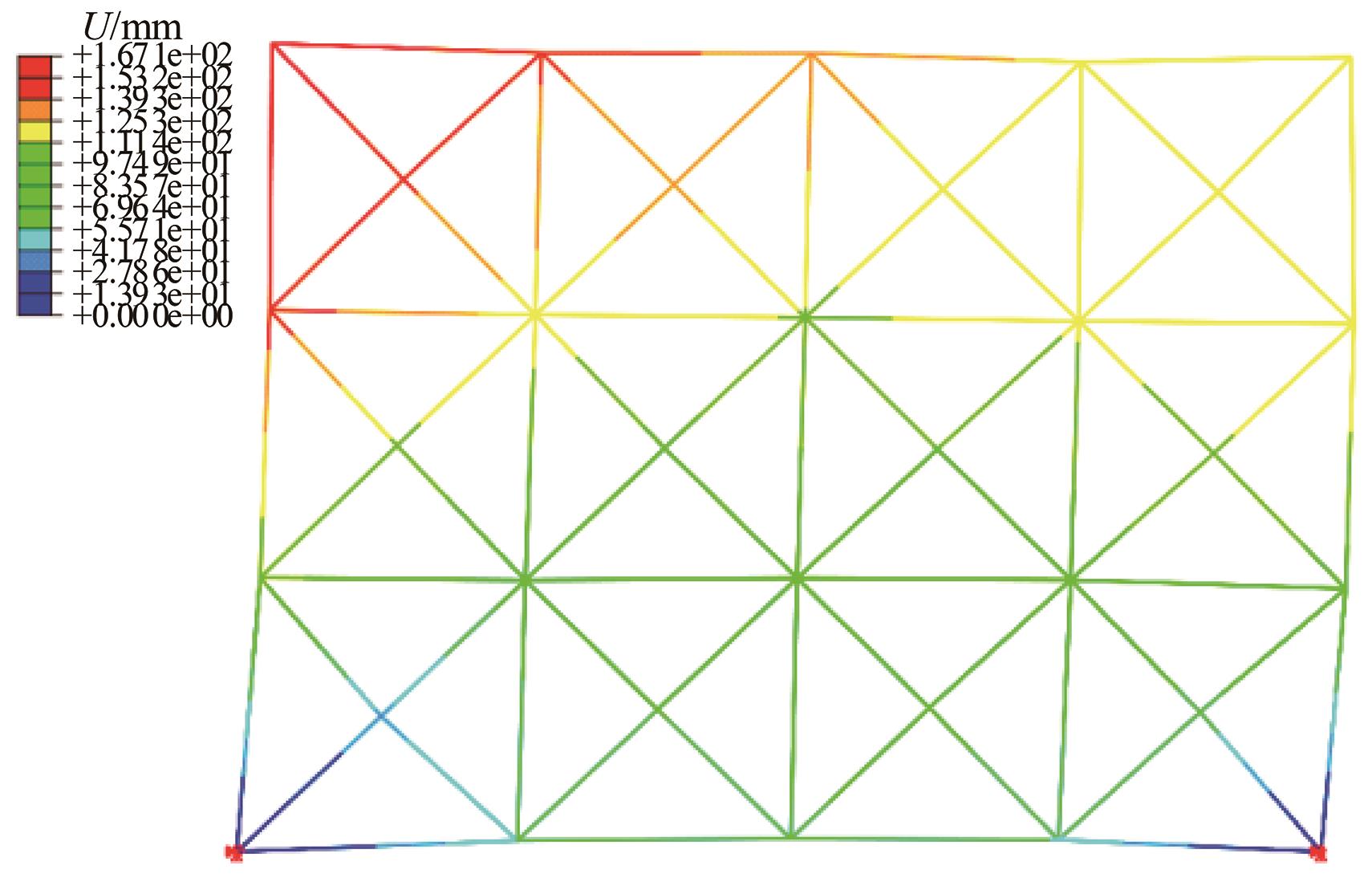
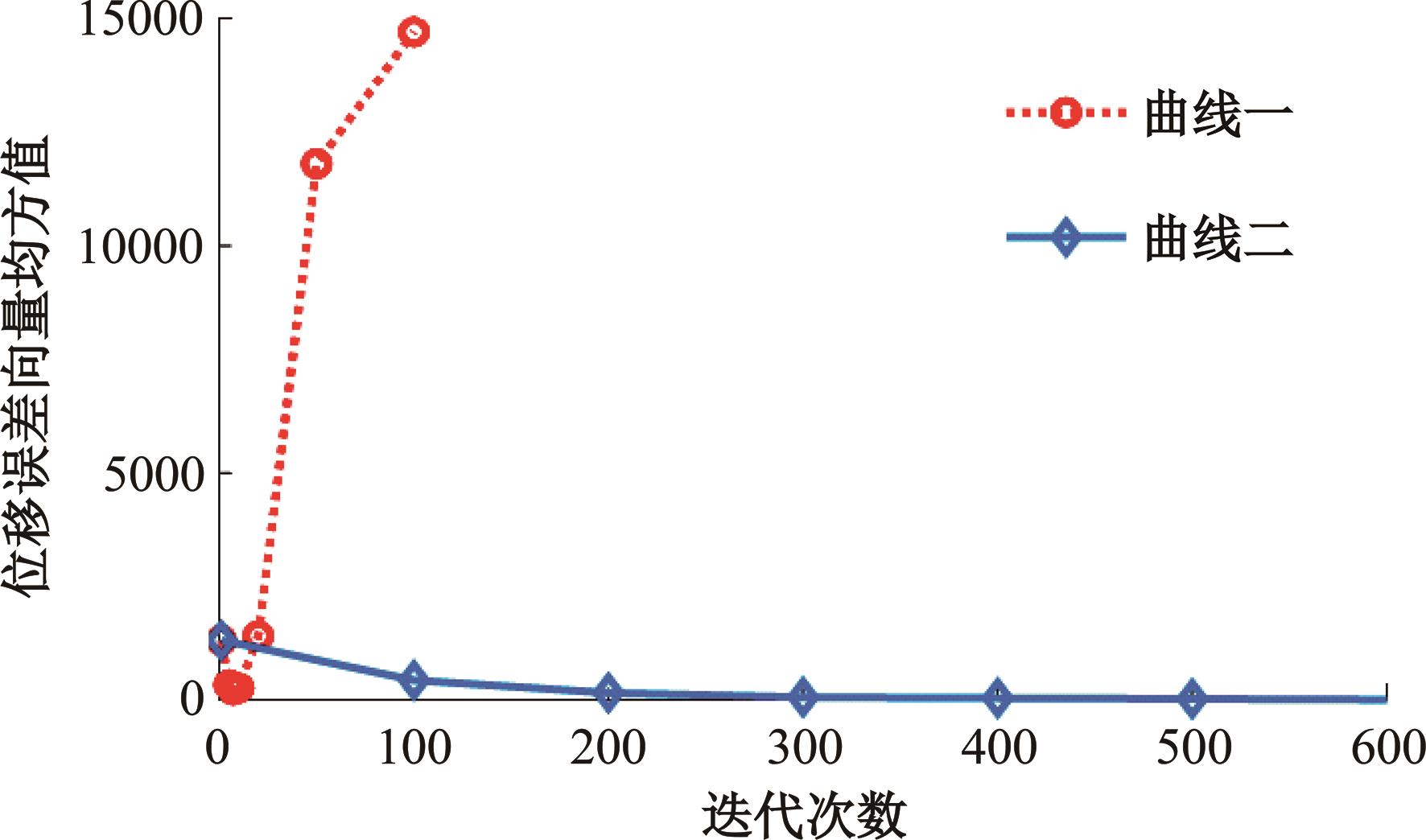
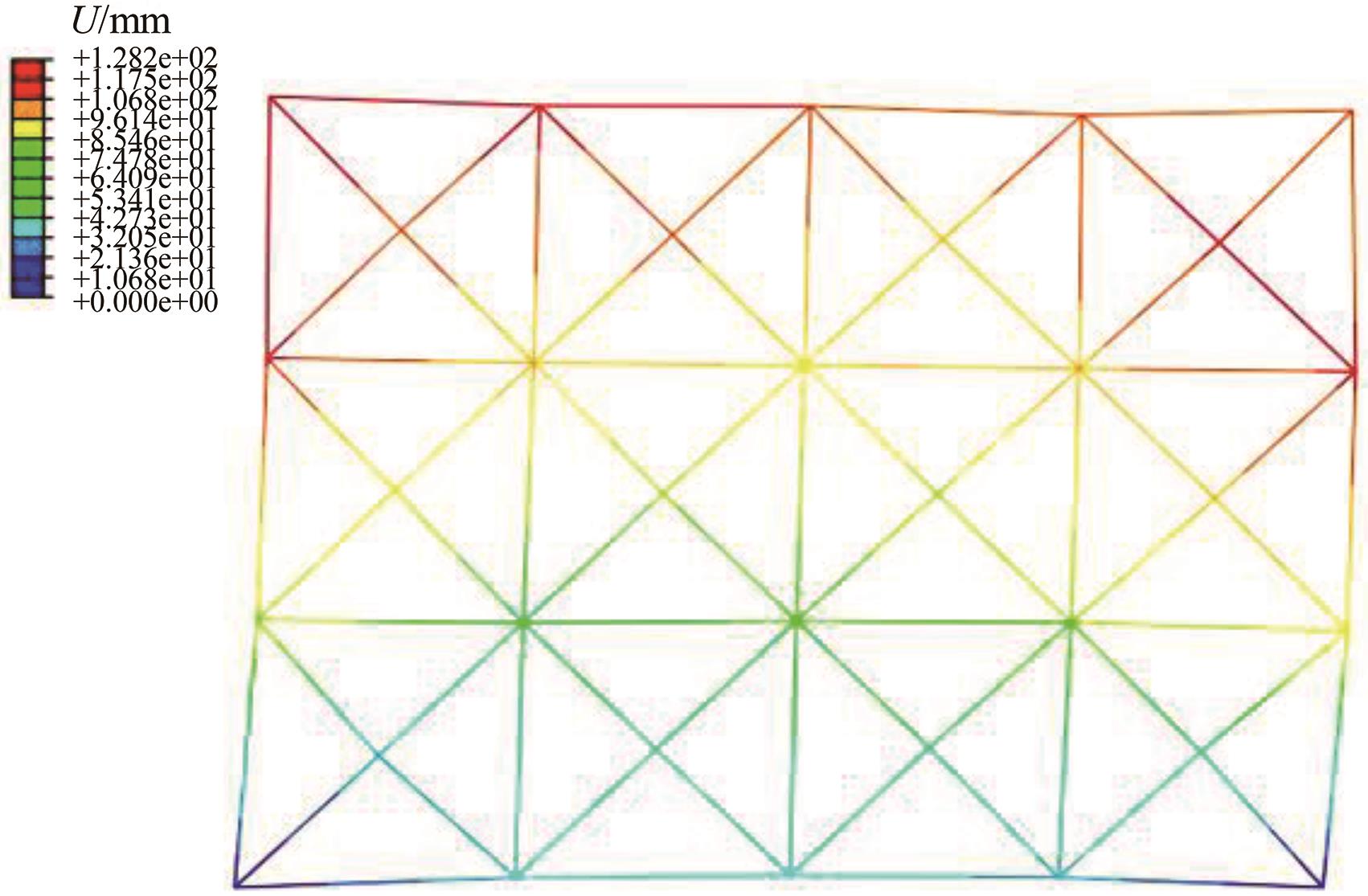
本文提出了一种基于投影优选法的结构静态位移多目标优化方法。投影优选法是根据参数灵敏度向量在特定的多维子空间的投影角度和投影长度来对参数进行排序的参数选取方法。其中,本文采用的结构静态灵敏度的解析计算方法是结合Epsilon算法和改进的纽曼级数建立的。该多目标优化方法每步迭代都可按照给定的参数个数要求来选取合理的参数组合并得到对应参数的修改量,通过多次迭代计算得到优化解。该方法特别适用于限定参数个数的多目标结构优化问题。在算例中,使用该方法对一个桁架结构进行多目标优化。算例中还用随机选取的参数组与本文方法选定的参数组做优化结果对比。对比结果表明:应用本文方法的优化结果更理想。算例进一步证明了本文优化方法具有很高的工程应用价值。
中图分类号:
- O342
| 1 | 宋大同, 陈塑寰, 邱志平. 结构频率误差修正参数的最优选取问题[J]. 力学学报,1995,27(1):110-116. |
| Song Da-tong, Chen Su-huan, Qiu Zhi-ping. Optimal correction of frequency errors and selection method of parameters to be modified[J]. Acta Mechanica Sinica, 1995, 27(1):110-116. | |
| 2 | 麻凯, 管欣, 李鹏. 悬架运动学特性优化中的参数选取方法[J]. 汽车工程,2013,35(6):516-520. |
| Ma Kai, Guan Xin, Li Peng. Parameter selection method in optimization of suspension kinematics characteristics[J]. Automotive Engineering, 2013, 35(6):516-520. | |
| 3 | Conte J P, Vijalapura P K, Meghella M. Consistent finite-element response sensitivity analysis[J]. Journal of Engineering Mechanics, 2003, 129(12): 1380-1393. |
| 4 | 李莎, 肖南, 董石麟. 变长度单元自适应索杆张力结构响应灵敏度分析[J]. 华中科技大学学报:自然科学版,2014,42(10):119-123. |
| Li Sha, Xiao Nan, Dong Shi-lin. Sensitivity analysis on responses of adaptive cable-strut tensile structure with length changeable elements[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2014, 42(10):119-123. | |
| 5 | 刘广, 刘济科, 吕中荣. 基于时域响应灵敏度分析的非线性系统参数识别[J]. 振动与冲击,2018,37(21):213-219. |
| Liu Guang, Liu Ji-ke, Zhong-rong Lyu. Parametric recognition of a nonlinear system based on time domain response sensitivity analysis[J]. Journal of Vibration and Shock, 2018, 37(21):213-219. | |
| 6 | 黄毅, 刘辉, 项昌乐. 基于一、二阶嵌入灵敏度分析的车辆传动系统振动响应预测[J]. 振动与冲击,2015,34(6):72-78. |
| Huang Yi, Liu Hui, Xiang Chang-le. Vibration response prediction for a vehicle transmission system using first-order and second-order iterative embedded sensitivity analysis[J]. Journal of Vibration and Shock, 2015, 34(6):72-78. | |
| 7 | 邱志平, 王晓军. 结构灵敏度分析的区间方法[J]. 兵工学报,2005,26(6):80-84. |
| Qiu Zhi-ping, Wang Xiao-jun. An interval method for sensitivity analysis of the structures[J]. Acta Armamentarii, 2005, 26(6):80-84. | |
| 8 | Kiran R, Li L, Khandelwal K. Complex perturbation method for sensitivity analysis of nonlinear trusses [J]. Journal of Structural Engineering, 2017, 143(1): No.04016154. |
| 9 | Wang D. Sensitivity analysis of structural response to position of external applied load in plate flexural condition[J]. Computers & Structures, 2017, 190: 25-40. |
| 10 | Gu Q, Liu Y D, Li Y, et al. Finite element response sensitivity analysis of three-dimensional soil-foundation-structure interaction(SFSI) systems[J]. Earthquake Engineering and Engineering Vibration, 2018, 17(3): 555-566. |
| 11 | Lin L, Chang H, Zhang X. Research on beam structure damage identification method based on time domain response sensitivity analysis[J]. Journal of Physics: Conference Series, 2019, 1213(5):No. 052024. |
| 12 | Luo Z, Wang X, Liu D. Prediction on the static response of structures with large-scale uncertain-but-bounded parameters based on the adjoint sensitivity analysis[J]. Structural and Multidisciplinary Optimization, 2020, 61(1): 123-139. |
| 13 | 陈飙松, 张力丹, 鲁一南,等. 结构优化半解析灵敏度分析的改进算法[J]. 计算力学学报,2018,35(5):533-539. |
| Chen Biao-song, Zhang Li-dan, Lu Yi-nan, et al. Modified semi-analytical sensitivity analysis methods for structural design optimization[J]. Chinese Journal of Computational Mechanics, 2018, 35(5):533-539. | |
| 14 | Radau L, Gerzen N, Barthold F J. Sensitivity of structural response in context of linear and non-linear buckling analysis with solid shell finite elements[J]. Structural and Multidisciplinary Optimization, 2017, 55(6): 2259-2283. |
| 15 | Zuo W, Xu T, Zhang H, et al. Fast structural optimization with frequency constraints by genetic algorithm using adaptive eigenvalue reanalysis methods [J]. Structural and Multidisciplinary Optimization, 2011, 43(6): 799-810. |
| 16 | Zuo W, Yu Z, Zhao S, et al. A hybrid fox and kirsch's reduced basis method for structural static reanalysis[J]. Structural and Multidisciplinary Optimization, 2012, 46(2): 261-272. |
| 17 | Zuo W, Bai J, Yu J. Sensitivity reanalysis of static displacement using Taylor series expansion and combined approximate method[J]. Structural and Multidisciplinary Optimization, 2016, 53(5): 953-959. |
| 18 | 麻凯, 李邦辉, 杨坤, 等. 结构静态位移一阶和二阶灵敏度近似计算方法[J]. 吉林大学学报:工学版,2021,51(2):472-477. |
| Ma Kai, Li Bang-hui, Yang Kun, et al. First and second⁃order sensitivity method of structure static displacement[J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(2):472-477. |
| [1] | 周焕林,郭鑫,王选,方立雪,龙凯. 考虑几何非线性的多相多孔结构拓扑优化设计[J]. 吉林大学学报(工学版), 2024, 54(10): 2754-2763. |
| [2] | 麻凯,李邦辉,杨坤,刘巧伶. 结构静态位移一阶和二阶灵敏度近似计算方法[J]. 吉林大学学报(工学版), 2021, 51(2): 472-477. |
| [3] | 周俊先,秦睿贤,陈秉智. 双面梯度多角薄壁结构的吸能特性[J]. 吉林大学学报(工学版), 2019, 49(5): 1584-1592. |
| [4] | 周晓勤,杨璐,张磊,陈立军. 具有负压缩性的铰接八面体结构的有限元分析[J]. 吉林大学学报(工学版), 2019, 49(3): 865-871. |
| [5] | 王小兵,陈建军,陈永琴,谢永强,陈龙 . 小区间参数不确定热机电耦合智能薄板的鲁棒控制[J]. 吉林大学学报(工学版), 2009, 39(01): 182-187. |
| [6] | 刘寒冰;张淼;魏健 . 结构动力响应分析的多重网格方法[J]. 吉林大学学报(工学版), 2008, 38(03): 619-0623. |
| [7] | 李成,刘治华,张平 . 具有初始位移的两层转子结构复合材料储能飞轮的应力及位移分析[J]. 吉林大学学报(工学版), 2007, 37(04): 828-832. |
| [8] | 王小兵,陈建军,高伟,赵俊,李金平. 层叠板结构瞬态温度场的灵敏度分析[J]. 吉林大学学报(工学版), 2006, 36(04): 456-461. |
| [9] | 刘寒冰, 刘文会, 张云龙, 赵 宏. 用弯矩曲率法分析预应力钢-混凝土组合梁的钢索受力状态[J]. 吉林大学学报(工学版), 2005, 35(02): 191-0194. |
| [10] | 刘昕晖, 宋玉泉, 陈塑寰. 电流变流体可变阻尼对系统振动的影响[J]. 吉林大学学报(工学版), 2004, (1): 20-24. |
| [11] | 宋学伟, 陈塑寰, 高峰, 杨志军. 车内噪声智能控制系统的模态最优控制[J]. 吉林大学学报(工学版), 2004, (1): 25-30. |
| [12] | 陈宇东. 亏损系统的特征值配置[J]. 吉林大学学报(工学版), 2001, (3): 36-40. |
| [13] | 郭学东, 谢军, 陈塑寰. 不确定性结构特征值上下界的估计方法[J]. 吉林大学学报(工学版), 2001, (1): 30-34. |
| [14] | 梁平, 张旭莉, 陈塑寰. 平面刚架结构支座变化公式[J]. 吉林大学学报(工学版), 2000, (2): 76-78. |
|
||