吉林大学学报(工学版) ›› 2024, Vol. 54 ›› Issue (10): 2754-2763.doi: 10.13229/j.cnki.jdxbgxb.20221624

• 车辆工程·机械工程 • 上一篇    

考虑几何非线性的多相多孔结构拓扑优化设计

周焕林1(),郭鑫1,王选1,2(),方立雪1,龙凯3   

  1. 1.合肥工业大学 土木与水利工程学院，合肥 230009
    2.天津大学 机械工程学院，天津 300072
    3.华北电力 大学 新能源电力系统国家重点实验室，北京 102206
  • 收稿日期:2022-12-25 出版日期:2024-10-01 发布日期:2024-11-22
  • 通讯作者: 王选 E-mail:zhouhl@hfut.edu.cn;xuanwang@hfut.edu.cn
  • 作者简介:周焕林（1973-），男，教授，博士. 研究方向：反问题与优化.E-mail： zhouhl@hfut.edu.cn
  • 基金资助:
    国家自然科学基金项目(12202129);中央高校科研业务费项目(JZ2022HGTB0291);中国博士后科学基金项目(2022M712358)

Topology optimization design of multiphase porous structures considering geometric nonlinearity

Huan-lin ZHOU1(),Xin GUO1,Xuan WANG1,2(),Li-xue FANG1,Kai LONG3   

  1. 1.College of Civil Engineering，Hefei University of Technology，Hefei 230009，China
    2.School of Mechanical Engineering，Tianjin University，Tianjin 300072，China
    3.State Key Laboratory for Alternate Electrical Power System with Renewable Energy Sources，North China Electric Power University，Beijing 102206，China
  • Received:2022-12-25 Online:2024-10-01 Published:2024-11-22
  • Contact: Xuan WANG E-mail:zhouhl@hfut.edu.cn;xuanwang@hfut.edu.cn

RICH HTML

 0   

PDF (PC)

46

摘要：

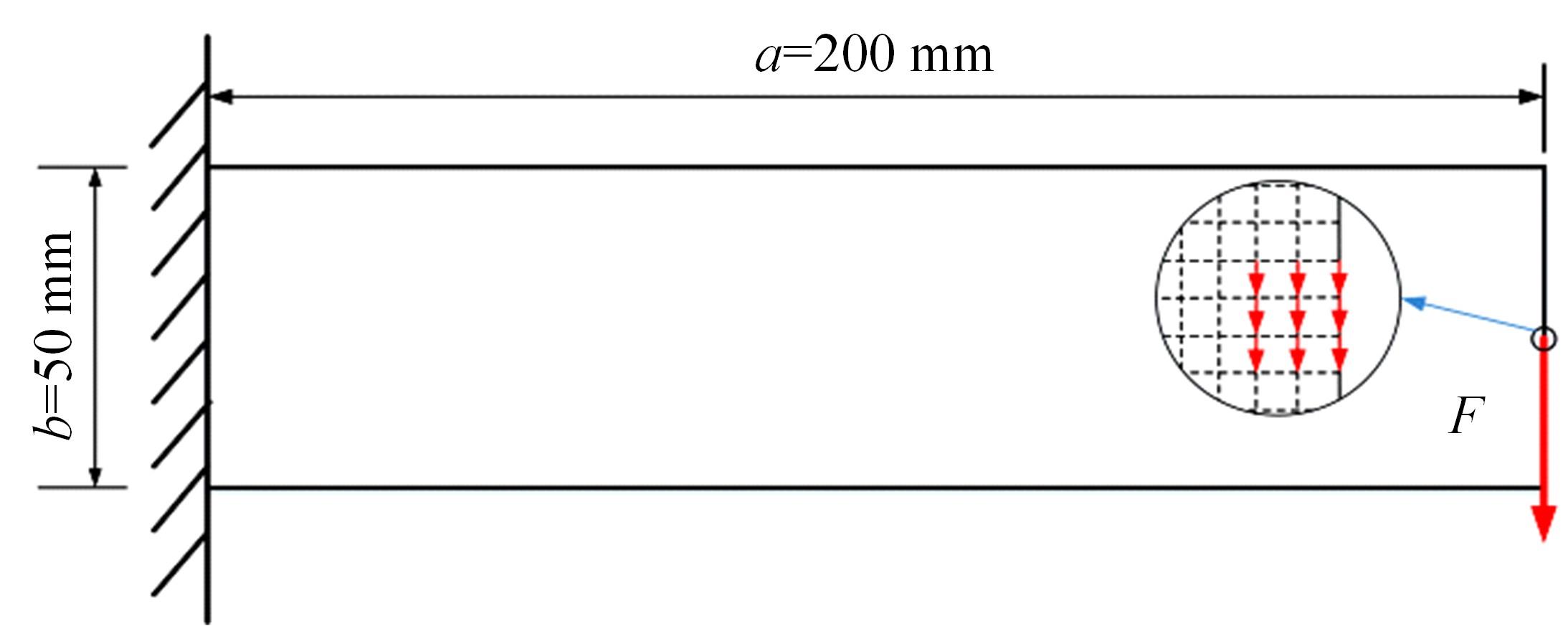
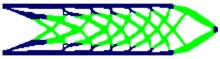
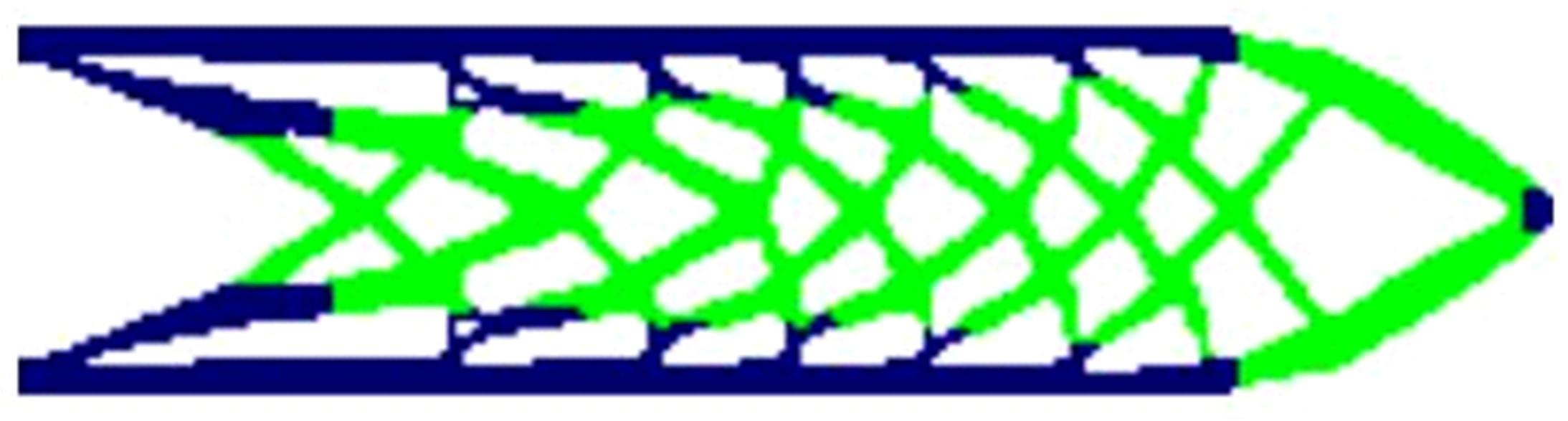
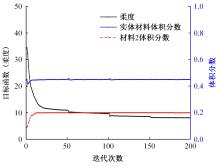
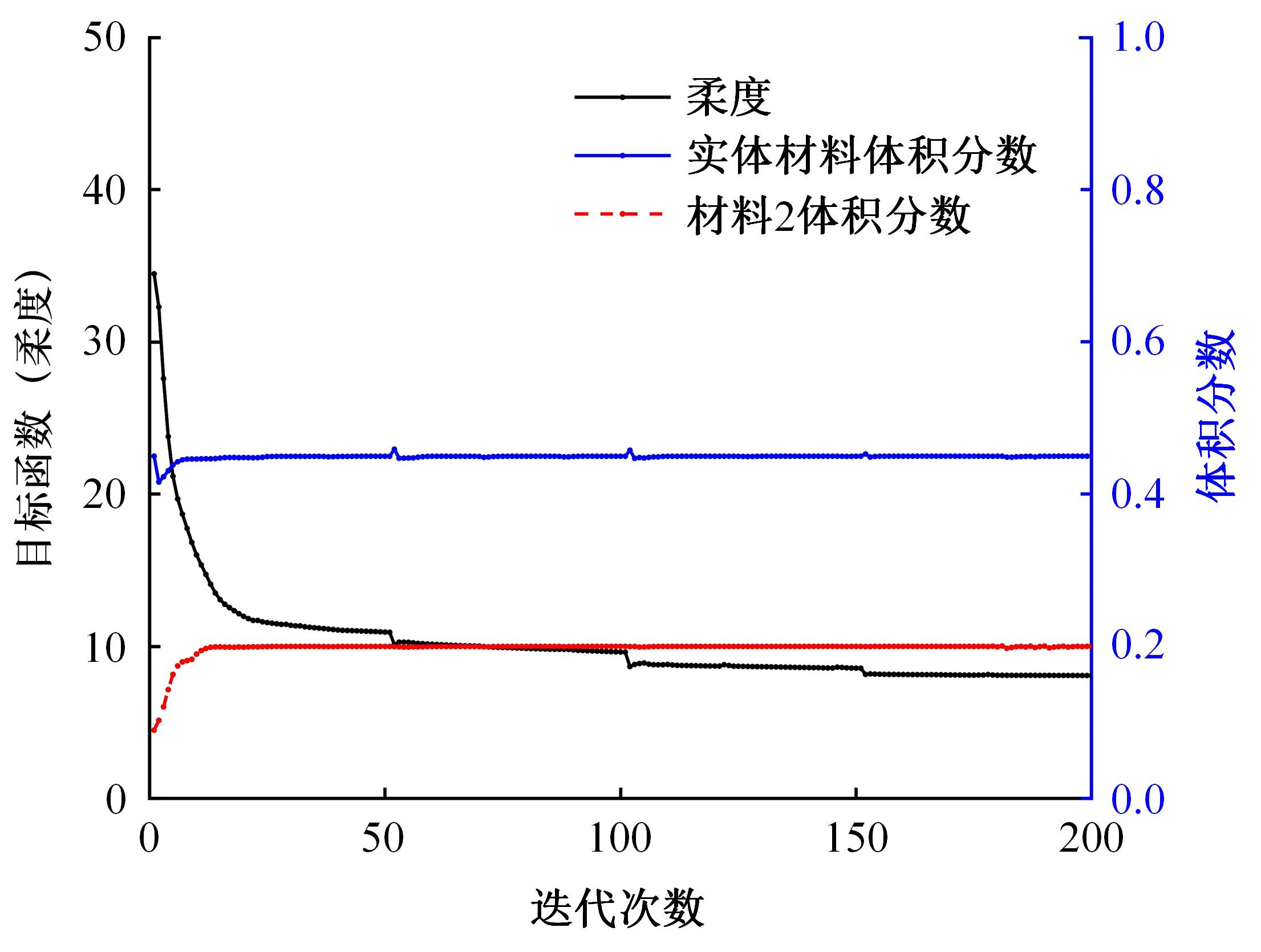
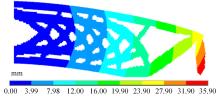
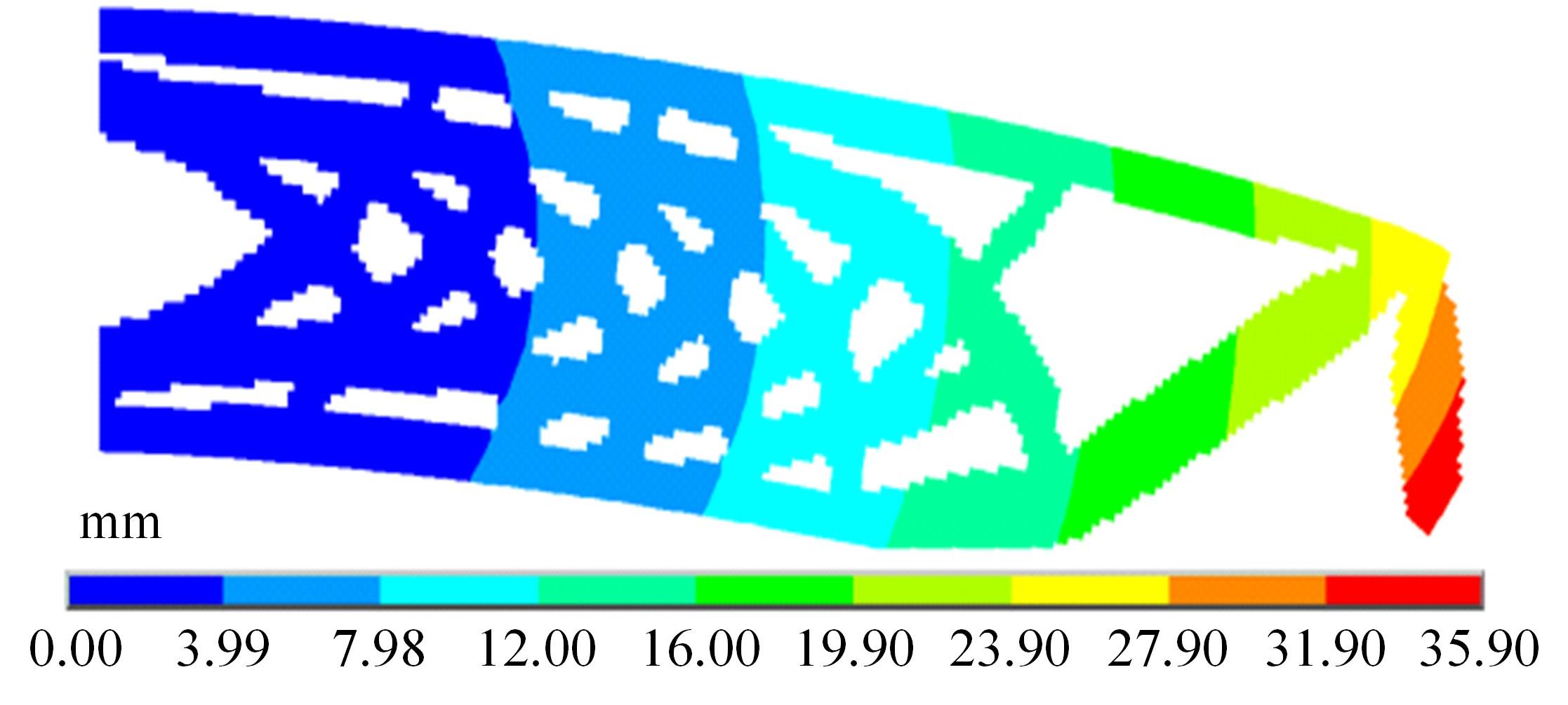
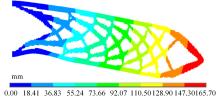
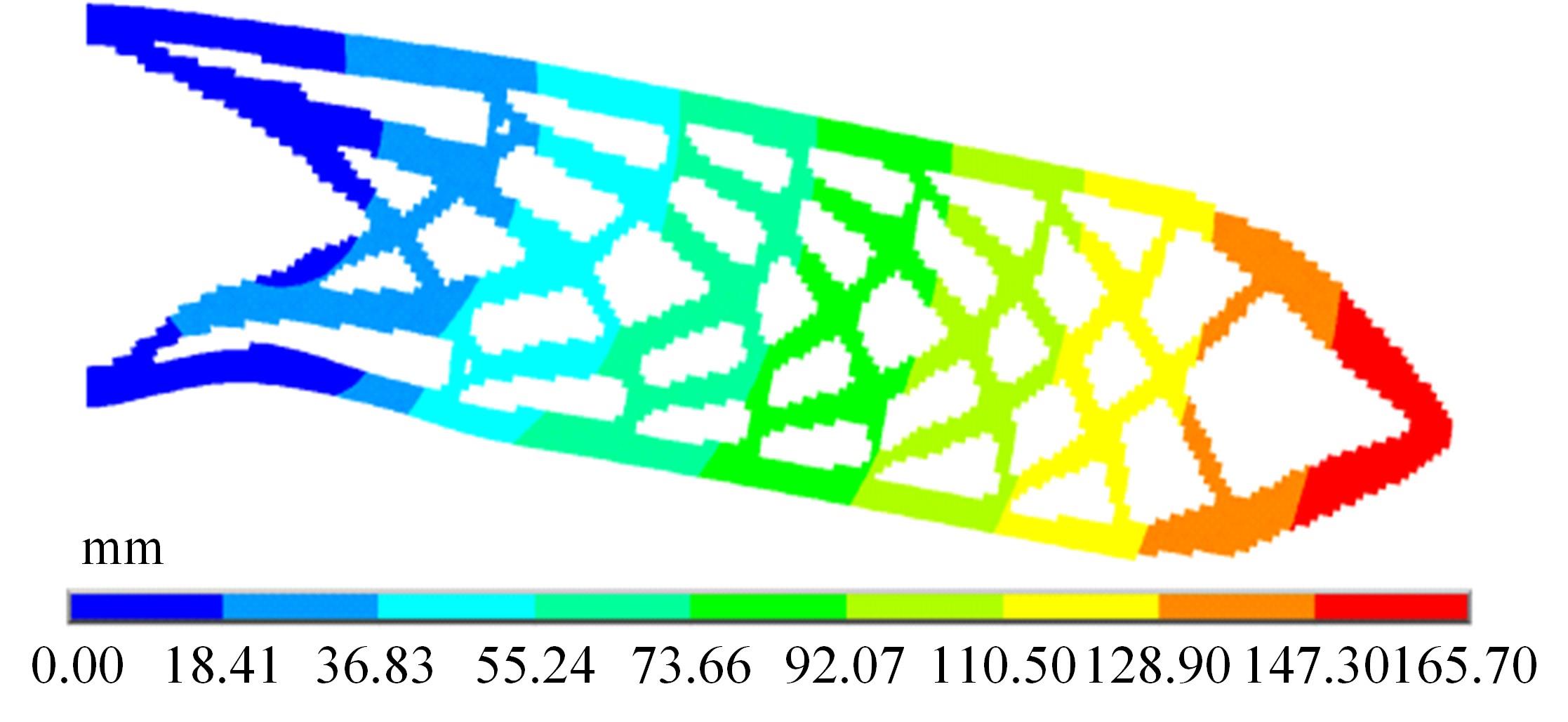
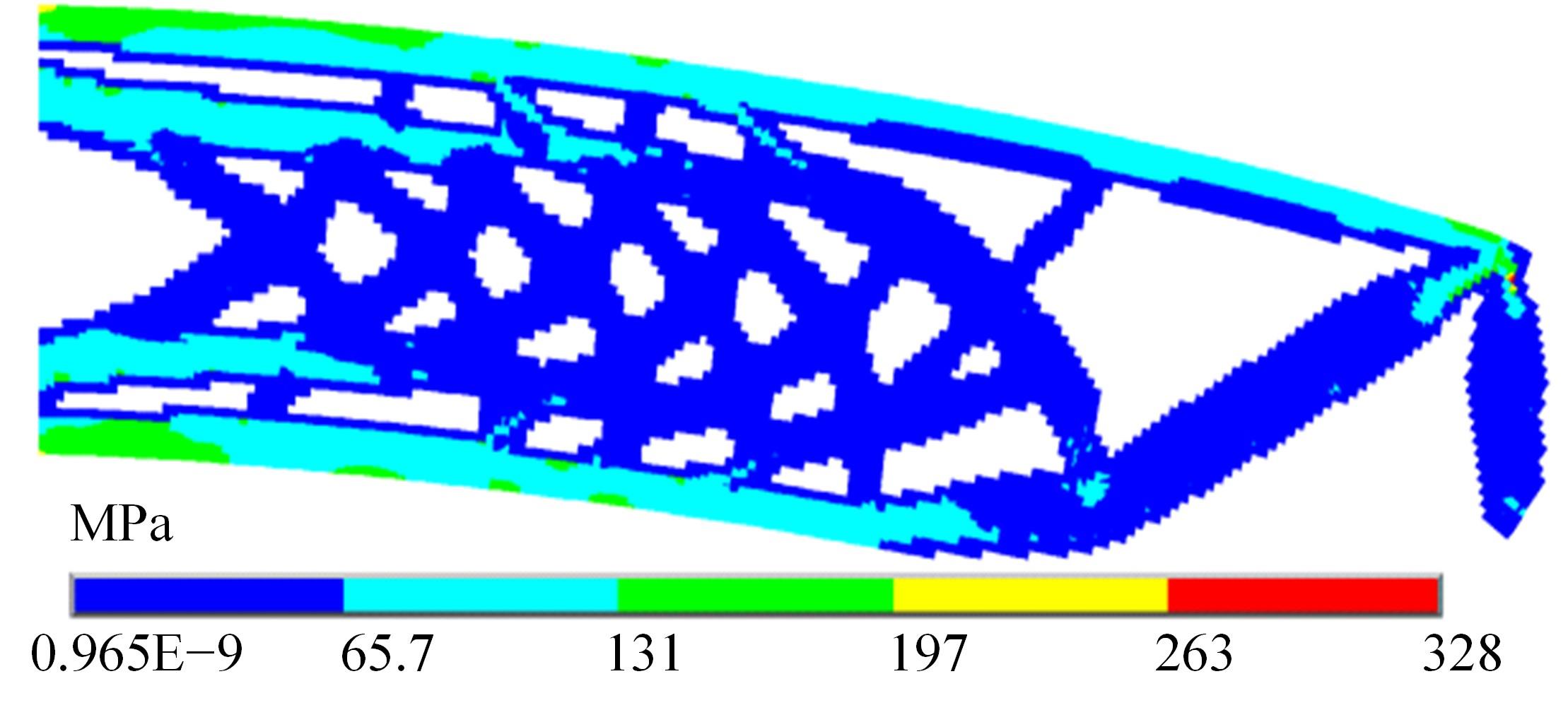
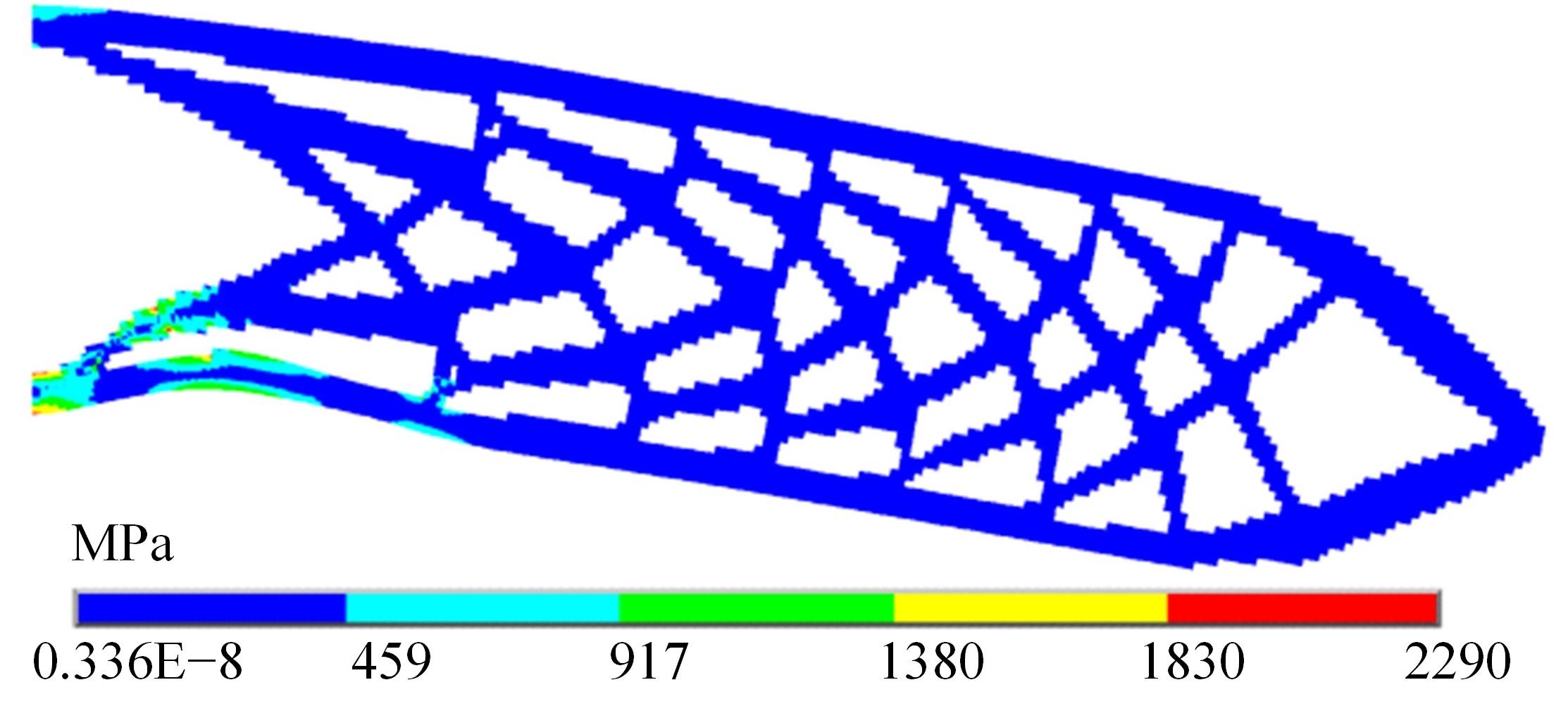
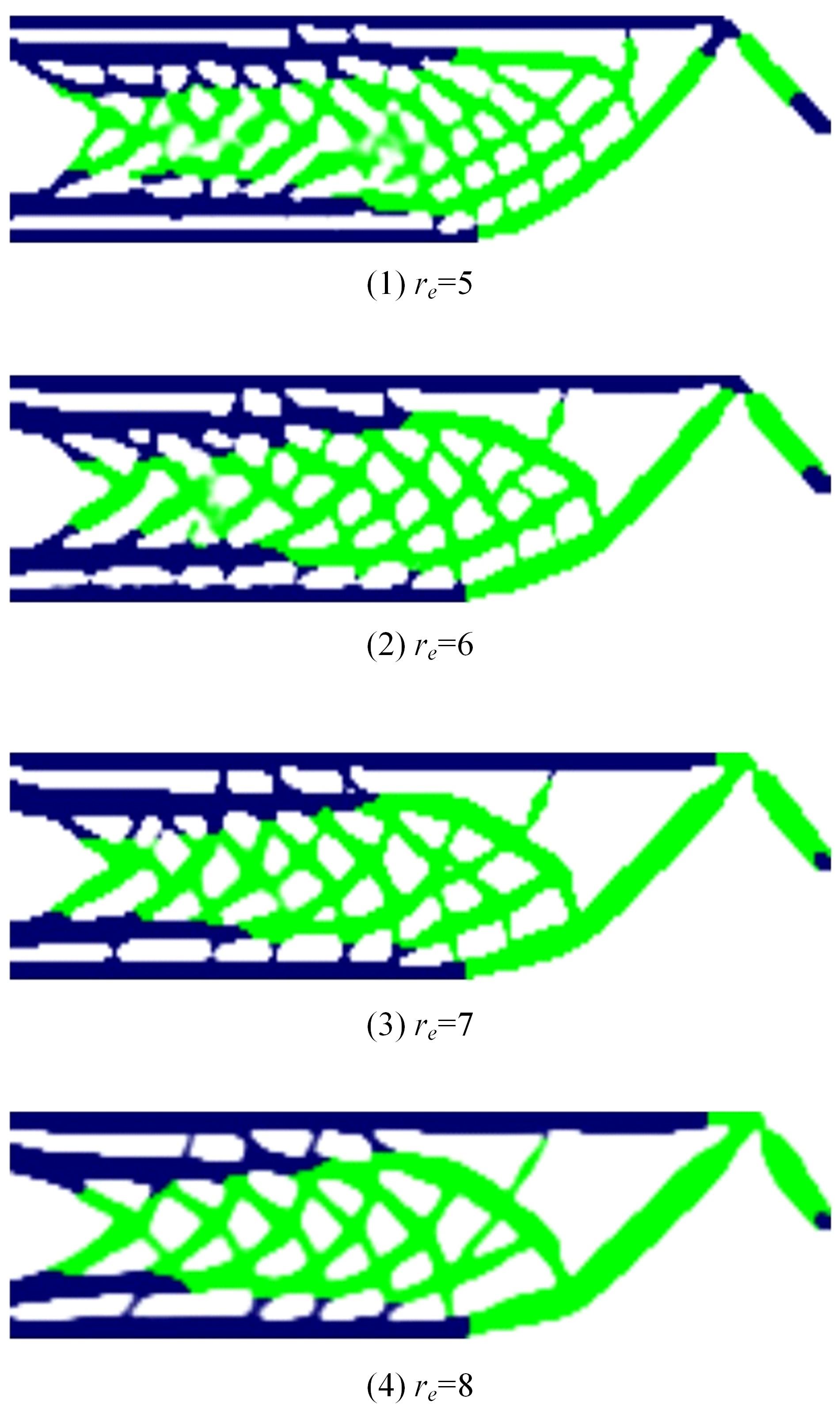
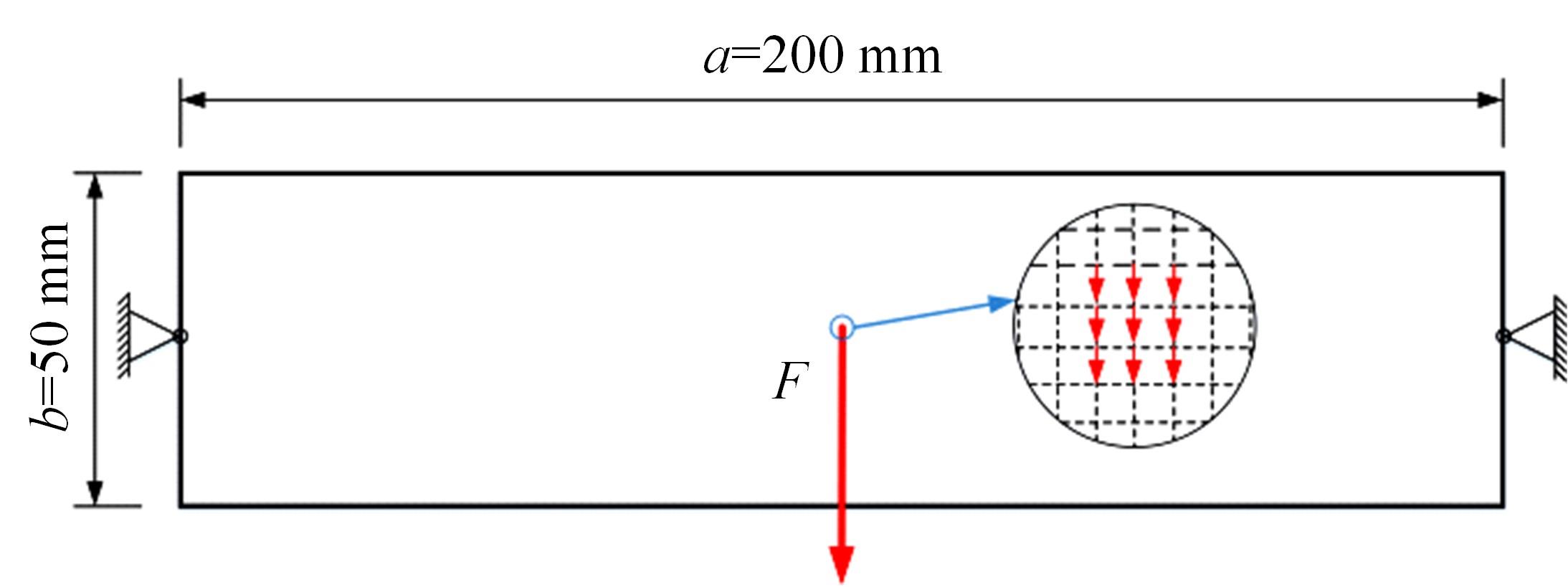
本文基于固体各向同性材料惩罚（solid lsotropic material with penalization，SIMP）插值模型提出一种考虑几何非线性效应的多相多孔结构拓扑优化设计方法。通过控制不同材料相的局部体积分数来形成多相多孔结构，利用p-范数将多个局部体积约束聚合为一个全局约束函数，以减少优化问题中的约束个数。采用附加超弹性技术避免几何大变形下的网格畸变问题。最后两个优化算例验证了本文方法的有效性，结果表明：本文方法可以实现不同材料相之间的合理分布，考虑几何非线性效应的多相多孔结构的位移、应力均更小。相比于单材料，考虑多相材料的多孔结构具有更好的性能。

关键词: 机械工程, 多孔结构, 几何非线性, 拓扑优化, 局部体积约束, 多相材料

Abstract:

A topology optimization method of multiphase porous structures considering geometric nonlinearity effects is proposed based on SIMP interpolation model. The multi-phase porous structure is formed by controlling the local volume fraction of different material phases. To reduce the number of constraints in the optimization problem， the p-norm is used to aggregate multiple local volume constraints into a global constraint function. The additional hyperelastic technique is used to avoid mesh distortion under large geometric deformation. Finally， two optimization examples are presented to verify the effectiveness of the proposed method. The optimization results show that the proposed method can achieve reasonable distribution among different material phases， and the displacement and stress of the porous structures considering the nonlinear effect are smaller. Compared with the single material structure， the porous structures composed of multi-materials has better mechanical properties.

Key words: mechanical engineering, porous structure, geometric nonlinearity, topology optimization, local volume constraint, multiphase materials

中图分类号: 

  • O342

图1

悬臂梁设计域"

图2

基于线弹性理论的两相材料多孔结构拓扑优化结果"

图3

考虑几何非线性的两相材料多孔结构拓扑优化果"

图4

考虑几何非线性的目标函数和体积分数的迭代史"

图5

非线性多孔结构的位移云图"

图6

线性多孔结构的位移云图"

图7

非线性多孔结构的应力云图"

图8

线性多孔结构的应力云图"

图9

不同局部体积过滤半径下的两相多孔结构拓扑优结果"

表1

不同局部体积过滤半径下的目标函数和体积分数值"

Casesre柔度实体体积分数材料2体积分数
Case 159.8320.4280.1993
Case 268.8420.4350.1973
Case 378.3570.4440.1986
Case 488.0860.4500.1999

图10

两点固定结构设计域"

图11

基于线弹性理论的两相材料多孔结构拓扑优化结果"

图12

考虑几何非线性的两相材料多孔结构拓扑优化果"

图13

基于线弹性理论的三相材料多孔结构拓扑优化果"

图14

考虑几何非线性的三相材料多孔结构拓扑优化果"

图15

考虑几何非线性的目标函数和体积分数的迭代史"

表2

不同材料相下的柔度值和最大位移值"

材料相数柔度实体体积分数最大位移/mm
单相1.0230.4004.100
两相0.8500.4003.405
三相0.7640.4003.055
1 Nazir A, Jeng J Y. Buckling behavior of additively manufactured cellular columns: experimental and simulation validation[J]. Materials & Design, 2020, 186: No.108349.
2 Clausen A, Aage N, Sigmund O. Exploiting additive manufacturing infill in topology optimization for improved buckling load[J]. Engineering, 2016, 2(2): 250-257.
3 Bai J, Zuo W. Hollow structural design in topology optimization via moving morphable component method[J]. Structural and Multidisciplinary Optimization, 2020, 61(1): 187-205.
4 Wu J, Niels A, Rudiger W, et al. Infill optimization for additive manufacturing-approaching bone-like porous structures[J]. IEEE Transactions on Visualization and Computer Graphics, 2017,4(2): 1127-1140.
5 Wu J, Clausen A, Sigmund O. Minimum compliance topology optimization of shell-infill composites for additive manufacturing[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 326: 358-375.
6 Liu C, Du Z, Zhang W, et al. Additive manufacturing-oriented design of graded lattice structures through explicit topology optimization[J]. Journal of Applied Mechanics, 2017, 84(8): No.081008.
7 Liu C, Du Z, Zhu Y, et al. Optimal design of shell-graded-infill structures by a hybrid MMC-MMV approach[J]. Computer Methods in Applied Mechanics and Engineering, 2020, 369: No. 113187.
8 Das S, Sutradhar A. Multi-phys ics topology optimization of functionally graded controllable porous structures: application to heat dissipating problems[J]. Materials & Design, 2020, 193: No.108775.
9 Hoang V N, Tran P, Nguyen N L, et al. Adaptive concurrent topology optimization of coated structures with nonperiodic infill for additive manufacturing[J]. Computer-Aided Design, 2020, 129: No.102918.
10 Hoang V N, Wang X, Nguyen-Xuan H. A three-dimensional multiscale approach to optimal design of porous structures using adaptive geometric components[J]. Composite Structures, 2021, 273: No.114296.
11 Dou S G. A projection approach for topology optimization of porous structures through implicit local volume control[J]. Structural and Multidisciplinary Optimization, 2020, 62(2): 835-850.
12 Long K, Chen Z, Zhang C W, et al. An aggregation-free local volume fraction formulation for topological design of porous structure[J]. Materials, 2021, 14(19): No.5726.
13 Zhao Z, Zhang X S. Design of graded porous bone-like structures via a multi-material topology optimization approach[J]. Structural and Multidisciplinary Optimization, 2021, 64(2): 677-698.
14 胡传丰, 任靖雯, 胡慧,等. 基于等几何分析的参数多孔结构拓扑优化[J]. 吉林大学学报:理学版, 2021, 59(1): 65-76.
Hu Chuan-feng, Ren Jing-wen, Hu Hui, et al. Topology optimization for parametric porous structure based on iso-geometric analysis[J]. Journal of Jilin University Science Edition, 2021, 59(1): 65-76.
15 Garaigordobil A, Ansola R, Querin O M, et al. Infill topology optimization of porous structures with discrete variables by the sequential element rejection and admission method[J]. Engineering Optimization, 2021, 55(3): 457-475.
16 Gan N, Wang Q. Topology optimization design of porous infill structure with thermo-mechanical buckling criteria[J]. International Journal of Mechanics and Materials in Design, 2022, 18(2): 267-288.
17 Huang J, Xu S, Ma Y, et al. A topology optimization method for hyperelastic porous structures subject to large deformation[J]. International Journal of Mechanics and Materials in Design, 2022, 18(2): 289-308.
18 Xue R, Liu C, Zhang W, et al. Explicit structural topology optimization under finite deformation via moving morphable void (MMV) approach[J]. Computer Methods in Applied Mechanics and Engineering, 2019, 344: 798-818.
19 文桂林, 刘杰, 陈梓杰, 等. 非线性连续体拓扑优化方法综述[J]. 力学学报, 2022, 54(10): 2659-2675.
Wen Gui-lin, Liu Jie, Chen Zi-jie, et al. A survey of nonlinear continuum topology optimization methods[J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(10): 2659-2675 .
20 陆念力,张宏生. 计及纵横变形效应的几何非线性三次样条梁单元[J]. 吉林大学学报:工学版, 2010, 40(3): 745-751.
Lu Nian-li, Zhang Hong-sheng. Geometric nonlinear cubic spline beam element with lateral and axial deformation effects[J]. Journal of Jilin University(Engineering and Technology Edition), 2010, 40(3): 745-751.
21 朱本亮, 张宪民, 李海, 等. 基于节点密度插值的多材料柔顺机构拓扑优化[J]. 机械工程学报, 2021, 57(15): 53-61.
Zhu Ben-liang, Zhang Xian-min, Li Hai, et al. Topology optimization of multi-material compliant mechanisms using node-density interpolation scheme[J]. Journal of Mechanical Engineering, 2021, 57(15): 53-61.
22 Zuo W, Saitou K. Multi-material topology optimization using ordered SIMP interpolation[J]. Structural and Multidisciplinary Optimization, 2017, 55(2): 477-491.
23 王选,胡平,龙凯.考虑嵌入移动孔洞的多相材料布局优化[J].力学学报,2019,51(3): 852-862.
Wang Xuan, Hu Ping, Long Kai. Multiphase material layout optimization considering embedding movable holes[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(3): 852-862.
24 Guo X, Zhang W, Zhong W. Stress-related topology optimization of continuum structures involving multi-phase materials[J]. Computer Methods in Applied Mechanics and Engineering, 2014, 268: 632-655.
25 Lazarov B S, Sigmund O. Filters in topology optimization based on Helmholtz‐type differential equations[J]. International Journal for Numerical Methods in Engineering, 2011, 86(6): 765-781.
26 Wang F, Lazarov B S, Sigmund O. On projection methods, convergence and robust formulations in topology optimization[J]. Structural and Multidisciplinary Optimization, 2011, 43(6): 767-784.
27 Luo Y J, Wang M Y, Kang Z. Topology optimization of geometrically nonlinear structures based on an additive hyperelasticity technique[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 286: 422-441.
28 Chen Q, Zhang X M, Zhu B L. A 213-line topology optimization code for geometrically nonlinear structures[J]. Structural and Multidisciplinary Optimization, 2019, 59(5): 1863-1879.
29 Buhl T, Pedersen C B W, Sigmund O. Stiffness design of geometrically nonlinear structures using topology optimization[J]. Structural and Multidisciplinary Optimization, 2000,19(2): 93-104.
30 Wang F, Lazarov B S, Sigmund O, et al. Interpolation scheme for fictitious domain techniques and topology optimization of finite strain elastic problems[J]. Computer Methods in Applied Mechanics and Engineering, 2014, 276: 453-472.
[1] 商蕾,杨萍,杨祥国,潘建欣,杨军,张梦如. 基于APSO-BP-PID控制的质子交换膜燃料电池热管理系统温度控制[J]. 吉林大学学报(工学版), 2024, 54(9): 2401-2413.
[2] 蒋林,李国龙,王时龙,徐凯,李喆裕. 基于主成分回归的进给轴热膨胀误差建模[J]. 吉林大学学报(工学版), 2024, 54(8): 2149-2155.
[3] 张则强,王灿,刘俊琦,计丹,刘思璐. 基于改进麻雀搜索算法的平行行排序问题[J]. 吉林大学学报(工学版), 2024, 54(7): 1851-1861.
[4] 回丽,金磊,宋万万,周松,安金岚. 转向架用SMA490BW钢不同焊接区域裂纹扩展速率[J]. 吉林大学学报(工学版), 2024, 54(3): 650-656.
[5] 杨志军,张驰,黄观新. 基于浮动坐标法的刚柔耦合定位平台力学模型[J]. 吉林大学学报(工学版), 2024, 54(2): 385-393.
[6] 石林榕,赵武云. 西北寒旱农区胡麻滚勺式精量穴播器的设计及试验[J]. 吉林大学学报(工学版), 2023, 53(9): 2706-2717.
[7] 柴博森,王广义,闫东,朱国仁,张进,吕恒升. 液力变矩器空化数值模拟及对性能的影响[J]. 吉林大学学报(工学版), 2023, 53(8): 2236-2244.
[8] 陈国辉,徐业银,焦映厚. 考虑偏转的斜齿轮啮合刚度及其振动分析[J]. 吉林大学学报(工学版), 2023, 53(7): 1902-1910.
[9] 陈贵升,罗国焱,李靓雪,黄震,李一. 柴油机颗粒捕集器孔道流场及其高原环境下噪声特性分析[J]. 吉林大学学报(工学版), 2023, 53(7): 1892-1901.
[10] 王峰,刘双瑞,王佳盈,宋佳玲,王俊,张久鹏,黄晓明. 尺寸和形状效应对多孔结构风阻系数的影响[J]. 吉林大学学报(工学版), 2023, 53(6): 1677-1685.
[11] 李胜,朱佳,黄德惠,陈存福,费洪庆,丰伟,胡兴军. 空冷中冷器百叶窗翅片结构参数优化[J]. 吉林大学学报(工学版), 2023, 53(4): 998-1006.
[12] 王建,于威,王斌. 高原状态下甲醇替代率对柴油机燃烧与排放的影响[J]. 吉林大学学报(工学版), 2023, 53(4): 954-963.
[13] 于立娟,安阳,何佳龙,李国发,王升旭. 机电装备载荷谱外推技术研究进展及发展趋势[J]. 吉林大学学报(工学版), 2023, 53(4): 941-953.
[14] 柴博森,闫东,王广义,左文杰. 制动工况桃腔偶合器三维涡特征分析及仿真评价[J]. 吉林大学学报(工学版), 2023, 53(11): 3045-3055.
[15] 孙舒杨,程玮斌,张浩桢,邓向萍,齐红. 基于深度学习的两阶段实时显式拓扑优化方法[J]. 吉林大学学报(工学版), 2023, 53(10): 2942-2951.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
版权所有 © 《吉林大学学报(工学版)》编辑部
地址：长春市人民大街5988号　电话：+86-431-85095297　传真：+86-431-85094074　E-mail: xbgxb@jlu.edu.cn
本系统由北京玛格泰克科技发展有限公司设计开发