基于卡尔曼滤波预测策略的动态多目标优化算法

doi:10.13229/j.cnki.jdxbgxb20210082

摘要/Abstract

摘要：

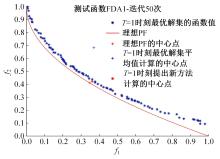
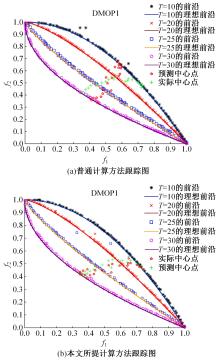
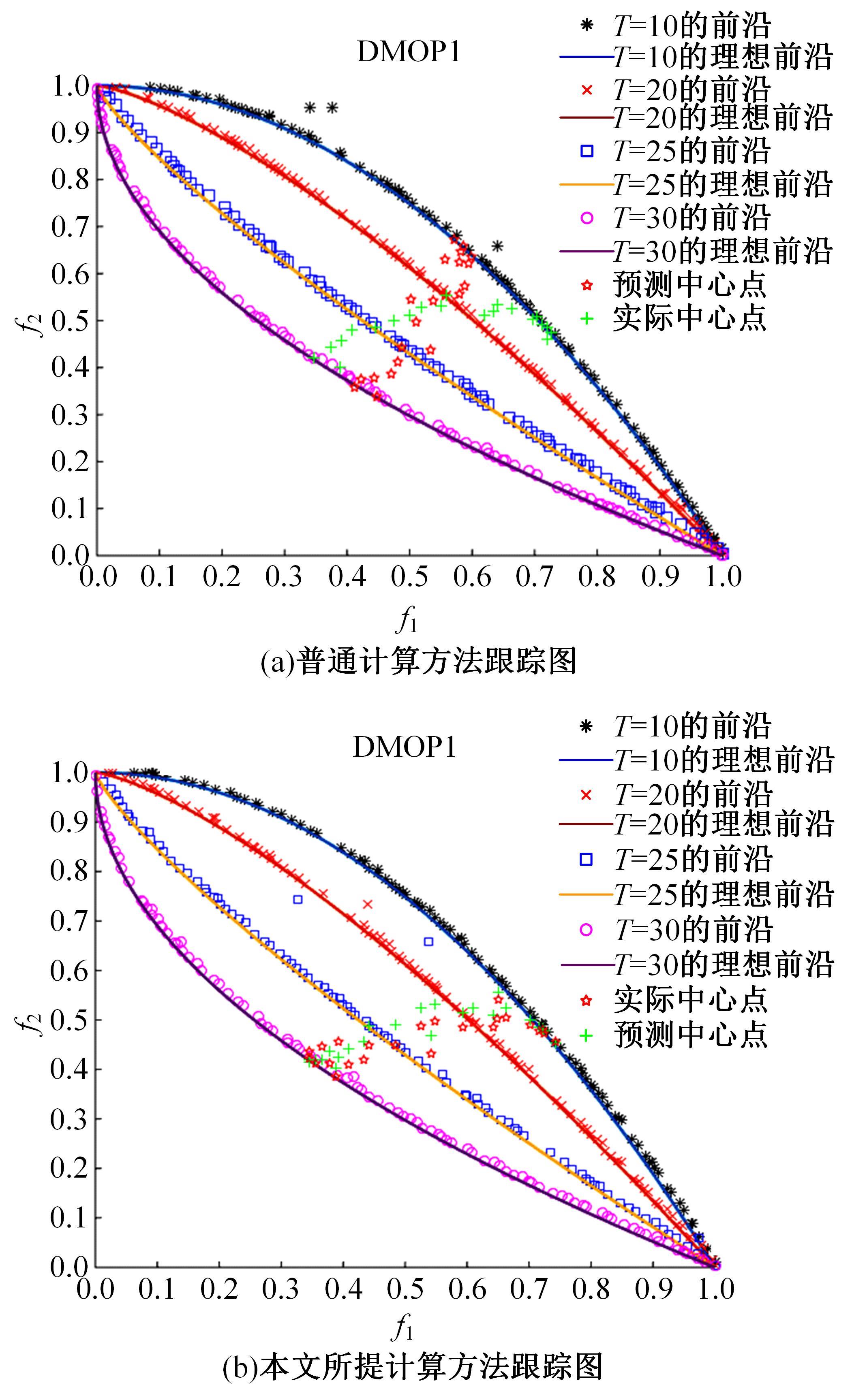
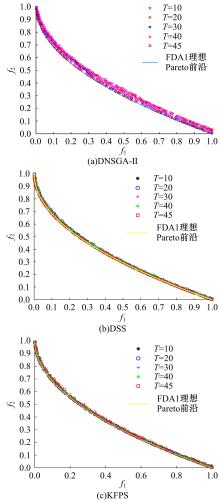
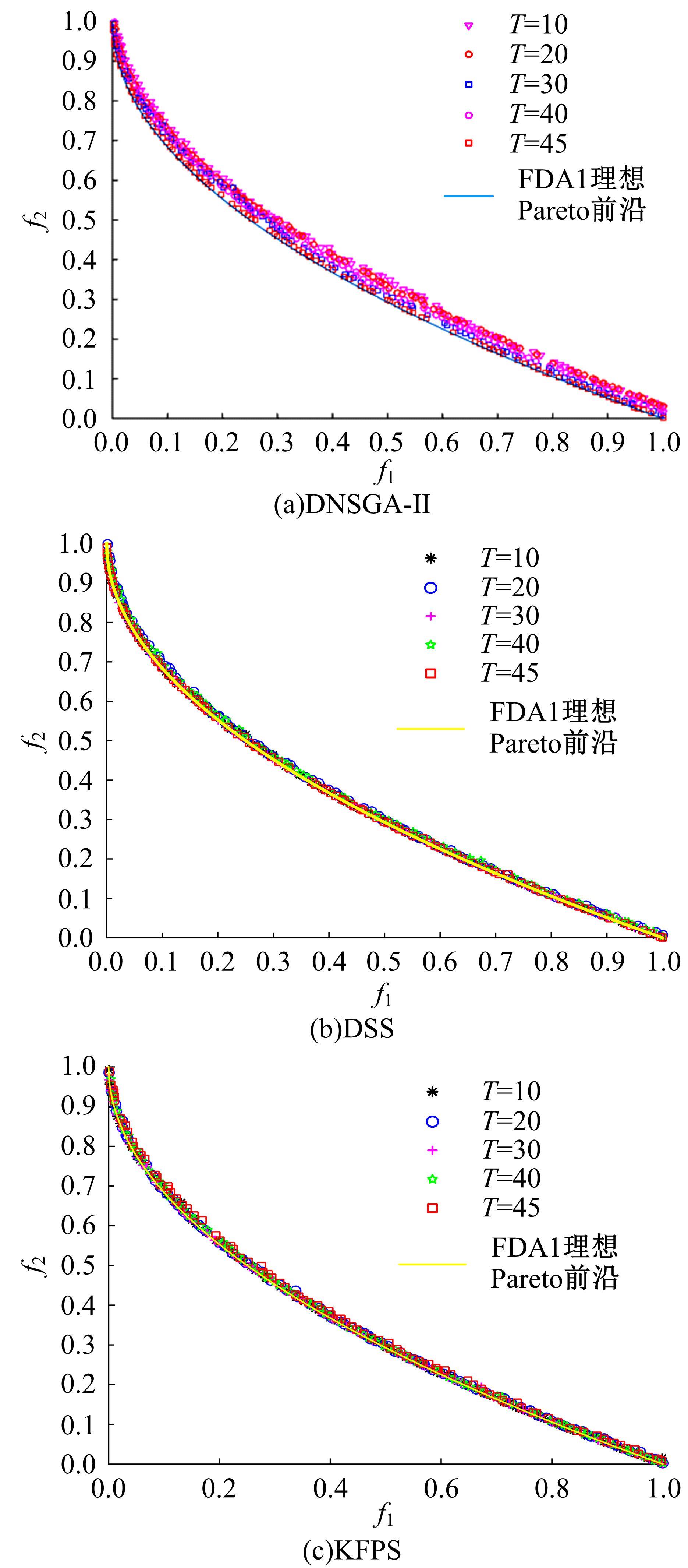
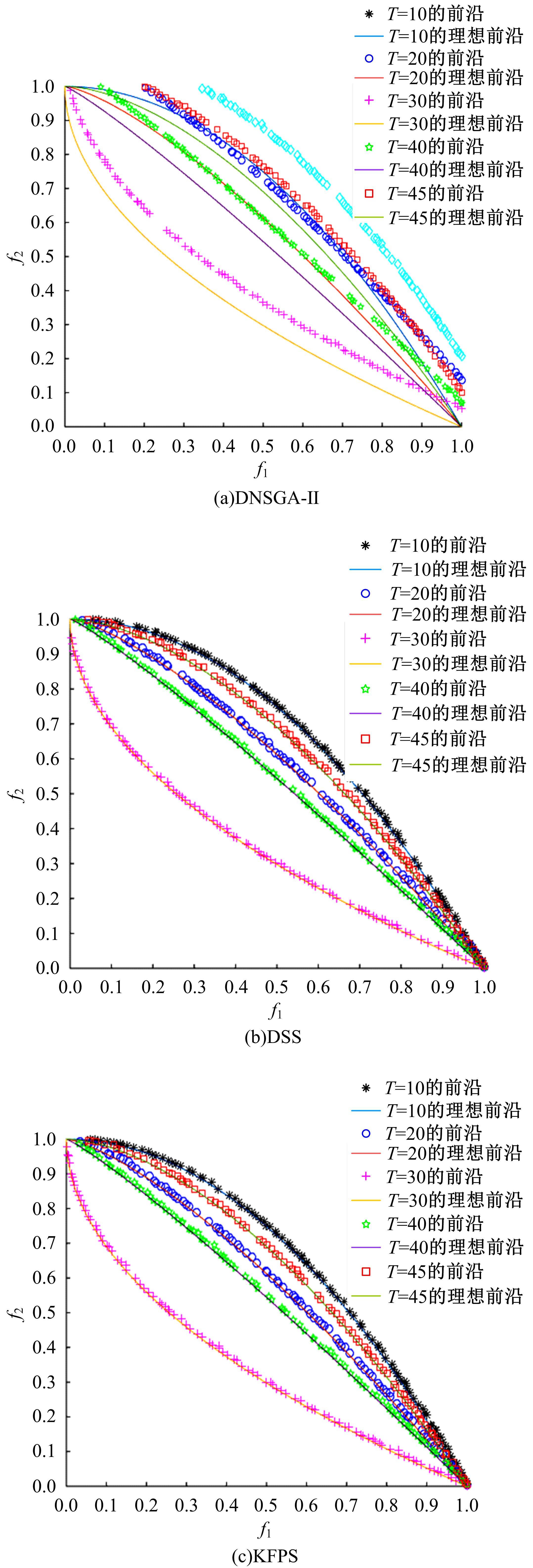
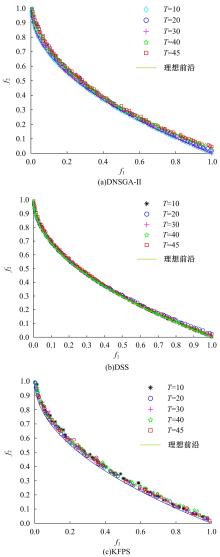
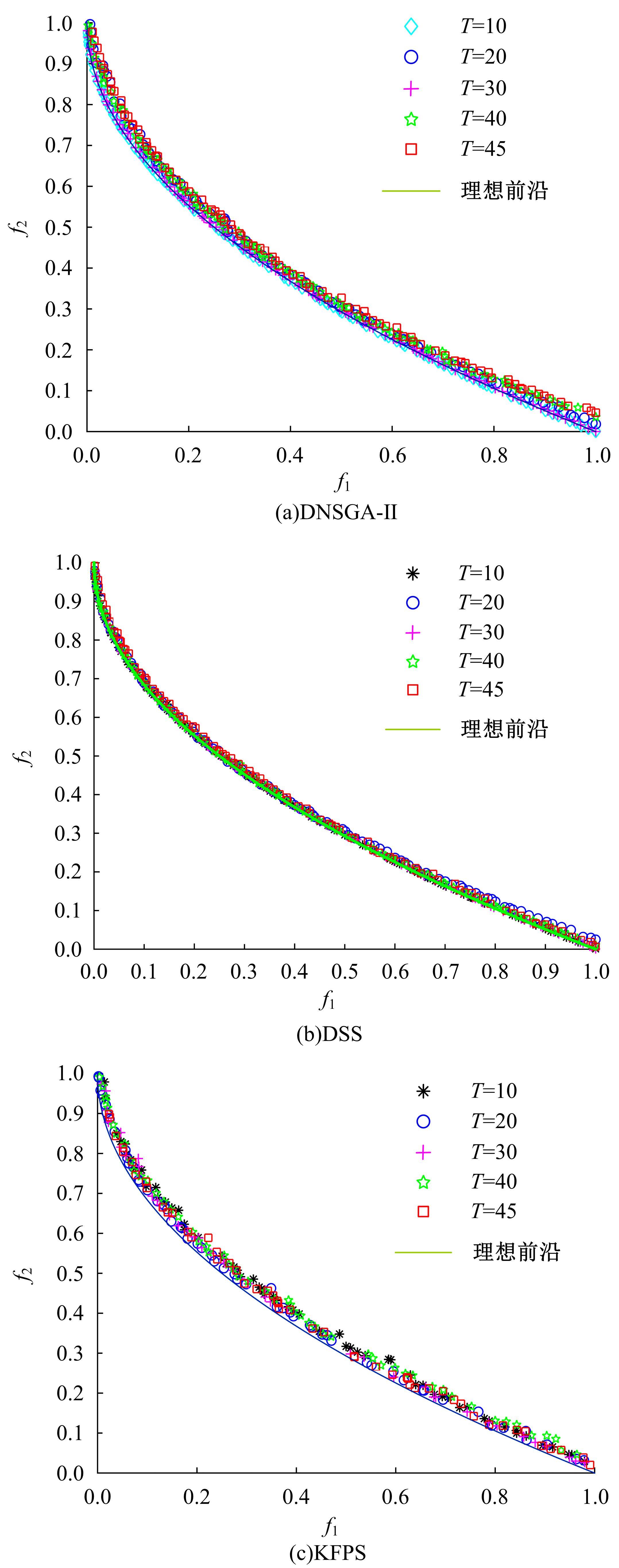
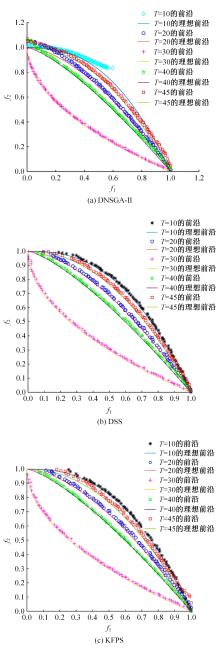
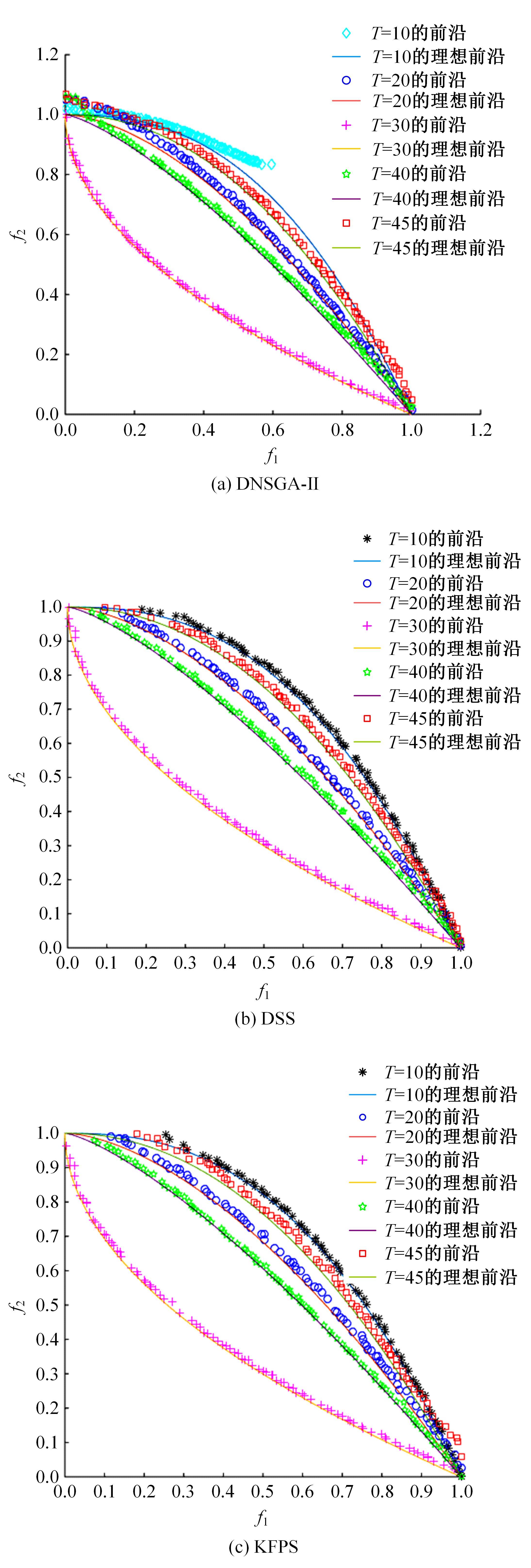
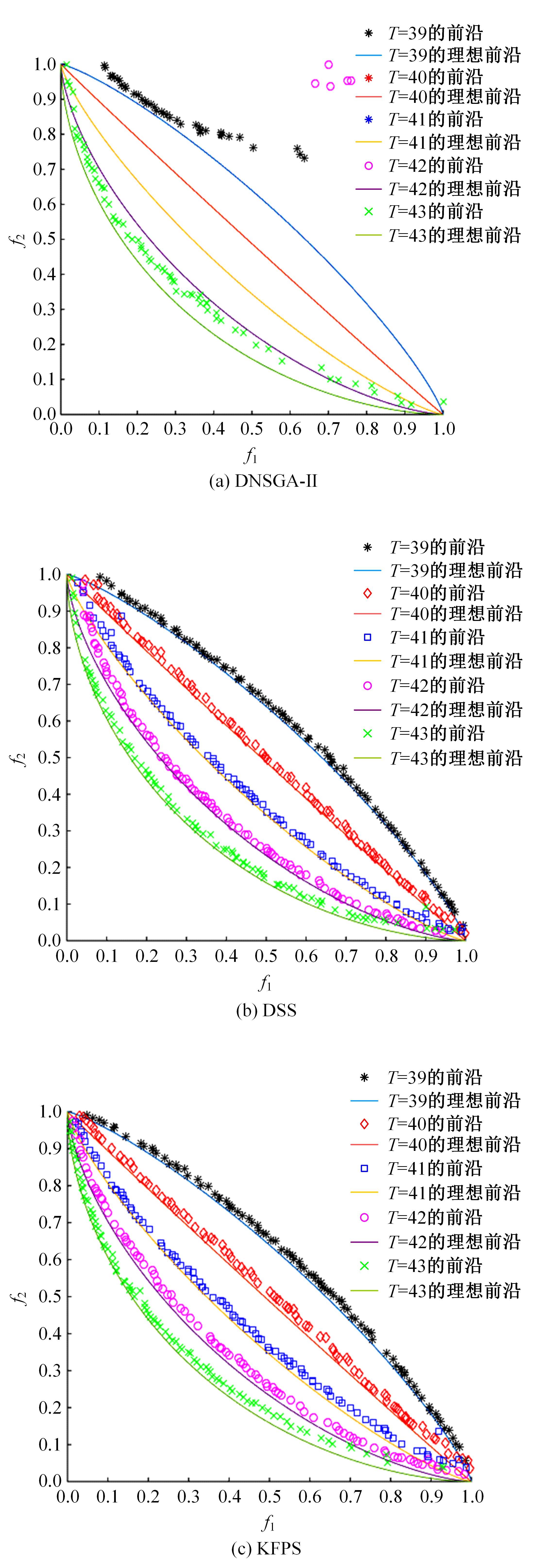
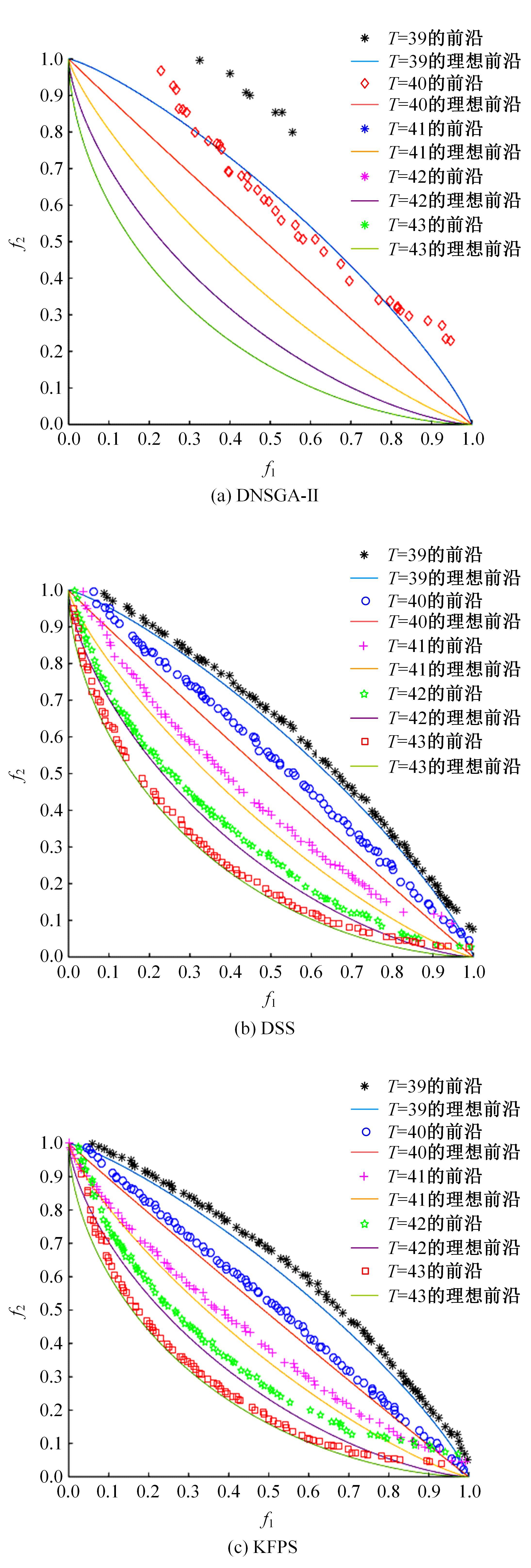
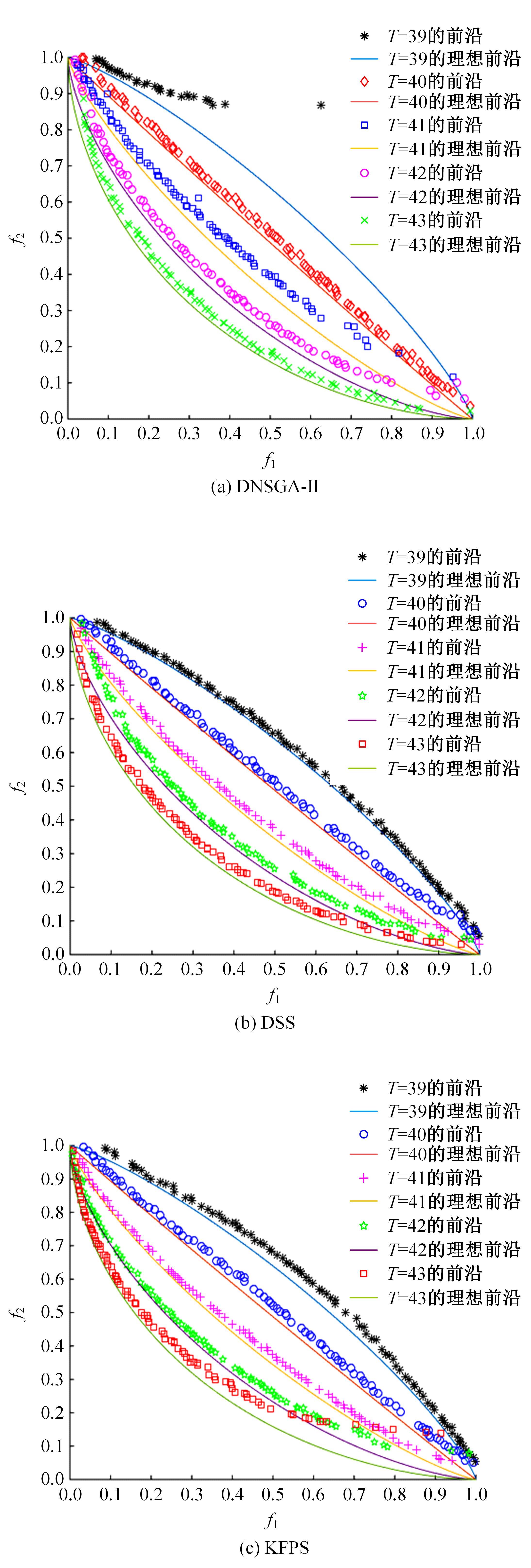
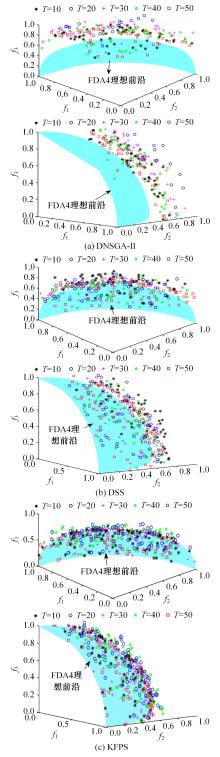
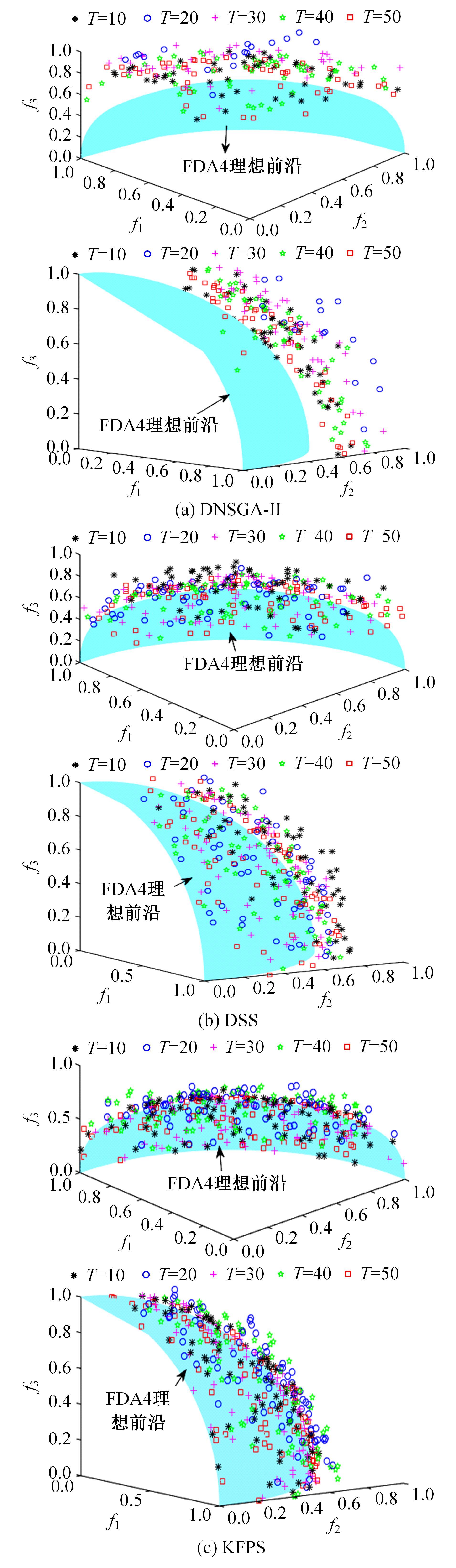
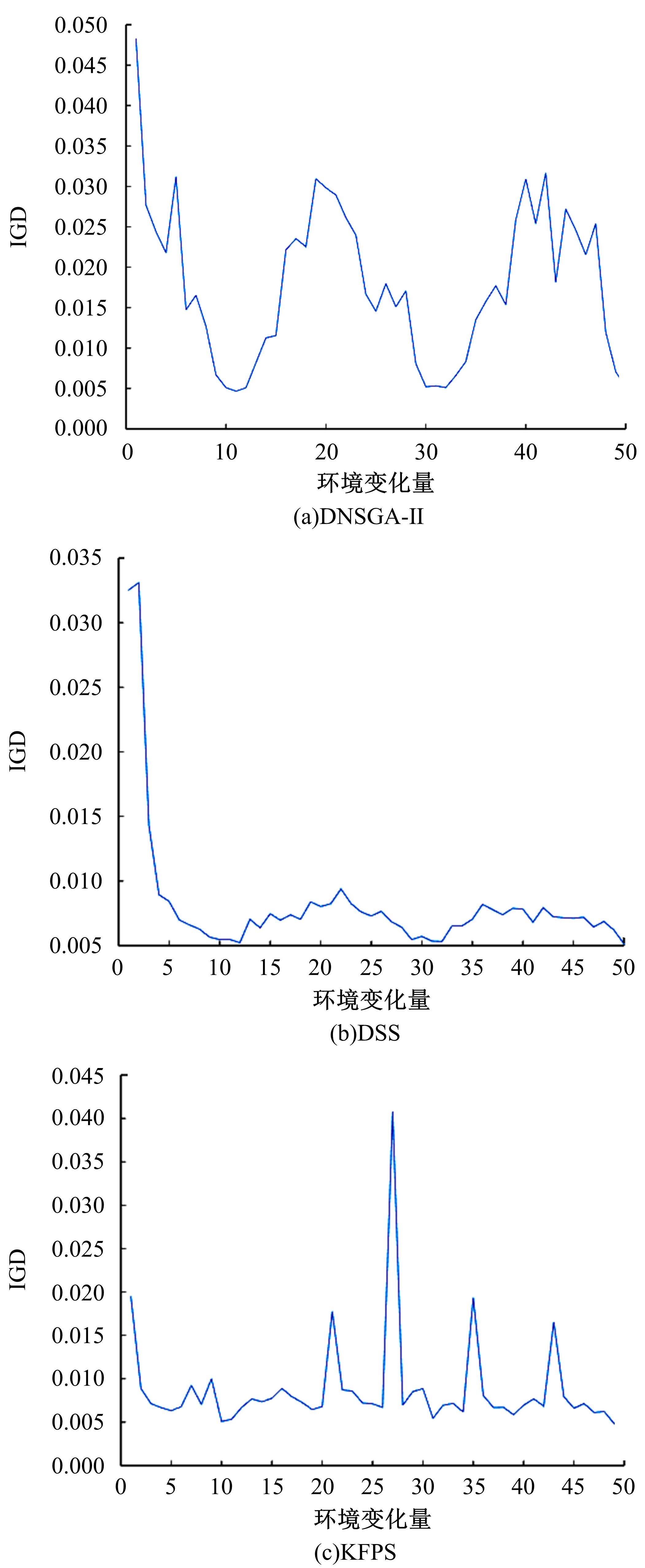
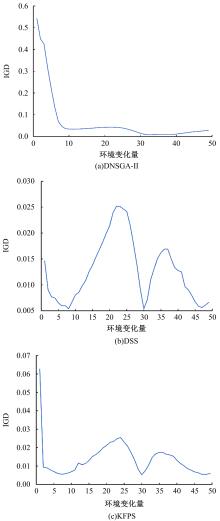
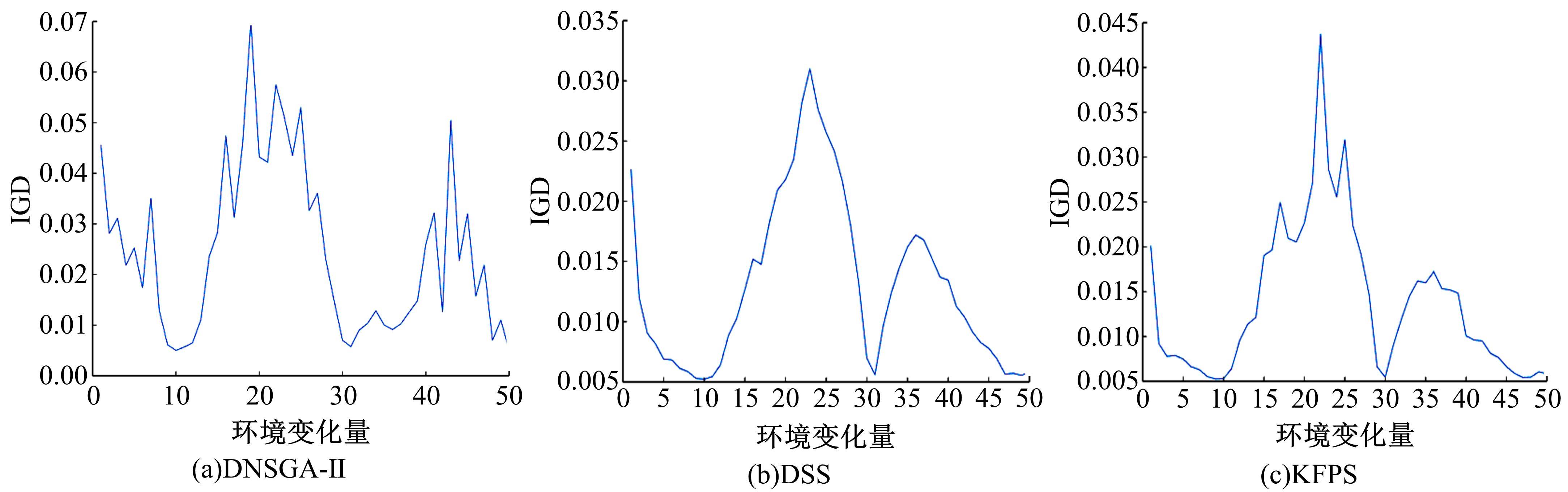
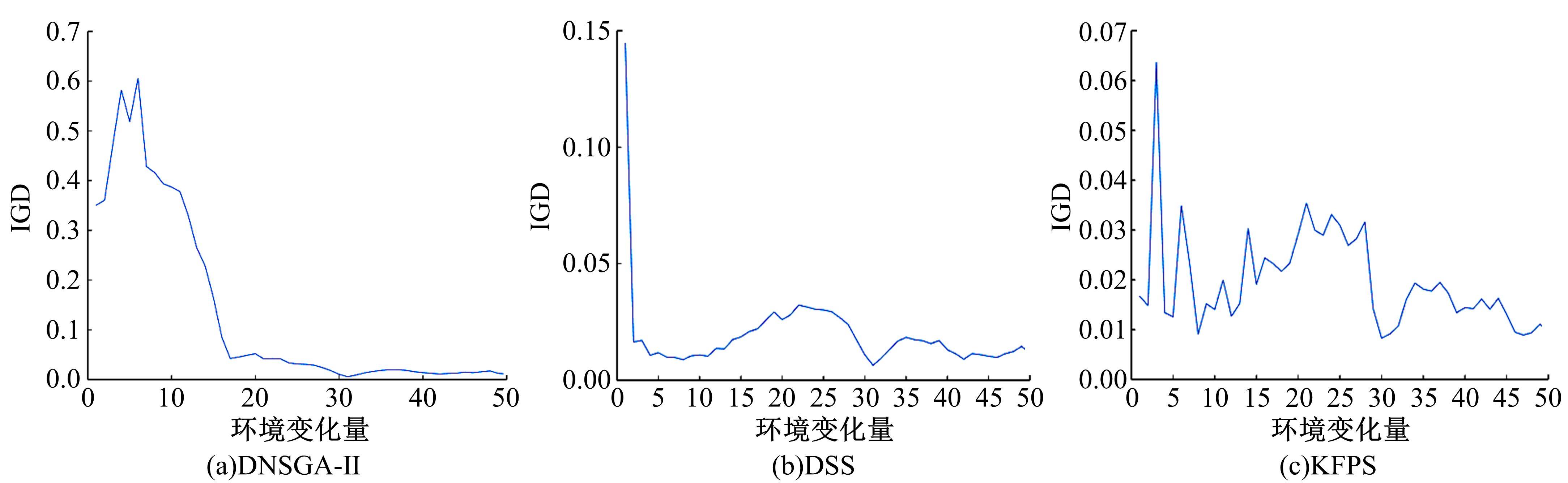
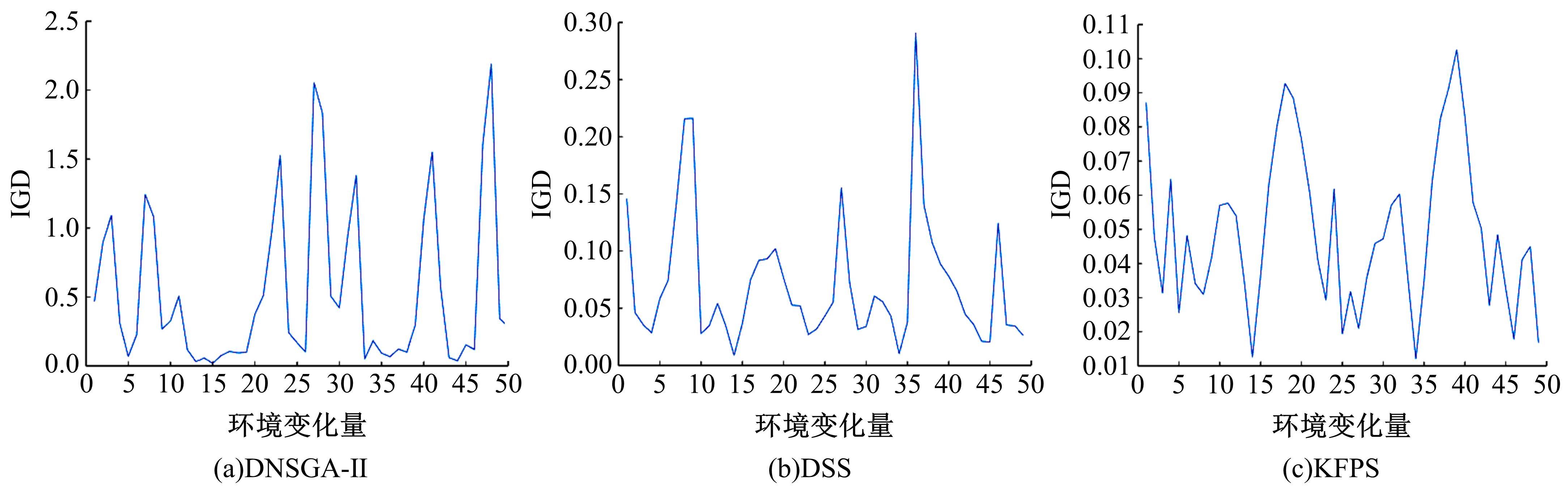
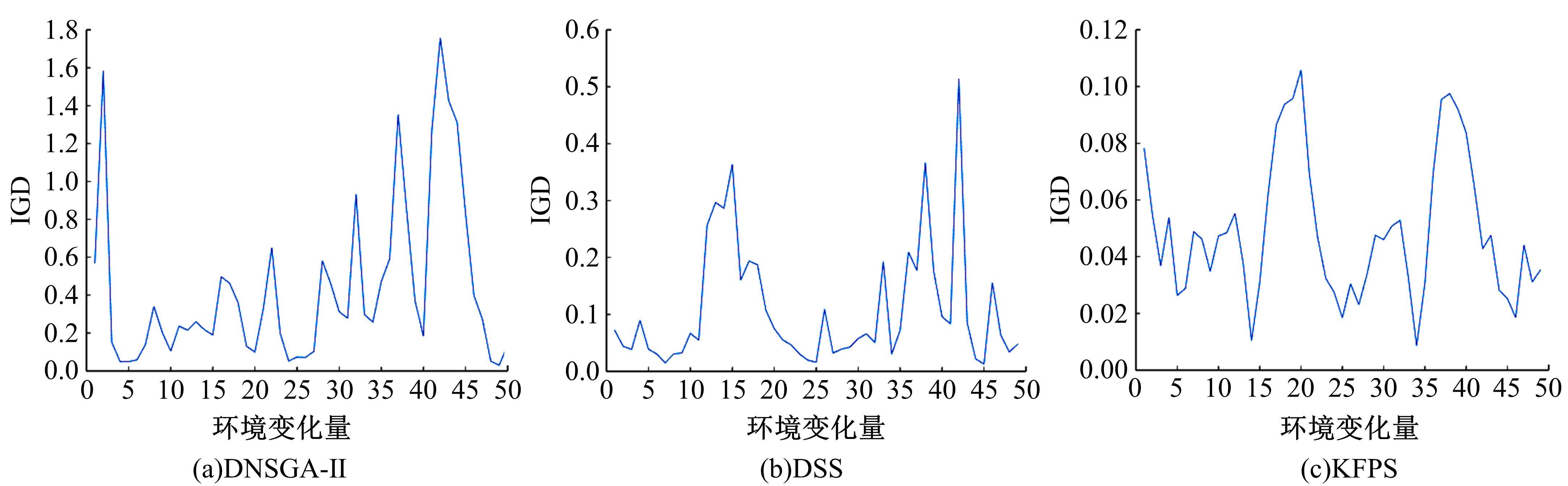
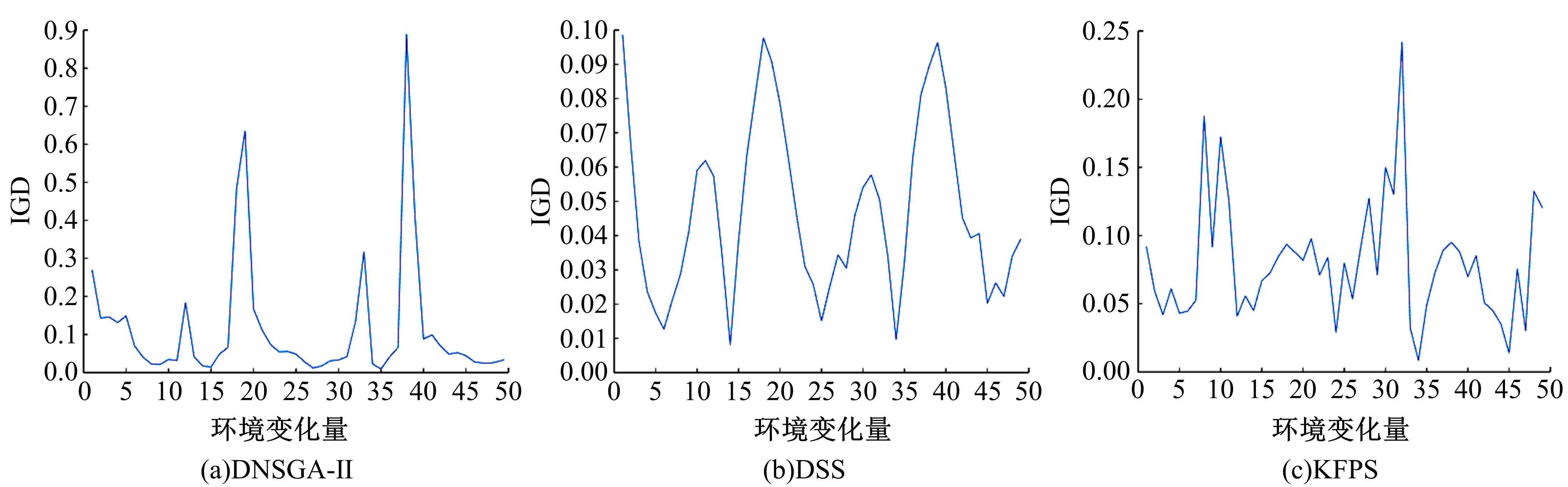
为利用种群历史信息更有效地处理动态多目标优化的环境变化问题，提出了一种基于卡尔曼滤波预测并修正种群中心点位置的动态多目标优化算法。当环境变化后，利用卡尔曼滤波预测模型结合上一时刻的中心点预测当前时刻的种群中心点，使用近似理想Pareto最优解集中心点对该预测值进行误差修正，并基于修正后的中心点生成新的个体以重新初始化种群。为增加种群多样性，在算法运行期间从搜索空间随机生成5个新的个体，并随机替换当前种群中相应数量的个体。将本文算法与其他动态多目标优化算法在多个测试函数中进行了对比实验，结果表明，本文算法在整个进化过程中，改进的逆世代距离（MIGD）值都相对比较小，逆世代距离（IGD）值总体上比对比算法小，计算耗时与对比算法相当。

关键词: 模式识别与智能系统, 动态多目标优化, 进化算法, 卡尔曼滤波预测

Abstract:

In order to deal with the environmental changes of dynamic multi-objective optimization more effectively， a dynamic multi-objective optimization algorithm based on Kalman filter prediction strategy is proposed. In the evolution process， a new calculation method is used to calculate the population center point. When the environment changes， the Kalman filter prediction model is used to predict the current population center point， and the approximate true Pareto center point of optimal solution set is used to correct the prediction value， and new individuals are generated based on the modified center point to reinitialize the population during the running of the algorithm； In order to increase the diversity of the population， five new individuals are randomly generated from the search space during the operation of the algorithm， and the corresponding number of individuals in the current population are randomly replaced. Compared with other dynamic multi-objective optimization algorithms in multiple test functions， the results show that the value of Modified Inverted Generational Distance （MIGD） in the whole evolution process is relatively small， and the value of Inverted Generational Distance （IGD） in the evolution is generally smaller than that of the contrast algorithm， and the calculation time is equivalent to that of the comparison algorithm.

Key words: pattern recognition and intelligent system, dynamic multi-objective optimization, evolutionary algorithm, Kalman filter prediction

中图分类号:

TP273

马永杰,陈敏. 基于卡尔曼滤波预测策略的动态多目标优化算法[J]. 吉林大学学报(工学版), 2022, 52(6): 1442-1458.

Yong-jie MA,Min CHEN. Dynamic multi⁃objective optimization algorithm based on Kalman filter prediction strategy[J]. Journal of Jilin University(Engineering and Technology Edition), 2022, 52(6): 1442-1458.

图/表 23

图 1

图2

表1

表2

表3

图3

图4

图5

图6

图7

图8

图9

图10

图11

图12

图13

图14

图15

图16

图17

图18

图19

表4

参考文献 29

1	孙宝凤, 任欣欣, 郑再思, 等. 考虑工人负荷的多目标流水车间优化调度[J]. 吉林大学学报: 工学版, 2021, 51(3): 900-909.
	Sun Bao-feng, Ren Xin-xin, Zheng Zai-si, et al. Multi⁃objective flow shop optimal scheduling considering worker's load[J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(3): 900-909.
2	Marichelvam M K, Prabaharan T, Yang X S. A discrete firefly algorithm for the multi-objective hybrid flowshop scheduling problems[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(2): 301-305.
3	马永杰, 陈敏, 龚影, 等. 动态多目标优化进化算法研究进展[J]. 自动化学报, 2020, 46(11): 2302-2318.
	Ma Yong-jie, Chen Min, Gong Ying, et al. Research progress of dynamic multi-objective optimization evolutionary algorithm[J]. Acta Automatica Sinica, 2020, 46(11): 2302-2318.
4	刘敏, 曾文华. 记忆增强的动态多目标分解进化算法[J]. 软件学报, 2013, 24(7): 1571-1588.
	Liu Min, Zeng Wen-hua. Memory enhanced dynamic multi-objective evolutionary algorithm based on decomposition[J]. Journal of Software, 2013, 24(7): 1571-1588.
5	Kordestani J K, Ranginkaman A E, Meybodi M R, et al. A novel framework for improving multi-population algorithms for dynamic optimization problems: a scheduling approach[J]. Swarm and Evolutionary Computation, 2019, 44: 788-805.
6	Woldesenbet Y G, Yen G G. Dynamic evolutionary algorithm with variable relocation[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(3): 500-513.
7	胡成玉, 姚宏, 颜雪松. 基于多粒子群协同的动态多目标优化算法及应用[J]. 计算机研究与发展, 2013, 50(6): 1313-1323.
	Hu Cheng-yu, Yao Hong, Yan Xue-song. Multiple particle swarms coevolutionary algorithm for dynamic multi-objective optimization problems and its application[J]. Journal of Computer Research and Development, 2013, 50(6): 1313-1323.
8	Zhou A M, Jin Y C, Zhang Q F. A population prediction strategy for evolutionary dynamic multiobjective optimization[J]. IEEE Transactions on Cybernetics, 2014, 44(1): 40-53.
9	Wang C, Yen G G, Jiang M. A grey prediction-based evolutionary algorithm for dynamic multiobjective optimization[J]. Swarm and Evolutionary Computation, 2020, 56: No. 100695.
10	Zou F, Yen G G, Tang L X. A knee-guided prediction approach for dynamic multi-objective optimization[J]. Information Sciences, 2020,509: 193-209.
11	Hatzakis I, Wallace D. Dynamic multi-objective optimization with evolutionary algorithms: a forward-looking approach[C]∥Proceedings of the 8th annual conference on Genetic and evolutionary computation. Seattle, Washington, USA, 2006: 1201-1208.
12	Koo W T, Goh C K, Tan K C. A predictive gradient strategy for multiobjective evolutionary algorithms in a fast changing environment[J]. Memetic Computing, 2010, 2(2): 87-110.
13	Ahrari A, Elsayed S, Sarker R, et al. Weighted pointwise prediction method for dynamic multiobjective optimization[J]. Information Sciences, 2021, 546: 349-367.
14	Rong M, Gong D W, Pedrycz W, et al. A multimodel prediction method for dynamic multiobjective evolutionary optimization[J]. IEEE Transactions on Evolutionary Computation, 2020, 24(2): 290-304.
15	李二超, 周扬. 基于分类的多策略预测方法求解动态多目标优化问题[J]. 控制与决策, 2021, 36(7): 1569-1580.
	Li Er-chao, Zhou Yang. A classification-based Multi-strategy prediction method for dynamic multi-objective optimization problems[J]. Control and Decision, 2021, 36(7): 1569-1580.
16	Xie H P, Zou J, Yang S X, et al. A decison variable classification-based cooperative coevolutionary algorithm for dynamic multiobjective optimization[J]. Information Sciences, 2021, 560: 307-330.
17	Zheng J, Zhou Y, Zou J, et al. A prediction strategy based on decision variable analysis for dynamic Multi-objective optimization[J]. Swarm and Evolutionary Computation, 2021, 60: No. 100786.
18	Muruganantham A, Tan K C, Vadakkepat P. Evolutionary dynamic multiobjective optimization via kalman filter prediction[J]. IEEE Transactions on Cybernetics, 2015, 46(12): 2862-2873.
19	李智翔, 李赟, 贺亮, 等. 使用新预测模型的动态多目标优化算法[J]. 西安交通大学学报, 2018, 52(10): 8-15.
	Li Zhi-xiang, Li Yun, He Liang, et al. A dynamic multiobjective optimization algorithm with a new prediction model[J]. Journal of Xi'an Jiaotong University, 2018, 52(10): 8-15.
20	Farina M, Deb K, Amato P. Dynamic multiobjective optimization problems[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(5): 425-442.
21	Kalman R E. A new approach to linear filtering and prediction problems[J]. Journal of basic Engineering, 1960, 82(1): 35-45.
22	Wu Y, Jin Y C, Liu X X. A directed search strategy for evolutionary dynamic multiobjective optimization[J]. Soft Computing, 2015, 19(11): 3221-3235.
23	Goh C K, Tan K C. A competitive-cooperative coevolutionary paradigm for dynamic multiobjective optimization[J]. IEEE Transactions on Evolutionary Computation, 2008, 13(1): 103-127.
24	Jiang S Y, Yang S X, Yao X, et al. Benchmark problems for CEC2018 competition on dynamic multiobjective optimisation[R]. United Kingdom: University of Birmingham, 2018.
25	Deb K, Karthik S. Dynamic multi-objective optimization and decision-making using modified NSGA-II: a case study on hydro-thermal power scheduling[C]∥International Conference on Evolutionary Multi-criterion Optimization, Berlin, Heidelberg, 2007: 803-817.
26	刘若辰, 李建霞, 刘静, 等. 动态多目标优化研究综述[J]. 计算机学报, 2020, 43(7): 1246-1278.
	Liu Ruo-chen, Li Jian-xia, Liu Jing, et al. A survey on dynamic multiobjective optimization[J]. Chinese Journal of Computers, 2020, 43(7): 1246-1278.
27	武燕, 石露露, 周艳. 动态多目标优化: 测试函数和算法比较[J]. 控制与决策, 2020, 35(10): 2372-2380.
	Wu Yan, Shi Lu-lu, Zhou Yan. Dynamic multi-objective optimization: test function and algorithm comparisons[J]. Control and Decision, 2020, 35(10): 2372-2380.
28	周爱民, 张青富, 张桂戌. 一种基于混合高斯模型的多目标进化算法[J]. 软件学报, 2014, 25(5): 913-928.
	Zhou Ai-min, Zhang Qing-fu, Zhang Gui-xu. Multiobjective evolutionary algorithm based on mixture Gaussian models[J]. Journal of Software, 2014, 25(5): 913-928.
29	李二超, 赵雨萌. 基于参考线的预测策略求解动态多目标优化问题[J]. 控制与决策, 2020, 35(7): 1547-1560.
	Li Er-chao, Zhou Yu-meng. Prediction strategy based on reference line for dynamic multi-objective optimization[J]. Control and Decision, 2020, 35(7): 1547-1560.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

测试函数	算法	MIGD（SD）	MIGD
测试函数	算法	MIGD（SD）	1^ststage	2^ndstage	3^rd stage
FDA1	DNSGA-Ⅱ	0.032 4（0.002 7）	0.056 8	0.027 3	0.009 6
	DSS	0.008 0（0.000 53）	0.011 8	0.006 9	0.007 1
	KFPS	0.007 4（0.000 29）	0.008 5	0.007 4	0.006 8
DMOP1	DNSGA-Ⅱ	0.048 8（0.009 8）	0.099 6	0.040 0	0.029 3
	DSS	0.025 1（0.007 9）	0.069 7	0.015 3	0.008 1
	KFPS	0.013 2（0.002 5）	0.012 9	0.015 5	0.007 6
DMOP2	DNSGA-Ⅱ	0.025 1（0.006 1）	0.022 9	0.027 3	0.020 8
	DSS	0.013 2（0.000 54）	0.010 2	0.016 0	0.007 6
	KFPS	0.012 7（0.000 19）	0.007 4	0.015 6	0.000 74
DF2	DNSGA-Ⅱ	0.021 2（0.008 4）	0.036 1	0.017 3	0.017 0
	DSS	0.010 1（0.000 67）	0.013 2	0.009 4	0.009 0
	KFPS	0.009 9（0.000 66）	0.009 5	0.010 0	0.009 5
DF3	DNSGA-Ⅱ	0.025 7（0.006 2）	0.173 8	0.063 0	0.011 6
	DSS	0.108 3（0.003 2）	0.055 4	0.020 5	0.011 2
	KFPS	0.018 1（0.000 11）	0.011 3	0.021 2	0.011 4
F5	DNSGA-Ⅱ	0.311 2（0.023 4）	0.611 2	0.286 6	0.103 4
	DSS	0.186 4（0.003 8）	0.206 3	0.198 2	0.172 9
	KFPS	0.155 1（0.019 0）	0.139 7	0.184 4	0.055 2
F6	DNSGA-Ⅱ	0.536 1（0.219 9）	0.872 8	0.373 8	0.239 8
	DSS	0.152 4（0.026 1）	0.135 1	0.145 2	0.179 5
	KFPS	0.118 5（0.016 0）	0.126 8	0.134 5	0.135 4
F7	DNSGA-Ⅱ	0.374 0（0.519 6）	0.319 2	0.341 6	0.158 5
	DSS	0.057 5（0.028 4）	0.089 6	0.050 9	0.045 9
	KFPS	0.087 4（0.052 1）	0.106 1	0.088 2	0.062 8

测试函数	算法	MIGD（SD）	MIGD
测试函数	算法	MIGD（SD）	1^ststage	2^ndstage	3^rd stage
FDA1	CKPS	0.027 6（0.003 60）	0.105 1	0.009 2	0.009 1
	PPS	0.052 8（0.009 13）	0.240 6	0.010 2	0.006 2
	KFPS	0.008 1（0.000 45）	0.008 2	0.007 5	0.007 1
DMOP1	CKPS	0.007 6（0.001 41）	0.018 3	0.005 1	0.005 1
	PPS	0.037 9（0.051 52）	0.141 3	0.020 9	0.005 7
	KFPS	0.018 9（0.002 5）	0.012 7	0.014 1	0.014 2
DMOP2	CKPS	0.027 2（0.006 11）	0.102 8	0.009 4	0.009 1
	PPS	0.060 7（0.010 23）	0.279 9	0.011 1	0.006 1
	KFPS	0.013 4（0.000 38）	0.011 0	0.014 1	0.013 8
FDA4	CKPS	0.021 2（0.001 65）	0.138 5	0.115 9	0.116 3
	PPS	0.130 7（0.002 05）	0.166 0	0.124 7	0.123 1
	KFPS	0.014 8（0.000 85）	0.009 5	0.014 5	0.015 0

测试函数	算法	MIGD
FDA1	PFMOP	0.0227
	RLPS	0.0137
	KFPS	0.0125
FDA2	PFMOP	0.1168
	RLPS	0.0518
	KFPS	0.0356
FDA3	PFMOP	0.2793
	RLPS	0.2753
	KFPS	0.5848
FDA4	PFMOP	0.0244
	RLPS	0.0228
	KFPS	0.0121
DMOP1	PFMOP	0.0088
	RLPS	0.0049
	KFPS	0.0158
DMOP2	PFMOP	0.0920
	RLPS	0.0693
	KFPS	0.0194

测试函数	DNSGA-Ⅱ	DSS	KFPS
FDA1	239	246	258
DMOP1	247	253	259
DMOP2	249	246	255
DF2	246	279	285
DF3	254	274	269

[1]	刘洲洲,张倩昀,马新华,彭寒. 基于优化离散差分进化算法的压缩感知信号重构[J]. 吉林大学学报(工学版), 2021, 51(6): 2246-2252.
[2]	徐卓君,杨雯婷,杨承志,田彦涛,王晓军. 雷达脉内调制识别的改进残差神经网络算法[J]. 吉林大学学报(工学版), 2021, 51(4): 1454-1460.
[3]	周炳海,吴琼. 基于多目标的机器人装配线平衡算法[J]. 吉林大学学报(工学版), 2021, 51(2): 720-727.
[4]	刘富,刘璐,侯涛,刘云. 基于优化MSR的夜间道路图像增强方法[J]. 吉林大学学报(工学版), 2021, 51(1): 323-330.
[5]	蒋磊,管仁初. 基于多目标进化算法的人才质量模糊综合评价系统设计[J]. 吉林大学学报(工学版), 2020, 50(5): 1856-1861.
[6]	周炳海,何朝旭. 基于线边集成超市的混流装配线动态物料配送调度[J]. 吉林大学学报(工学版), 2020, 50(5): 1809-1817.
[7]	陈磊,王江锋,谷远利,闫学东. 基于思维进化优化的多源交通数据融合算法[J]. 吉林大学学报(工学版), 2019, 49(3): 705-713.
[8]	刘富, 兰旭腾, 侯涛, 康冰, 刘云, 林彩霞. 基于优化k-mer频率的宏基因组聚类方法[J]. 吉林大学学报(工学版), 2018, 48(5): 1593-1599.
[9]	胡冠宇, 乔佩利. 基于云群的高维差分进化算法及其在网络安全态势预测上的应用[J]. 吉林大学学报(工学版), 2016, 46(2): 568-577.
[10]	李根，李文辉. 基于思维进化算法的人脸特征点跟踪[J]. 吉林大学学报(工学版), 2015, 45(2): 606-612.
[11]	李根, 李文辉. 基于思维进化的机器学习的遮挡人脸识别[J]. 吉林大学学报(工学版), 2014, 44(5): 1410-1416.
[12]	孔英秀, 赵丁选, 杨彬, 李天宇, 韩京元. 基于PSO-DE和LMI的鲁棒静态输出反馈控制[J]. 吉林大学学报(工学版), 2013, 43(05): 1375-1380.
[13]	丁辉, 李宏光. 求解约束多目标优化问题的Agent进化算法[J]. 吉林大学学报(工学版), 2011, 41(增刊1): 173-178.
[14]	田野, 刘大有, 齐红. 基于改进的单纯形和微分进化的混合优化算法[J]. 吉林大学学报(工学版), 2011, 41(02): 430-0434.
[15]	张利彪, 许相莉, 马铭, 孙彩堂, 周春光. 基于微分进化求解多目标优化问题中的退化现象[J]. 吉林大学学报(工学版), 2009, 39(04): 1041-1046.