基于多目标的机器人装配线平衡算法

doi:10.13229/j.cnki.jdxbgxb20190983

摘要/Abstract

摘要：

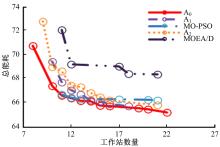
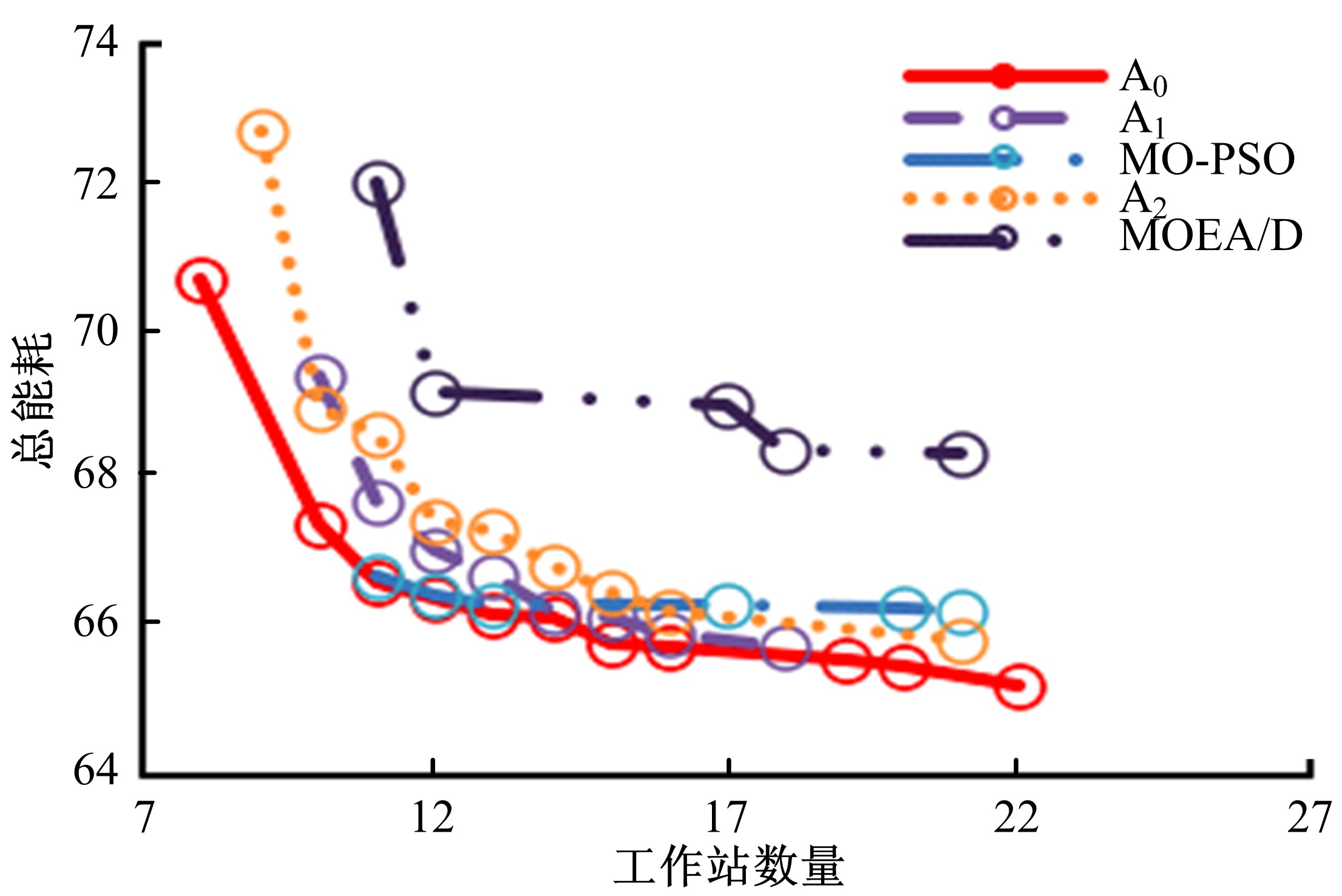
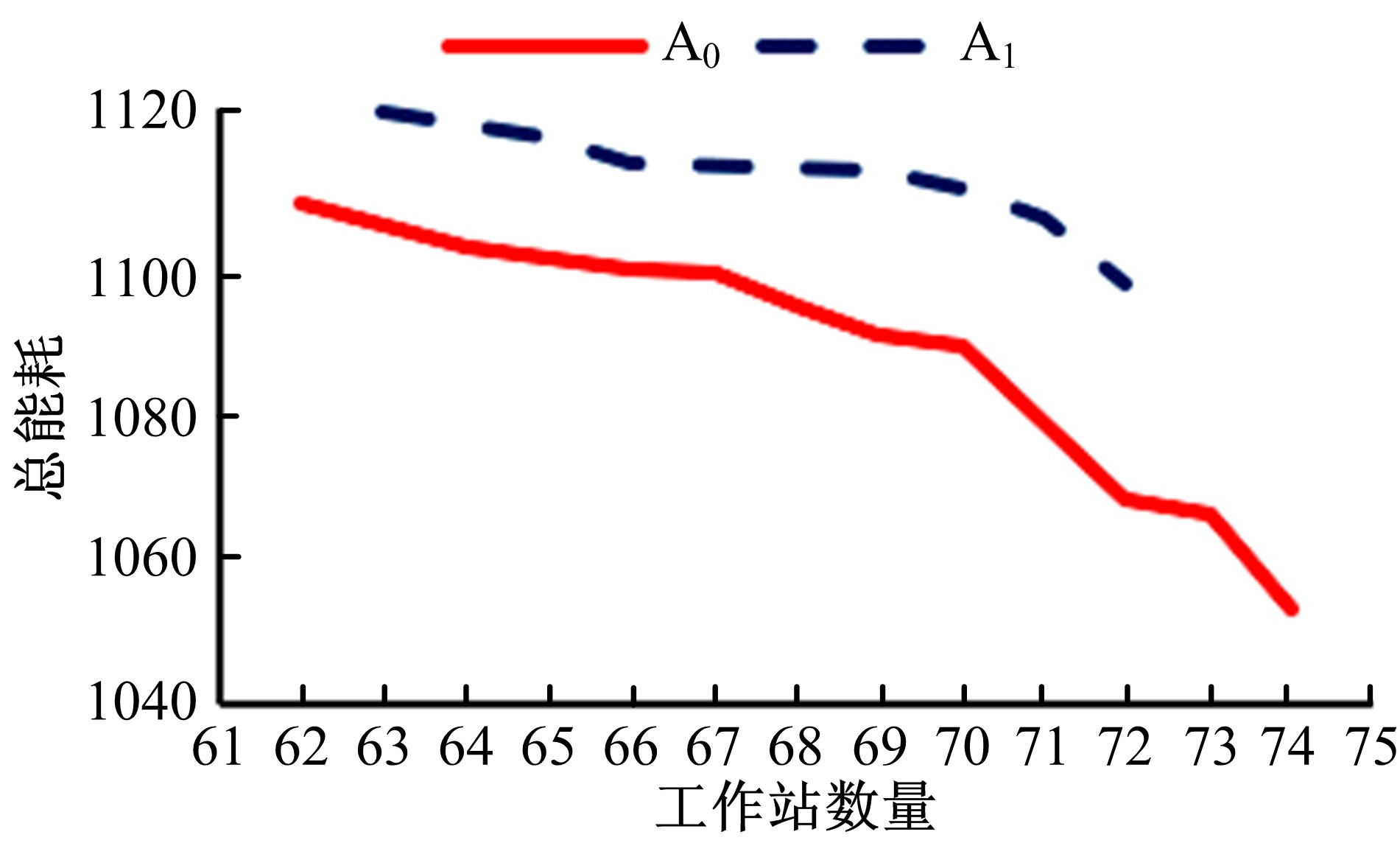
为提高装配线效率的同时优化制造的能源利用效率，在进行机器人装配线平衡时考虑机器人的执行能耗、换模能耗、待机能耗、工件传输能耗等，在工作站数量最小化和总能耗最小化两个目标之间寻求平衡。针对该约束的多目标优化问题，首先建立数学模型，设计编码方式；然后提出一种改进的基于分解的多目标进化算法，该算法引入非可行解参与进化和惩罚系数自适应变化策略以调节解的收敛性与多样性，并提出基于问题特殊性的局部搜索机制以进一步减小装配线能耗；最后对不同规模的问题进行优化，并与其他标杆算法进行对比，以评价该算法的效率和优越性。结果表明：该算法有效、可行，并且对该数学模型的求解有效提高了机器人装配线能效。

关键词: 计算机应用技术, 装配线平衡, 机器人, 能源, 多目标优化问题, 换模, 多目标进化算法

Abstract:

In order to improve the operation efficiency and the energy efficiency of the assembly line， the energy consumptions during task performing， changeover， stand-by and transportation were considered when balancing the robotic assembly lines. The objective was to minimize the number of workstations and the total energy consumption simultaneously. A mathematical model was first established， and then an improved Multi-objective Evolutionary Algorithm was proposed and a special coding scheme was designed. A constraint-handling technique， an adaptive penalty factor and a problem-based local search strategy were introduced to enhance the performance of the algorithm. Finally， the problems of different scales were optimized and the results were compared with other algorithms. The results show that the proposed algorithm is effective and feasible， and the energy efficiency of robotic assembly lines is improved.

Key words: computer applications, assembly line balancing, robot, energy, multi-objective optimization problem, changeover, multi-objective evolutionary algorithm

中图分类号:

TP29

周炳海,吴琼. 基于多目标的机器人装配线平衡算法[J]. 吉林大学学报(工学版), 2021, 51(2): 720-727.

Bing-hai ZHOU,Qiong WU. Balancing and bi⁃objective optimization of robotic assemble lines[J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(2): 720-727.

图/表 6

图1

图2

表1

表2

图3

图4

参考文献 17

1	Salahi N, Jafari M A. Energy-performance as a driver for optimal production planning[J]. Applied Energy, 2016, 174: 88-100.
2	Fysikopoulos A, Anagnostakis D, Salonitis K, et al. An empirical study of the energy consumption in automotive assembly[J]. Procedia CIRP, 2012, 3: 477-482.
3	Salveson M E. The assembly line balancing problem[J]. Journal of Industrial Engineering, 1955, 29(10): 55-101.
4	Rubinovitz J, Bukchin J, Lenz E. RALB-A heuristic algorithm for design and balancing of robotic assembly lines[J]. CIRP annals, 1993, 42(1): 497-500.
5	焦玉玲, 徐良成, 王占中, 等. 基于有向网络的双U型装配线平衡实验与分析[J]. 吉林大学学报: 工学版, 2018, 48(2): 454-459.
	Jiao Yu-ling, Xu Liang-cheng, Wang Zhan-zhong, et al. Balance experiment and analysis of double U-shaped assembly line based on directed network[J]. Journal of Jilin University (Engineering and Technology Edition), 2018, 48(2): 454-459.
6	周炳海, 吴琼. 考虑工具和空间约束的机器人装配线平衡优化[J]. 吉林大学学报: 工学版, 2019, 49(6): 2069-2075.
	Zhou Bing-hai, Wu Qiong. Balancing and optimization of robotic assemble lines with tool and space constraint[J]. Journal of Jilin University (Engineering and Technology Edition), 2019, 49(6): 2069-2075.
7	Nilakantan J M, Huang G Q, Ponnambalam S. An investigation on minimizing cycle time and total energy consumption in robotic assembly line systems[J]. Journal of Cleaner Production, 2015, 90: 311-325.
8	Nilakantan J M, Ponnambalam S. Robotic U-shaped assembly line balancing using particle swarm optimization[J]. Engineering Optimization, 2016, 48: 231-252.
9	Li Z X, Tang Q H, Zhang L P. Minimizing energy consumption and cycle time in two-sided robotic assembly line systems using restarted simulated annealing algorithm[J]. Journal of Cleaner Production,2016, 135: 508-522.
10	Feng L J, Ulutan D, Mears L. Energy consumption modeling and analyses in automotive manufacturing final assembly process[C]∥2015 IEEE Conference on Technologies for Sustainability. Ogden, UT, USA: IEEE, 2015: 224-228.
11	周炳海, 康雪云. 考虑切换时间的机器人装配线平衡优化方法[J]. 湖南大学学报: 自然科学版, 2017, 44(8): 35-42.
	Zhou Bing-hai, Kang Xue-yun. Optimal method of robotic assemble line balancing considering changeover time[J]. Journal of Hunan University (Natural Sciences), 2017, 44(8): 35-42.
12	He Y, Liu F, Wu T, et al. Analysis and estimation of energy consumption for numerical control machining[J]. Proceedings of the Institution of Mechanical Engineers Part B: Journal of Engineering Manufacture, 2012, 226(2): 255-266.
13	Zhang Q F, Li H. MOEA/D: a multiobjective evolutionary algorithm based on decomposition[J]. IEEE Transactions on Evolutionary Computation, 2008, 11(6): 712-731.
14	Jiang S Y, Yang S X. An improved multiobjective optimization evolutionary algorithm based on decomposition for complex pareto fronts[J]. IEEE Transactions on Cybernetics, 2016, 46(2): 421-437.
15	Bosman P A, Thierens D. The balance between proximity and diversity in multiobjective evolutionary algorithms[J]. IEEE Transactions on Evolutionary Computation, 2003, 7(2): 174-188.
16	Zitzler E, Thiele L. Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach[J]. IEEE Trans Evol Comput, 1999, 3(4): 257-271.
17	Gao J, Sun L Y, Wang L H, et al. An efficient approach for type II robotic assembly line balancing problems[J]. Computers and Industrial Engineering, 2009, 56(3): 1065-1080.

相关文章 15

[1]	许骞艺,秦贵和,孙铭会,孟诚训. 基于改进的ResNeSt驾驶员头部状态分类算法[J]. 吉林大学学报(工学版), 2021, 51(2): 704-711.
[2]	胡明伟,王洪光,潘新安. 基于正交设计的协作机器人全域结构优化设计[J]. 吉林大学学报(工学版), 2021, 51(1): 370-378.
[3]	宋元,周丹媛,石文昌. 增强OpenStack Swift云存储系统安全功能的方法[J]. 吉林大学学报(工学版), 2021, 51(1): 314-322.
[4]	蒋磊,管仁初. 基于多目标进化算法的人才质量模糊综合评价系统设计[J]. 吉林大学学报(工学版), 2020, 50(5): 1856-1861.
[5]	车翔玖,董有政. 基于多尺度信息融合的图像识别改进算法[J]. 吉林大学学报(工学版), 2020, 50(5): 1747-1754.
[6]	赵云伟,耿德旭,刘晓敏,刘齐. 气动柔性六足机器人定半径转弯实现方法与稳定性[J]. 吉林大学学报(工学版), 2020, 50(2): 472-482.
[7]	马芳武,倪利伟,吴量,聂家弘,徐广健. 轮腿式全地形移动机器人位姿闭环控制[J]. 吉林大学学报(工学版), 2019, 49(6): 1745-1755.
[8]	周炳海,吴琼. 考虑工具和空间约束的机器人装配线平衡优化[J]. 吉林大学学报(工学版), 2019, 49(6): 2069-2075.
[9]	温海营,任翔,徐卫良,丛明,秦文龙,胡书海. 咀嚼机器人颞下颌关节仿生设计及试验测试[J]. 吉林大学学报(工学版), 2019, 49(3): 943-952.
[10]	顾万里,王萍,胡云峰,蔡硕,陈虹. 具有H_∞性能的轮式移动机器人非线性控制器设计[J]. 吉林大学学报(工学版), 2018, 48(6): 1811-1819.
[11]	李战东,陶建国,罗阳,孙浩,丁亮,邓宗全. 核电水池推力附着机器人系统设计[J]. 吉林大学学报(工学版), 2018, 48(6): 1820-1826.
[12]	王林, 王洪光, 宋屹峰, 潘新安, 张宏志. 输电线路悬垂绝缘子清扫机器人行为规划[J]. 吉林大学学报(工学版), 2018, 48(2): 518-525.
[13]	栾文鹏, 刘永磊, 王鹏, 金志刚, 王健. 基于可信平台模块的能源互联网新型统一安全架构[J]. 吉林大学学报(工学版), 2017, 47(6): 1933-1938.
[14]	杨智勇, 吴功平, 王伟, 郭磊, 杨守东, 曹琪, 张义杰, 胡鹏. 高压巡检机器人下坡节能控速方法[J]. 吉林大学学报(工学版), 2017, 47(2): 567-576.
[15]	柴汇, 荣学文, 唐兴鹏, 李贻斌, 张勤, 李岳炀. 基于能量规划的崎岖地面四足机器人平面跳跃控制[J]. 吉林大学学报(工学版), 2017, 47(2): 557-566.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

算法	参数	小	中	大
AMOEA/D-ISB	种群大小	210	136	91
	进化代数	50	40	30
	向量邻居个数	15	15	14
	交叉概率	0.8	0.8	0.8
	变异概率	0.2	0.2	0.2
	权重更新参数	2	2	2
	局部搜索概率	0.6	0.6	0.6
MO-PSO	粒子群数	210	136	91
	迭代次数	50	40	30
	速度因子	0.1	0.1	0.1
	惯性影子	0.8	0.8	0.8
	交叉概率	0.8	0.8	0.8
	变异概率	0.2	0.2	0.2

问题规模	问题名称	指标	A₀	A₁	A₂	MO-PSO	MOEA/D
小规模	BUXEY (I=29)	IGD	0.1011	1.2960	1.4351	1.2166	3.0587
		HV	0.059	0.055	0.034	0.042	0.028
		N	11	8	9	6	5
		TIME	24.74	20.10	22.66	23.78	19.27
	LUTZ1 (I=32)	IGD	10.1726	12.3665	21.3557	13.5115	47.5169
		HV	0.041	0.022	0.037	0.029	0.006
		N	6	5	4	4	3
		TIME	38.00	34.71	32.32	34.02	30.25
中规模	HAHN (I=53)	IGD	10.0403	17.8439	90.0004	32.4227	100.5772
		HV	0.023	0.012	0.005	0.012	0.001
		N	11	7	8	7	4
		TIME	34.68	28.48	27.27	30.59	24.06
	ARC83 (I=83)	IGD	29.3147	135.052	177.9932	146.5395	514.7043
		HV	0.61	0.24	0.21	0.25	0.16
		N	8	5	6	5	3
		TIME	96.93	61.37	55.52	60.77	46.22
大规模	ARC111 (I=111)	IGD	58.9270	78.6921	137.3280	93.3462	202.0398
		HV	0.022	0.019	0.017	0.017	0.015
		N	10	6	11	7	5
		TIME	79.96	66.86	63.54	68.49	49.23
	BARTHOL2 (I=148)	IGD	8.0221	10.1641	16.3182	12.4029	43.0122
		HV	0.19	0.13	0.08	0.11	0.02
		N	10	6	7	5	4
		TIME	209.47	122.80	115.91	112.94	77.85
均值		IGD	19.4297	42.5692	74.0718	49.9066	151.8182
		HV	0.158	0.080	0.064	0.077	0.038
		N	9	6	8	6	4
		TIME	80.63	55.72	52.87	55.10	41.15