吉林大学学报(工学版) ›› 2019, Vol. 49 ›› Issue (5): 1706-1714.doi: 10.13229/j.cnki.jdxbgxb20180357

• • 上一篇    

非均匀噪声条件下考虑互耦效应的DOA估计方法

王洪雁1,2(),房云飞1,2,朱圣棋3,裴炳南1,2   

  1. 1. 大连大学 辽宁省北斗高精度位置服务技术工程实验室，辽宁 大连 116622
    2. 大连大学 大连市环境感知与智能控制重点实验室，辽宁 大连 116622
    3. 西安电子科技大学 雷达信号处理国家重点实验室，西安 710071
  • 收稿日期:2018-04-17 出版日期:2019-09-01 发布日期:2019-09-11
  • 作者简介:王洪雁（1979-），男，副教授，博士.研究方向：MIMO雷达，毫米波通信.E-mail:gglongs@163.com
  • 基金资助:
    国家自然科学基金项目(61301258);中国博士后科学基金项目(2016M590218);雷达认知探测成像识别学科创新引智基地项目(B18039)

DOA estimation method considering mutual coupling effect in presence of non⁃uniform noise

Hong-yan WANG1,2(),Yun-fei FANG1,2,Sheng-qi ZHU3,Bing-nan PEI1,2   

  1. 1. Liaoning Engineering Laboratory of BeiDou High-Precision Location Service, Dalian University, Dalian 116622, China
    2. Dalian Key Laboratory of Environmental Perception and Intelligent Control, Dalian University, Dalian 116622, China
    3. National Lab of Radar Signal Processing, Xidian University, Xi′an 710071, China
  • Received:2018-04-17 Online:2019-09-01 Published:2019-09-11

RICH HTML

 5   

PDF (PC)

282

摘要：

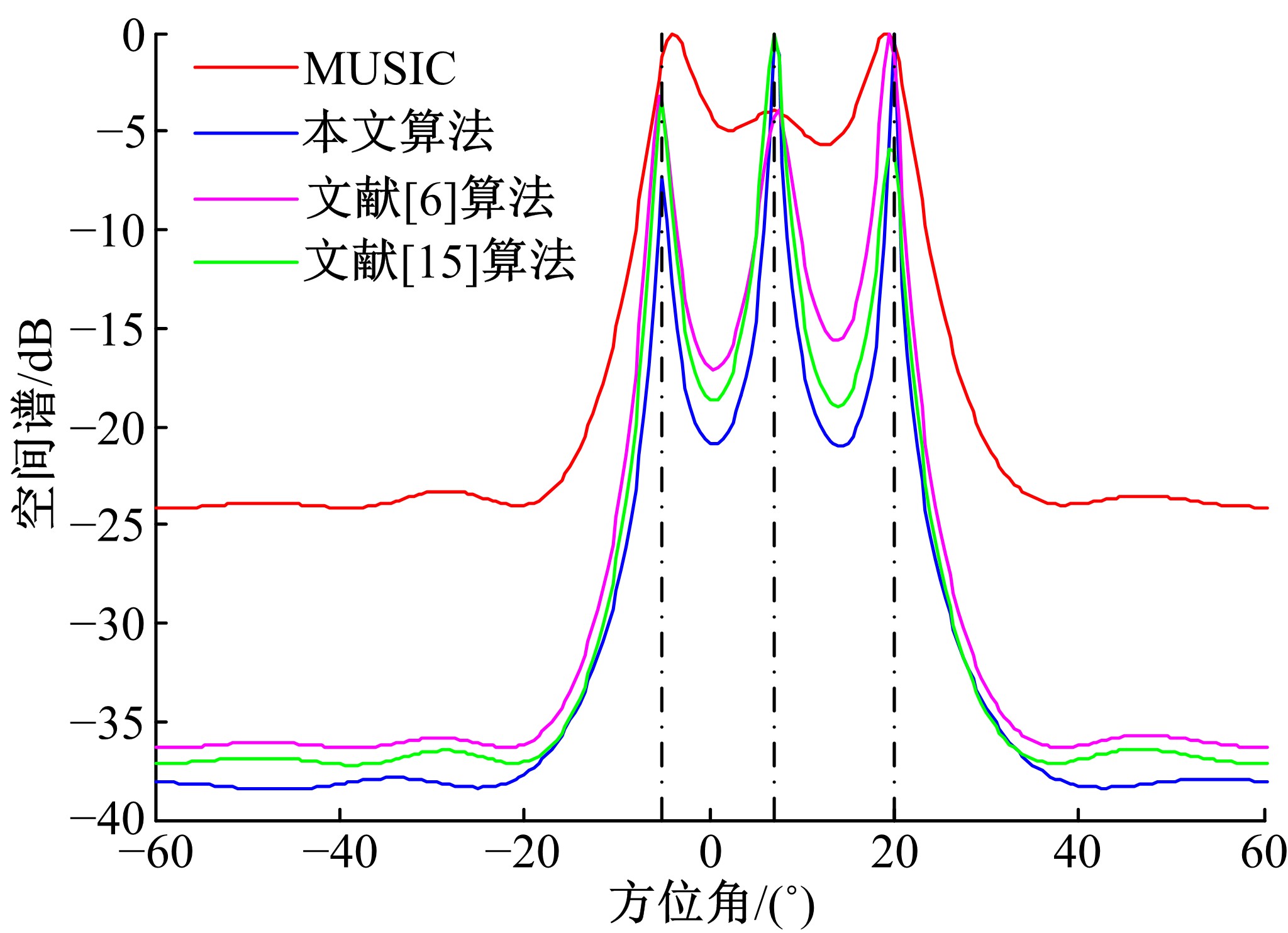
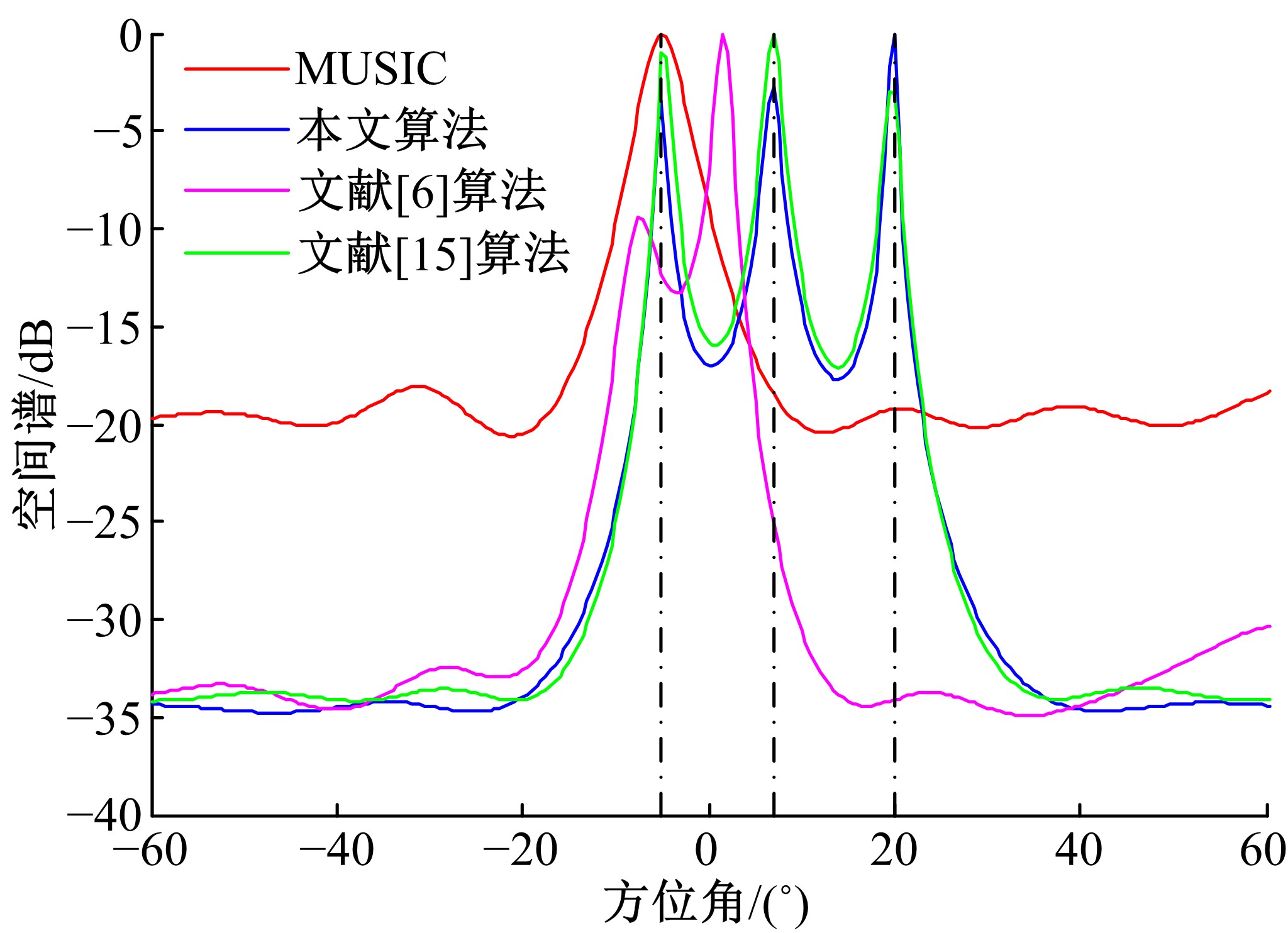
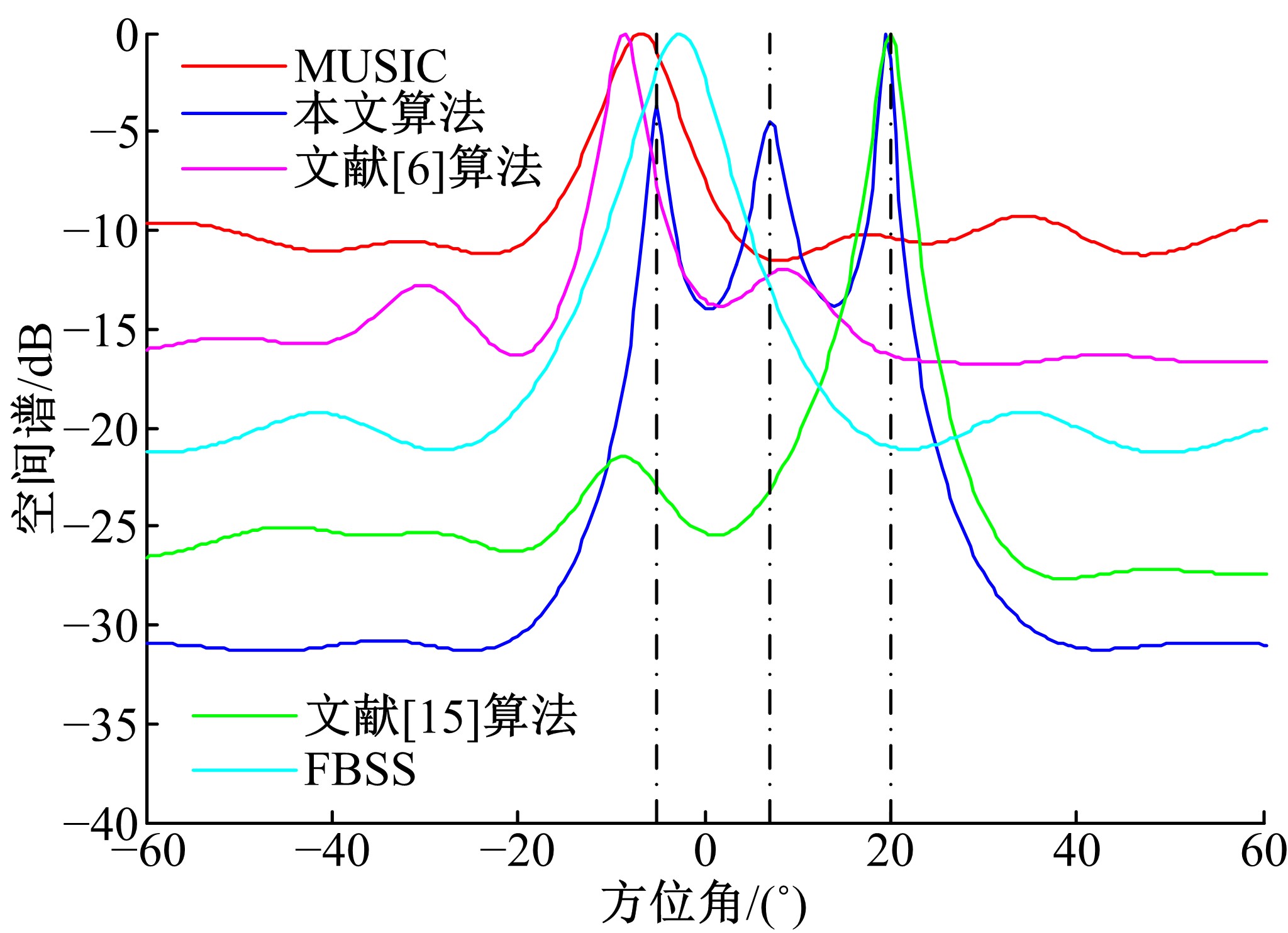
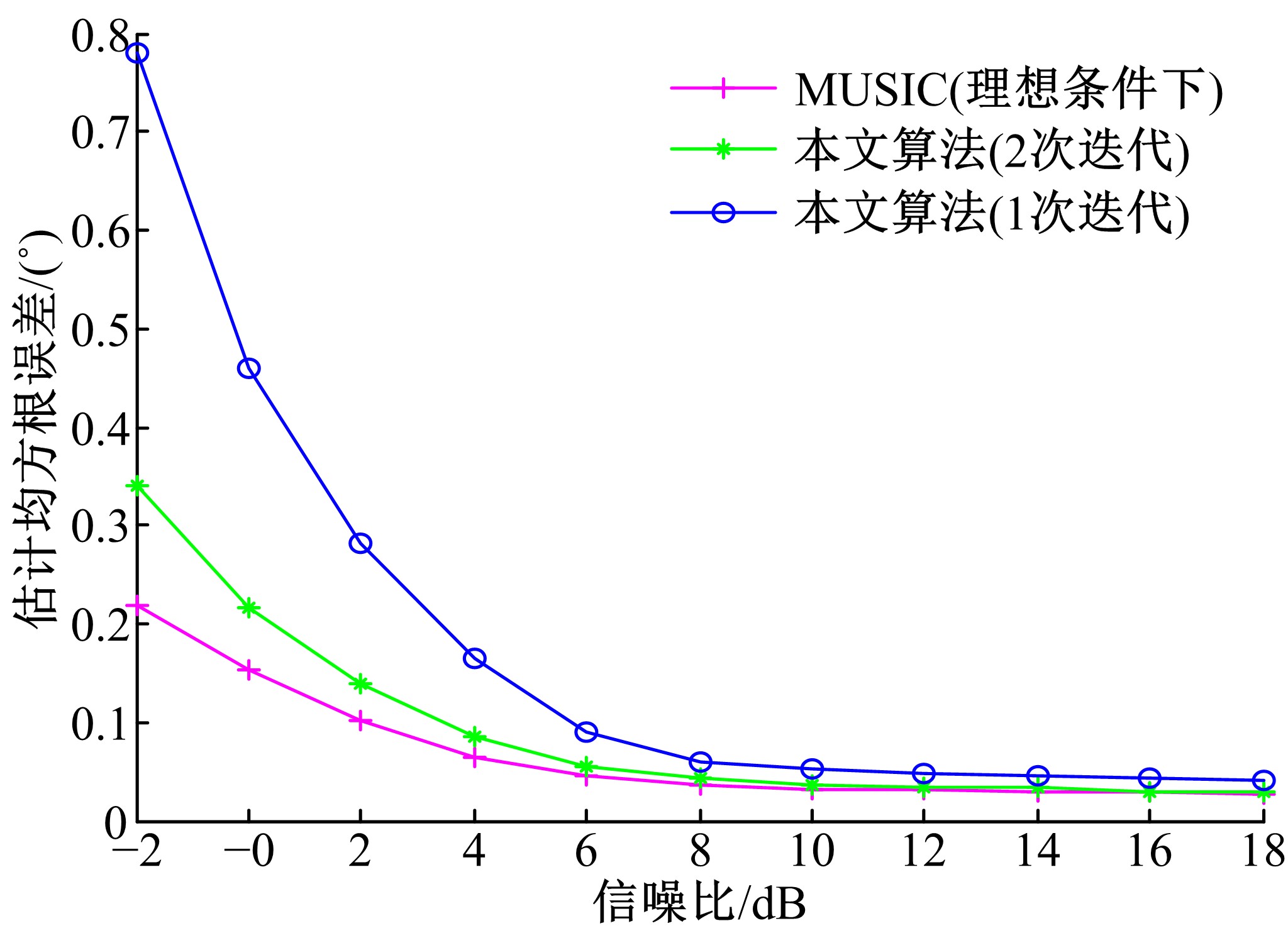
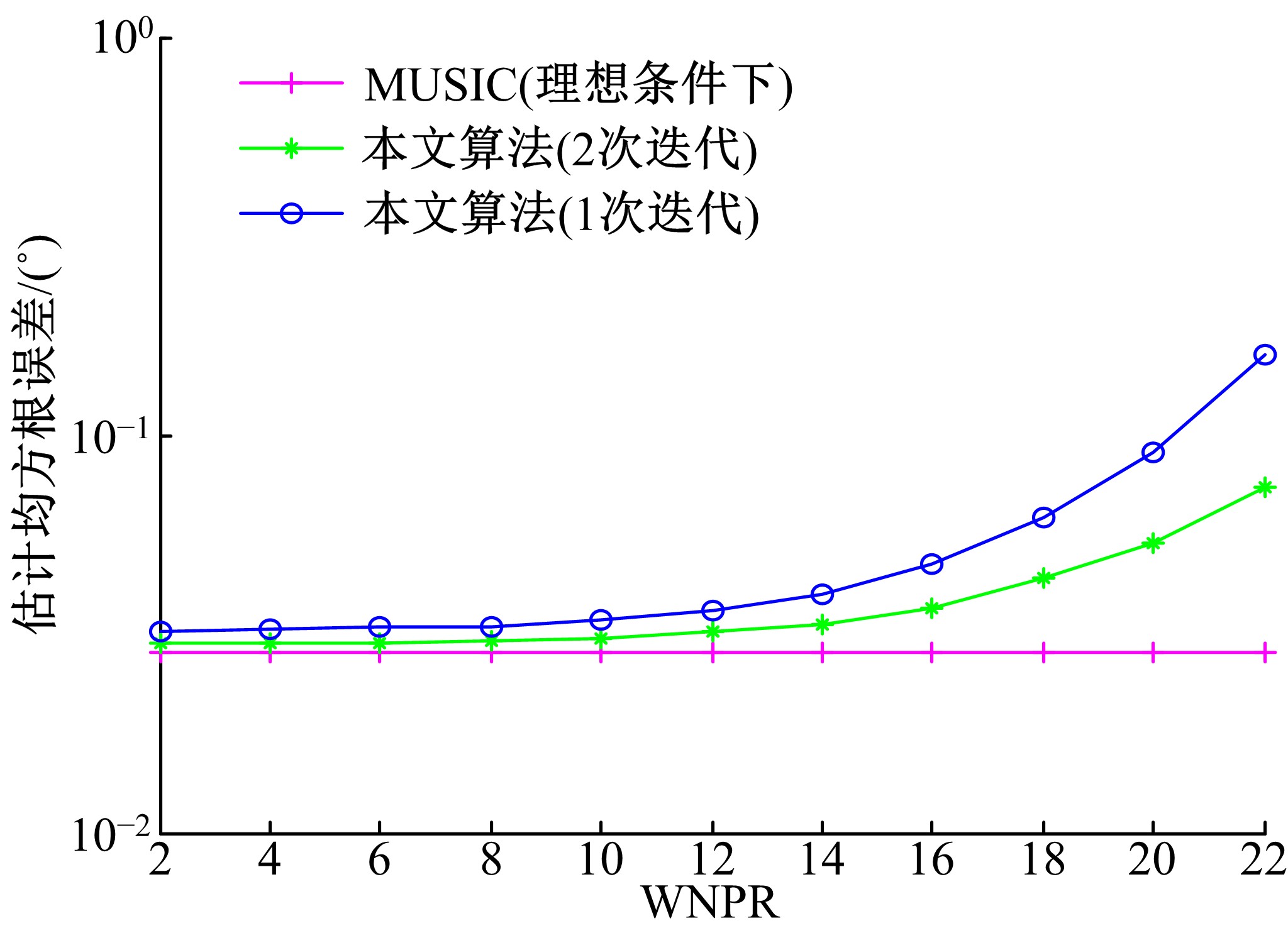
针对非均匀噪声和互耦条件下相干信号辨识性能较差的问题，提出一种基于非均匀噪声协方差矩阵和互耦系数重构的DOA估计方法。首先，利用最小二乘理论并通过迭代优化方法恢复互耦意义下的无噪声信号协方差矩阵；然后，依据信号子空间原理，并通过估计不相关信号角度重构互耦系数矩阵，进而获得互耦补偿后的无噪声信号协方差矩阵；最后，通过传统空间平滑方法获得解相干信号，并利用MUSIC算法实现DOA参数估计。数值仿真表明：与仅考虑相干信源、非均匀噪声或互耦的传统DOA估计算法相比，本文算法可较好地抑制非均匀噪声，克服了互耦场景下传统空间平滑算法解相干失效问题，并可显著改善非均匀噪声和互耦条件下相干信源的DOA估计性能。

关键词: 通信技术, 波达方向, 非均匀噪声, 互耦, 相干信源, 空间平滑, 最小二乘

Abstract:

To solve the problem of poor identification performance of coherent signals in the presences of non-uniform noise and mutual coupling, a Direction of Arrival (DOA) estimation method based on non-uniform noise covariance matrix and mutual coupling coefficient reconstruction is proposed in this paper. Using the Least Squares (LS) theory, the noise-free covariance matrix in the sense of mutual coupling can be recovered by iterative optimization approach. Then, the uncorrelated signals angle determined by applying the principle of signal subspace can be used to reconstruct the mutual coupling matrix, so that the noise-free signal covariance matrix after compensating the mutual coupling can be obtained. Finally, the spatial smoothing techniques can be employed to decorrelate the coherent signals, which enable us to apply the MUSIC algorithm to achieve DOA estimation. Simulation results demonstrate that, compared to the traditional MUSIC and DOA estimation algorithms, which only considers coherent signals, non-uniform noise or mutual coupling, the proposed method can suppress non-uniform noise significantly, overcome the decorrelation failure of the conventional spatial smoothing techniques in the case of mutual coupling, and improve the DOA estimation performance of coherent signals under the coexistence of both non-uniform noise and mutual coupling considerably.

Key words: communication technology, direction of arrival, non-uniform noise, mutual coupling, coherent signals, spatial smoothing, least-squares

中图分类号: 

  • TN911

图1

非均匀噪声条件下非相干信号空域谱（互耦已知）"

图2

非均匀噪声及互耦条件下非相干信号空域谱"

图3

非均匀噪声及互耦条件下相干信号空域谱"

图4

RMSE随信噪比SNR变化对比"

图5

RMSE随WNPR变化对比"

1 Qiao H , Pal P . On maximum-likelihood methods for localizing more sources than sensors[J]. IEEE Signal Processing Letters, 2017, 24(5): 703-706.
2 Wang Q , Dou T , Chen H , et al . Effective block sparse representation algorithm for DOA estimation with unknown mutual coupling[J]. IEEE Communications Letters, 2017, 21(12): 2622-2625.
3 Schmidt R . Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas & Propagation, 1986, 34(3): 276-280.
4 Liao B , Chan S C , Huang L , et al . Iterative methods for subspace and DOA estimation in nonuniform noise[J]. IEEE Transactions on Signal Processing, 2016, 64(12): 3008-3020.
5 Tian Y , Shi H , Xu H . DOA estimation in the presence of unknown nonuniform noise with coprime array[J]. Electronics Letters, 2016, 53(2): 113-115.
6 Wen J , Liao B , Guo C . Spatial smoothing based methods for direction-of-arrival estimation of coherent signals in nonuniform noise[J]. Digital Signal Processing, 2017, 67(1): 116-122.
7 Ma X , Dong X , Xie Y . An improved spatial differencing method for DOA estimation with the coexistence of uncorrelated and coherent signals[J]. IEEE Sensors Journal, 2016, 16(10): 3719-3723.
8 石要武, 陈淼, 单泽涛, 等 . 基于特征空间MUSIC算法的相干信号波达方向空间平滑估计[J]. 吉林大学学报: 工学版, 2017, 47(1): 268-273.
Shi Yao-wu , Chen Miao , Shan Ze-tao , et al . Spatial smoothing technique for coherent signal DOA estimation based on eigen space MUSIC algorithm[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(1): 268-273.
9 Dai J , Ye Z . Spatial smoothing for direction of arrival estimation of coherent signals in the presence of unknown mutual coupling[J]. IET Signal Processing, 2011, 5(4): 418-425.
10 Mao W , Li G , Xie X , et al . DOA estimation of coherent signals based on direct data domain under unknown mutual coupling[J]. IEEE Antennas and Wireless Propagation Letters, 2014, 13(1): 1525-1528.
11 Liao B , Zhang Z G , Chan S C . DOA estimation and tracking of ULAs with mutual coupling[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 891-905.
12 He Z Q , Shi Z P , Huang L . Covariance sparsity-aware DOA estimation for nonuniform noise[J]. Digital Signal Processing, 2014, 28(1): 75-81.
13 Pillai S U , Kwon B H . Forward/backward spatial smoothing techniques for coherent signal identification[J]. IEEE Transactions on Acoustics Speech and Signal Processing, 1989, 37(1): 8-15.
14 Liu F , Wang J , Sun C , et al . Spatial differencing method for DOA estimation under the coexistence of both uncorrelated and coherent signals[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(4): 2052-2062.
15 Liao B , Huang L , Chan S C . DOA estimation under the coexistence of nonuniform noise and mutual coupling,[C] ∥2015 IEEE China Summit and International Conference on Signal and Information Processing (China SIP), Chengdu China, 2015: 731-735.
16 Ye Z , Liu C . On the resiliency of MUSIC direction finding against antenna sensor coupling[J]. IEEE Transactions on Antennas and Propagation, 2008, 56(2): 371-380.
17 Horn R A , Johnson C R . Matrix Analysis[M]. Cambridge, U K: Cambridge University Press, 1985.
18 Tropp J A , Dhillon I S , Heath R W , et al . Designing structured tight frames via an alternating projection method[J]. IEEE Transactions on information theory, 2005, 51(1): 188-209.
19 单泽涛, 刘小松, 单泽彪, 等 . 基于改进平滑l 0范数的DOA估计算法[J]. 吉林大学学报: 信息科学版, 2017, 35(6): 603-607.
Shan Ze-tao , Liu Xiao-song , Shan Ze-biao , et al . DOA estimation algorithm based on improved smoothed l 0 norm[J]. Journal of Jilin University (Information Science Edition), 2017, 35(6): 603-607.
[1] 李文军,华强,谭立东,孙悦. DV⁃HOP和接收信号强度指示结合的改进算法[J]. 吉林大学学报(工学版), 2019, 49(5): 1689-1695.
[2] 刘勇,邓方顺,刘小林,闵思婕,王鹏. 基于双混沌振子的最小频移键控信号频率估计方法[J]. 吉林大学学报(工学版), 2019, 49(4): 1357-1362.
[3] 王宏志,姜方达,周明月. 基于遗传粒子群优化算法的认知无线电系统功率分配[J]. 吉林大学学报(工学版), 2019, 49(4): 1363-1368.
[4] 周彦果,张海林,陈瑞瑞,周韬. 协作网络中采用双层博弈的资源分配方案[J]. 吉林大学学报(工学版), 2018, 48(6): 1879-1886.
[5] 单泽彪,刘小松,史红伟,王春阳,石要武. 动态压缩感知波达方向跟踪算法[J]. 吉林大学学报(工学版), 2018, 48(6): 1938-1944.
[6] 隗海林, 包翠竹, 李洪雪, 李明达. 基于最小二乘支持向量机的怠速时间预测[J]. 吉林大学学报(工学版), 2018, 48(5): 1360-1365.
[7] 牟宗磊, 宋萍, 翟亚宇, 陈晓笑. 分布式测试系统同步触发脉冲传输时延的高精度测量方法[J]. 吉林大学学报(工学版), 2018, 48(4): 1274-1281.
[8] 丁宁, 常玉春, 赵健博, 王超, 杨小天. 基于USB 3.0的高速CMOS图像传感器数据采集系统[J]. 吉林大学学报(工学版), 2018, 48(4): 1298-1304.
[9] 孙晓颖, 扈泽正, 杨锦鹏. 基于分层贝叶斯网络的车辆发动机系统电磁脉冲敏感度评估[J]. 吉林大学学报(工学版), 2018, 48(4): 1254-1264.
[10] 董颖, 崔梦瑶, 吴昊, 王雨后. 基于能量预测的分簇可充电无线传感器网络充电调度[J]. 吉林大学学报(工学版), 2018, 48(4): 1265-1273.
[11] 陈涛, 崔岳寒, 郭立民. 适用于单快拍的多重信号分类改进算法[J]. 吉林大学学报(工学版), 2018, 48(3): 952-956.
[12] 田彦涛, 张宇, 王晓玉, 陈华. 基于平方根无迹卡尔曼滤波算法的电动汽车质心侧偏角估计[J]. 吉林大学学报(工学版), 2018, 48(3): 845-852.
[13] 关济实, 石要武, 邱建文, 单泽彪, 史红伟. α稳定分布特征指数估计算法[J]. 吉林大学学报(工学版), 2018, 48(2): 618-624.
[14] 陈瑞瑞, 张海林. 三维毫米波通信系统的性能分析[J]. 吉林大学学报(工学版), 2018, 48(2): 605-609.
[15] 张超逸, 李金海, 阎跃鹏. 双门限唐检测改进算法[J]. 吉林大学学报(工学版), 2018, 48(2): 610-617.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
版权所有 © 《吉林大学学报(工学版)》编辑部
地址：长春市人民大街5988号　电话：+86-431-85095297　传真：+86-431-85094074　E-mail: xbgxb@jlu.edu.cn
本系统由北京玛格泰克科技发展有限公司设计开发