吉林大学学报(工学版) ›› 2022, Vol. 52 ›› Issue (2): 384-391.doi: 10.13229/j.cnki.jdxbgxb20211089
• 车辆工程·机械工程 • 上一篇
基于向量投影响应面的数控机床几何误差分配方法
章子玲1( ),胡雄1,亓寅2,王微1,陶志强3,刘志峰4,5(
),胡雄1,亓寅2,王微1,陶志强3,刘志峰4,5( )
)
- 1.上海海事大学 物流工程学院,上海 201306
2.鹰潭市技工学校,鹰潭 335001
3.北京联合大学 机器人学院,北京 100027
4.吉林大学 数控装备可靠性教育部重点实验室,长春 130022
5.吉林大学 机械与航空航天工程学院,长春 130022
An approach for error allocation of machine tool based on vector projection response surface method
Zi-ling ZHANG1( ),Xiong HU1,Yin QI2,Wei WANG1,Zhi-qiang TAO3,Zhi-feng LIU4,5(
),Xiong HU1,Yin QI2,Wei WANG1,Zhi-qiang TAO3,Zhi-feng LIU4,5( )
)
- 1.Logistics Engineering College,Shanghai Maritime University,Shanghai 201306,China
2.Yingtan Vocational and Technical College,Yingtan,335001,China
3.College of Robotics,Beijing Union University,Beijing 100027,China
4.Key Laboratory of CNC Equipment Reliability,Ministry of Education,Jilin University,Changchun 130022,China
5.School of Mechanical and Aerospace Engineering,Jilin University,Changchun 130012,China
摘要:
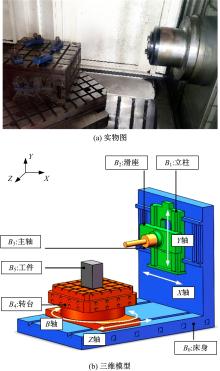
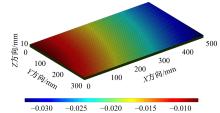
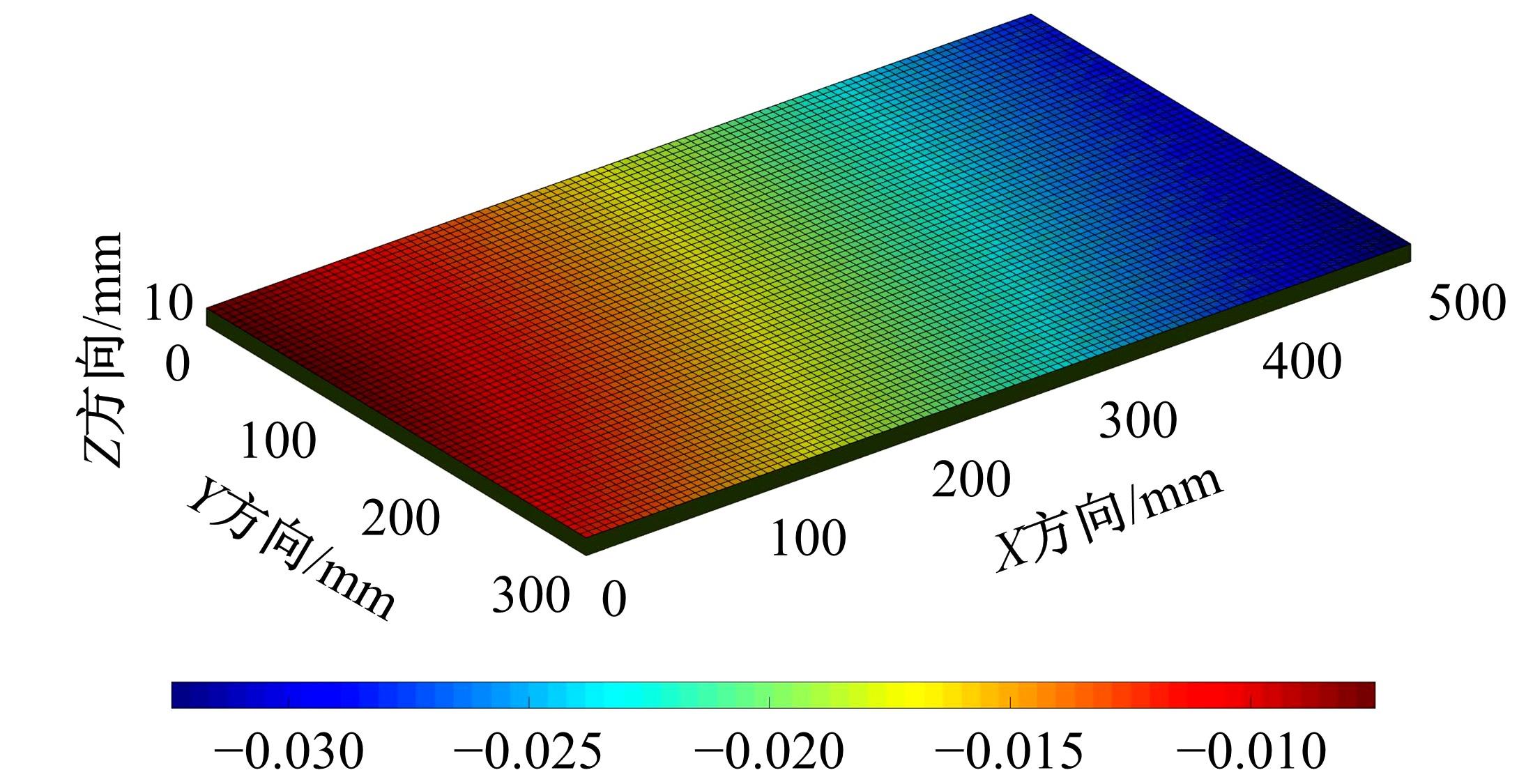
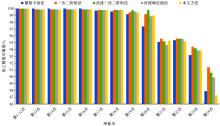
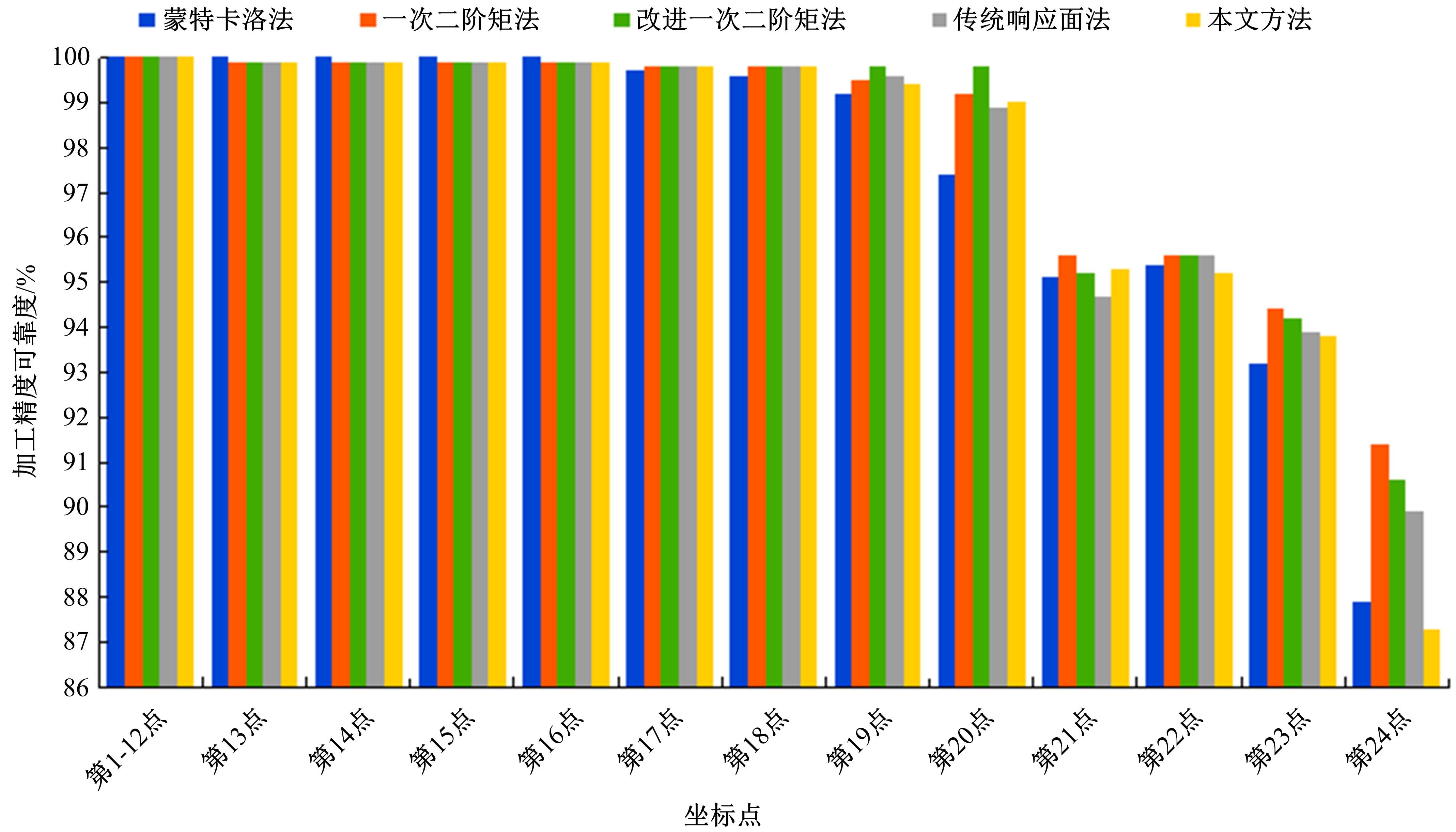
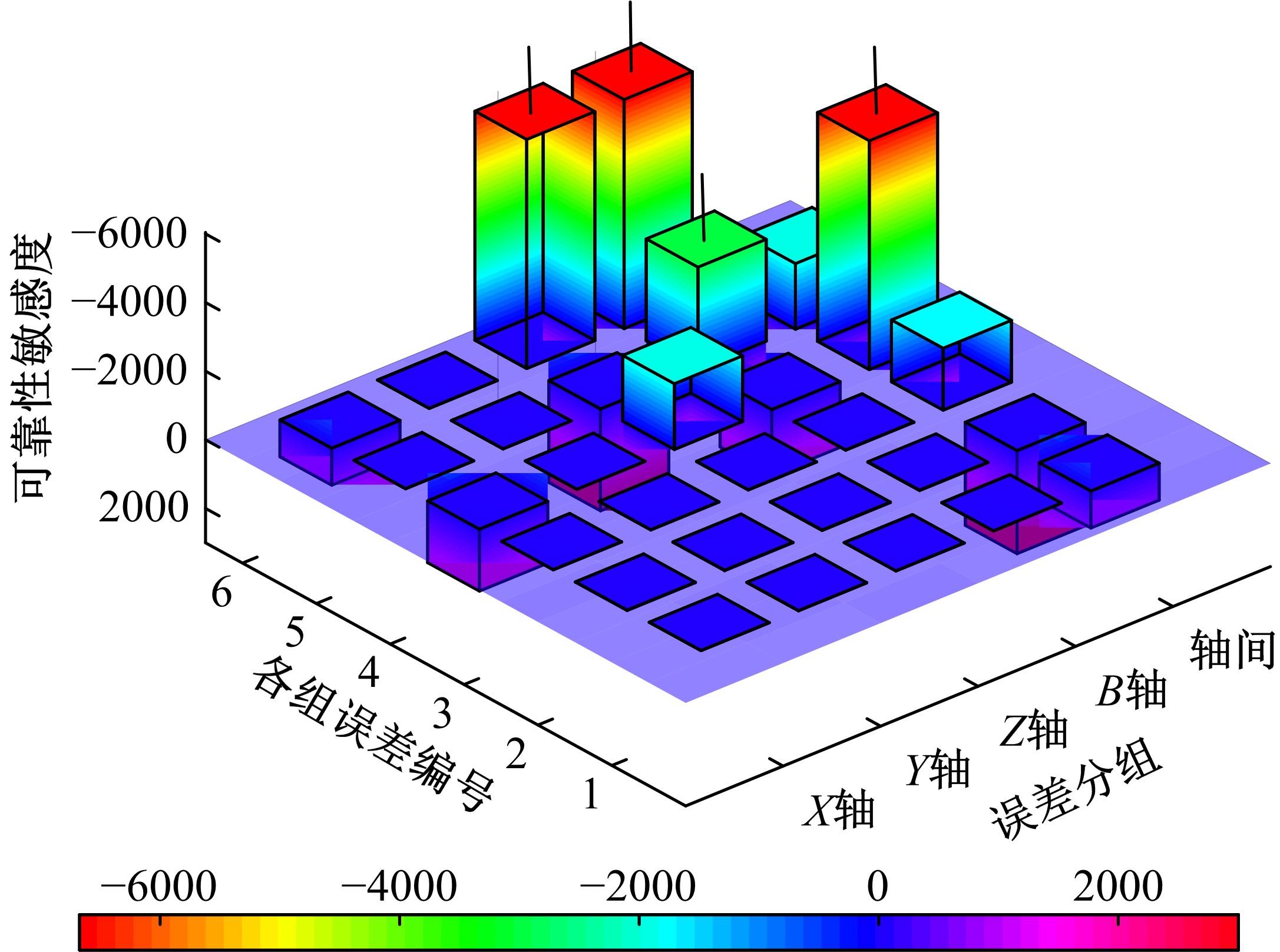
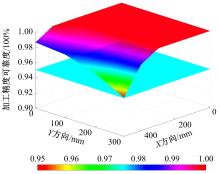
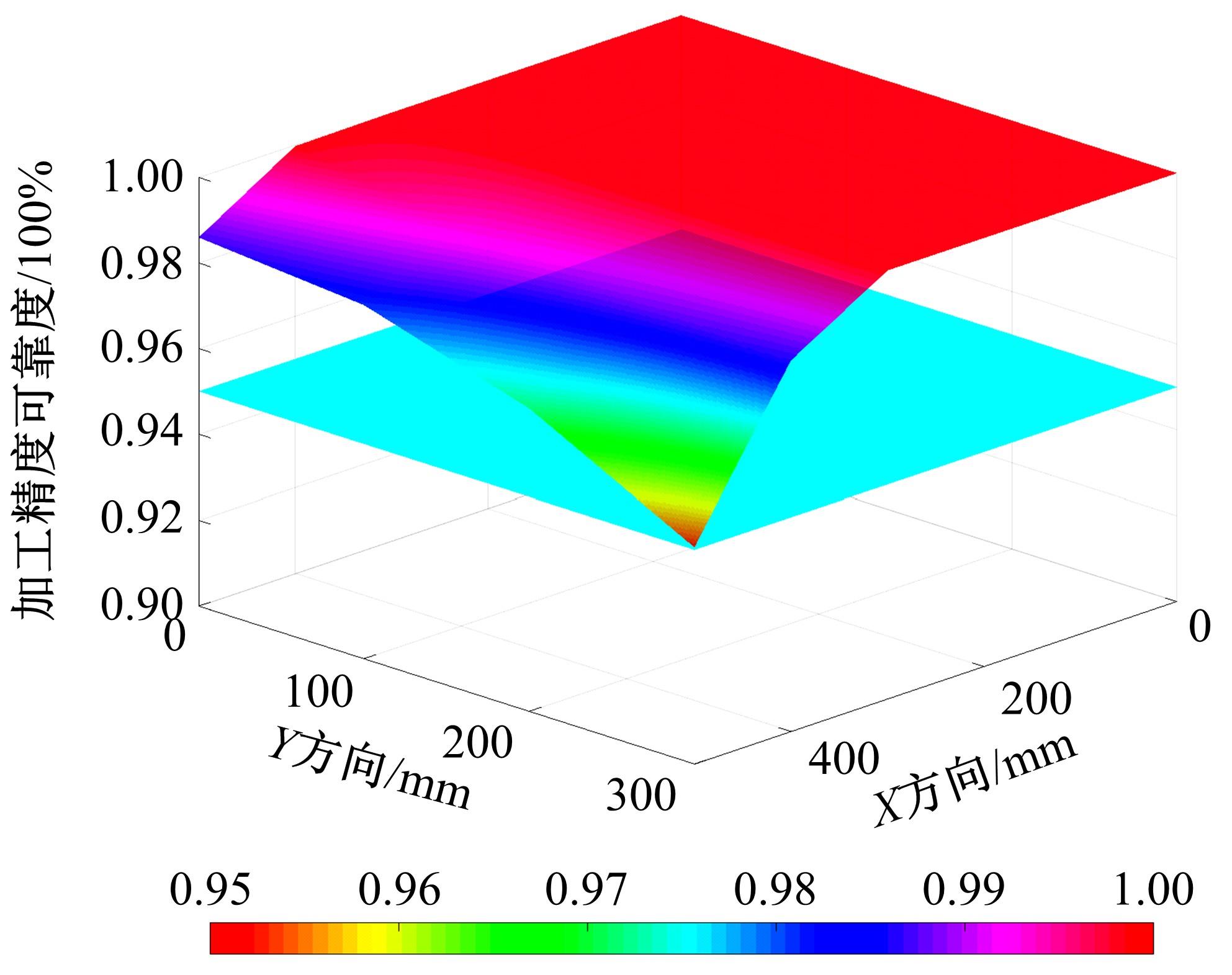
以几何误差为研究对象,基于多体系统理论,建立了数控机床综合误差模型;运用向量投影响应面法,建立了加工精度可靠度模型和可靠性敏感度模型,以评估加工精度可靠度并获取几何误差分布参数对可靠度的影响排序,实现几何误差参数的合理优化和可靠度的整体提升。最后,通过案例分析验证了该方法的正确性。
中图分类号:
- TH161
| 1 | Zhang Zi-ling, Liu Zhi-feng, Cai Li-gang, et al. An accuracy design approach for a multi-axis NC machine tool based on reliability theory[J]. The International Journal of Advanced Manufacturing Technology, 2017, 91(5-8): 1547-1566. |
| 2 | Zhang Zi-ling, Qi Yin, Cheng Qiang, et al. Machining accuracy reliability during the peripheral milling process of thin-walled components[J]. Robotics and Computer Integrated Manufacturing, 2019, 59: 222-234. |
| 3 | 刘志峰, 刘广博, 程强, 等. 基于多体系统理论的精密立式加工中心精度建模与预测[J]. 吉林大学学报: 工学版, 2012, 42(2): 388-391. |
| Liu Zhi-feng, Liu Guang-bo, Cheng Qiang, et al. Precision modeling and prediction of precise vertical machining center based on theory of multi-body system[J]. Journal of Jilin University(Engineering and Technology Edition), 2012, 42(2): 388-391. | |
| 4 | Cai Li-gang, Zhang Zi-ling, Cheng Qiang, et al. A geometric accuracy design method of multi-axis NC machine tool for improving machining accuracy reliability[J]. Eksploatacja I Niezawodnosc-Maintenance and Reliability, 2015, 17(1): 143-155. |
| 5 | Cai Li-gang, Zhang Zi-ling, Cheng Qiang, et al. An approach to optimize the machining accuracy retainability of multi-axis NC machine tool based on robust design[J]. Precision Engineering-Journal of the International Societies for Precision Engineering and Nanotechnology, 2016, 43: 370-386. |
| 6 | 曲兴田, 赵永兵, 刘海忠, 等. 基串并混联机床几何误差建模与实验[J]. 吉林大学学报: 工学版, 2017, 47(1): 137-144. |
| Qu Xing-tian, Zhao Yong-bing, Liu Hai-zhong, et al. Modeling and experiment of spatial geometric errors of hybrid serial parallel machine tool[J]. Journal of Jilin University(Engineering and Technology Edition), 2017, 47(1): 137-144. | |
| 7 | 李国龙, 陶小会, 徐凯, 等. 数控机床转台位置相关几何误差的快速测量与辨识[J]. 吉林大学学报: 工学版, 2021, 51(2): 458-467. |
| Li Guo-long, Tao Xiao-hui, Xu Kai, et al. Rapid measurement and identification of position dependent geometric errors of CNC machine tool turntable[J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(2): 458-467. | |
| 8 | 李圣一, 戴一帆, 尹自强, 等. 精密和超精密机床精度建模技术[M]. 长沙: 国防科技大学出版社, 2007. |
| 9 | Helton J C, Johnson J D, Sallaberry C J, et al. Survey of sampling-based methods for uncertainty and sensitivity analysis[J]. Reliability Engineering & System Safety, 2006, 91(10/11): 1175-1209. |
| 10 | 吕震宙, 宋述芳, 李洪双, 等. 结构机构可靠性及可靠性灵敏度分析[M]. 北京: 科学出版社, 2009. |
| 11 | 郑财, 黄贤振, 胡明伟, 等. 三轴数控机床加工精度可靠性分析[J]. 机床与液压, 2017, 45(15): 180-183, 160. |
| Zheng Cai, Huang Xian-zhen, Hu Ming-wei, et al. Three axis NC machine tool machining accuracy reliability analysis[J]. Machine Tool & Hydraulics, 2017, 45(15): 180-183, 160. | |
| 12 | Zhang Zi-ling, Cai Li-gang, Cheng Qiang, et al. A geometric error budget method to improve machining accuracy reliability of multi-axis machine tools[J]. Journal of Intelligent Manufacturing, 2019, 30(2): 495-519. |
| 13 | 余治民, 刘子建, 艾彦迪, 等. 大型数控龙门导轨磨床几何误差建模与基于可靠性理论的精度分配[J]. 机械工程学报, 2013, 17: 142-151. |
| Yu Zhi-min, Liu Zi-jian, Ai Yan-di, et al. Geometric error model and precision distribution based on reliability theory for large CNC gantry guideway grinder[J]. Journal of Mechanical Engineering, 2013, 17: 142-151. | |
| 14 | 孙志礼,张义民,何雪浤,等. 数控机床性能分析及可靠性设计技术[M]. 北京: 机械工业出版社, 2011. |
| 15 | Cheng Qiang, Zhao Hong-wei, Zhao Yong-sheng, et al. Machining accuracy reliability analysis of multi-axis machine tool based on Monte Carlo simulation[J]. Journal of Intelligent Manufacturing, 2018, 29(1): 191-209. |
| 16 | Zhang Zi-ling, Cheng Qiang, Qi Bao-bao, et al. A general approach for the machining quality evaluation of S-shaped specimen based on POS-SQP algorithm and monte carlo method[J]. Journal of Manufacturing Systems, 2021, 60: 553-568. |
| 17 | Zhang Zi-ling, Liu Zhi-feng, Cheng Qiang, et al. An approach of comprehensive error modeling and accuracy allocation for the improvement of reliability and optimization of cost of multi-axis NC machine tool[J]. The International Journal of Advanced Manufacturing Technology, 2016, 89(1): 561-579. |
| 18 | 张明. 结构可靠度分析: 方法与程序[M]. 北京: 科学出版社, 2009. |
| 19 | Cheng Qiang, Wu Can, Gu Pei-hua, et al. An analysis methodology for stochastic characteristic of volumetric error in multiaxis CNC machine tool[J]. Mathematical Problems in Engineering, 2013(11): 863283. |
| 20 | Abdul W K. Calibration of 5-axis machine tools[D]. Beijing: School of Mechanical Engineering and Automation, Beihang University, 2010. |
| 21 | 陈传海, 姚国祥, 金桐彤, 等. 基于响应面与遗传算法的主轴系统动力学建模及参数修正[J/OL]. [2021-08-10]. . |
| [1] | 陈传海,王成功,杨兆军,刘志峰,田海龙. 数控机床可靠性建模研究现状及发展动态分析[J]. 吉林大学学报(工学版), 2022, 52(2): 253-266. |
| [2] | 李国龙,陶小会,徐凯,李喆裕. 数控机床转台位置相关几何误差的快速测量与辨识[J]. 吉林大学学报(工学版), 2021, 51(2): 458-467. |
| [3] | 孙晓颖, 扈泽正, 杨锦鹏. 基于分层贝叶斯网络的车辆发动机系统电磁脉冲敏感度评估[J]. 吉林大学学报(工学版), 2018, 48(4): 1254-1264. |
| [4] | 陈东辉, 吕建华, 龙刚, 张宇晨, 常志勇. 基于ADAMS的半悬挂式农业机组静侧翻稳定性[J]. 吉林大学学报(工学版), 2018, 48(4): 1176-1183. |
| [5] | 孙晓颖, 王震, 杨锦鹏, 扈泽正, 陈建. 基于贝叶斯网络的电子节气门电磁敏感度评估[J]. 吉林大学学报(工学版), 2018, 48(1): 281-289. |
| [6] | 李洪洲, 杨兆军, 许彬彬, 王彦鹍, 贾玉辉, 侯超. 数控机床可靠性评估试验周期设计[J]. 吉林大学学报(工学版), 2016, 46(5): 1520-1527. |
| [7] | 高印寒, 安占扬, 王举贤, 王天皓, 刘长英, 张俊东. 等效线束法在汽车线束时域辐射敏感度分析中的应用[J]. 吉林大学学报(工学版), 2015, 45(3): 946-952. |
| [8] | 杨兆军, 杨川贵, 陈菲, 郝庆波, 郑志同, 王松. 基于PSO算法和SVR模型的加工中心可靠性模型参数估计[J]. 吉林大学学报(工学版), 2015, 45(3): 829-836. |
| [9] | 蔡朝晖, 张健沛, 杨静. 基于贝叶斯网络的路网位置匿名区域估计[J]. 吉林大学学报(工学版), 2014, 44(2): 454-458. |
| [10] | 陈传海, 杨兆军, 陈菲, 郝庆波, 许彬彬, 阚英男. 基于Bootstrap-Bayes的加工中心主轴可靠性建模[J]. 吉林大学学报(工学版), 2014, 44(01): 95-100. |
| [11] | 陈传海, 杨兆军, 陈菲, 郝庆波, 许彬彬, 阚英男. 基于模糊数据包络分析的数控机床故障模式分析[J]. 吉林大学学报(工学版), 2013, 43(06): 1523-1528. |
| [12] | 周伟, 赵胜川. 基于Mixed Logit模型的路线选择行为量化分析[J]. 吉林大学学报(工学版), 2013, 43(02): 304-309. |
| [13] | 李小兵, 杨兆军, 李国发, 赵宏伟, 陈菲, 朱晓翠. 基于函数性数据分析的数控机床瞬时可用度建模[J]. , 2012, 42(05): 1151-1156. |
| [14] | 许彬彬, 杨兆军, 陈菲, 郝庆波, 赵宏伟, 李国发. 非齐次泊松过程的数控机床可靠性建模[J]. 吉林大学学报(工学版), 2011, 41(增刊2): 210-214. |
| [15] | 魏领会1,2,申桂香1,张英芝1,陈炳锟1,薛玉霞1. 数控机床可用度建模与仿真[J]. 吉林大学学报(工学版), 2011, 41(4): 993-997. |
|
||