混合可靠性模型参数的核密度和引力搜索估计

doi:10.13229/j.cnki.jdxbgxb20180978

摘要/Abstract

摘要：

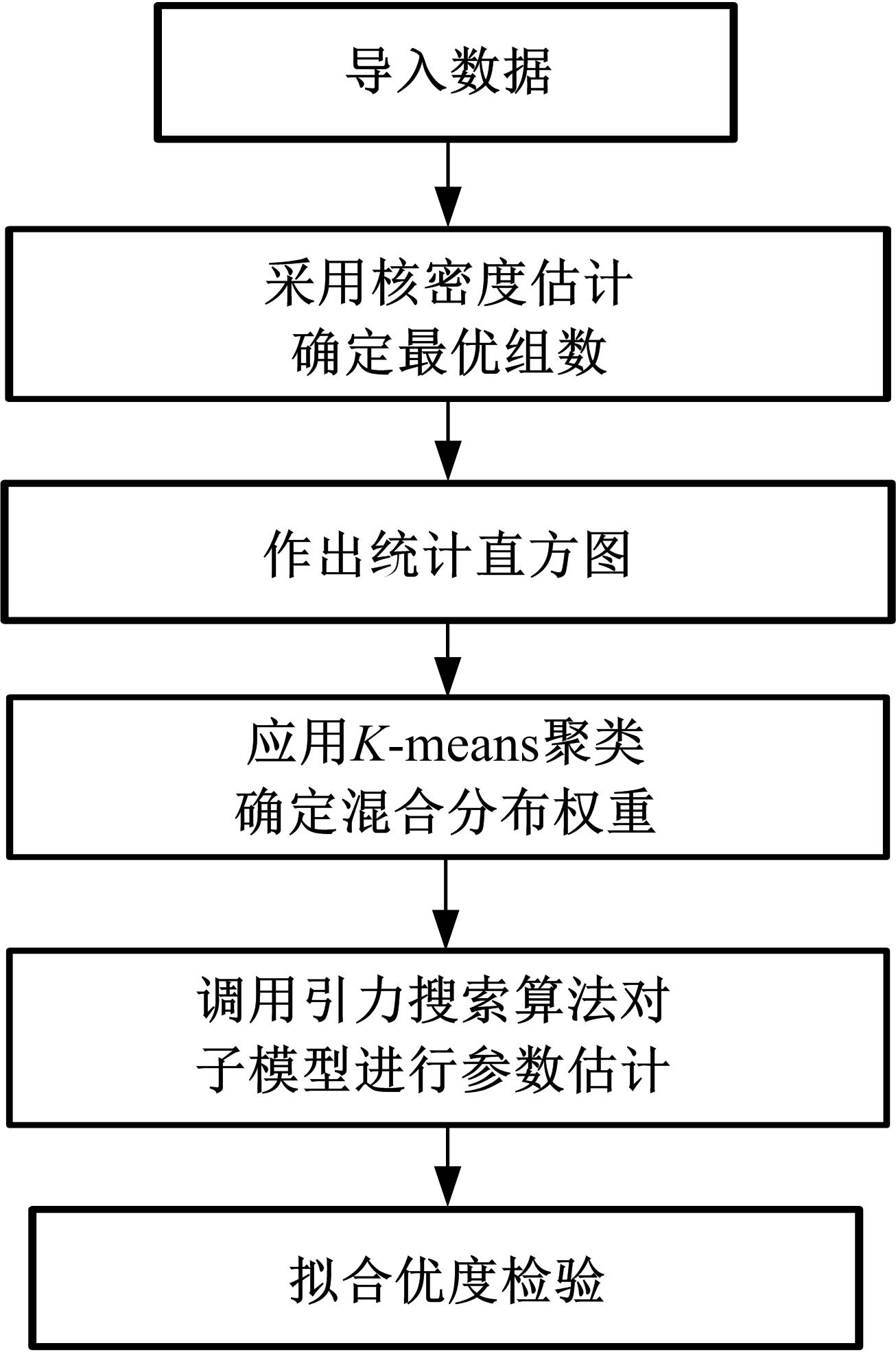
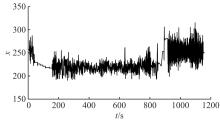
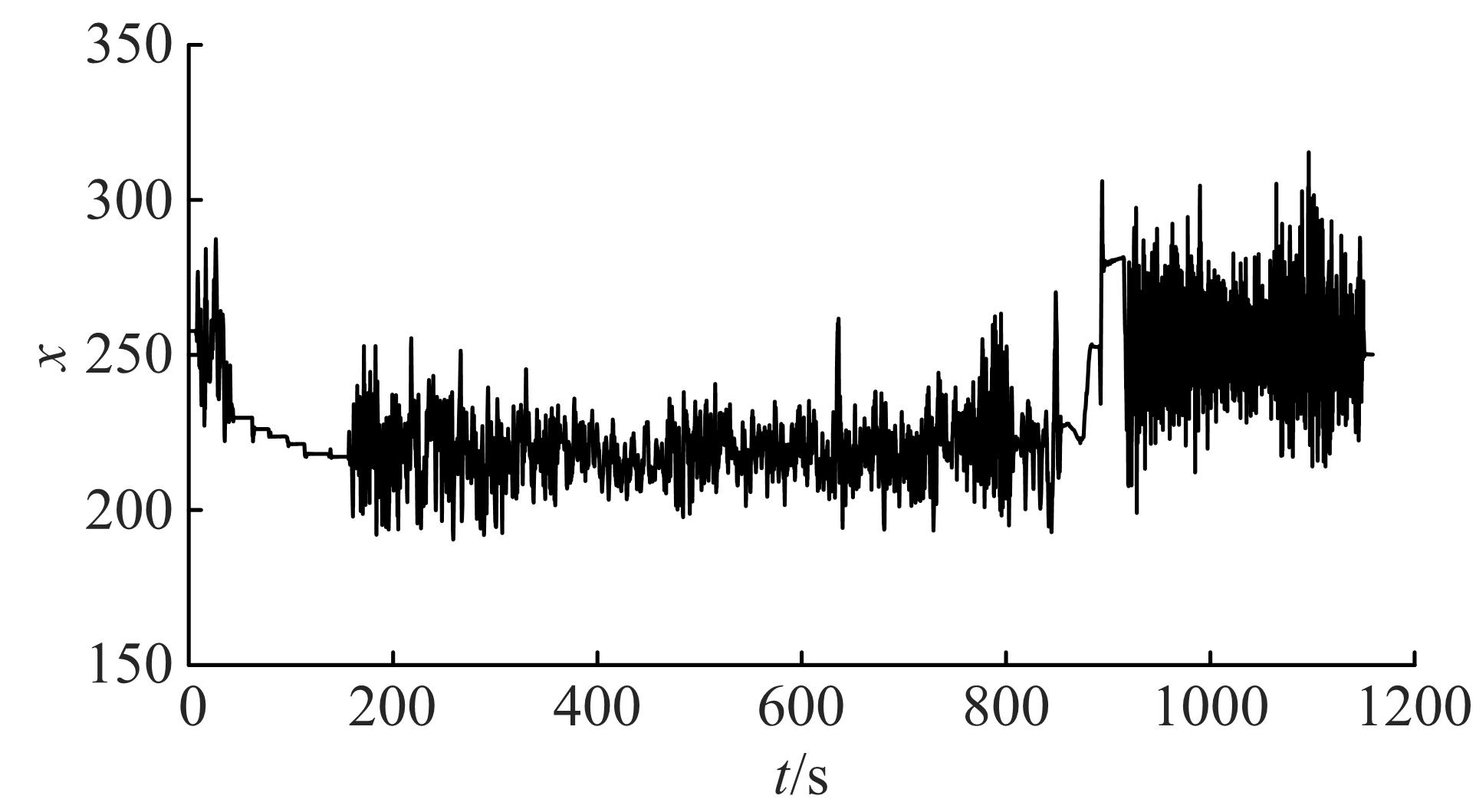
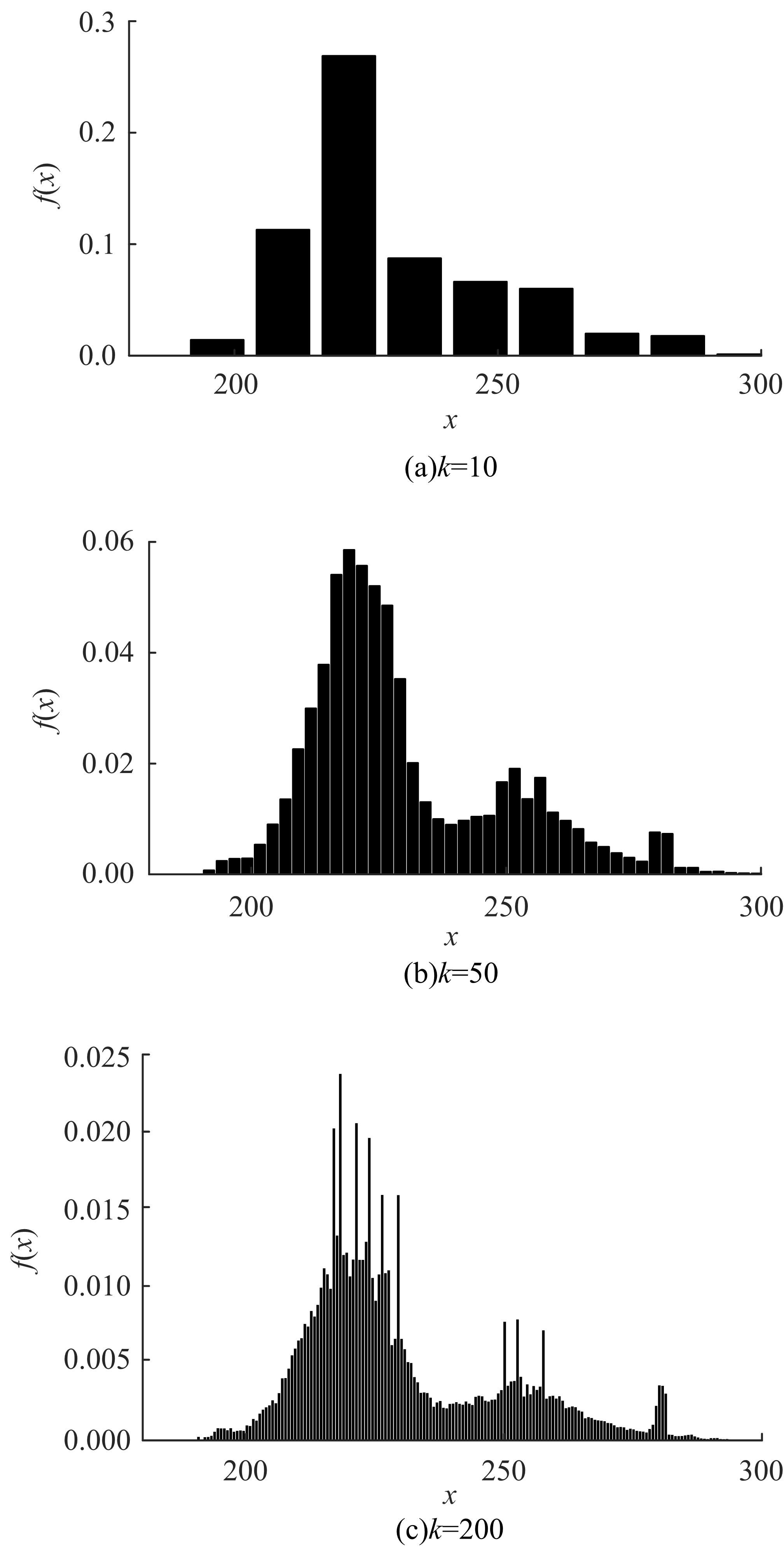
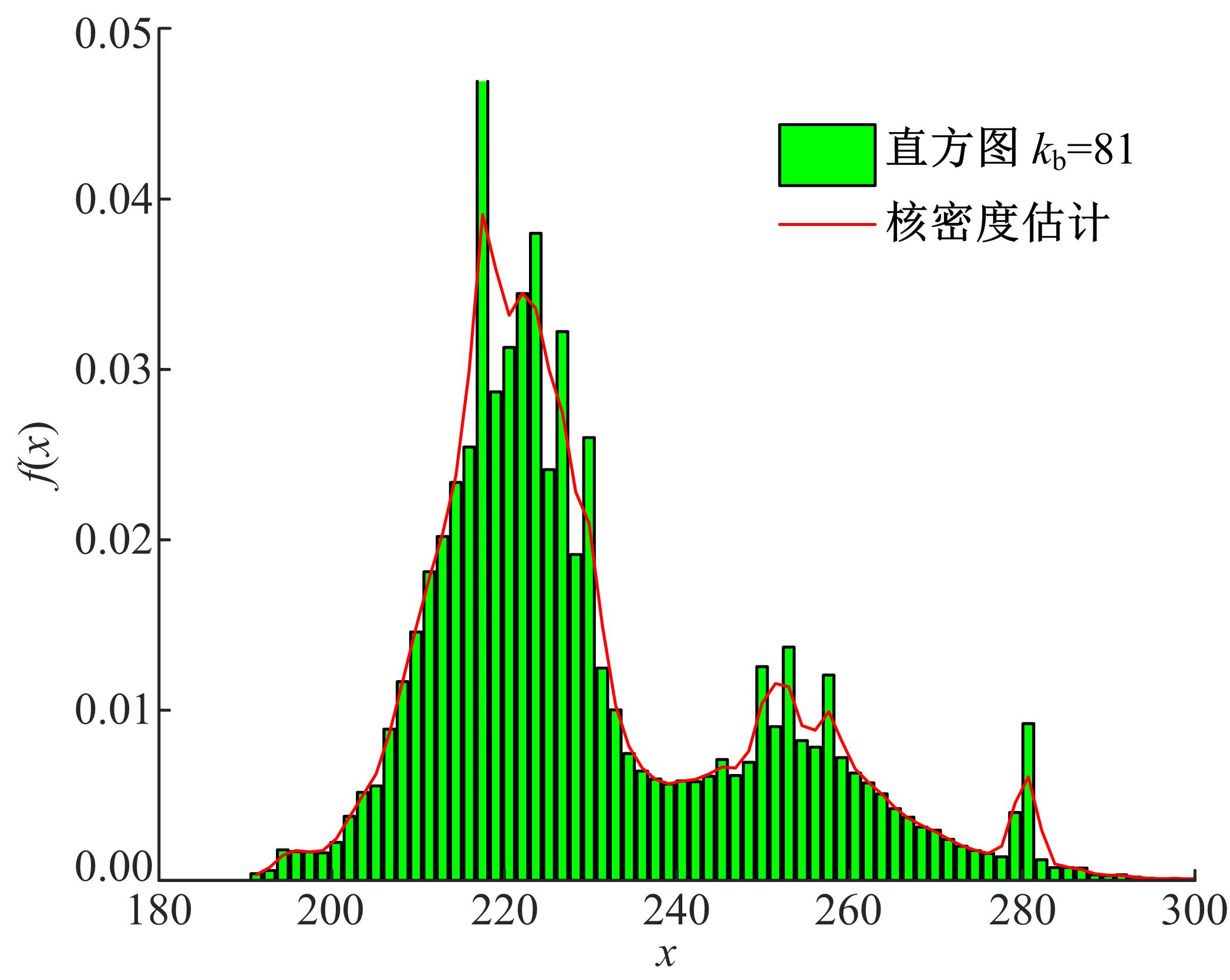
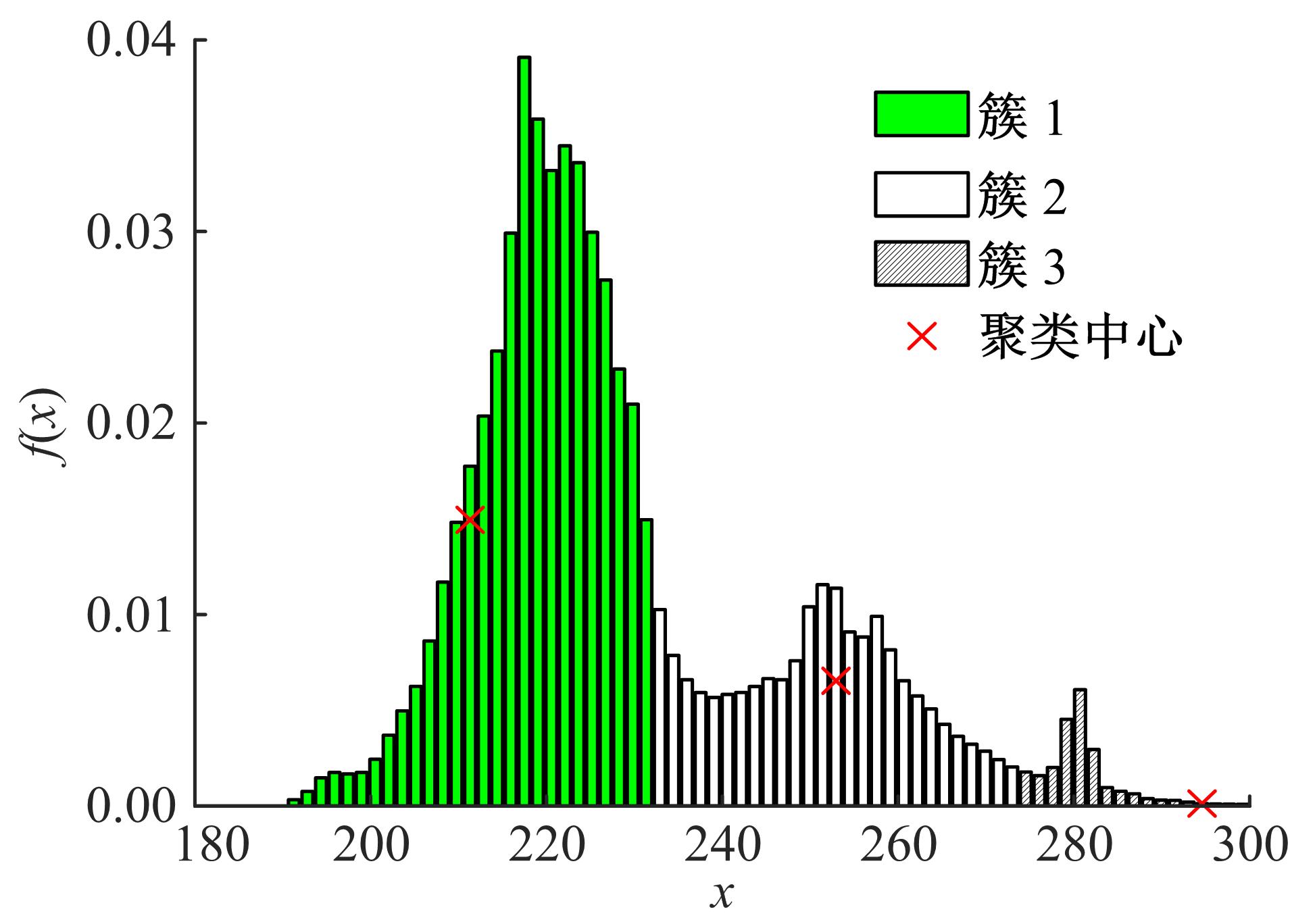
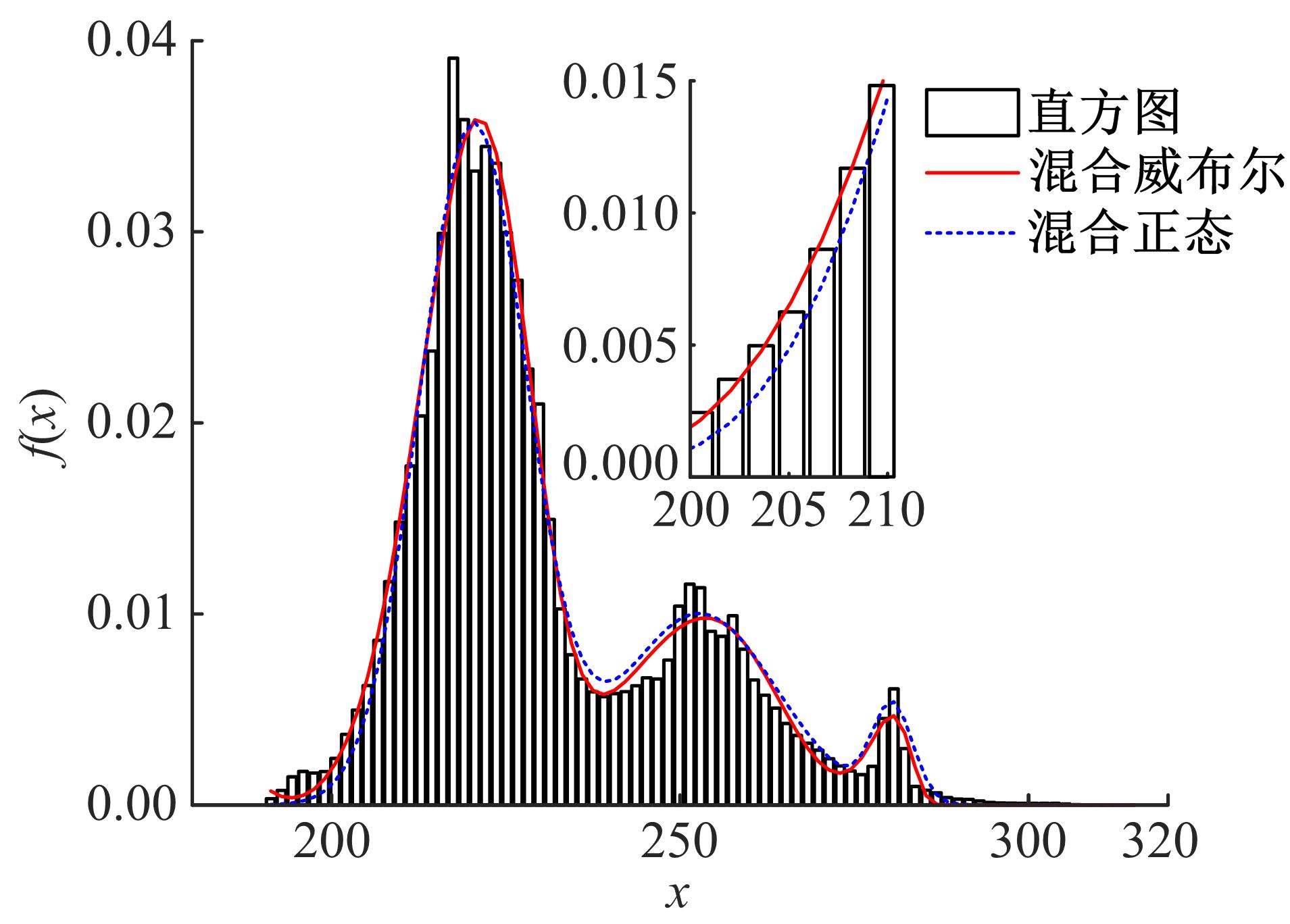
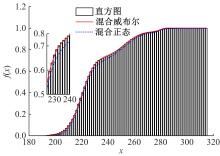
针对可靠性建模中广泛应用的混合分布模型的参数估计问题，为解决其重数选择主观性强、参数识别初值敏感性高、参数识别效率低等难题，融合人工智能方法，提出了一种新型参数估计方法。引入核密度估计对数据进行非参数拟合，以最小化平均积分平方误差为目标，获得核密度估计的最优带宽，以最优带宽为组距对原始数据进行分组，做出统计直方图，并由此确定分布密度函数的混合重数。采用K-均值聚类方法对统计直方图进行聚类，由聚类结果计算获得混合分布模型的权重，接着应用引力搜索算法对混合模型各重子模型的参数进行辨识。以实测商用车车桥位移谱信号为例，对其概率密度函数和累计分布函数进行混合模型建模和模型参数识别。在车桥位移谱模型参数识别的基础上，分别计算决定系数、KS值和平均相对误差3个指标，验证了本文参数估计方法的有效性，为商用车可靠性的疲劳载荷谱编制和实验室台架试验奠定了基础，同时，可以为相关可靠性建模和模型参数识别问题提供参考。

关键词: 车辆工程, 可靠性建模, 参数识别, 核密度, 引力搜索算法, 聚类

Abstract:

To estimate the parameters of the mixed distribution models which are widely used in reliability modeling, a new parameter estimation method was proposed. The kernel density estimation was introduced to non-parametric fitting of the data. With the minimized mean integration square error, the optimal bandwidth of kernel density estimation (KDE) was obtained. The original data were grouped by the optimal bandwidth of KDE as the group distance, and the statistical histogram was made. The mixed multiplicity of the distribution density function was determined by the histogram. The K-means clustering method was employed to cluster the histograms. The weights of the mixed distribution model were calculated from the clustering results. Then the gravitational search algorithm (GSA) was applied to identify the parameters of the sub-distributions' parameters for the mixed model. Taking the measured displacement signal of vehicle axle as an example, mixed reliability model was developed, in which the model parameters were estimated by the proposed method. Based on the identification results of model parameters, the determination coefficient, Kolmogorov-Smirnov coefficient and average relative error were calculated respectively, with which the effectiveness of the proposed parameter estimation method was verified. This research would lay the foundation for the fatigue load spectrum preparation and laboratory reliability bench test of commercial vehicle. Moreover, it can provide reference for related reliability modeling and model parameter identification.

Key words: vehicle engineering, reliability modeling, parameter identification, kernel density estimation, gravitational search algorithm, clustering

中图分类号:

U270.18

刘巧斌,史文库,陈志勇,骆联盟,苏志勇,黄开军. 混合可靠性模型参数的核密度和引力搜索估计[J]. 吉林大学学报(工学版), 2019, 49(6): 1818-1825.

Qiao-bin LIU,Wen-ku SHI,Zhi-yong CHEN,Lian-meng LUO,Zhi-yong SU,Kai-jun HUANG. Parameter estimation of mixed reliability model based on kernel density optimal grouping and gravity search algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(6): 1818-1825.

图/表 10

图1

图2

图3

图4

图5

图6

表1

混合模型参数估计结果"

模型	数值
混合正态分布	$μ 1 = 220.349 ? 1, σ 1 = 7.674 ? 1; μ 2 = 252.801 ? 6, σ 2 = 11.065 ? 5; μ 3 = 280.481 ? 7, σ 3 = 2.899 ? 7$
混合威布尔分布	$α 1 = 34.887 ? 7, β 1 = 4.758 ? 9, γ 1 = 187.728 ? 2; α 2 = 89.960 ? 7, β 2 = 8.551 ? 6, γ 2 = 164.981 ? 8; α 3 = 48.771 ? 8, β 3 = 16.953 ? 6, γ 3 = 231.885 ? 0$

表1

图7

图8

表2

拟合优度结果对比"

指标	混合正态分布	混合威布尔分布
R $2$	0.992 0	0.993 6
D _max	0.034 2	0.010 0
MRE/%	12.91	5.98

表2

参考文献

1	谢里阳 . 可靠性设计[M]. 北京: 高等教育出版社, 2013.
2	Nagode M , Fajdiga M . An improved algorithm for parameter estimation suitable for mixed Weibull distributions[J]. International Journal of Fatigue, 2000, 22(1): 75-80.
3	Krifa M . A mixed Weibull model for size reduction of particulate and fibrous materials[J]. Powder Technology, 2009, 194(3): 233-238.
4	Bu?ar T , Nagode M , Fajdiga M . Reliability approximation using finite Weibull mixture distributions[J]. Reliability Engineering & System Safety, 2004, 84(3): 241-251.
5	蒋仁言 . 威布尔模型族:特性、参数估计和应用[M]. 北京：科学出版社, 1998.
6	Nwobi F N , Ugomma C A . A comparison of methods for the estimation of Weibull distribution parameters[J]. Advances in Methodology & Statistics, 2014, 11(1): 65-78.
7	方开泰, 许建伦 . 统计分布[M]. 北京:高等教育出版社, 2016.
8	Datsiou K C , Overend M . Weibull parameter estimation and goodness-of-fit for glass strength data[J]. Structural Safety, 2018, 73:29-41.
9	Davies I J . Unbiased estimation of the Weibull scale parameter using linear least squares analysis[J]. Journal of the European Ceramic Society, 2017, 37(8): 2973-2981.
10	魏艳华, 王丙参, 邢永忠 . 指数-威布尔分布参数贝叶斯估计的混合Gibbs算法[J]. 统计与决策, 2017(16):70-73.
10	Wei Yan-hua , Wang Bing-shen , Xing Yong-zhong . Mixed gibbs algorithm of Bayesian estimation of parameters for exponentiated Weibull distribution[J]. Statistics and Decision, 2017(16): 70-73.
11	Ignacio M , Chubynsky M V , Slater G W . Interpreting the Weibull fitting parameters for diffusion-controlled release data[J]. Physica A：Statistical Mechanics & Its Applications, 2017, 486：486-496.
12	吴龙涛, 王铁宁, 杨帆 . 基于贝叶斯法和蒙特卡洛仿真的威布尔型装备器材需求预测[J]. 兵工学报, 2017, 38(12): 2447-2454.
12	Wu Long-tao , Wang Tie-ning , Yang Fan . Demand forecasting of equipment and materials by Weibull distribution based on Bayesian estimation and Monte Carlo simulation[J]. Acta Armamentarii, 2017, 38(12): 2447-2454.
13	郑锐 . 三参数威布尔分布参数估计及在可靠性分析中的应用[J]. 振动与冲击, 2015, 34(5):78-81.
13	Zheng Rui . Parameter estimation of three-parameter Weibull distribution and its application in reliability analysis[J]. Journal of Vibration and Shock, 2015, 34(5): 78-81.
14	王晓峰, 张英芝, 申桂香,等 . 基于 ITLS 和 DE 的加工中心三参数威布尔分布[J]. 华南理工大学学报:自然科学版, 2015, 43(6): 84-88.
14	Wang Xiao-feng , Zhang Ying-zhi , Shen Gui-xiang , et al . Three-parameter Weibull distribution of machining center based on ITLS and DE[J]. Journal of South China University of Technology (Natural Science Edition), 2015, 43(6): 84-88.
15	许伟, 程刚, 黄林,等 . 基于混沌模拟退火PSO算法的威布尔分布参数估计应用研究[J]. 振动与冲击, 2017, 36(12): 134-139.
15	Xu Wei , Cheng Gang , Huang Lin , et al . A chaotic simulated PSO algorithm application for Weibull distribution parameter estimation[J]. Journal of Vibration and Shock, 2017, 36(12): 134-139.
16	?rkcü H H , ?zsoy V S , Aksoy E , et al . Estimating the parameters of 3-p, Weibull distribution using particle swarm optimization: a comprehensive experimental comparison[J]. Applied Mathematics & Computation, 2015, 268(9): 201-226.
17	Abbasi B , Niaki S T A , Khalife M A , et al . A hybrid variable neighborhood search and simulated annealing algorithm to estimate the three parameters of the Weibull distribution[J]. Expert Systems with Applications, 2011, 38(1): 700-708.
18	Abbasi B , Hosseinifard S Z , Coit D W . A neural network applied to estimate Burr XII distribution parameters[J]. Reliability Engineering & System Safety, 2010, 95(6): 647-654.
19	Xu M , Droguett E L , Lins I D , et al . On the q-Weibull distribution for reliability applications: an adaptive hybrid artificial bee colony algorithm for parameter estimation[J]. Reliability Engineering & System Safety, 2017, 158: 93-105.
20	Lacour C , Massart P , Rivoirard V . Estimator selection: a new method with applications to kernel density estimation[J]. Sankhya A, 2017, 79(2): 298-335.
21	Xu X , Yan Z , Xu S . Estimating wind speed probability distribution by diffusion-based kernel density method[J]. Electric Power Systems Research, 2015, 121: 28-37.
22	Silverman B W . Density Estimation for Statistics and Data Analysis[M]. London: Chapman & Hall，1986.
23	MacQueen J . Some methods for classification and analysis of multivariate observations[C]∥Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability，California, 1967: 281-297.
24	Rashedi E , Nezamabadi-Pour H , Saryazdi S . GSA: a gravitational search algorithm[J]. Information Sciences, 2009, 179(13): 2232-2248.
25	Li C , Zhou J , Xiao J , et al . Parameters identification of chaotic system by chaotic gravitational search algorithm[J]. Chaos Solitons & Fractals, 2012, 45(4): 539-547.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

[1]	李军军,曹建农,程贝贝,廖娟,朱莹莹. 联合像素与多尺度对象的高分辨率遥感影像谱聚类分割[J]. 吉林大学学报(工学版), 2019, 49(6): 2098-2108.
[2]	陈鑫,阮新建,李铭,王宁,王佳宁,潘凯旋. 基于大涡模拟的离散格式改进方法及应用[J]. 吉林大学学报(工学版), 2019, 49(6): 1756-1763.
[3]	何仁,涂琨. 基于温度补偿气隙宽度的电磁制动器[J]. 吉林大学学报(工学版), 2019, 49(6): 1777-1785.
[4]	靳立强, 田端洋, 田浩, 刘蒙蒙. 汽车电子稳定系统制动增力辅助技术[J]. 吉林大学学报(工学版), 2019, 49(6): 1764-1776.
[5]	李杰, 郭文翠, 赵旗, 谷盛丰. 基于车辆响应的路面不平度识别方法[J]. 吉林大学学报(工学版), 2019, 49(6): 1810-1817.
[6]	管欣,金号,段春光,卢萍萍. 汽车行驶道路侧向坡度估计[J]. 吉林大学学报(工学版), 2019, 49(6): 1802-1809.
[7]	王杨,宋占帅,郭孔辉,庄晔. 转动惯量试验台的惯性参数测量[J]. 吉林大学学报(工学版), 2019, 49(6): 1795-1801.
[8]	庄蔚敏,刘洋,王鹏跃,施宏达,徐纪栓. 钢铝异质自冲铆接头剥离失效仿真[J]. 吉林大学学报(工学版), 2019, 49(6): 1826-1835.
[9]	陈百超,邹猛,党兆龙,黄晗,贾阳,石睿杨,李建桥. CE-3月球车筛网轮月面沉陷行为试验[J]. 吉林大学学报(工学版), 2019, 49(6): 1836-1843.
[10]	马芳武,倪利伟,吴量,聂家弘,徐广健. 轮腿式全地形移动机器人位姿闭环控制[J]. 吉林大学学报(工学版), 2019, 49(6): 1745-1755.
[11]	马芳武,韩露,周阳,王世英,蒲永锋. 采用聚乳酸复合材料的汽车零件多材料优化设计[J]. 吉林大学学报(工学版), 2019, 49(5): 1385-1391.
[12]	高振海,孙天骏,何磊. 汽车纵向自动驾驶的因果推理型决策[J]. 吉林大学学报(工学版), 2019, 49(5): 1392-1404.
[13]	张博,张建伟,郭孔辉,丁海涛,褚洪庆. 路感模拟用永磁同步电机电流控制[J]. 吉林大学学报(工学版), 2019, 49(5): 1405-1413.
[14]	王鹏宇,赵世杰,马天飞,熊晓勇,程馨. 基于联合概率数据关联的车用多传感器目标跟踪融合算法[J]. 吉林大学学报(工学版), 2019, 49(5): 1420-1427.
[15]	胡兴军,惠政,郭鹏,张扬辉,张靖龙,王靖宇,刘飞. 基于流固耦合的汽车气动特性[J]. 吉林大学学报(工学版), 2019, 49(5): 1414-1419.