斜拉索悬链线构形的伸长量解析计算方法

doi:10.13229/j.cnki.jdxbgxb20190867

摘要/Abstract

摘要：

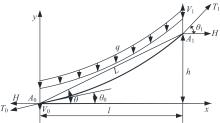
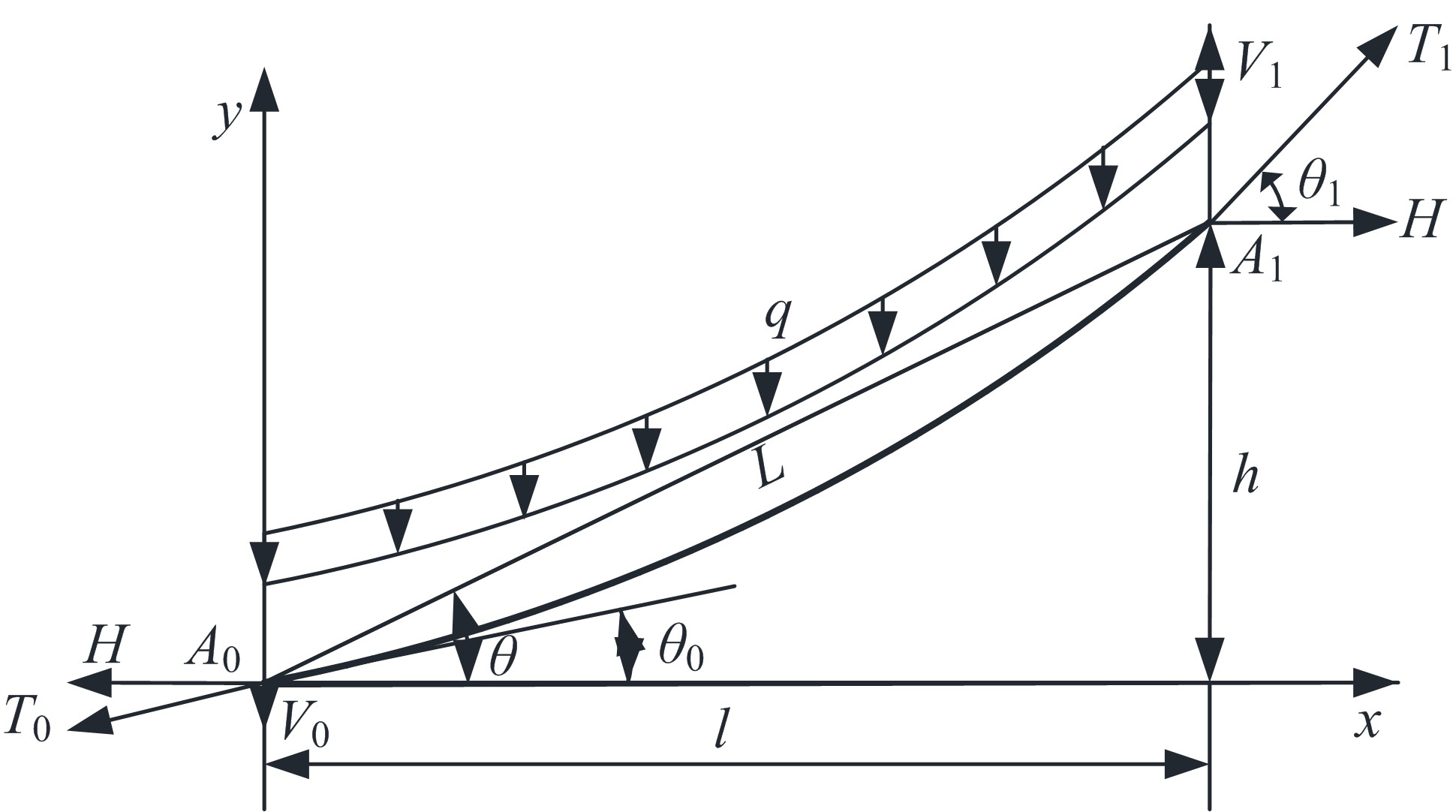
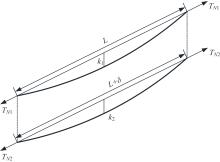
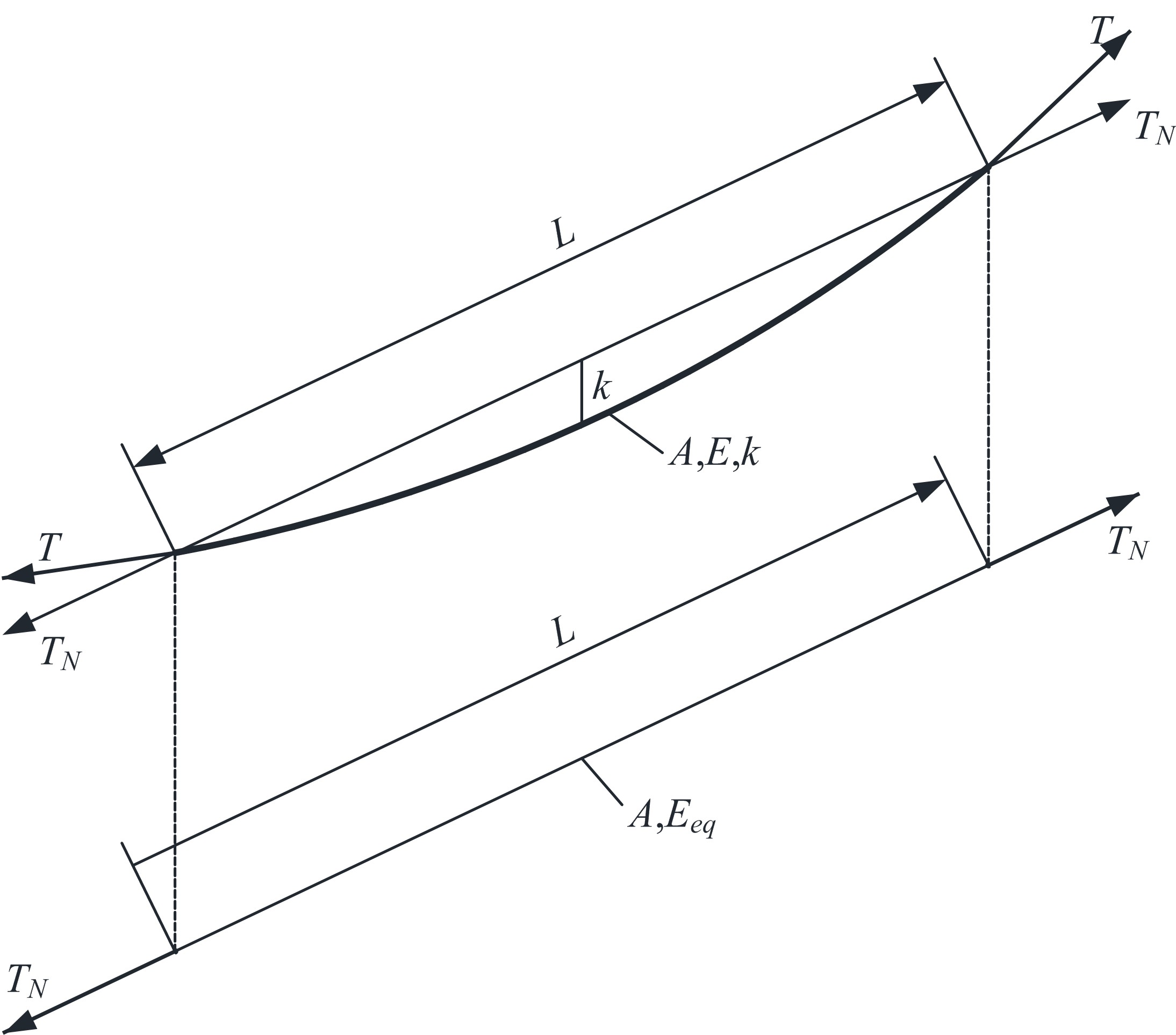
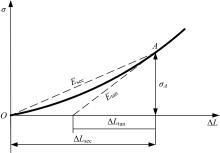
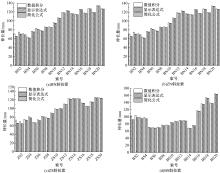
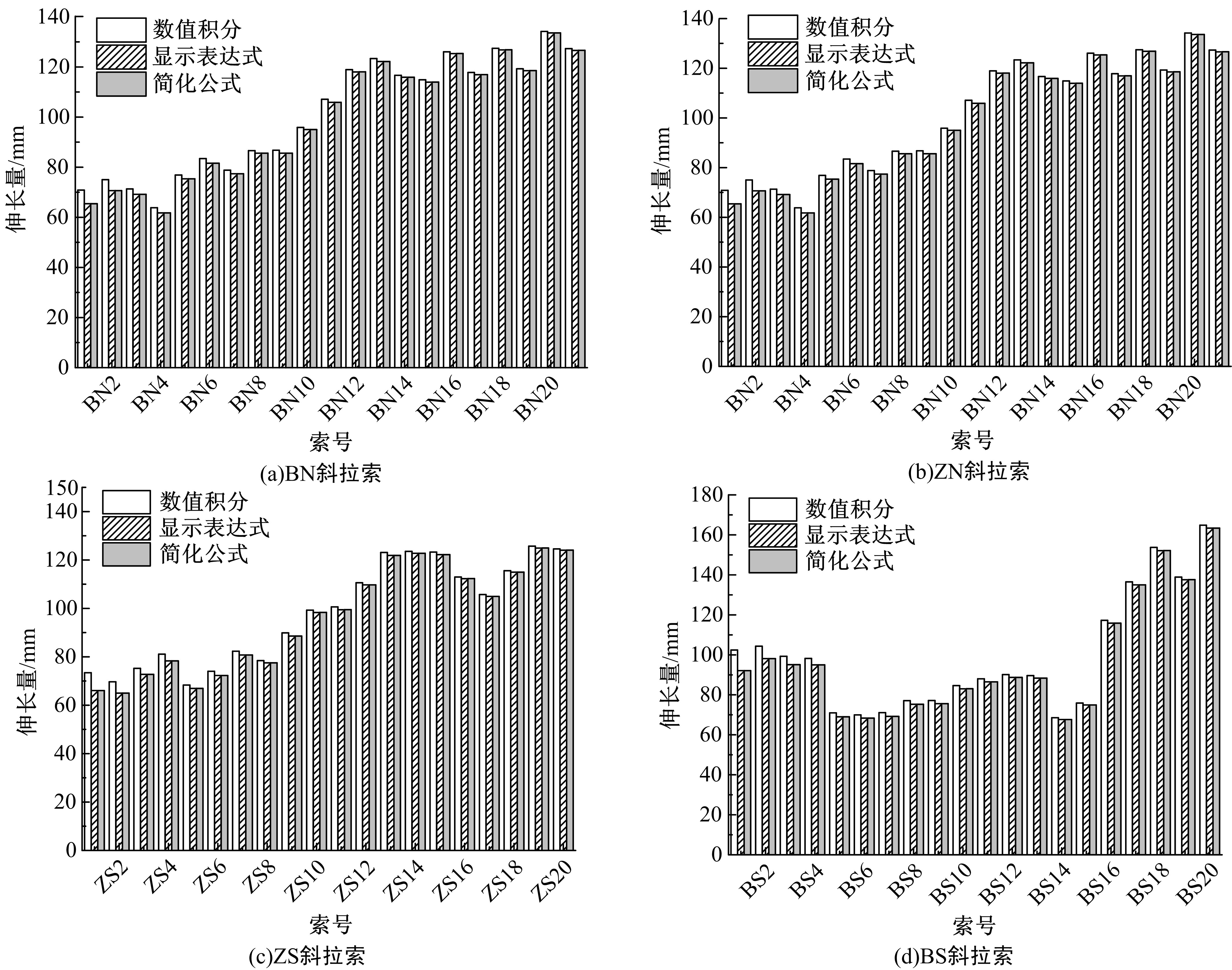
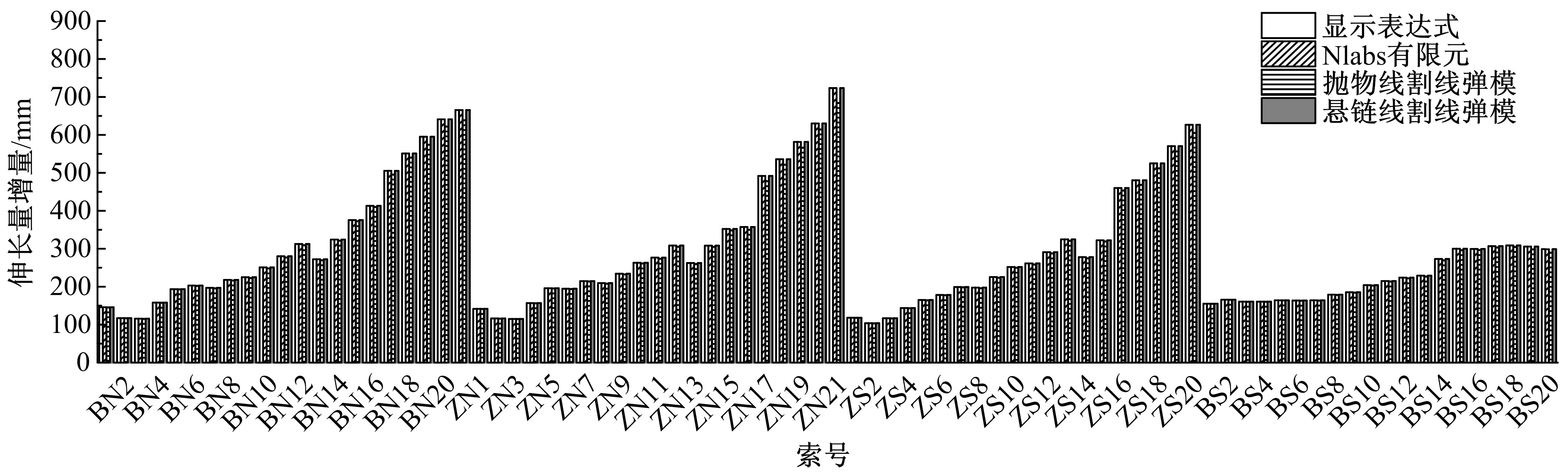
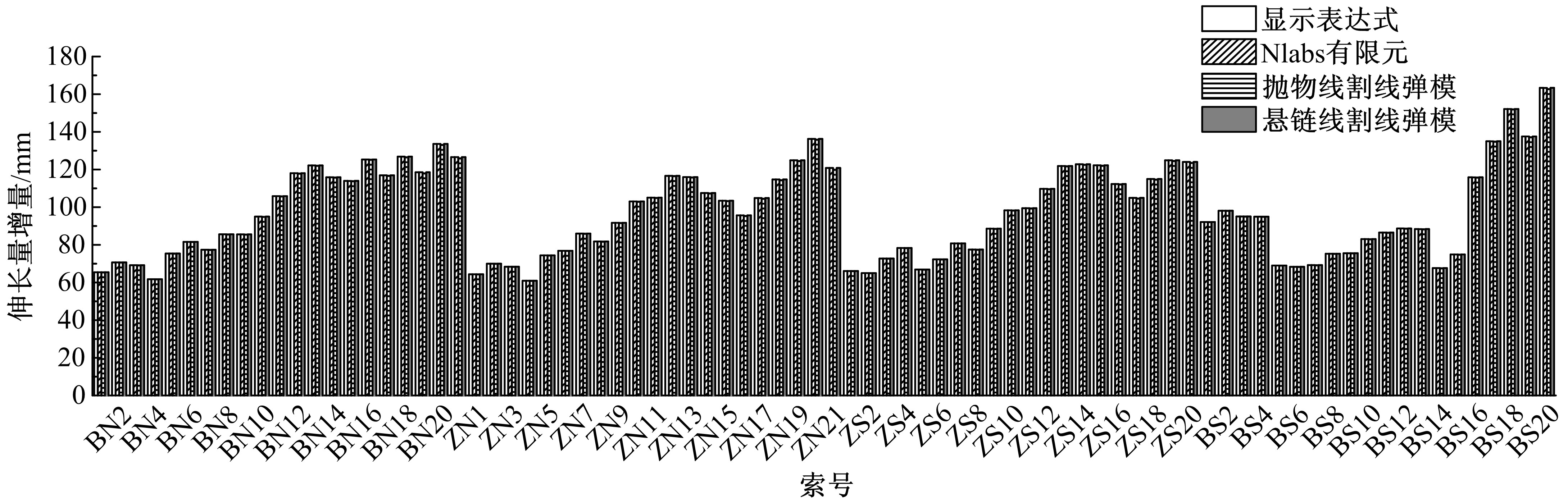
针对斜拉索无应力索长和张拉时伸长量控制的需求，讨论了斜拉索悬链线构形的伸长量解析计算方法。采用斜拉索的力平衡条件，获得悬链线构形的几何方程，进而通过直接积分得到给定索力时索长和伸长量计算的解析表达；利用增量索力作用时的变形协调条件，获得增量索力作用下的伸长量解析表达。基于应变等效，讨论了基于悬链线构形的弹性模量等效，明确了基于悬链线构形的等效弹性模量可以弱化为基于抛物线构形的等效弹性模量。用某叠合/混合梁斜拉桥的实际斜拉索参数，分别用数值积分、简化公式，验证了给定索力时索长和伸长量解析表达式；用Nlabs有限元、等效弹性模量方法验证了增量索力作用下伸长量计算的解析表达式。研究表明：所提解析表达式能简单直接得到精确的斜拉索伸长量，为斜拉索无应力长度和斜拉索安装时的伸长量控制提供了理论和快捷方法。

关键词: 土木工程, 斜拉索, 悬链线构形, 伸长量, 抛物线构形

Abstract:

In order to meet the requirements of unstressed length and elongation control for stay cable during its installation， the analytical method for calculating the elongation of the stay cable with catenary configuration is discussed. First， the geometric equation of the stay cable with catenary configuration is obtained by applying the force equilibrium condition to the stay cable， and the analytical expressions of the cable length and its elongation under a certain given cable tension are acquired by direct integration. Moreover， the analytical expressions of the cable elongation under varying cable tension are obtained by using the deformation coordination condition. Then， the equivalent elastic modulus for stay cable with catenary configuration is discussed based on strain equivalence. It is verified that the equivalent elastic modulus for the stay cable with catenary configuration can be simplified to the equivalent elastic modulus for the stay cable with parabolic configuration. Taking the real parameters of the stay cables of a certain cable-stayed bridge with composite/hybrid girder as the case study， the analytical expressions of stay cable length and its corresponding elongation under a given cable tension are verified by numerical integration and simplified formulas respectively. Furthermore， the analytical expressions for the elongation of stay cable with varying cable tension are verified by the Nlabs finite element and equivalent elastic modulus method. The results show that the proposed analytical expressions can simply and directly figure out the exact elongation of stay cable， which provide the theory and straight forward method for the unstressed length of stay cable and the elongation control of stay cable during its installation.

Key words: civil engineering, stay cable, catenary configuration, elongation, parabolic configuration

中图分类号:

U448

单德山,张潇,顾晓宇,李乔. 斜拉索悬链线构形的伸长量解析计算方法[J]. 吉林大学学报(工学版), 2021, 51(1): 217-224.

De-shan SHAN,Xiao ZHANG,Xiao-yu GU,Qiao LI. Analytical method for elongation of stayed-cable with catenary configuration[J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(1): 217-224.

图/表 9

图1

图2

图3

图 4

图 5

表1

图 6

图 7

图 8

参考文献 18

1	Li H, Zhang F, Jin Y. Real-time identification of time-varying tension in stay cables by monitoring cable transversal acceleration[J]. Structural Control and Health Monitoring, 2014, 21(7): 1100-1117.
2	An Y, Zhong Y, Tan Y, et al. Experimental and numerical studies on a test method for damage diagnosis of stay cables[J]. Advances in Structural Engineering, 2017, 20(2): 245-256.
3	Gimsing N J, Georgakis C T. Cable Supported Bridges-Concept and Design[M]. 3rd ed. Chichester, West Sussex, United Kingdom: John Wiley & Sons Ltd, 2012.
4	李乔, 卜一之, 张清华. 大跨度斜拉桥施工全过程几何控制概论与应用[M]. 成都:西南交通大学出版社, 2009.
5	Wu J, Frangopol D M, Soliman M. Geometry control simulation for long-span steel cable-stayed bridges based on geometrically nonlinear analysis[J]. Engineering Structures, 2015, 90: 71-82.
6	Ernst H J. The E-Module of rope with consideration of the dip[J]. The Civil Engineering, 1965, 40(1): 52-55.
7	Hajdin N, Michaltsos G T, Konstantakopoulos T G. About the equivalent modulus of elasticity of cables of cable-stayed bridges[J]. The Scientific Journal Facta Universitatis, 1998, 11(5): 569-575.
8	郝超, 裴岷山, 强士中. 大跨度斜拉桥拉索无应力长度的计算方法比较[J]. 重庆交通学院学报, 2001, 20(3): 1-3.
	Hao Chao, Pei Min-shan, Qiang Shi-zhong. Comparison of algorithm for calculating non-stress length of cable in long-span cable-stayed bridges[J]. Journal of Chongqing Jiaotong University, 2001, 20(3): 1-3.
9	任淑琰, 顾明. 斜拉桥拉索静力构形分析[J]. 同济大学学报:自然科学版, 2005, 33(5): 595-599.
	Ren Shu-yan, Gu Ming. Static analysis of cables' configuration in cable-Stayed bridges[J]. Journal of Tongji University(Natural Science Edition), 2005, 33(5): 595-599.
10	杨佑发, 白文轩, 郜建人. 悬链线解答在斜拉索数值分析的应用[J]. 重庆建筑大学学报, 2007, 29(6): 31-34.
	Yang You-fa, Bai Wen-xuan, Gao Jian-ren. Application of Catenary Solution in numerical analysis of stay cables[J]. Journal of Chongqing University of Architecture, 2007, 29(6): 31-34.
11	李乔, 周凌远. 桥梁结构非线性分析系统NLABS使用说明书[M]. 成都:西南交通大学出版社, 2019.
12	Wu Z, Wei J. Nonlinear analysis of spatial cable of long-span cable-stayed bridge considering rigid connection[J]. KSCE Journal of Civil Engineering, 2019, 23(5): 2148-2157.
13	梁鹏, 肖汝诚, 孙斌. 超大跨度斜拉桥几何非线性精细化分析[J]. 中国公路学报, 2007, 20(2): 57-62.
	Liang Peng, Xiao Ru-cheng, Sun Bin. Refined geometrical nonlinear analysis for super-long-span cable-stayed bridge[J]. China Journal of Highway and Transport, 2007, 20(2): 57-62.
14	汪峰, 刘沐宇. 斜拉桥无应力索长的精确求解方法[J]. 华中科技大学学报:自然科学版, 2010, 38(7): 54-57.
	Wang Feng, Liu Mu-yu. An accurate method for determining unstressed cable length in long span cable stayed bridge[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2010, 38(7): 54-57.
15	苑仁安, 秦顺全. 无应力状态法在钢绞线斜拉索施工中的应用[J]. 桥梁建设, 2012, 42(3): 75-79.
	Yuan Ren-an, Qin Shun-quan. Application of unstressed state method to construction of steel strand stay cable[J]. Bridge Construction, 2012, 42(3): 75-79.
16	Kumarasena S, Jones N P, Irwin P, et al. Wind-induced vibration of stay cables[R]. Washington DC:United States Department of Transportation, 2007: 213-217.
17	孟庆成, 齐欣, 李乔, 等. 千米级斜拉桥斜拉索相关参数计算方法[J]. 桥梁建设, 2009(2): 58-60, 75.
	Meng Qing-cheng, Qi Xin, Li Qiao, et al. Algorithm for relevant parameters of stay cables of cable-stayed bridge with span length of 1 000-m scale[J]. Bridge Construction, 2009(2): 58-60, 75.
18	Vairo G. A closed-form refined model of the cables' nonlinear response in cable-stayed structures[J]. Mechanics of Advanced Materials and Structures, 2009, 16(6): 456-466.

相关文章 15

[1]	薛素铎,鲁建,李雄彦,刘人杰. 跳格布置对环形交叉索桁结构静动力性能的影响[J]. 吉林大学学报(工学版), 2020, 50(5): 1687-1697.
[2]	王勃,董元正,董丽欣. 基于短期风速资料的基本风压计算方法[J]. 吉林大学学报(工学版), 2020, 50(5): 1739-1746.
[3]	李明,王浩然,赵唯坚. 单向带抗剪键叠合板的受力性能试验[J]. 吉林大学学报(工学版), 2020, 50(2): 654-667.
[4]	王鹏辉,乔宏霞,冯琼,曹辉,温少勇. 氯氧镁涂层钢筋混凝土两重因素耦合作用下的耐久性模型[J]. 吉林大学学报(工学版), 2020, 50(1): 191-201.
[5]	李明,王浩然,赵唯坚. 带抗剪键叠合板的力学性能[J]. 吉林大学学报(工学版), 2019, 49(5): 1509-1520.
[6]	张军,钱诚,郭春燕,钱玉君. 基于多源时空数据的建筑宜居性动态设计[J]. 吉林大学学报(工学版), 2019, 49(4): 1169-1173.
[7]	梁宁慧,缪庆旭,刘新荣,代继飞,钟祖良. 聚丙烯纤维增强混凝土断裂韧度及软化本构曲线确定[J]. 吉林大学学报(工学版), 2019, 49(4): 1144-1152.
[8]	张磊,刘保国,储昭飞. 深厚孔隙砂岩含水层疏干排水对盾构斜井的影响模型试验[J]. 吉林大学学报(工学版), 2019, 49(3): 788-797.
[9]	郑一峰, 赵群, 暴伟, 李壮, 于笑非. 大跨径刚构连续梁桥悬臂施工阶段抗风性能[J]. 吉林大学学报(工学版), 2018, 48(2): 466-472.
[10]	王腾, 周茗如, 马连生, 乔宏霞. 基于断裂理论的湿陷性黄土劈裂注浆裂纹扩展[J]. 吉林大学学报(工学版), 2017, 47(5): 1472-1481.
[11]	郭楠, 张平阳, 左煜, 左宏亮. 竹板增强胶合木梁受弯性能[J]. 吉林大学学报(工学版), 2017, 47(3): 778-788.
[12]	张静, 刘向东. 混沌粒子群算法优化最小二乘支持向量机的混凝土强度预测[J]. 吉林大学学报(工学版), 2016, 46(4): 1097-1102.
[13]	郭学东, 马立军, 张云龙. 集中力作用下考虑剪切滑移效应的双层结合面组合梁解析解[J]. 吉林大学学报(工学版), 2016, 46(2): 432-438.
[14]	赵玉，李衍赫，张培，赵科，刘伟超. 粘土的动力特性试验[J]. 吉林大学学报(工学版), 2015, 45(6): 1791-1797.
[15]	侯忠明, 王元清, 夏禾, 张天申. 移动荷载作用下的钢-混简支结合梁动力响应[J]. 吉林大学学报(工学版), 2015, 45(5): 1420-1427.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

索号	钢束规格	索长/m	索号	钢束规格	索长/m
ZN1	M250?43	95.218	BN1	M250?43	95.740
ZN2	M250?37	102.747	BN2	M250?37	103.637
ZN3	M250?37	110.259	BN3	M250?37	111.484
ZN4	M250?37	118.312	BN4	M250?37	119.840
ZN5	M250?43	126.783	BN5	M250?43	128.574
ZN6	M250?43	135.787	BN6	M250?43	137.801
ZN7	M250?43	146.672	BN7	M250?50	148.888
ZN8	M250?50	157.413	BN8	M250?50	159.813
ZN9	M250?50	168.569	BN9	M250?55	171.135
ZN10	M250?50	180.101	BN10	M250?55	182.817
ZN11	M250?55	191.881	BN11	M250?55	194.731
ZN12	M250?61	203.900	BN12	M250?55	206.865
ZN13	M250?61	216.121	BN13	M250?61	219.185
ZN14	M250?61	228.512	BN14	M250?61	231.650
ZN15	M250?73	241.047	BN15	M250?61	244.267
ZN16	M250?73	253.706	BN16	M250?61	256.987
ZN17	M250?73	266.474	BN17	M250?73	269.806
ZN18	M250?73	279.331	BN18	M250?73	282.707
ZN19	M250?73	292.271	BN19	M250?85	296.683
ZN20	M250?73	305.283	BN20	M250?85	308.723
ZN21	M250?85	318.358	BN21	M250?85	313.023
ZS1	M250?37	91.274	BS1	M250?55	96.099
ZS2	M250?37	99.436	BS2	M250?55	103.565
ZS3	M250?37	107.445	BS3	M250?55	110.055
ZS4	M250?37	115.793	BS4	M250?55	116.216
ZS5	M250?43	124.395	BS5	M250?61	122.024
ZS6	M250?43	133.479	BS6	M250?61	127.999
ZS7	M250?43	144.144	BS7	M250?61	135.001
ZS8	M250?50	154.718	BS8	M250?61	141.864
ZS9	M250-50	165.734	BS9	M250?73	149.004
ZS10	M250?50	177.157	BS10	M250?73	156.412
ZS11	M250?55	188.836	BS11	M250?73	164.000
ZS12	M250?55	200.770	BS12	M250?73	171.770
ZS13	M250?55	212.918	BS13	M250?73	179.732
ZS14	M250?61	225.246	BS14	M250?73	187.799
ZS15	M250?61	237.727	BS15	M250?73	196.987
ZS16	M250?61	250.338	BS16	M250?73	204.283
ZS17	M250?73	263.062	BS17	M250?73	212.623
ZS18	M250?73	275.885	BS18	M250?73	221.184
ZS19	M250?73	288.792	BS19	M250?85	229.732
ZS20	M250?73	301.775	BS20	M250?85	238.348