吉林大学学报(工学版) ›› 2025, Vol. 55 ›› Issue (3): 1093-1102.doi: 10.13229/j.cnki.jdxbgxb.20230578

• 通信与控制工程 • 上一篇    

Alpha稳定分布噪声下基于近似l0范数稀疏重构的波达方向估计

单泽彪1,2,3(),薛泓垚1,刘小松1(),姚瑞广1,陈广秋1   

  1. 1.长春理工大学 电子信息工程学院，长春 130022
    2.吉林大学 通信工程学院，长春 130022
    3.长春气象仪器研究所，长春 130012
  • 收稿日期:2023-06-08 出版日期:2025-03-01 发布日期:2025-05-20
  • 通讯作者: 刘小松 E-mail:zbshan@126.com;liuxs@cust.edu.cn
  • 作者简介:单泽彪（1986-），男，副教授，博士.研究方向：阵列信号处理，压缩感知技术.E-mail：zbshan@126.com
  • 基金资助:
    吉林省自然科学基金项目(20250102050JC)

Direction of arrival estimation based on approximate l0 norm sparse reconstruction under Alpha stable distribution noise

Ze-biao SHAN1,2,3(),Hong-yao XUE1,Xiao-song LIU1(),Rui-guang YAO1,Guang-qiu CHEN1   

  1. 1.School of Electronic and Information Engineering，Changchun University of Science and Technology，Changchun 130022，China
    2.College of Communication Engineering，Jilin University，Changchun 130022，China
    3.Changchun Meteorological Instrument Research Institute，Changchun 130012，China
  • Received:2023-06-08 Online:2025-03-01 Published:2025-05-20
  • Contact: Xiao-song LIU E-mail:zbshan@126.com;liuxs@cust.edu.cn

RICH HTML

 1   

PDF (PC)

22

摘要：

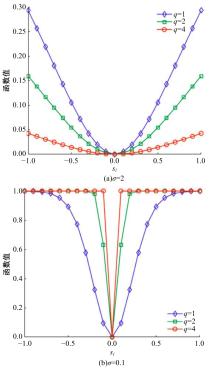
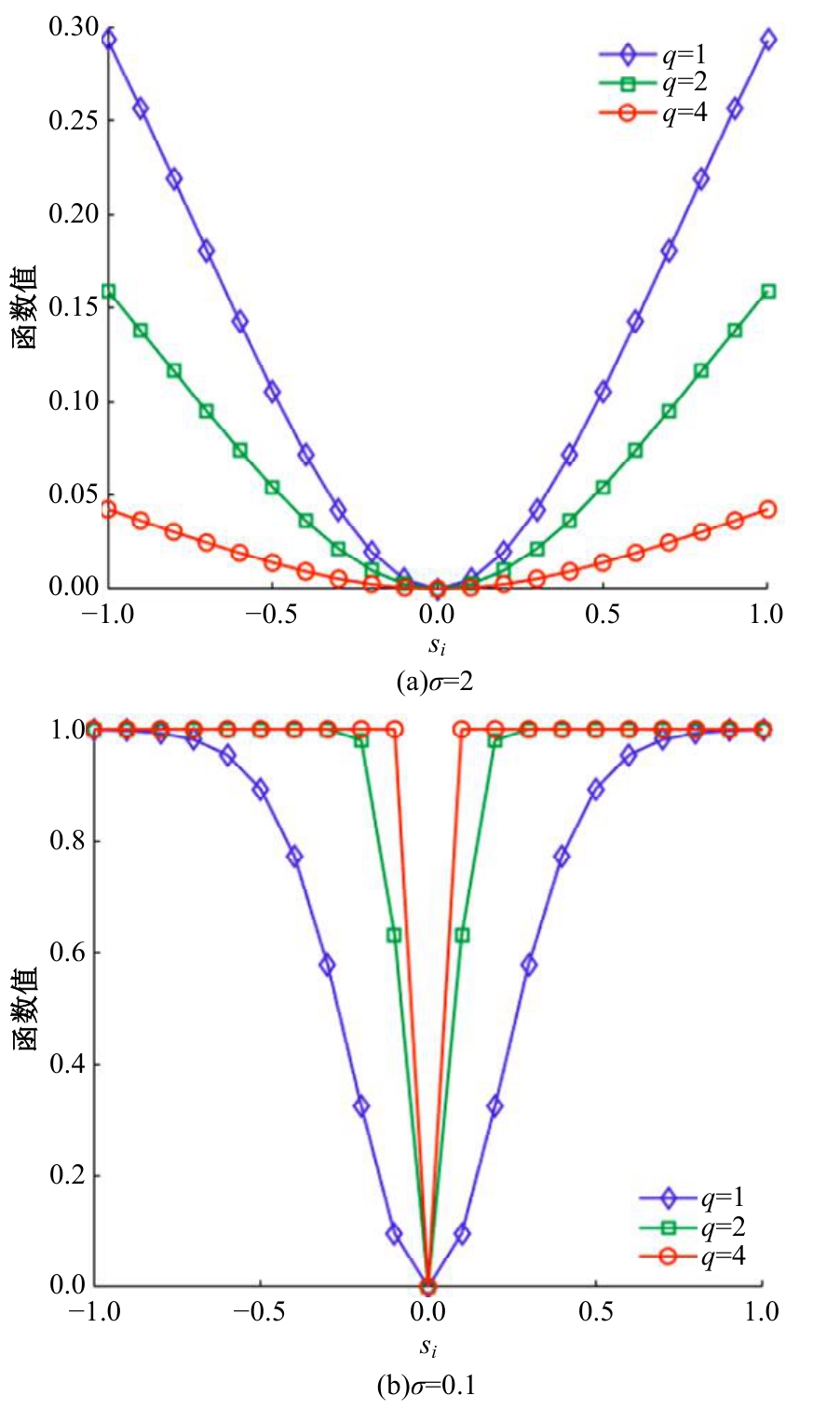
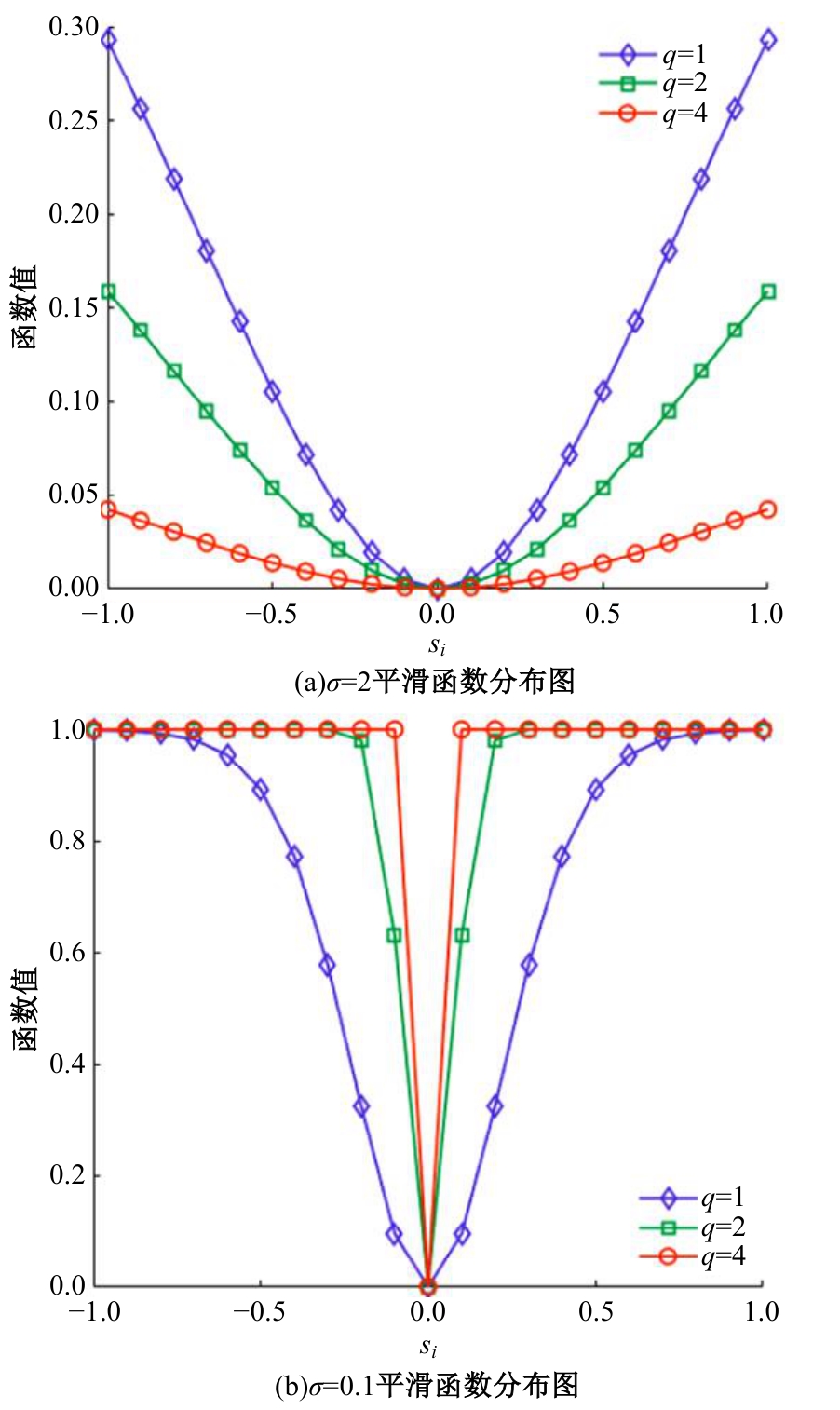
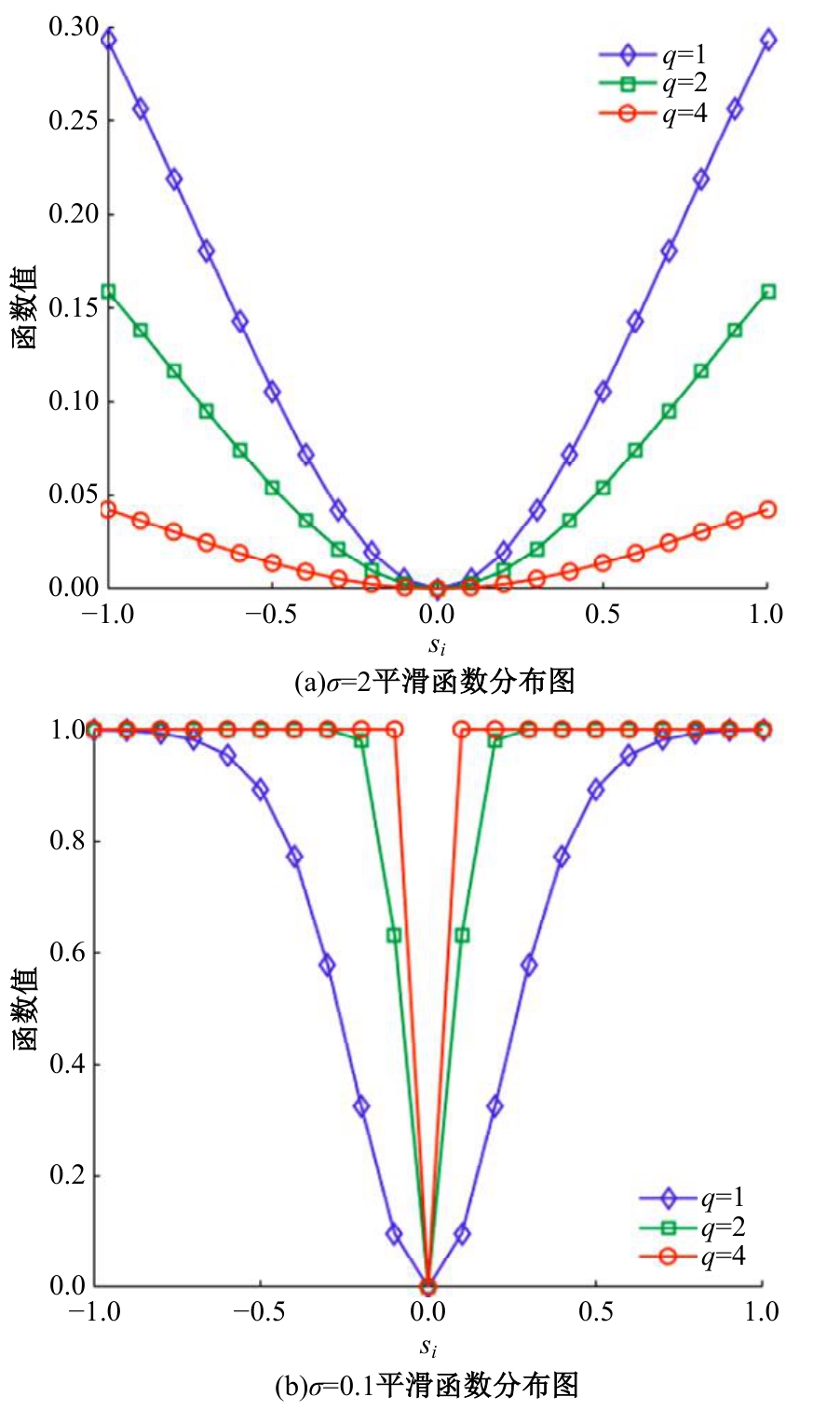
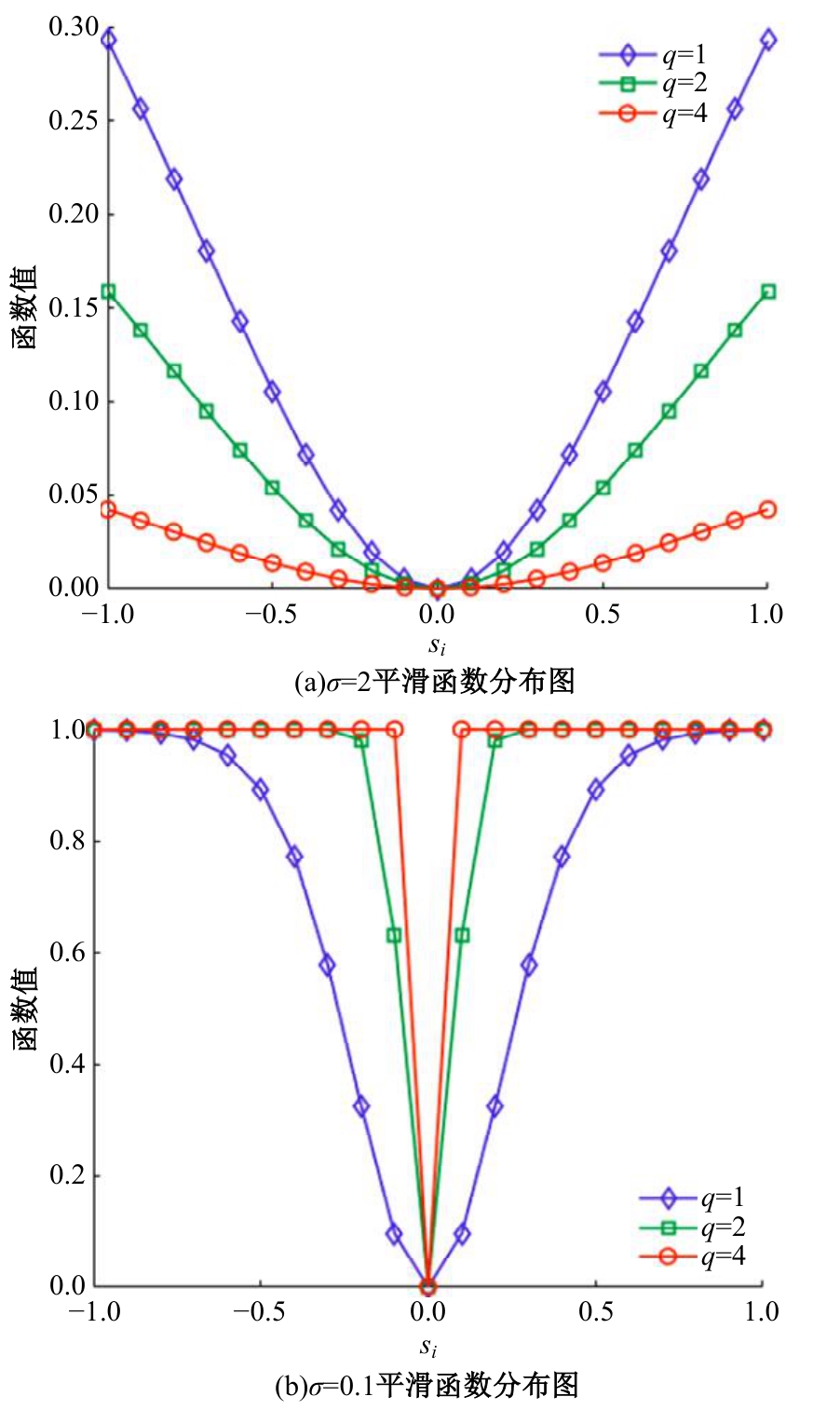
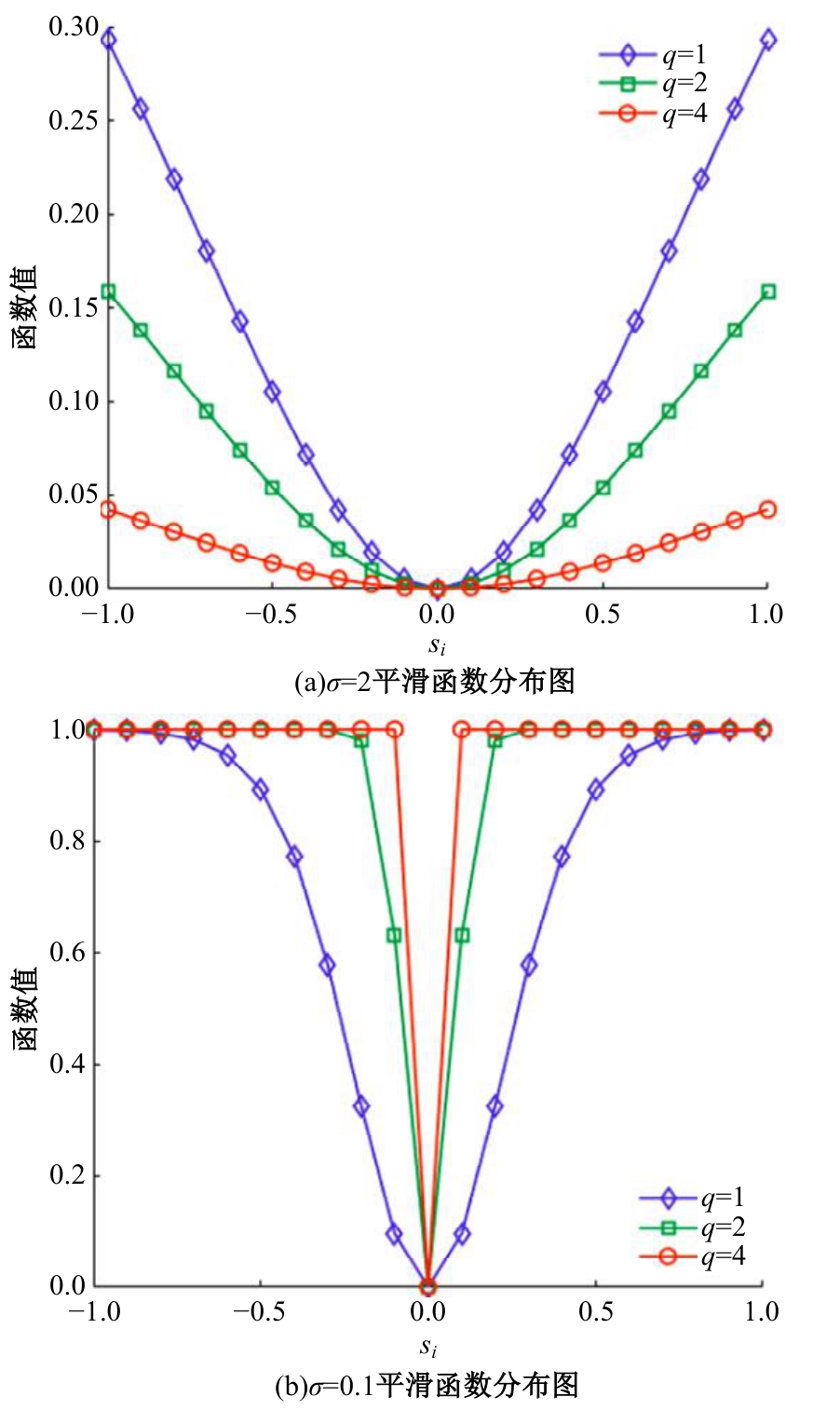
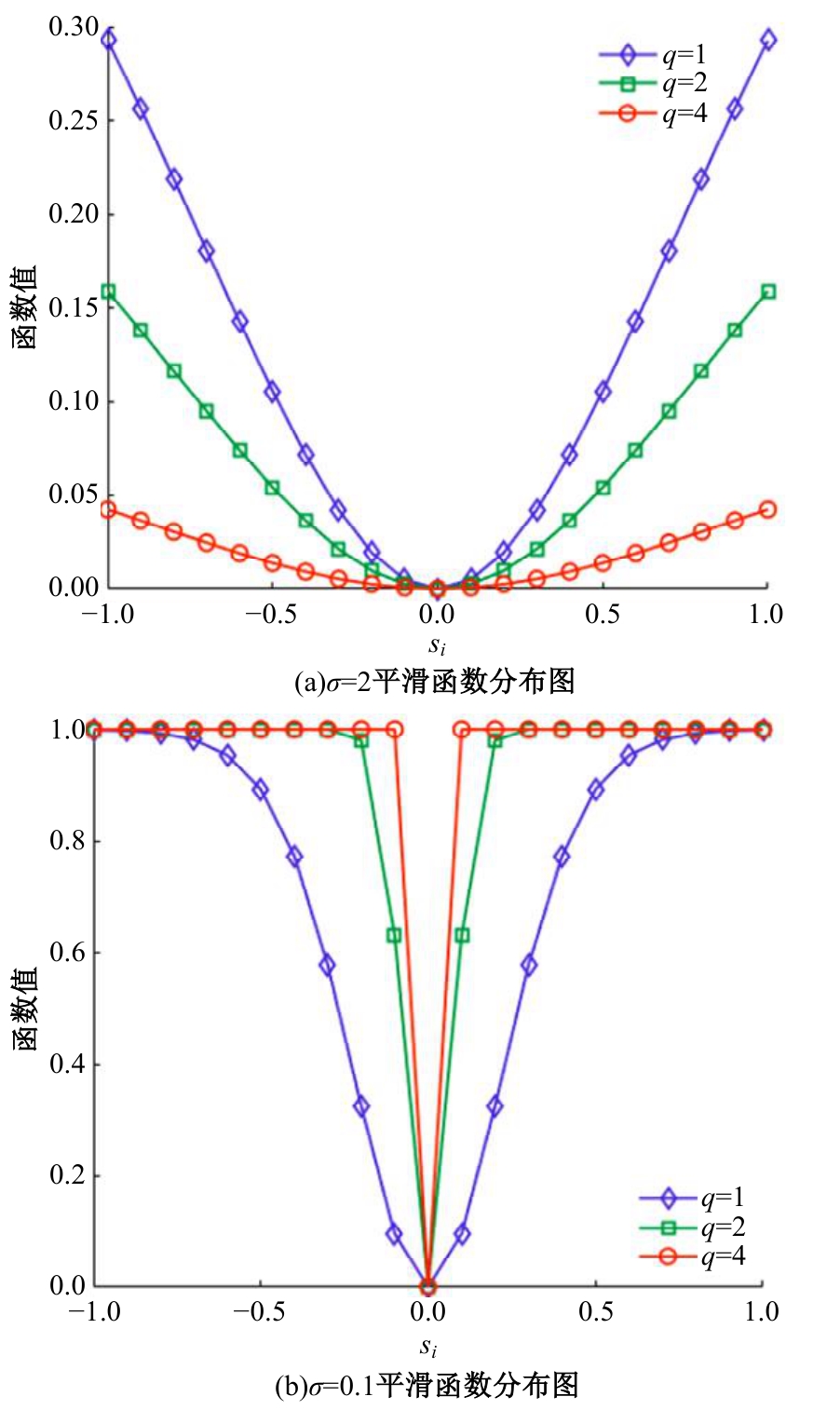
针对Alpha稳定分布噪声背景下基于压缩感知的波达方向（DOA）估计方法在低信噪比、小快拍数条件下估计性能较差的问题，提出了一种基于近似l0范数稀疏重构的DOA估计算法。首先利用分数低阶统计量结合KR子空间法，重塑分数低阶矩矩阵抑制Alpha稳定分布噪声，构造稀疏测向模型。然后通过指数族分布函数分析其平滑性和陡峭性，构造最优的平滑函数近似l0范数求解稀疏测向模型。同时针对离格效应造成的算法误差，将偏移量引入在格稀疏测向模型，对导向矢量矩阵进行一阶泰勒级数展开，建立离格稀疏测向模型，并利用交替迭代法计算信号分量和偏移量，进而得到离格DOA估计值。最后，通过仿真实验验证了本文算法在Alpha稳定分布噪声背景下DOA估计的有效性和优越性。

关键词: 信息处理技术, 波达方向估计, 稀疏重构, Alpha稳定分布, 近似l0范数

Abstract:

Aiming at the problem of poor estimation performance of the compression-aware DOA estimation method based on compression in the context of Alpha stable distribution noise under the conditions of low signal-to-noise ratio and small number of fast beats， a DOA estimation algorithm based on approximate l0 norm sparse reconstruction is proposed. The fractional low-order statistic combined with KR subspace method is used to reshape the fractional low-order moment matrix to suppress the Alpha stable distribution noises and construct the sparse measurement direction model. The smoothness and steepness of the function are analyzed by the exponential family distribution function， and a optimal smoothing function approximating the l0 norm is constructed to solve the sparse measured direction model. For the algorithm error caused by the off-grid effect， the offset is introduced into the in-grid sparse vectorization model， and the first-order Taylor series expansion is performed on the guide vector matrix to establish the off-grid sparse vectorization model. The algorithm uses the alternating iteration method to calculate the signal components and offsets to obtain the off-grid target DOA estimates. The effectiveness and superiority of the proposed algorithm for direction angle estimation in the background of Alpha stable distribution noise is verified by simulation experiments.

Key words: information processing techniques, direction of arrival estimation, sparse reconstruction, Alpha stable distribution, approximate l0 norm

中图分类号: 

  • TN911

图1

平滑函数分布图"

表1

算法计算复杂度对比"

算法复杂度
ESL0O(min(M2,Q))+O(5K)
EOGSL0O(min(M2,Q))+O(7K)
R-OMPO(Q(2M)2)+O(Q)
R-OGOMPO(Q(2M)2)+O(Q)+O(4K)

表2

不同算法原理及特性对比分析"

不同算法算法原理特性适用场景
ESLO近似l0范数计算复杂度低，估计精度高在格
EOGSL0近似l0范数+最小二乘交替迭代计算复杂度低，估计精度高离格
R-OMP正交匹配追踪计算复杂度高，估计精度低在格
R-OGOMP正交匹配追踪+最小二乘交替迭代计算复杂度高，估计精度低离格

图2

不同平滑函数对信号恢复效果图"

图 3

三信源DOA估计结果"

图4

均方根误差随信噪比变化趋势图"

图5

均方根误差随快拍数变化趋势图"

图6

均方根误差随特征指数变化趋势图"

1 Donoho D. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.
2 Candes E J, Romberg J K, Tao T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathematics, 2006, 59(8): 1207-1223.
3 单泽彪, 刘小松, 史红伟, 等. 动态压缩感知波达方向跟踪算法[J]. 吉林大学学报: 工学版, 2018, 48(6): 1938-1944.
Shan Ze-biao, Liu Xiao-song, Shi Hong-wei, et al. DOA tracking algorithm using dynamic compressed sensing[J]. Journal of Jilin University(Engineering and Technology Edition), 2018, 48(6): 1938-1944.
4 单泽彪, 常立民, 刘小松, 等. 基于自然对数复合函数近似l0范数的DOA估计[J].兵工学报, 2023, 44(5): 1521-1528.
Shan Ze-biao, Chang Li-min, Liu Xiao-song, et al. DOA estimation based on approximate l0 norm of natural logarithm composite function[J]. Acta Armamentarii,2023, 44(5): 1521-1528.
5 Cui W, Shen Q, Liu W, et al. Low complexity DOA estimation for wideband off-grid sources based on re-focused compressive sensing with dynamic dictionary[J]. IEEE Journal of Selected Topics in Signal Processing, 2019, 13(5): 918-930.
6 Wu X, Zhu W, Yan J. Direction of arrival estimation for off-grid signals based on sparse Bayesian learning[J]. IEEE Sensors Journal, 2016, 16(7): 2004-2016.
7 Ma Y, Cao X, Wang X. Multi-source off-grid DOA estimation using iterative phase offset correction in coarray domain[J]. Digital Signal Processing, 2021, 112: No.102998.
8 Zhu H, Leus G, Giannakis G B. Sparsity-cognizant total least-squares for perturbed compressive sampling[J]. IEEE Transactions on Signal Processing, 2011, 59(5): 2002-2016.
9 Tan Z, Yang P, Nehorai A. Joint sparse recovery method for compressed sensing with structured dictionary mismatches[J]. IEEE Transactions on Singal Processing, 2014, 62(19): 4997-5008.
10 Yang Z, Zhang C, Xie L. Robustly stable signal recovery in compressed sensing with structures matrix perturbation[J]. IEEE Transactions on Signal Processing, 2012, 60(9): 4658-4671.
11 Li S, Lin B. On spatial smoothing for direction-of-arrival estimation of coherent signals in impulsive noise[C]∥IEEE Advanced Information Technology, Electronic & Automation Control Conference, Chongqing, China, 2015: 806 - 811.
12 Liang L, Shi Y, Shi Y, et al. Direction of arrival estimation with off-grid target based on sparse reconstruction in impulsive noise[J]. Journal of Low Frequency Noise, Vibration and Active Control, 2021, 40(1): 315-331.
13 Liu T H, Mendel J M. A subspace-based direction finding algorithm using fractional lower order statistics[J]. IEEE Transactions on Signal Processing, 2001, 49(8): 1605-1613.
14 Li S, He R, Lin B, et al. DOA estimation based on sparse representation of the fractional lower order statistics in impulsive noise[J]. IEEE/CAA Journal of Automatica Sinica, 2018, 5(4): 860-868.
15 Ma W K, Hsieh T H, Chi C Y. DOA estimation of quasi-stationary signals with less sensors than sources and unknown spatial noise covariance: a Khatri-Rao subspace approach[J]. IEEE Transactions on Signal Processing, 2010, 58: 2168-2180.
[1] 段锦,姚安妮,王震,于林韬. 改进的麻雀搜索算法优化无线传感器网络覆盖[J]. 吉林大学学报(工学版), 2024, 54(3): 761-770.
[2] 肖剑,刘经纬,胡欣,齐小刚. 基于改进非洲秃鹫算法的TDOA-AOA定位[J]. 吉林大学学报(工学版), 2024, 54(12): 3558-3567.
[3] 窦慧晶,谢东旭,郭威,邢路阳. 基于改进的正交匹配跟踪算法的波达方向估计[J]. 吉林大学学报(工学版), 2024, 54(12): 3568-3576.
[4] 苏育挺,王骥,赵玮,井佩光. 基于动态图卷积的图像情感分布预测[J]. 吉林大学学报(工学版), 2023, 53(9): 2601-2610.
[5] 陈绵书,于录录,李晓妮,郑宏宇. 基于均匀ORB特征的回环检测算法[J]. 吉林大学学报(工学版), 2023, 53(9): 2666-2675.
[6] 国强,朱国会,李万臣. 基于混沌麻雀搜索算法的TDOA/FDOA定位[J]. 吉林大学学报(工学版), 2023, 53(2): 593-600.
[7] 徐丽琴,李勇,刘有耀,张建国. 多输入多输出雷达波束空间ESPRIT角度估计方法[J]. 吉林大学学报(工学版), 2022, 52(6): 1459-1465.
[8] 刘洲洲,张倩昀,马新华,彭寒. 基于优化离散差分进化算法的压缩感知信号重构[J]. 吉林大学学报(工学版), 2021, 51(6): 2246-2252.
[9] 窦慧晶,丁钢,高佳,梁霄. 基于压缩感知理论的宽带信号波达方向估计[J]. 吉林大学学报(工学版), 2021, 51(6): 2237-2245.
[10] 王德兴,吴若有,袁红春,宫鹏,王越. 基于多尺度注意力融合和卷积神经网络的水下图像恢复[J]. 吉林大学学报(工学版), 2021, 51(4): 1396-1404.
[11] 李厚杰,王法胜,贺建军,周瑜,李威,窦宇轩. 基于伪样本正则化Faster R⁃CNN的交通标志检测[J]. 吉林大学学报(工学版), 2021, 51(4): 1251-1260.
[12] 蒋华伟,杨震,张鑫,董前林. 图像去雾算法研究进展[J]. 吉林大学学报(工学版), 2021, 51(4): 1169-1181.
[13] 金静,党建武,王阳萍,申东. 融合模糊统计纹理特征的多线索粒子滤波跟踪[J]. 吉林大学学报(工学版), 2021, 51(3): 1111-1120.
[14] 郭继昌,乔珊珊. 基于深度图的水下图像复原[J]. 吉林大学学报(工学版), 2021, 51(2): 677-684.
[15] 刘国华,周文斌. 基于卷积神经网络的脉搏波时频域特征混叠分类[J]. 吉林大学学报(工学版), 2020, 50(5): 1818-1825.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
版权所有 © 《吉林大学学报(工学版)》编辑部
地址：长春市人民大街5988号　电话：+86-431-85095297　传真：+86-431-85094074　E-mail: xbgxb@jlu.edu.cn
本系统由北京玛格泰克科技发展有限公司设计开发