吉林大学学报(工学版) ›› 2022, Vol. 52 ›› Issue (6): 1394-1403.doi: 10.13229/j.cnki.jdxbgxb20210013
• 交通运输工程·土木工程 • 上一篇
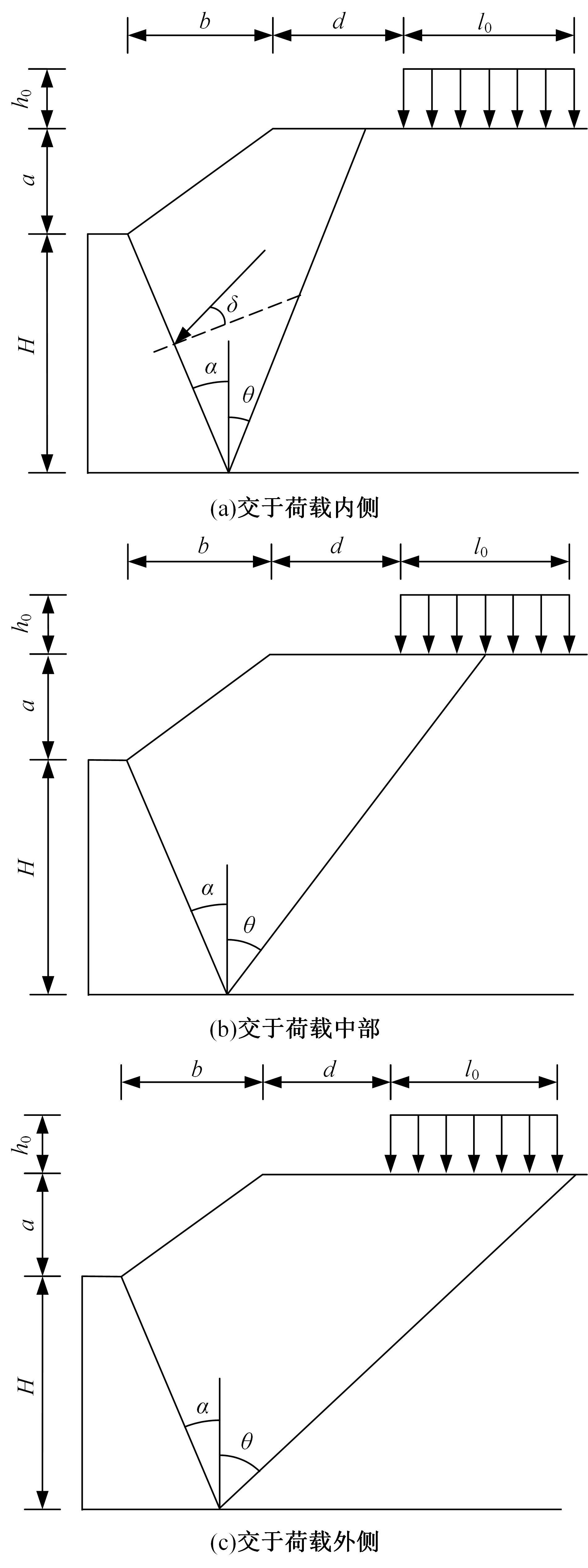
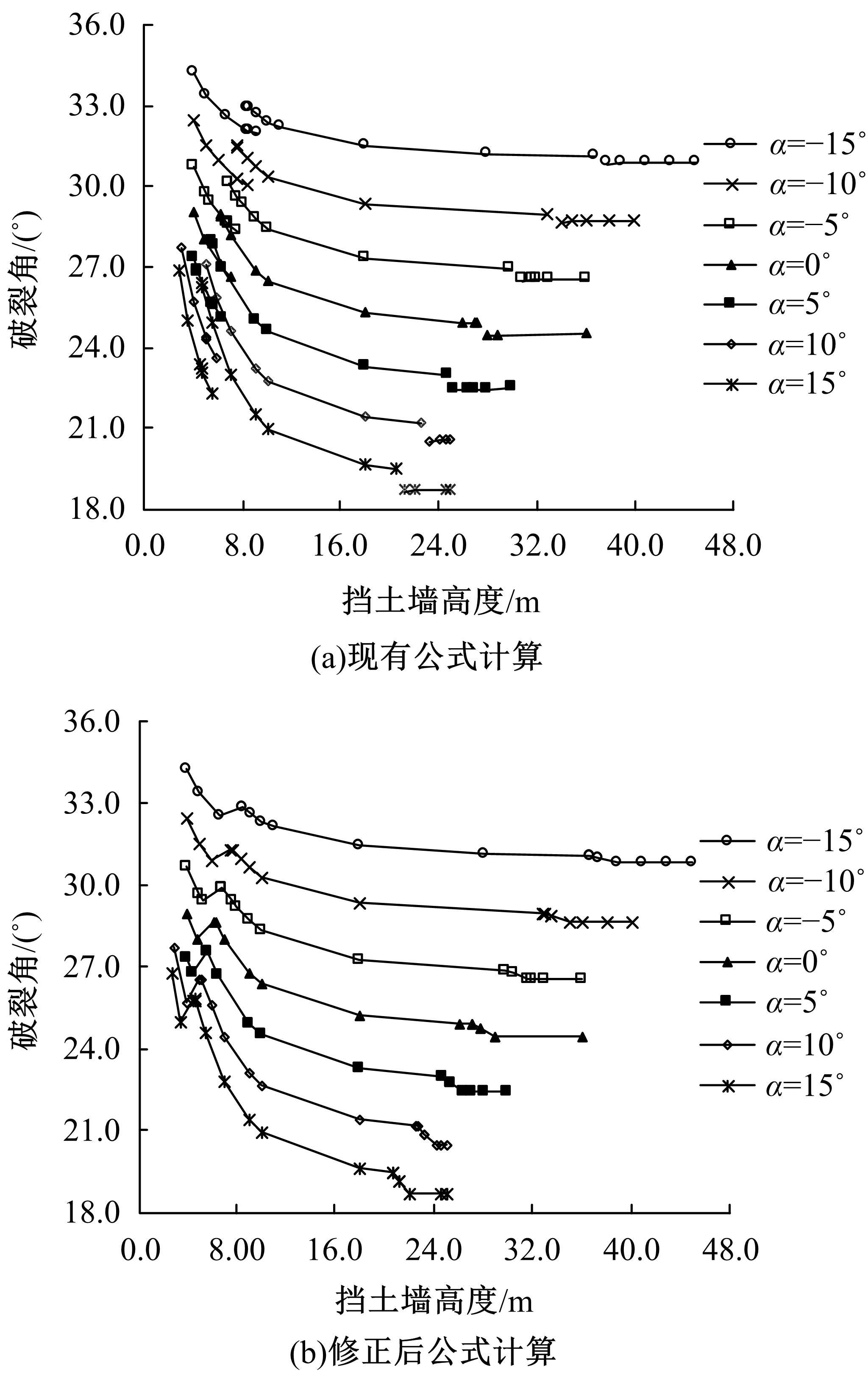
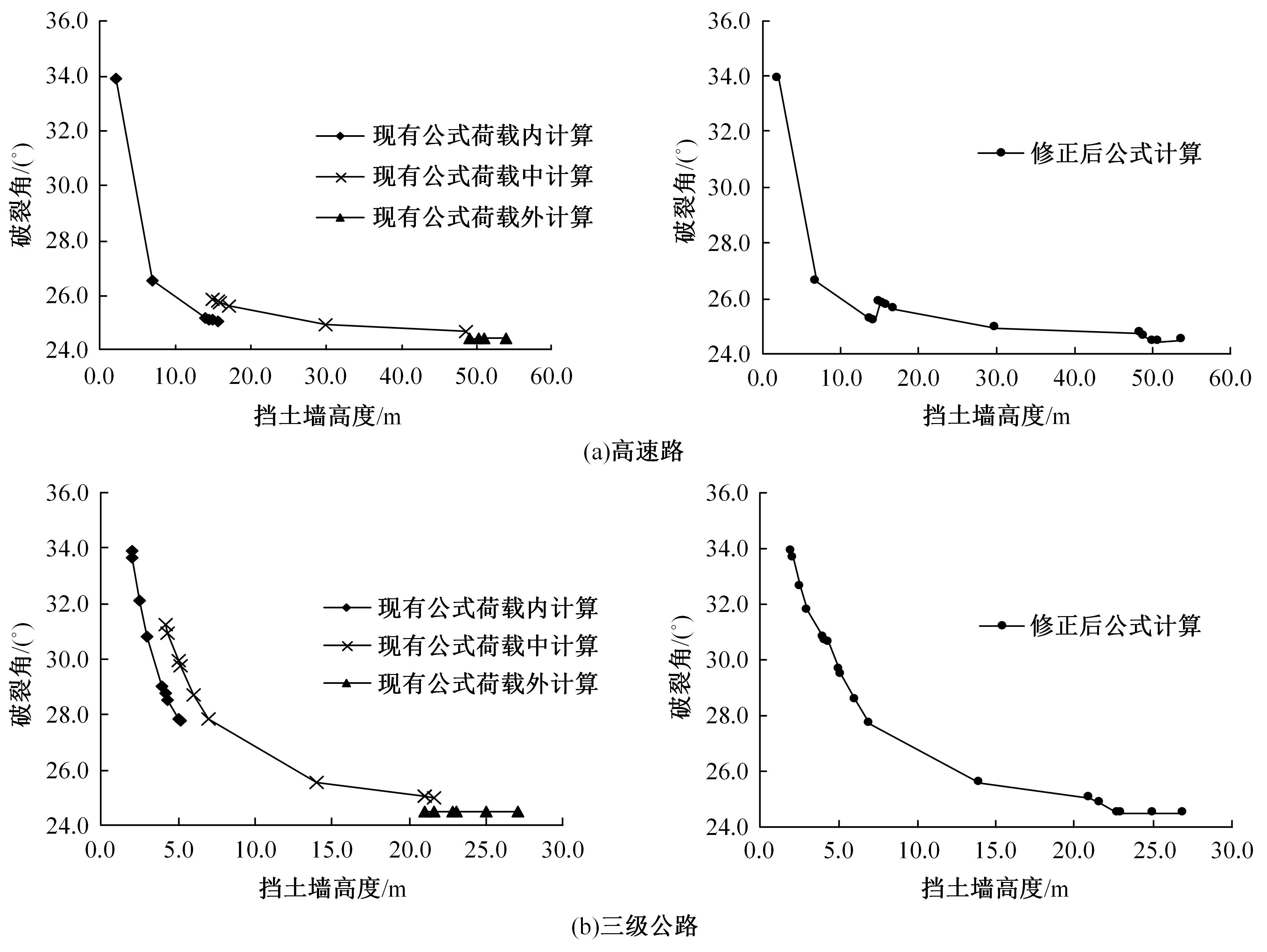
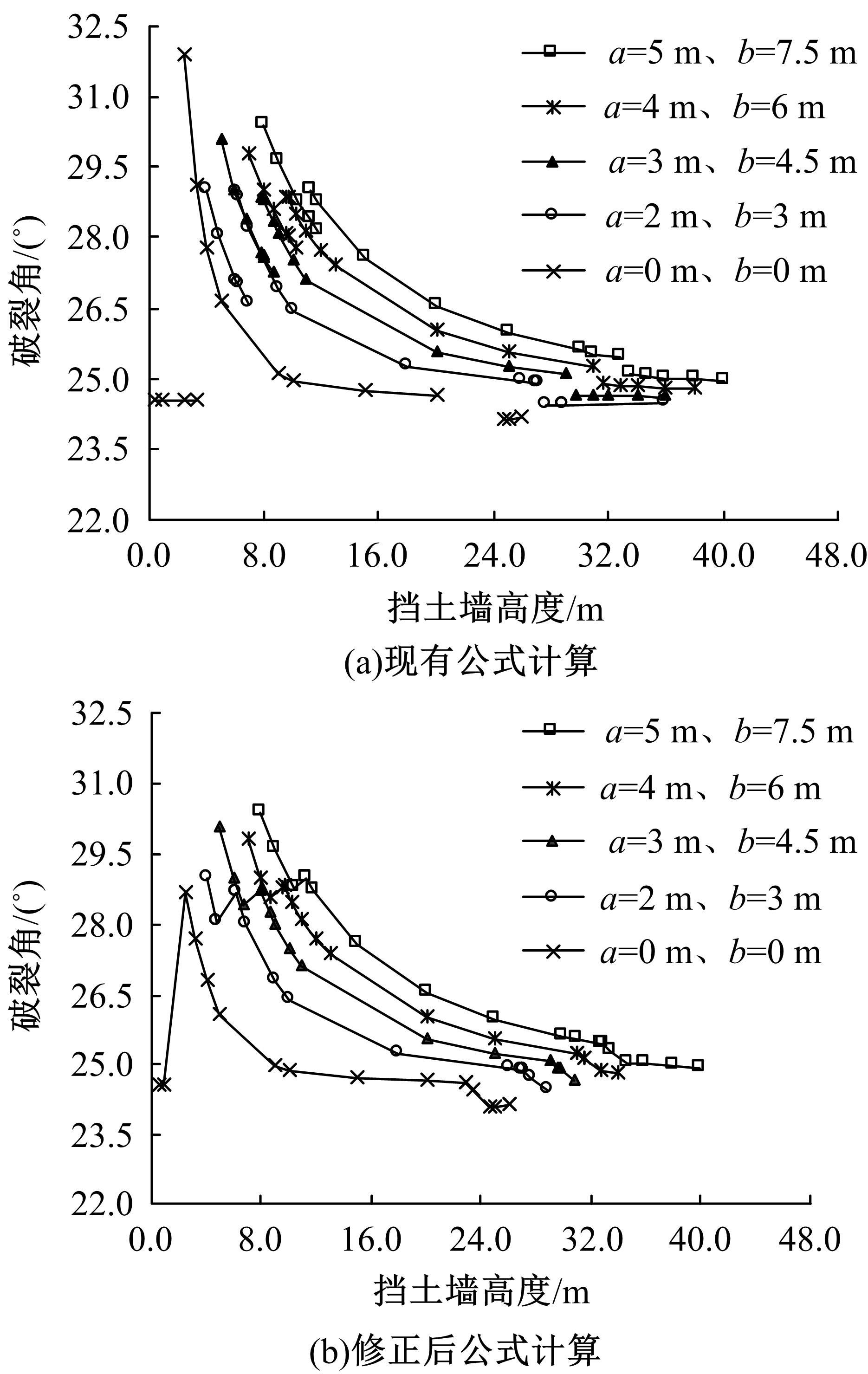
路堤挡土墙主动土压力计算方法修正
- 1.吉林建筑大学 交通科学与工程学院,长春 130118
2.吉林大学 交通学院,长春 130022
3.吉林省公路管理局,长春 130021
Modification of calculation method for active earth pressure on embankment retaining wall
Cheng-lin SHI1( ),Yong WANG1,Chun-li WU2(
),Yong WANG1,Chun-li WU2( ),Wen-zhu SONG3
),Wen-zhu SONG3
- 1.College of Transportation Science and Engineering,Jilin Jianzhu University,Changchun 130118,China
2.College of Transportation,Jilin University,Changchun 130022,China
3.Jilin Provincial Highway Administration Bureau,Changchun 130021,China
摘要:
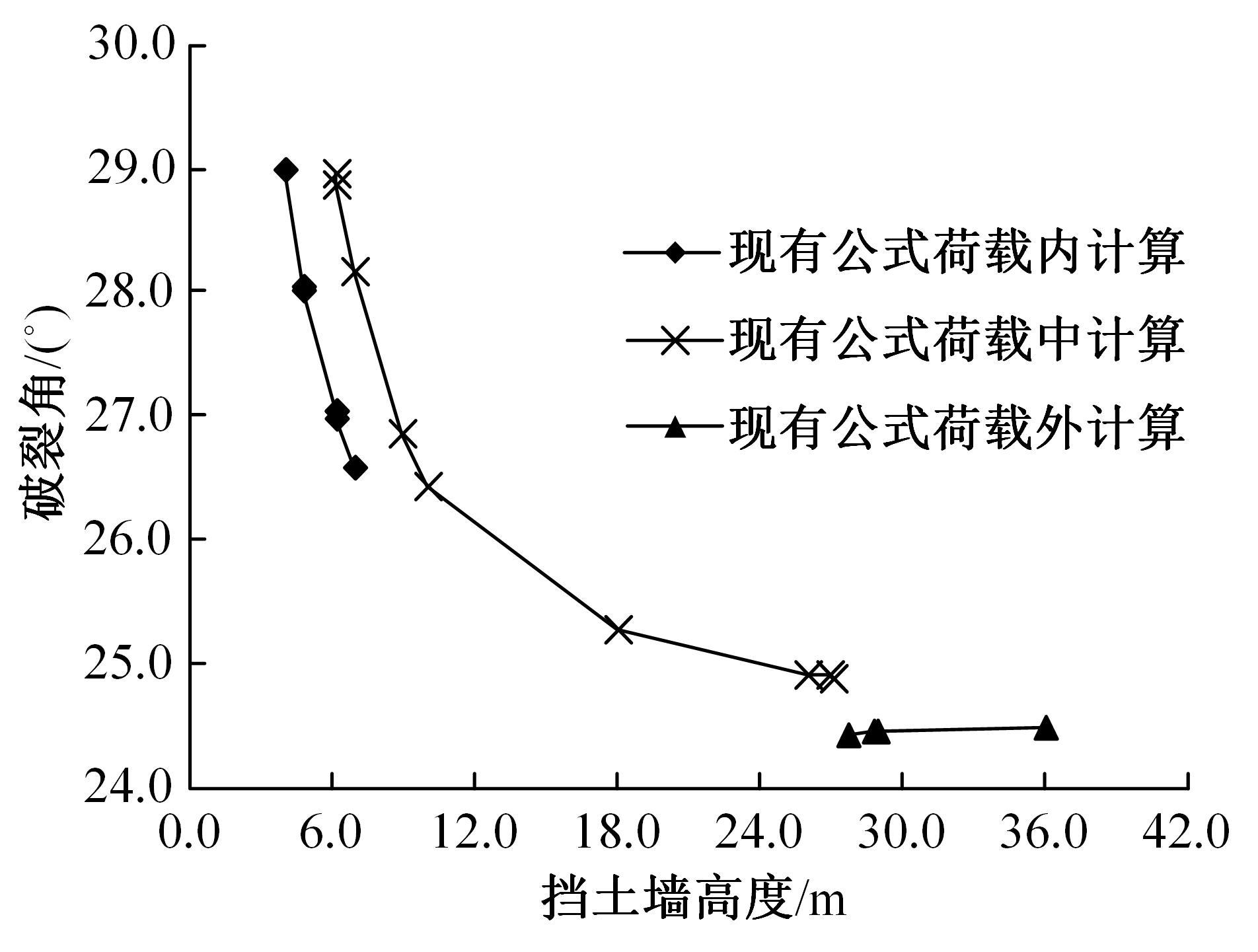
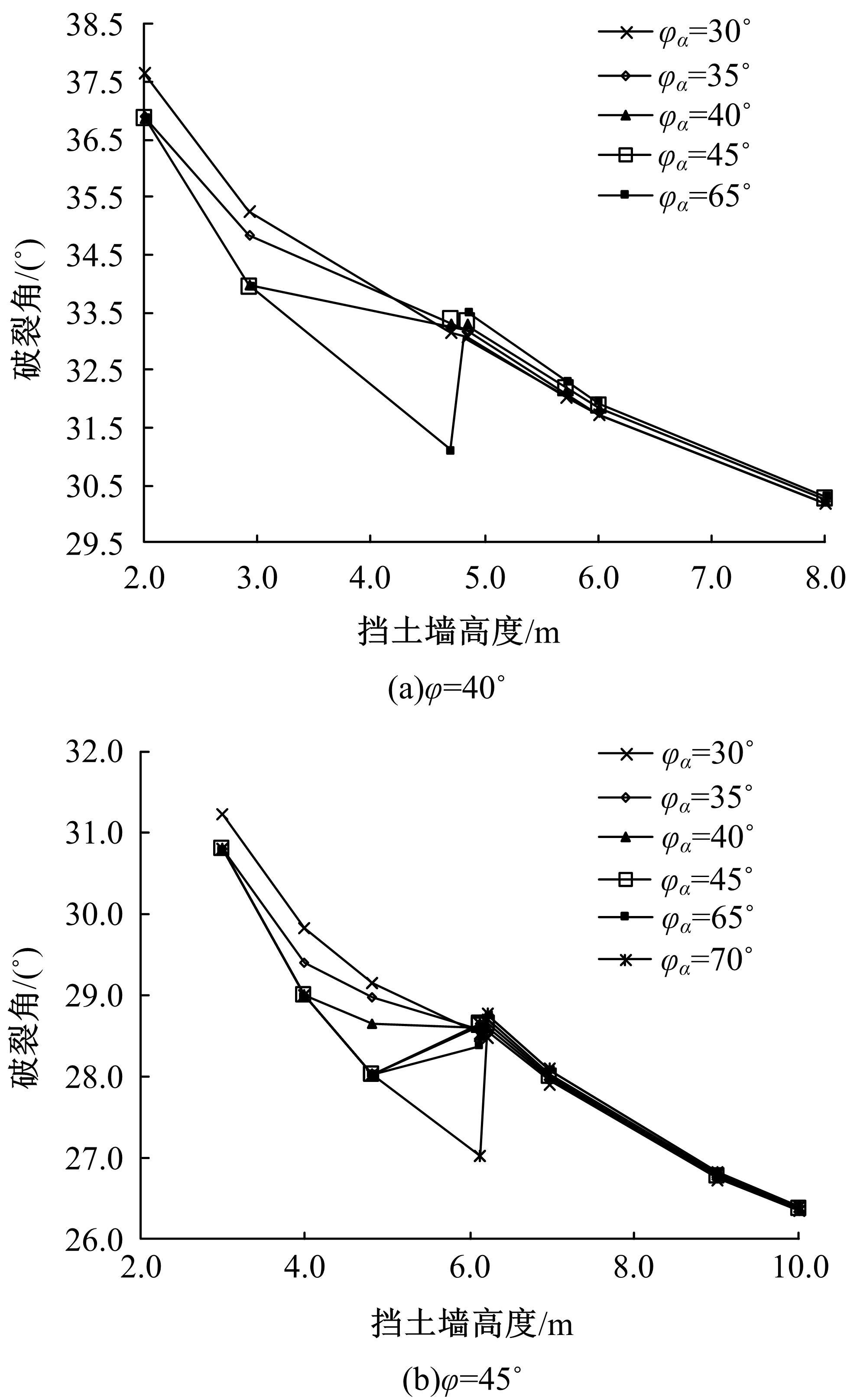
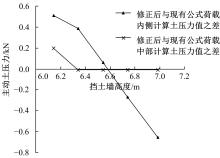
现有路堤挡土墙稳定性计算方法,均先假定墙后土体破裂面的位置,按照对应的公式计算出破裂角θ,再与假定的破裂角对比以确定计算结果。当挡土墙高度
中图分类号:
- U416
| 1 | 薛殿基,冯仲林. 挡土墙设计实用手册[M]. 北京: 中国建筑工业出版社,2008. |
| 2 | 彭明祥. 挡土墙主动土压力的库仑统一解[J]. 岩土力学, 2009, 30(2): 379-386. |
| Peng Ming-xiang. Coulumb's unified solution of active earth pressure on retaining wall[J]. Rock and Soil Mechanics, 2009, 30(2): 379-386. | |
| 3 | 顾慰慈. 挡土墙土压力计算手册[M]. 北京: 中国建材工业出版社, 2005. |
| 4 | 田恒银. 挡土墙主动土压力计算的研究[D]. 重庆:重庆大学土木工程学院, 2016. |
| Tian Heng-yin. Study on calculation of active earth pressure on retaining wall[D]. Chongqing: College of Civil Engineering, Chongqing University, 2016. | |
| 5 | Fathipour H, Siahmazgi A S, Payan M, et al. Limit analysis of modified pseudodynamic lateral earth pressure in anisotropic frictional medium using finite-element and second-order cone programming[J/OL]. [2021-01-05]. |
| 6 | Rao P P, Chen Q S, Zhou Y T, et al. Determination of active earth pressure on rigid retaining wall considering arching effect in cohesive backfill soil[J]. International Journal of Geomechanics, 2016, 16(3): 1-9. |
| 7 | 刘洋, 于鹏强. 刚性挡土墙平移模式的土拱形状与主动土压力分析[J].岩土力学, 2019, 40(2): 506-516, 528. |
| Liu Yang, Yu Peng-qiang. Analysis of soil arch shape and active earth pressure in translation mode of rigid retaining wall[J]. Rock and Soil Mechanics, 2019, 40(2): 506-516, 528. | |
| 8 | 谢明星, 郑俊杰, 曹文昭, 等.有限填土路堤挡土墙主动土压力研究[J].华中科技大学学报:自然科学版, 2019, 47(2): 1-6. |
| Xie Ming-xing, Zheng Jun-jie, Cao Wen-zhao, et al. Research on active earth pressure of retaining wall of limited fill embankment[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2019, 47(2): 1-6. | |
| 9 | 谢清泉, 刘昌清, 王卉, 等. 悬臂式挡土墙土压力计算方法对比研究[J]. 路基工程, 2020(5): 110-114, 125. |
| Xie Qing-quan, Liu Chang-qing, Wang Hui, et al. Comparative study on earth pressure calculation methods of cantilever retaining wall[J]. Subgrade Engineering, 2020(5):110-114, 125. | |
| 10 | 王闫超, 晏鄂川, 陆文博, 等. 无黏性有限土体主动土压力解析解[J]. 岩土力学, 2016, 37(9): 2513-2520. |
| Wang Yan-chao, Yan E-chuan, Lu Wen-bo, et al. Analytical solution for active earth pressure of non-cohesive finite soil[J]. Rock and Soil Mechanics, 2016, 37(9): 2513-2520. | |
| 11 | 顾嵋杰. 基于不同破裂面类型的挡土墙土压力的分析计算[J]. 西北水电, 2020(4):52-56. |
| Gu Mei-jie. Analysis and calculation of earth pressure on retaining wall based on different fracture surface types[J]. Northwest Hydropower, 2020(4):52-56. | |
| 12 | 竺明星, 姜开渝, 龚维明, 等. 考虑c-φ回填土坡面倾角影响的挡土墙非线性主动土压力研究[J]. 天津大学学报, 2019, 52(): 70-75. |
| Zhu Ming-xing, Jiang Kai-yu, Gong Wei-ming, et al. Study on nonlinear active earth pressure of retaining wall considering the influence of slope angle of c-φ backfill [J]. Journal of Tianjin University, 2019, 52(Sup.1): 70-75. | |
| 13 | 黄旺, 杨建军, 黄娟. 几种挡土墙主动土压力理论对比及墙体应力分析[J]. 长沙理工大学学报: 自然科学版, 2017, 14(3): 29-34. |
| Huang Wang, Yang Jian-jun, Huang Juan. Theoretical comparison and wall stress analysis of several retaining walls[J]. Journal of Changsha University of science and Technology(Natural Science Edition), 2017, 14(3): 29-34. | |
| 14 | 张东卿, 薛元, 罗强, 等. 中欧(法)挡土墙设计规范对比研究[J]. 铁道工程学报, 2020, 37(2): 30-34, 39. |
| Zhang Dong-qing, Xue Yuan, Luo Qiang, et al. Comparative study of China-Europe (French) retaining wall design code[J]. Journal of Railway Engineering Society, 2020, 37(2): 30-34, 39. | |
| 15 | 柯才桐, 陈奕柏, 朱嘉. 挡土墙土压力线性分布解[J]. 岩石力学与工程学, 2014, 33():3312-3317. |
| Ke Cai-tong, Chen Yi-bo, Zhu Jia. Linear distribution solution of earth pressure on retaining wall[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(Sup.1):3312-3317. | |
| 16 | 党发宁, 张乐, 王旭, 等. 基于弹性理论的有限位移条件下挡土墙上土压力解析[J]. 岩石力学与工程学报, 2020, 39(10): 2094-2103. |
| Dang Fa-ning, Zhang Le, Wang Xu, et al. Analysis of earth pressure on retaining wall under limited displacement conditions based on elastic theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(10): 2094-2103. | |
| 17 | 吴艾祺. 车辆动荷载作用下公路挡土墙的力学响应研究[D]. 西安:长安大学地质工程与测绘学院, 2019. |
| Wu Ai-qi. Research on the mechanical response of highway retaining walls under dynamic vehicle load[D]. Xi'an: College of Geological Engineering and Geomatics, Chang'an University, 2019. | |
| 18 | 刘宁, 刘杰. 国内外标准中砂性土内摩擦角确定方法对比[J]. 水运工程, 2021, 45(1): 42-47. |
| Liu Ning, Liu Jie. Comparison of methods for determining the internal friction angle of sandy soil in domestic and foreign standards[J]. Water Transport Engineering, 2021, 45(1): 42-47. | |
| 19 | 刘寒冰, 张互助, 王静. 失水干燥对路基压实黏质土抗剪强度特性的影响[J]. 吉林大学学报: 工学版, 2017, 47(2): 446-451. |
| Liu Han-bing, Zhang Hu-zhu, Wang Jing. Effect of dehydration and drying on shear strength characteristics of subgrade compacted clayey soil[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(2): 446-451. |
| [1] | 郭庆林,刘强,吴春利,李黎丽,李懿明,刘富春. 导电沥青及混合料裂缝局部温度场及愈合效果[J]. 吉林大学学报(工学版), 2022, 52(6): 1386-1393. |
| [2] | 姚玉权,仰建岗,高杰,宋亮. 基于性能-费用模型的厂拌再生沥青混合料优化设计[J]. 吉林大学学报(工学版), 2022, 52(3): 585-595. |
| [3] | 夏全平,高江平,罗浩原,张其功,李志杰,杨飞. 用于高模量沥青砼的复合改性硬质沥青低温性能[J]. 吉林大学学报(工学版), 2022, 52(3): 541-549. |
| [4] | 冉武平,陈慧敏,李玲,冯立群. 干湿循环下粗粒土回弹模量演变规律及模型预估和修正[J]. 吉林大学学报(工学版), 2021, 51(6): 2079-2086. |
| [5] | 董伟智,张爽,朱福. 基于可拓层次分析法的沥青混合料路用性能评价[J]. 吉林大学学报(工学版), 2021, 51(6): 2137-2143. |
| [6] | 许哲谱,杨群. 基于实时路况地图的短期养护作业开始时间优化[J]. 吉林大学学报(工学版), 2021, 51(5): 1763-1774. |
| [7] | 文畅平,任睆遐. 基于Lade模型的生物酶改良膨胀土双屈服面本构关系[J]. 吉林大学学报(工学版), 2021, 51(5): 1716-1723. |
| [8] | 王元元,孙璐,刘卫东,薛金顺. 测量路面三维纹理双目重构算法的约束改进[J]. 吉林大学学报(工学版), 2021, 51(4): 1342-1348. |
| [9] | 彭勇,杨汉铎,陆学元,李彦伟. 基于离散元法的空隙特征对沥青混合料虚拟剪切疲劳寿命的影响[J]. 吉林大学学报(工学版), 2021, 51(3): 956-964. |
| [10] | 朱伟刚,朱超,张亚球,魏海斌. 基于卷积格网曲面拟合滤波算法的数字高程模型构建及质量评价[J]. 吉林大学学报(工学版), 2021, 51(3): 1073-1080. |
| [11] | 程永春,李赫,李立顶,王海涛,白云硕,柴潮. 基于灰色关联度的矿料对沥青混合料力学性能的影响分析[J]. 吉林大学学报(工学版), 2021, 51(3): 925-935. |
| [12] | 宫亚峰,逄蕴泽,王博,谭国金,毕海鹏. 基于吉林省路况的新型预制装配式箱涵结构的力学性能[J]. 吉林大学学报(工学版), 2021, 51(3): 917-924. |
| [13] | 阳恩慧,徐加秋,唐由之,李奥,邱延峻. 温拌剂对沥青断裂和老化性能的影响[J]. 吉林大学学报(工学版), 2021, 51(2): 604-610. |
| [14] | 戴文亭,司泽华,王振,王琦. 剑麻纤维水泥加固土的路用性能试验[J]. 吉林大学学报(工学版), 2020, 50(2): 589-593. |
| [15] | 方宇,孙立军. 基于生存分析的城市桥梁使用性能衰变模型[J]. 吉林大学学报(工学版), 2020, 50(2): 557-564. |
|
||