基于响应面与遗传算法的主轴系统动力学建模及参数修正

doi:10.13229/j.cnki.jdxbgxb20210311

摘要/Abstract

摘要：

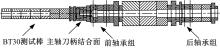
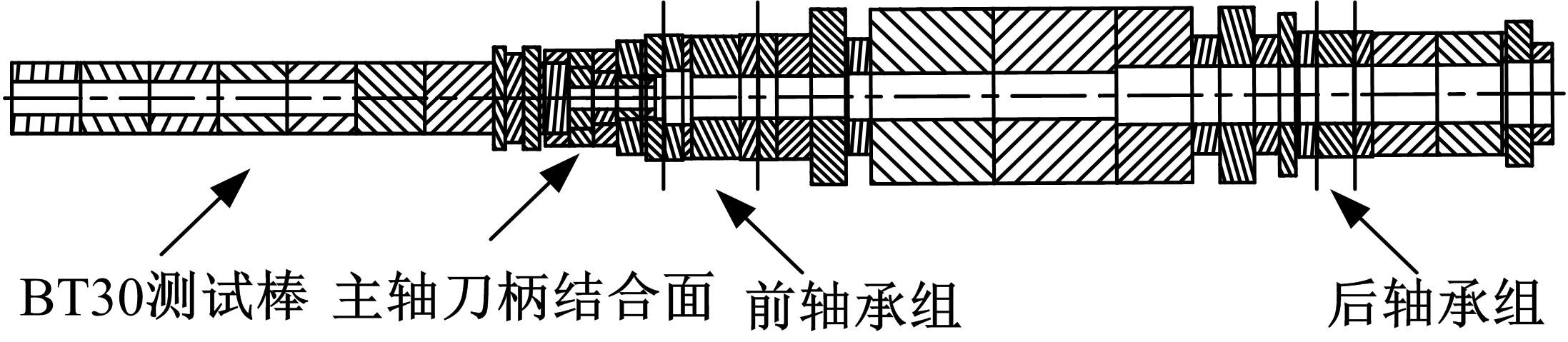
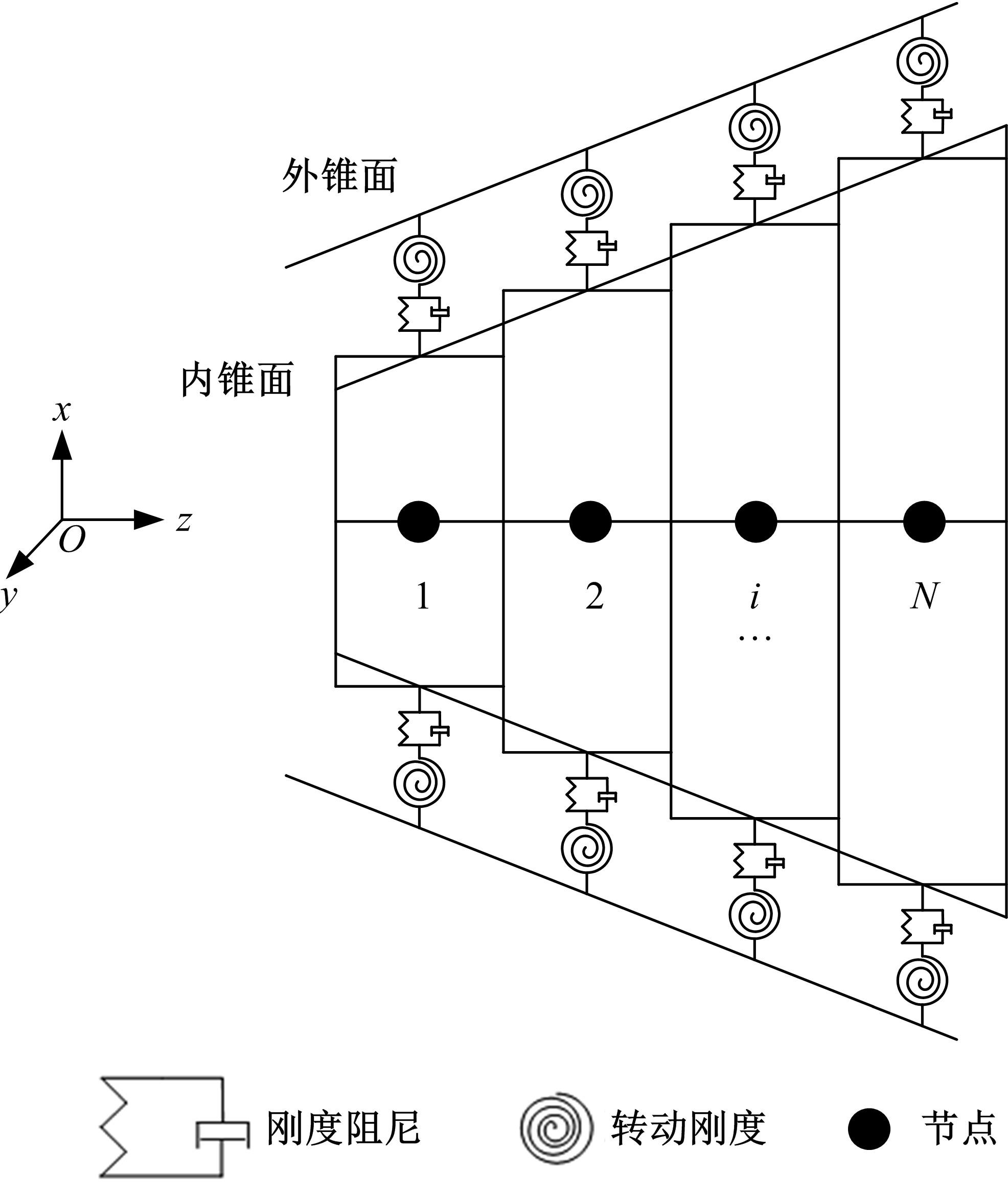
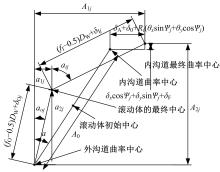
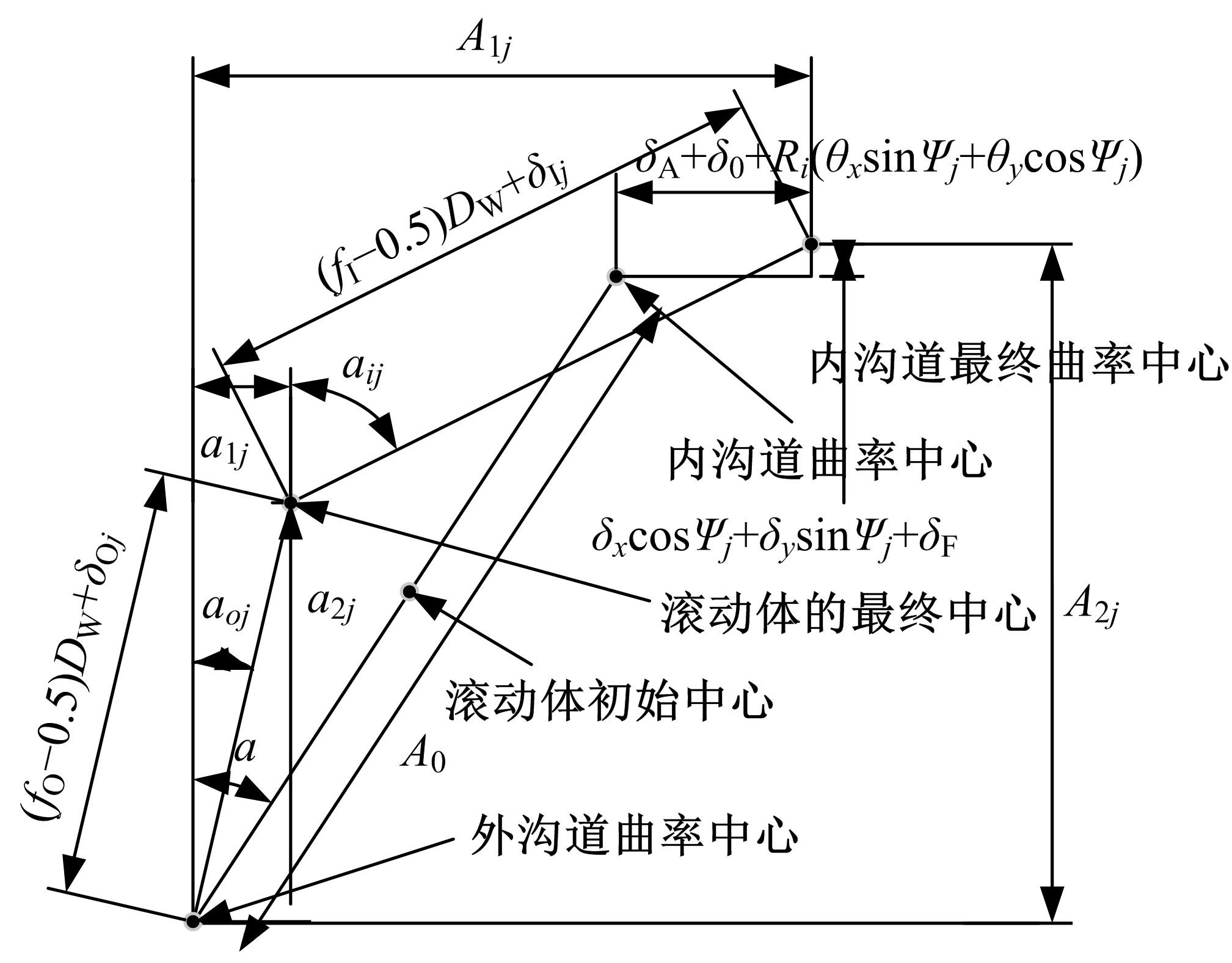
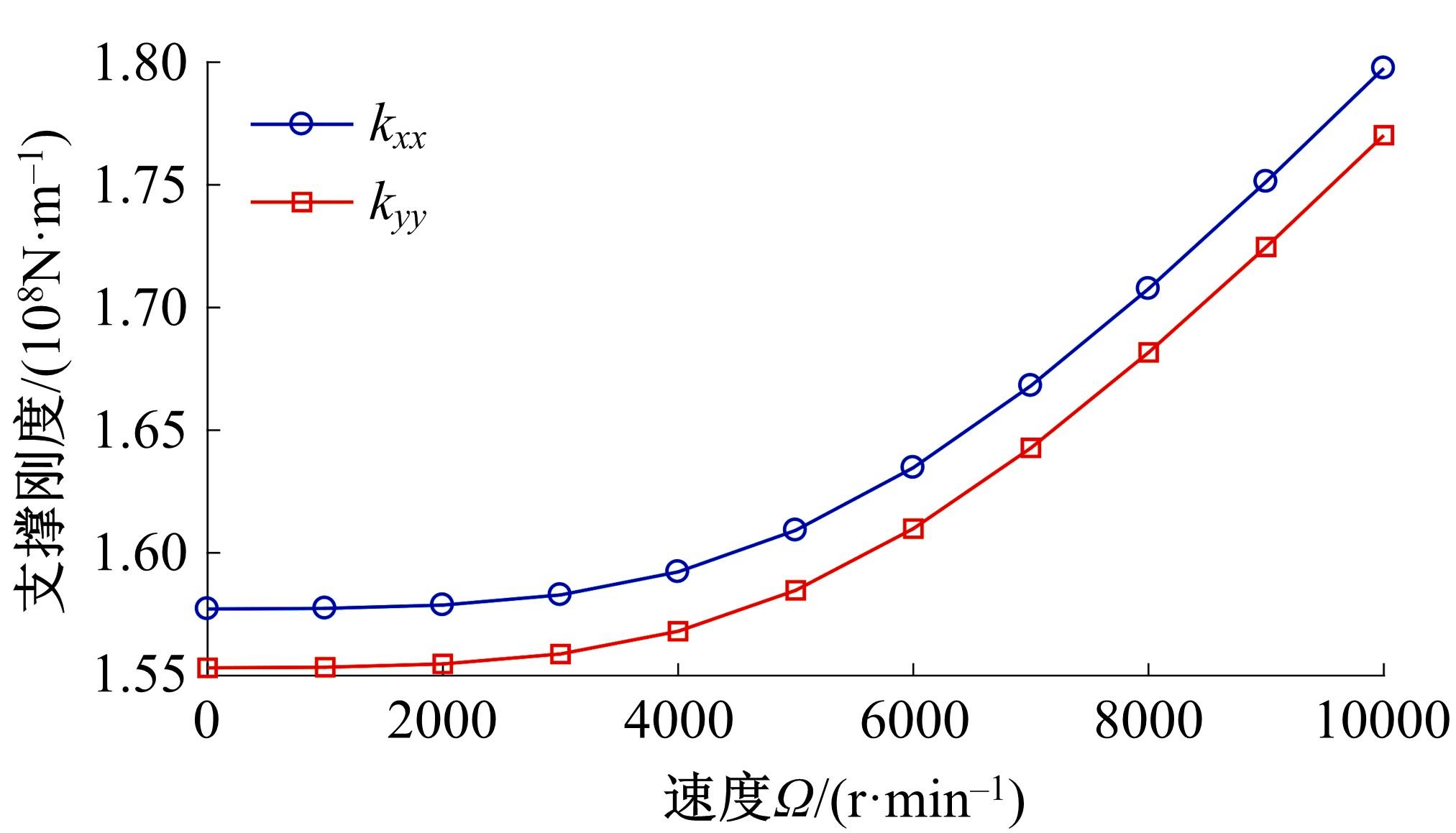
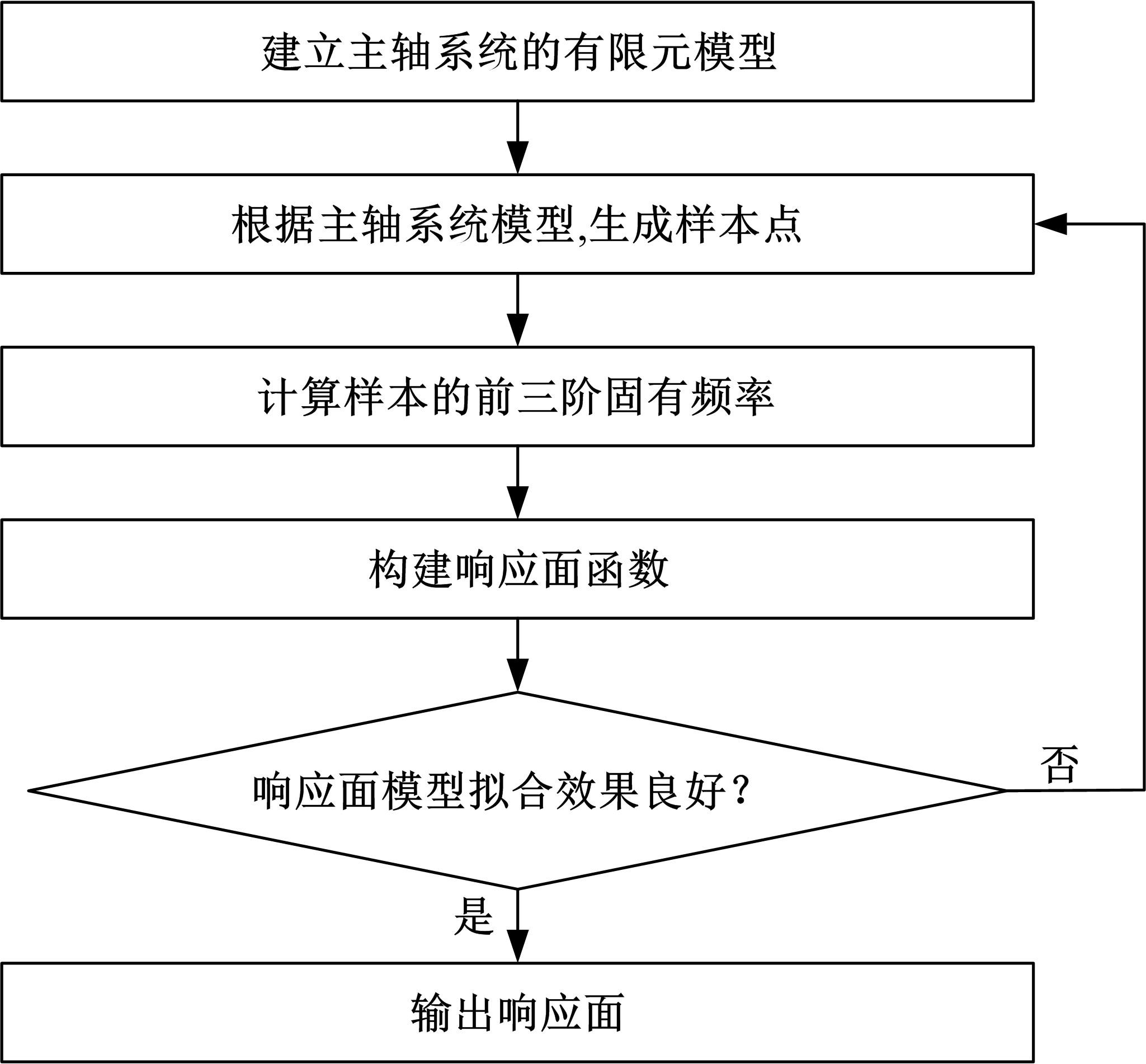
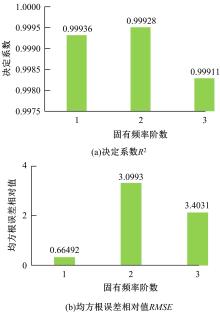
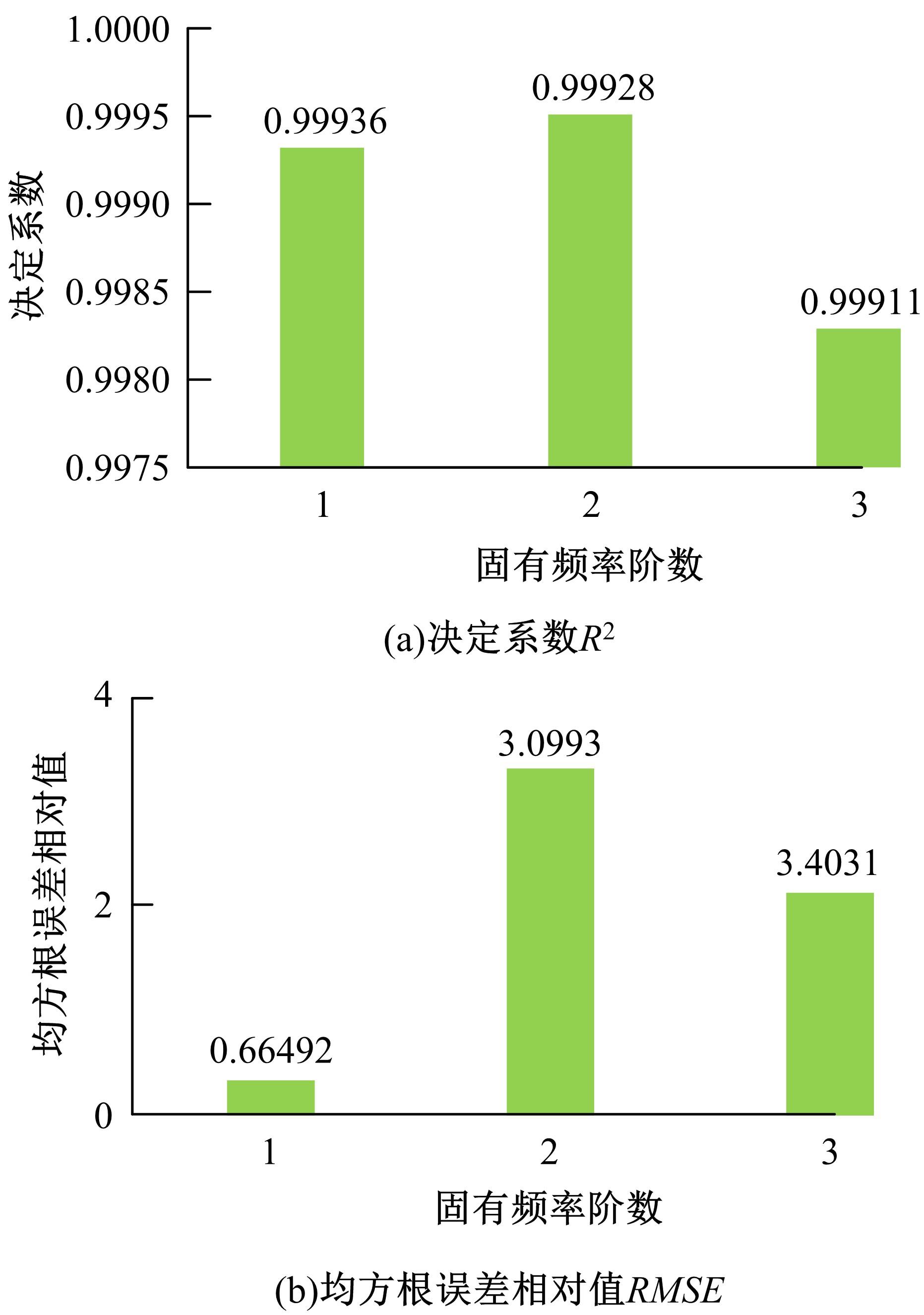
针对在建立主轴系统的动力学模型时采用简化处理带来较大的误差问题，提出了一种融合响应面与遗传算法的主轴系统动力学建模方法。首先，考虑切削过程中主轴与刀柄之间的结合面刚度以及主轴轴承的支撑刚度，建立主轴系统的动力学模型；其次，通过对比刚性连接和柔性连接时主轴系统的前三阶固有频率，分析影响主轴系统动力学特性的主要因素；然后，基于主轴系统的动力学模型构造接触刚度的样本点，以样本点中的主轴与刀柄的结合面刚度作为输入参数，主轴系统的一阶、二阶和三阶固有频率作为输出参数，采用非参数回归方法构造响应面模型，利用决定系数和均方根误差的相对值检验响应面的精度；最后，通过多目标遗传算法修正主轴-刀柄结合面的刚度，以此为基础修正主轴系统的动力学模型，从而提高主轴系统动力学模型的精度。以某主轴系统为例，通过对比修正前后的分析精度，验证基于响应面和遗传算法的主轴动力学分析的准确性。

关键词: 主轴系统, 动力学分析, 响应面, 多目标遗传算法

Abstract:

Considering that the simplified processing in the process of establishing the dynamic model of the spindle system will lead to a large error， a dynamic modeling method based on response surface and genetic algorithm is proposed. Firstly， the dynamic model of the spindle system is established by considering the stiffness of the spindle-holder joint surface and the bearing support stiffness. Secondly， the main factors that affect the accuracy of dynamics analysis are developed by comparing the first three natural frequencies of the spindle system model with rigid and flexible connections. Then， sample points of contact stiffness are constructed based on the dynamics model of the spindle system， and the stiffness of the spindle-holder joint in the sample point is used as the input parameter， then the first， second， and third order natural frequency are used as the output parameters， and the non-parametric regression method is used to fit the response surface. The relative value of the determination coefficient and the root mean square error is used to test the accuracy of the response surface. The multi-objective genetic algorithm is used to update the stiffness of spindle-holder joint， which is used to update the dynamic model of the spindle system. Finally， a case study shows that the proposed method based on the fusion response surface methodology and optimization algorithm has higher analysis accuracy.

Key words: spindle system, dynamics analysis, response surface, multi-objective genetic algorithm

中图分类号:

TG659

陈传海,姚国祥,金桐彤,申桂香,于立娟,田海龙. 基于响应面与遗传算法的主轴系统动力学建模及参数修正[J]. 吉林大学学报(工学版), 2022, 52(10): 2278-2286.

Chuan-hai CHEN,Guo-xiang YAO,Tong-tong JIN,Gui-xiang SHEN,Li-juan YU,Hai-long TIAN. Dynamic modeling and parameter updating of machine tool spindle system based on response surface methodology and genetic algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2022, 52(10): 2278-2286.

图/表 18

图1

图2

图3

图4

图5

表1

主轴-刀柄结合面的刚度"

参数	接触刚度/（N·m^-1）	参数	转动刚度/（N·m^-1）
k₁_xk₁_y	1.5×10⁷	$k 1 ψ k 1 θ$	1.66×10⁴
k₂_xk₂_y	1.22×10⁷	$k 2 ψ k 2 θ$	1.38×10⁴
k₃_xk₃_y	9.95×10⁷	$k 3 ψ k 3 θ$	1.15×10⁴
k₄_xk₄_y	8.07×10⁷	$k 4 ψ k 4 θ$	9.62×10³

表1

图6

图7

图8

图9

图10

表2

表3

图11

图12

表4

修正后的主轴-刀柄结合面刚度"

参数	接触刚度/（N·m^-1）	参数	转动刚度/（N·m^-1）
k₁_xk₁_y	9.28×10⁶	$k 1 ψ k 1 θ$	3.5×10⁴
k₂_xk₂_y	5.77×10⁶	$k 2 ψ k 2 θ$	3.04×10⁴
k₃_xk₃_y	2.917×10⁶	$k 3 ψ k 3 θ$	2.3×10⁴
k₄_xk₄_y	5.212×10⁶	$k 4 ψ k 4 θ$	2.21×10⁴

表4

表5

图13

参考文献 22

1	杨兆军,陈传海,陈菲,等. 数控机床可靠性技术的研究进展[J]. 机械工程学报,2013,49(20):130-139.
	Yang Zhao-jun, Chen Chuan-hai, Chen Fei,et al. Progress in the research of reliability technology of machine tools[J]. Journal of Mechanical Engineering,2013,49(20):130-139.
2	Altintas Y. Manufacturing Automation: Metal Cutting Mechanics, Machine Tool Vibrations,and CNC Design[M]. Cambridge:Cambridge University Press, 2000.
3	Altintas Y, Cao Yu-zhong. A general method for the modeling of spindle-bearing systems[J]. Journal of Mechanical Design,2004,126(6):1089-1104.
4	Magara Traore M,裴永臣,谭庆昌. 高速微小孔钻头动态应力特性[J]. 吉林大学学报: 工学版, 2005, 35(6):606-612.
	Magara Traore M, Pei Yong-chen, Tan Qing-chang. Dynamic stress characteristic of high-speed micro-holedrill[J]. Journal of Jilin University(Engineering and Technology Edition), 2005,35(6):606-612.
5	Jiang Shu-yun, Mao He-bing. Investigation of variable optimum preload for a machine tool spindle[J]. International Journal of Machine Tools & Manufacture, 2010, 50(1): 19-28.
6	蔡力钢,马仕明,赵永胜,等. 多约束状态下重载机械式主轴有限元建模及模态分析[J]. 机械工程学报,2012,48(3):165-173.
	Cai Li-gang, Ma Shi-ming, Zhao Yong-sheng,et al. Finite element modeling and modal analysis of heavy-duty mechanical spindle under multiple constraints[J]. Journal of Mechanical Engineering, 2012, 48(3):165-173.
7	姜彦翠,刘献礼,吴石,等. 考虑结合面和轴向力的主轴系统动力学特性[J]. 机械工程学报,2015,51(19):66-74.
	Jiang Yan-cui, Liu Xian-li, Wu Shi,et al. Dynamics characteristics of the spindle system with the interface and axial milling force[J]. Journal of Mechanical Engineering,2015, 51(19): 66-74.
8	Kim T R, Wu S M, Eman K F. Identification of joint parameters for a taper joint[J]. Journal of Engineering for Industry,1989,111(3): 282-287.
9	孙伟,汪博,闻邦椿. 高速主轴系统静止及运转状态下动力学特性对比分析[J]. 机械工程学报,2012,48(11):146-152.
	Sun Wei, Wang Bo, Wen Bang-chun. Comparative analysis of dynamics characteristics for static and operation state of high-speed spindle system[J]. Journal of Mechanical Engineering,2012,48(11): 146-152.
10	Hanna I M, Agapiou J S, Stephenson D A. Modeling the HSK toolholder-spindle interface[J]. Journal of Manufacturing Science & Engineering,2002,124(3):734-744.
11	赵万华,杜超,张俊,等. 主轴转子系统动力学解析建模方法[J]. 机械工程学报,2013,49(6):44-51.
	Zhao Wan-hua, Du Chao, Zhang Jun, et al. Analytical modeling method of dynamics for the spindle rotor system[J]. Journal of Mechanical Engineering,2013,49(6):44-51.
12	曹宏瑞,何正嘉. 机床-主轴耦合系统动力学建模与模型修正[J]. 机械工程学报,2012,48(3):88-94.
	Cao Hong-rui, He Zheng-jia. Dynamic modeling and model updating of coupled systems between machine tool and its spindle[J]. Journal of Mechanical Engineering,2012,48(3):88-94.
13	Inman D J. Engineering Vibration[M]. New York:McGraw-Hill, 1994.
14	张学良. 机械结合面动态特性及应用[M]. 北京:中国科学技术出版社,2002.
15	Jones A B. A general theory for elastically constrained ball and radial roller bearings under arbitrary load and speed conditions[J]. ASME J Basic Engineering, 1960, 82(2):309-320.
16	Harris T A, Kotzalas M N. Rolling Bearing Analysis[M]. 5th ed. NewYork, USA:Taylor & Francis,2007.
17	蒋兴奇. 主轴轴承热特性及对速度和动力学性能影响的研究[D]. 杭州:浙江大学机械学院,2001.
	Jiang Xing-qi. Study on heat characteristics of spindle bearings and influences on speed and dynamics[D]. Hangzhou: College of Mechanical Engineering,Zhejiang University,2001.
18	赵春江,崔国华,王国强,等. 基于接触角变量传递分析方法的角接触球轴承动态特性求解[J]. 吉林大学学报:工学版,2009,39(2):368-371.
	Zhao Chun-jiang, Cui Guo-hua, Wang Guo-qiang,et al. Solution of the dynamic characteristic of angular-contact ball bearing based on analysis of contact angle variable deliver[J]. Journal of Jilin University (Engineering and Technology Edition),2009,39(2):368-371.
19	Yang Yang, Cao Long-chao, Wang Chao-chao,et al.Multi-objective process parameters optimization of hot-wire laser welding using ensemble of metamodels and NSGA-II[J]. Robotics and Computer-Integrated Manufacturing,2018,53:141-152.
20	Montgomery, Douglas C, Montgomery D C. Design and Analysis of Experiments[M]. London:Wiley,1976.
21	Fonseca Carlos M, Fleming Peter J. Non-Linear system identification with multi objective genetic algorithms[C]∥Proceedings of the 13th World Congress of the International Federation of Automatic Control,San Francisco, USA, 1996,214-219.
22	Deb K, Jain H,et al. An evolutionary many-objective optimization a lgorithm using reference-point based non-dominated sorting approach,part ii: handling constraints and extending to an adaptive approach[J]. IEEE Transactions on Evolutionary Computation,2014,18(4):602-622.

相关文章 15

[1]	程亚兵,陈璐翔,葛平玉,杨泽宇,曹鹏宇. 双相正时套筒链的动力学仿真分析及磨损失效[J]. 吉林大学学报(工学版), 2022, 52(4): 781-788.
[2]	姚玉权,仰建岗,高杰,宋亮. 基于性能-费用模型的厂拌再生沥青混合料优化设计[J]. 吉林大学学报(工学版), 2022, 52(3): 585-595.
[3]	章子玲,胡雄,亓寅,王微,陶志强,刘志峰. 基于向量投影响应面的数控机床几何误差分配方法[J]. 吉林大学学报(工学版), 2022, 52(2): 384-391.
[4]	耿端阳,牟孝栋,张国栋,王宗源,朱俊科,徐海刚. 小麦联合收获机清选机理分析与优化试验[J]. 吉林大学学报(工学版), 2022, 52(1): 219-230.
[5]	杨开宇,刘伟,王天皓,于显利,高印寒,马喜来. 一种多导体传输线串扰不确定性问题的计算方法[J]. 吉林大学学报(工学版), 2021, 51(2): 747-753.
[6]	蔡中义,孟凡响,陈庆敏,赵轩. 复杂钩舌锻件近净成形的预锻形状优化设计[J]. 吉林大学学报(工学版), 2020, 50(1): 84-90.
[7]	马芳武,韩露,周阳,王世英,蒲永锋. 采用聚乳酸复合材料的汽车零件多材料优化设计[J]. 吉林大学学报(工学版), 2019, 49(5): 1385-1391.
[8]	那景新, 浦磊鑫, 范以撒, 沈传亮. 湿热环境对Sikaflex-265铝合金粘接接头失效强度的影响[J]. 吉林大学学报(工学版), 2018, 48(5): 1331-1338.
[9]	宫亚峰, 申杨凡, 谭国金, 韩春鹏, 何钰龙. 不同孔隙率下纤维土无侧限抗压强度[J]. 吉林大学学报(工学版), 2018, 48(3): 712-719.
[10]	周放, 宋传学, 梁天唯, 肖峰. 采用NSGA-II算法的车载复合电源参数匹配[J]. 吉林大学学报(工学版), 2017, 47(5): 1336-1343.
[11]	周杰, 罗艳, 王珣, 王辉, 李洋, 陶亚平. 基于响应面的封头冲压成形工艺多目标优化[J]. 吉林大学学报(工学版), 2016, 46(1): 205-212.
[12]	刘坤, 赵建琛, 曹恩国, 韩宣. 基于下肢动力学检测分析的站起康复训练机器人控制[J]. 吉林大学学报(工学版), 2015, 45(3): 837-843.
[13]	程亚兵，王洋，李磊，安立持，殷帅兵. 汽车V型发动机用正时链传动系统的设计[J]. 吉林大学学报(工学版), 2015, 45(1): 139-144.
[14]	那景新, 高剑峰. 基于局部搜索和整体优化的客车杆件截面参数正向设计[J]. 吉林大学学报(工学版), 2014, 44(6): 1564-1570.
[15]	王利民, 肖志刚, 刘宇欣, 李杰, 孙旭, 申勋业, 李佳栋. 响应面法优化板栗基营养米挤压加工参数[J]. 吉林大学学报(工学版), 2013, 43(02): 550-556.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

验证条件	一阶频率	二阶频率	三阶频率
相对误差/%	30.3	15.5	35.4
仿真值/Hz	395	1157	1414
试验值/Hz	303	1002	1044

验证条件	一阶频率	二阶频率	三阶频率
相对误差/%	23.7	16.1	28.4
仿真值/Hz	231	1163	1341
试验值/Hz	303	1002	1044

验证条件	一阶频率	二阶频率	三阶频率
相对误差/%	4.6	5.59	3.2
优化后的仿真值/Hz	289	1058	1077
实验值/Hz	303	1002	1044