基于弹性波传播和谱单元法的桁架结构损伤检测

doi:10.13229/j.cnki.jdxbgxb20210471

摘要/Abstract

摘要：

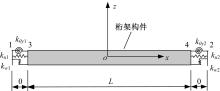
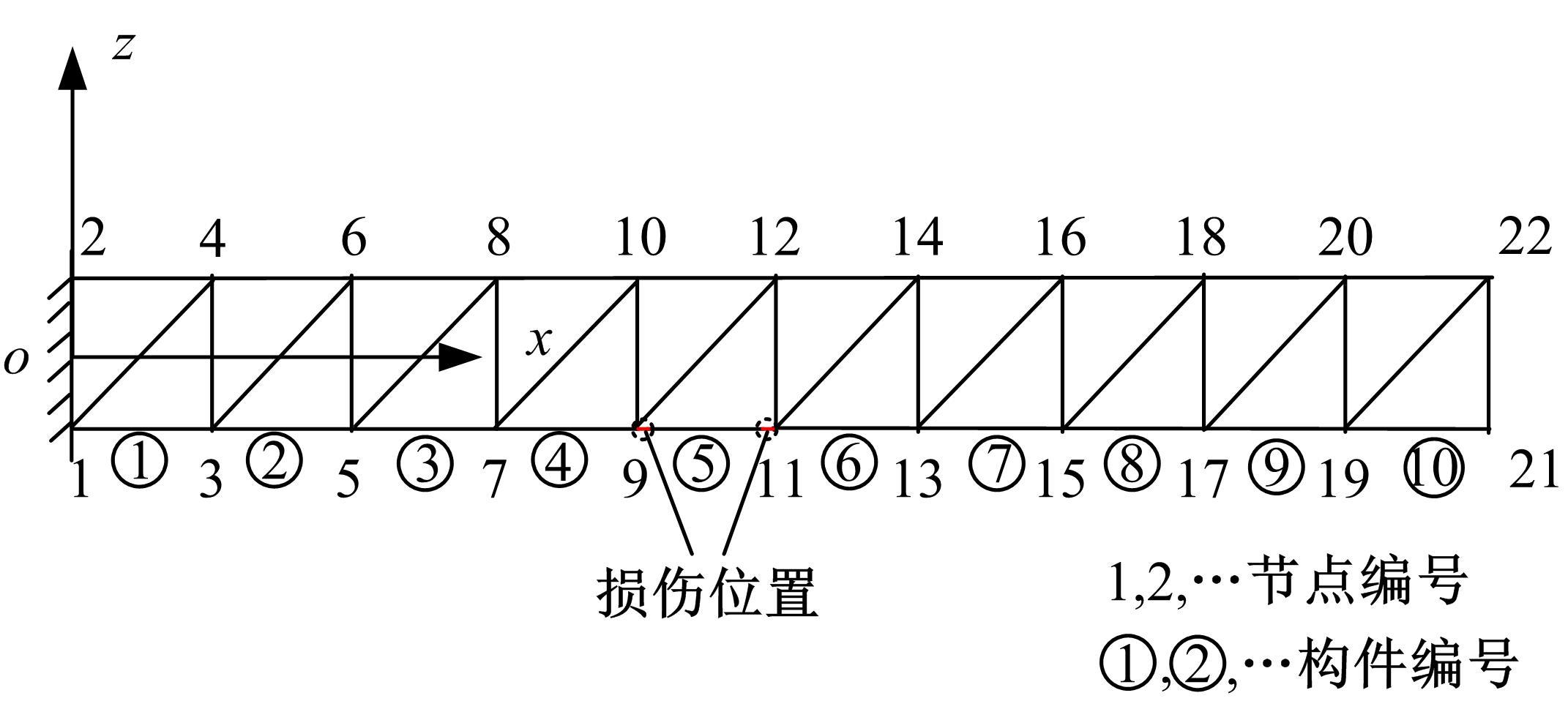
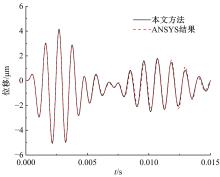
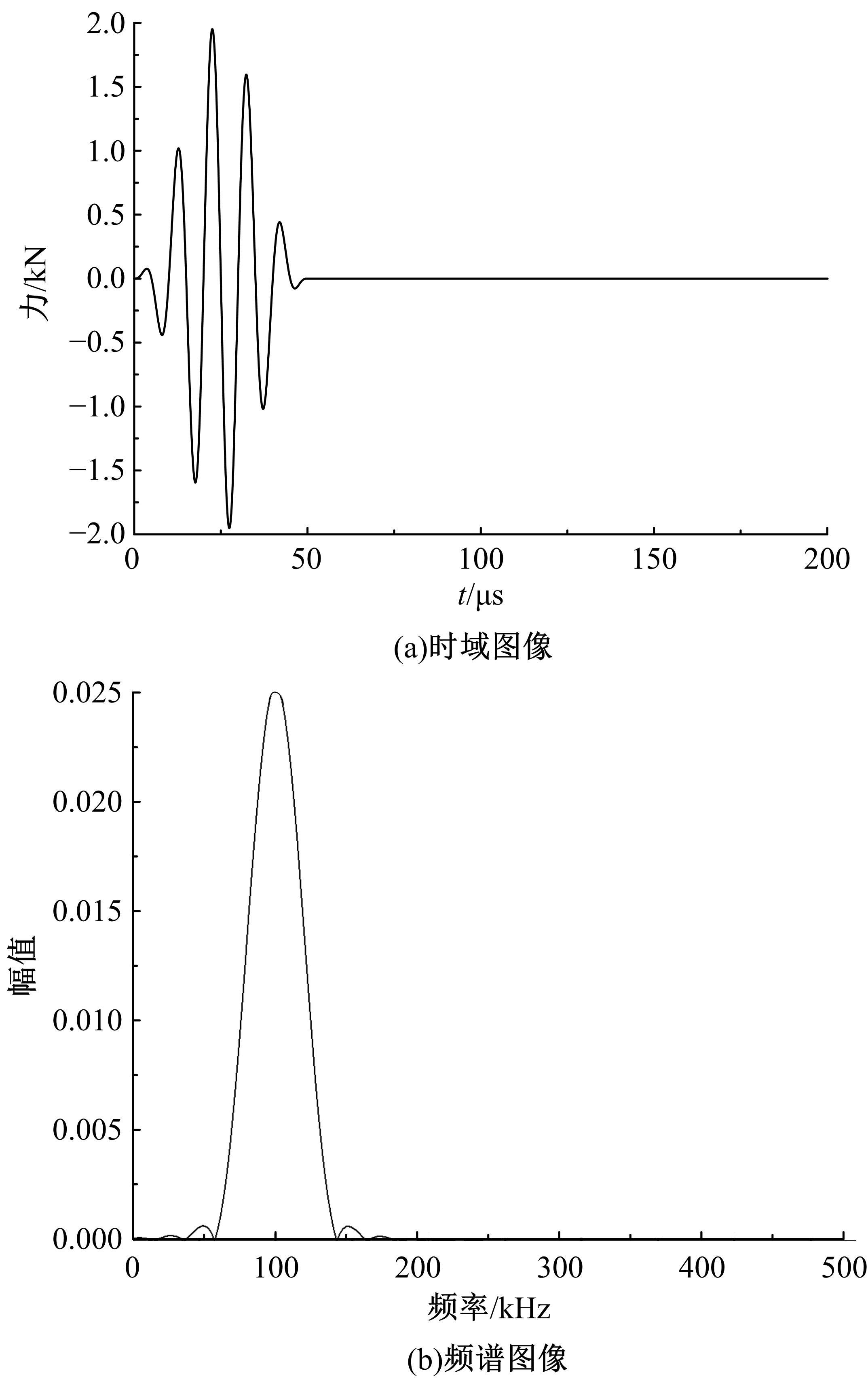
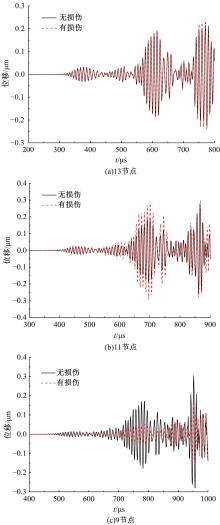
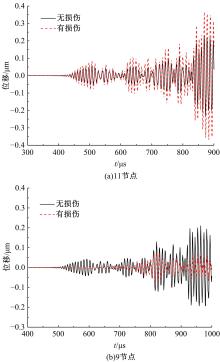
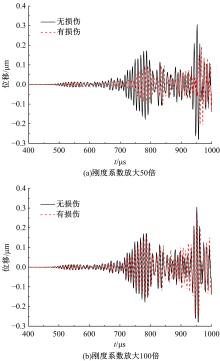
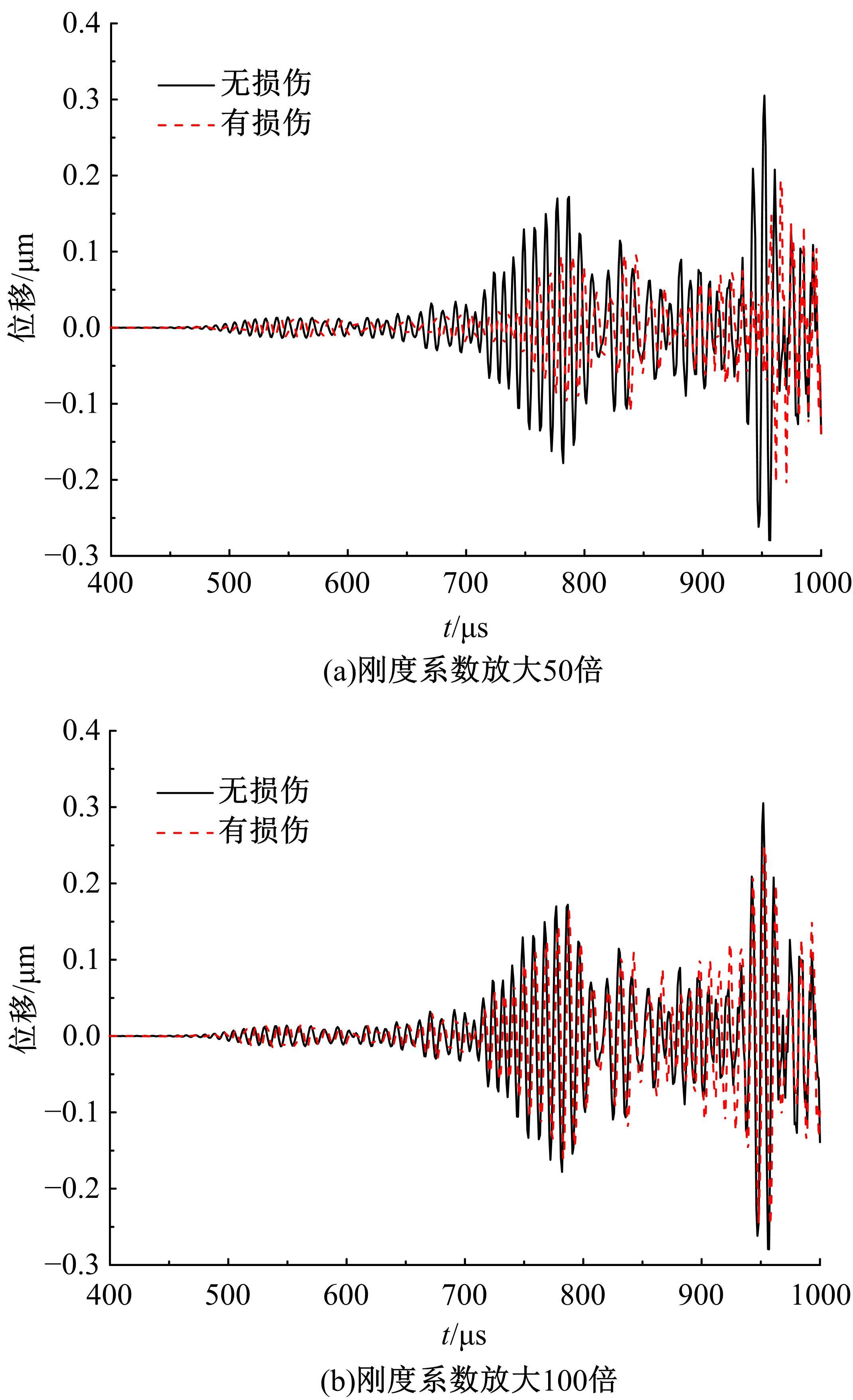
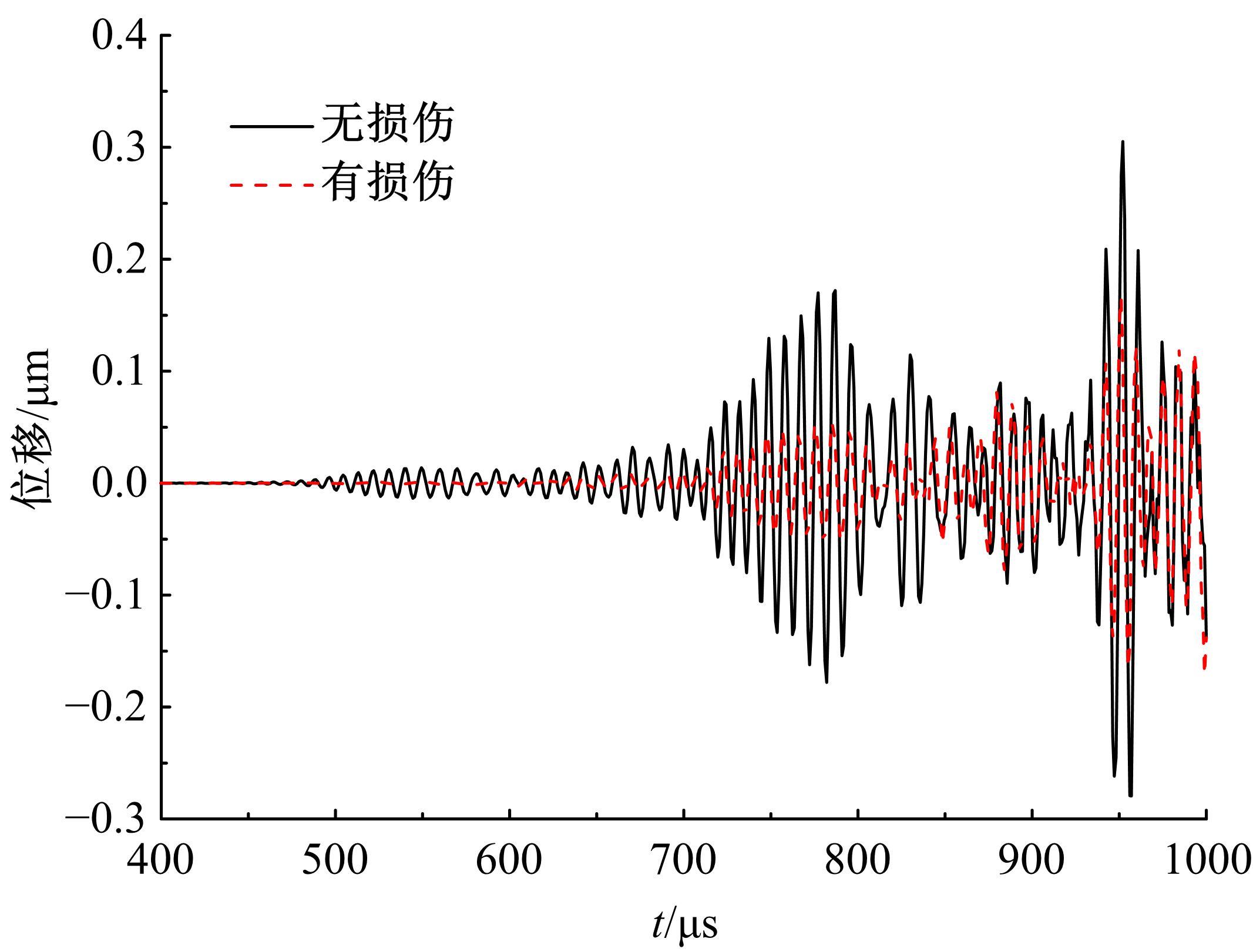
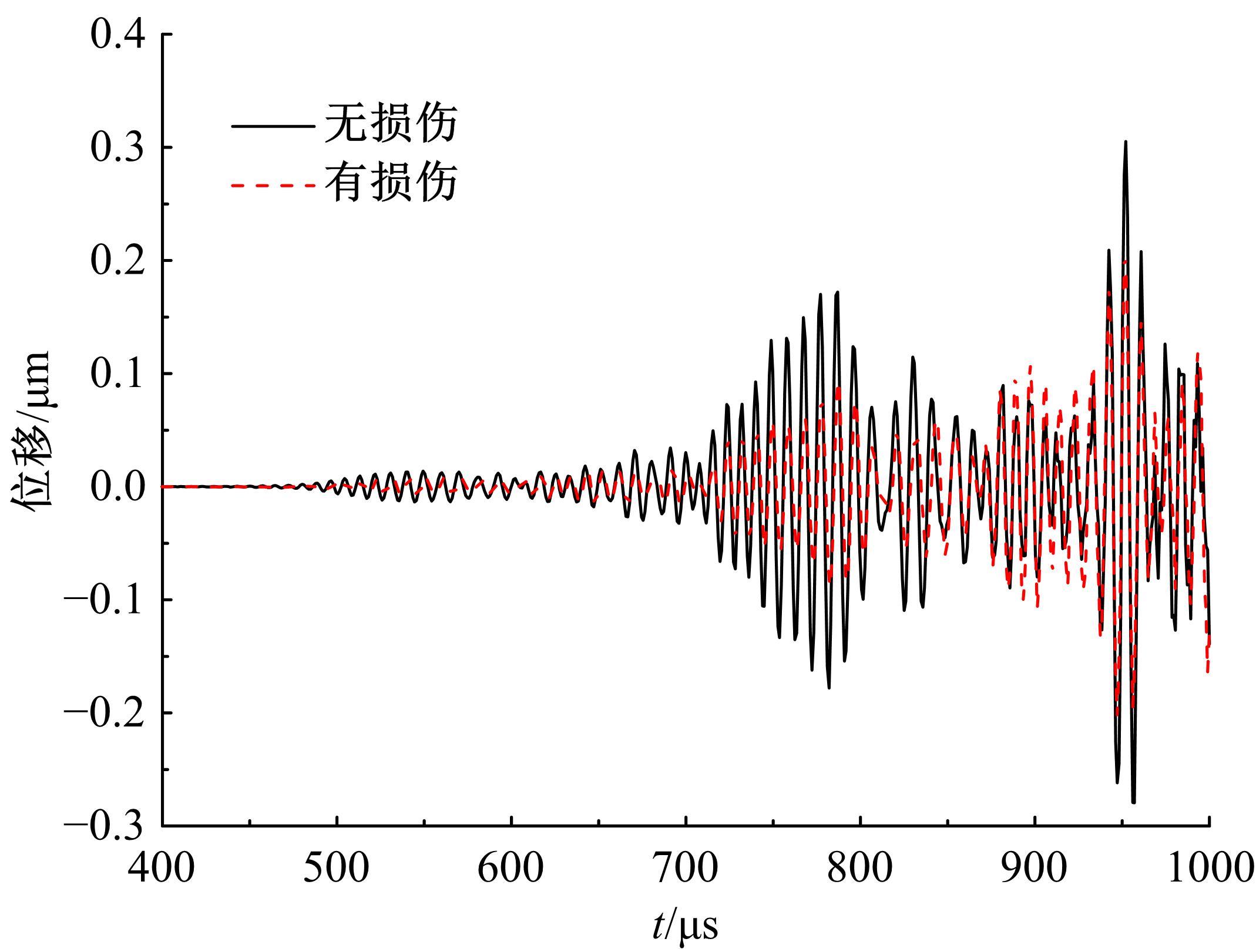
为了准确、及时地对桁架结构在长期服役后出现的构件和节点损伤进行检测，本文考虑了损伤引起的节点刚度下降，采用六自由度方向的线性弹簧模拟损伤后的节点，基于谱单元法建立了带有节点损伤的桁架结构动力学模型。对桁架结构施加窄带脉冲激励以激发结构内高频弹性波的传播，采用数值Laplace逆变换方法获取结构的时域响应。结果表明，弹性波在通过两端含有受损节点的构件时，其传播会受到一定的阻碍，导致桁架节点位移幅值的改变和首波到达节点时间的延迟，通过分析节点损伤引起的弹性波在桁架中传播的变化情况，可以实现桁架结构的损伤检测。

关键词: 结构工程, 桁架结构, 弹性波传播, 谱单元法, 损伤检测

Abstract:

Truss structures are prone to damages of components and joints after long-term service, so it is necessary to detect the damages of the structure accurately and timely. Considering the stiffness reduction of joints caused by damage, linear springs in six-axis directions are used to simulate the damaged joints, and the spectral element method based on Laplace transform is used to establish the dynamic model of truss structure with damaged joints. A narrow-band pulse excitation is applied to the truss structure to excite the propagation of high-frequency elastic wave in the structure. The time-domain response of the structure is obtained by using the numerical inverse Laplace transform method. The results show that, when the elastic wave passes through the component with damaged joints at both ends, the propagation will be hindered to a certain extent, resulting in the change of displacement amplitude of truss nodes and the delay of the arrival time of the first wave. By analyzing the change of elastic wave propagation in truss caused by joint damage, the damage detection of truss structure can be realized.

Key words: structural engineering, truss structure, elastic wave propagation, spectral element method, damage detection

中图分类号:

O327

刘福寿,魏琦,徐文婷,谭国金. 基于弹性波传播和谱单元法的桁架结构损伤检测[J]. 吉林大学学报(工学版), 2021, 51(6): 2087-2095.

Fu-shou LIU,Qi WEI,Wen-ting XU,Guo-jin TAN. Damage detection of truss structures based on elastic wave propagation and spectral element method[J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(6): 2087-2095.

图/表 11

图1

图2

表1

图3

图4

图5

图6

图7

图8

图9

图10

参考文献 26

1	Liu F S, Wang L B, Jin D P, et al. Equivalent micropolar beam model for spatial vibration analysis of planar repetitive truss structure with flexible joints[J]. International Journal of Mechanical Sciences, 2019, 165:No.105202.
2	金栋平, 刘福寿, 文浩, 等. 空间结构动力学等效建模与控制[M]. 北京: 科学出版社, 2021.
3	姜东,徐宇,王桂伦,等. 锁定状态下球铰连接桁架的刚度性能[J]. 东南大学学报: 自然科学版, 2019, 49 (5):820-825.
	Jiang Dong, Xu Yu, Wang Gui-lun, et al. Stiffness performance of ball hinged joint trusses under locking condition[J]. Journal of Southeast University (Natural Science Edition), 2019, 49(5):820-825.
4	周剑萍, 王亮. 大跨度主-副桁架钢结构的地震反应探讨分析[J]. 地震工程学报, 2019, 41(3):626-630.
	Zhou Jian-ping, Wang Liang. Discussion and analysis of seismic response of large-span main and auxiliary steel-truss structures[J]. China Earthquake Engineering Journal, 2019, 41(3):626-630.
5	胡长远, 唐和生, 薛松涛,等. 桁架结构可靠性优化设计的微分演化算法[J]. 江苏大学学报:自然科学版, 2013,34(2): 234-238, 243.
	Hu Chang-yuan, Tang He-sheng, Xue Song-tao, et al. Differential evolution algorithm of reliability optimization for truss structure[J]. Journal of Jiangsu Univeristy(Natural Science Edition), 2013,34(2): 234-238, 243.
6	綦宝晖, 邬瑞锋, 蔡贤辉,等. 一种桁架结构损伤识别的柔度阵法[J]. 计算力学学报, 2001, 18(1): 42-47.
	Qi Bao-hui, Wu Rui-feng, Cai Xian-hui, et al. A flexible matrix method for damage identification of truss structures[J]. Chinese Journal of Computational Mechanics, 2001, 18(1): 42-47.
7	Nguyen K D, Chan T H T, Thambiratnam D P, et al. Damage identification in a complex truss structure using modal characteristics correlation method and sensitivity-weighted search space[J]. Structural Health Monitoring, 2019, 18(1):49-65.
8	谢甫哲, 周广杰, 顾斌,等. 钢框架连续倒塌分析中全焊接刚性节点的组件模型[J]. 江苏大学学报:自然科学版, 2020,41(4):466-472.
	Xie Fu-Zhe, Zhou Guang-jie, Gu Bin, et al. Component-based model of all-welded joint in progressive collapse analysis of steel frames[J]. Journal of Jiangsu Univeristy(Natural Science Edition),2020,41(4):466-472.
9	谭国金. 中小跨径梁式桥动力检测技术及损伤识别方法研究[D]. 长春:吉林大学交通学院, 2009.
	Tan Guo-jin. Dynamic detection technique and damage identification method for beam bridges with small and medium span[D]. Changchun: College of Transportation, Jilin University, 2009.
10	谭国金, 姜霖, 吴春利, 等. 移动车辆作用下带有裂缝的多片梁式桥动力响应分析[J]. 吉林大学学报:工学版,2020, 50(6):2147-2158.
	Tan Guo-jin, Jiang Lin, Wu Chun-li, et al. Dynamic response analysis of multiple beam bridge with cracks under moving vehicles[J]. Journal of Jilin University (Engineering and Technology Edition), 2020, 50(6):2147-2158.
11	申林, 李万恒, 赵尚传. 基于模态柔度参数的连续梁桥损伤识别方法[J]. 吉林大学学报:工学版, 2019, 49(1):66-72.
	Shen Lin, Li Wan-heng, Zhao Shang-chuan. Damage identification of continuous beam bridge based on modal flexibility recognition[J]. Journal of Jilin University (Engineering and Technology Edition), 2019, 49(1):66-72.
12	王术新, 姜哲. 裂缝梁固有频率分析[J]. 江苏大学学报:自然科学版, 2003,24(4):30-33.
	Wang Shu-xin, Jiang Zhe. Analysis on natural frequencies of cracked beams[J]. Journal of Jiangsu Univeristy(Natural Science Edition), 2003,24(4):30-33.
13	Ostachowicz W, Kudela P, Krawczuk M, et al. Guided Waves in Wtructures for SHM: the Time-domain Spectral Element Method[M]. Chichester: John Wiley & Sons Ltd, 2011.
14	Liu X L, Jiang Z W. Design of a PZT patch for measuring longitudinal mode impedance in the assessment of truss structure damage[J]. Smart Materials & Structures, 2009, 18(12):No.125017.
15	吴冠男, 裘群海, 王腾,等. 弹性波在螺栓搭接结构中传播行为的数值模拟[J]. 应用力学学报, 2018, 35(3):458-464, 682.
	Wu Guan-nan, Qiu Qun-hai, Wang Teng, et al. Numerical simulation of elastic wave propagation in bolted lapped structures[J]. Chinese Journal of Applied Mechanics, 2018, 35(3):458-464, 682.
16	Stawiarski A, Barski M, Pająk P. Fatigue crack detection and identification by the elastic wave propagation method[J]. Mechanical Systems & Signal Processing, 2017, 89:119-130.
17	王腾. 基于谱单元的弹性波传播分析及损伤检测研究[D]. 西安:西北工业大学材料学院, 2016.
	Wang Teng. Analysis of elastic wave propagation and damage detection based on spectral element[D]. Xi′an: Institute of Materials, Northwestern Polytechnical University, 2016.
18	Lee U. Spectral Element Method in Structural Dynamics[M]. Singapore: John Wiley & Sons (Asia), 2009.
19	Krawczuk M, Palacz M, Ostachowicz W. The dynamic analysis of a cracked Timoshenko beam by the spectral element method[J]. Journal of Sound & Vibration, 2003, 264(5): 1139-1153.
20	彭海阔, 孟光. 基于谱元法的梁结构中Lamb波传播特性研究[J]. 噪声与振动控制, 2009, 29(6):62-66.
	Peng Hai-kuo, Meng Guang. Study on Lamb wave propagation in beam structure based on spectral element method[J]. Noise and Vibration Control, 2009, 29(6):62-66.
21	Zhu X P, Rizzo P, Marzani A, et al. Ultrasonic guided waves for nondestructive evaluation/structural health monitoring of trusses[J]. Measurement Science & Technology, 2010, 21(4):No.045701.
22	Igawa H, Komatsu K, Yamaguchi I, et al. Wave propagation analysis of frame structures using the spectral element method[J]. Journal of Sound and Vibration, 2004, 277(4/5):1071-1081.
23	Yang Z B, Chen X F, Li X, et al. Wave motion analysis in arch structures via wavelet finite element method[J]. Journal of Sound & Vibration, 2014, 333(2):446-469.
24	Brancik L. Programs for fast numerical inversion of Laplace transforms in MATLAB language environment[C]∥Proceedings of the 7th Conference MATLAB'99, Czech Republic, Prague, 1999:27-39.
25	胡海岩. 结构阻尼模型及系统时域动响应[J]. 应用力学学报, 1993, 9(1): 34-43, 136.
	Hu Hai-yan. Structural damping model and system dynamic response in time domain[J]. Chinese Journal of Applied Mechanics, 1993, 9(1):34-43, 136.
26	Doyle J F. Wave Propagation in Structures Spectral Analysis Using Fast Discrete Fourier Transforms[M]. New York: Springer, 1997.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

刚度系数	数值
k_u₁、k_u₂/（10⁷ N·m^-1）	1
k_v₁、k_v₂/（10⁷ N·m^-1）	2
k_w₁、k_w₂/（10⁷ N·m^-1）	3
k_θx₁、k_θx₂/（10³ N·m·rad^-1）	1
k_θy₁、k_θy₂/（10³ N·m·rad^-1）	2
k_θz₁、k_θz₂/（10³ N·m·rad^-1）	3

[1]	樊学平,杨光红,肖青凯,刘月飞. 大跨桥梁主梁失效概率分析的最优R-Vine Copula[J]. 吉林大学学报(工学版), 2021, 51(4): 1296-1305.
[2]	于江,赵志浩,秦拥军. 基于声发射和分形的钢筋混凝土受剪梁损伤[J]. 吉林大学学报(工学版), 2021, 51(2): 620-630.
[3]	熊二刚,徐涵,谭赐,王婧,丁若愚. 基于弹塑性应力场理论的钢筋混凝土梁受剪承载力[J]. 吉林大学学报(工学版), 2021, 51(1): 259-267.
[4]	樊学平,屈广,刘月飞. 应用新数据同化算法的桥梁极值应力预测[J]. 吉林大学学报(工学版), 2020, 50(2): 572-580.
[5]	杨德磊,童乐为. 支管受轴向受拉工况下CHS-CFSHS T型节点应力集中系数计算公式[J]. 吉林大学学报(工学版), 2019, 49(6): 1891-1899.
[6]	戴岩, 聂少锋, 周天华. 带环梁的方钢管约束钢骨混凝土柱-钢梁节点滞回性能有限元分析[J]. 吉林大学学报(工学版), 2018, 48(5): 1426-1435.
[7]	杨昕卉, 薛伟, 郭楠. 钢板增强胶合木梁的抗弯性能[J]. 吉林大学学报(工学版), 2017, 47(2): 468-477.
[8]	王少杰, 徐赵东, 李舒, 王凯洋，Dyke Shirley J. 基于应变监测的连续梁支承差异沉降识别[J]. 吉林大学学报(工学版), 2016, 46(4): 1090-1096.
[9]	宿晓萍，王清. 复合盐浸-冻融-干湿多因素作用下的混凝土腐蚀破坏[J]. 吉林大学学报(工学版), 2015, 45(1): 112-120.
[10]	姜浩, 郭学东. 基于地震激励的混凝土桥梁模态参数识别[J]. 吉林大学学报(工学版), 2011, 41(增刊2): 185-188.