自锚式悬索桥的面内稳定性

doi:10.13229/j.cnki.jdxbgxb20180178

摘要/Abstract

摘要：

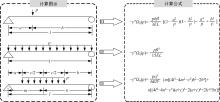
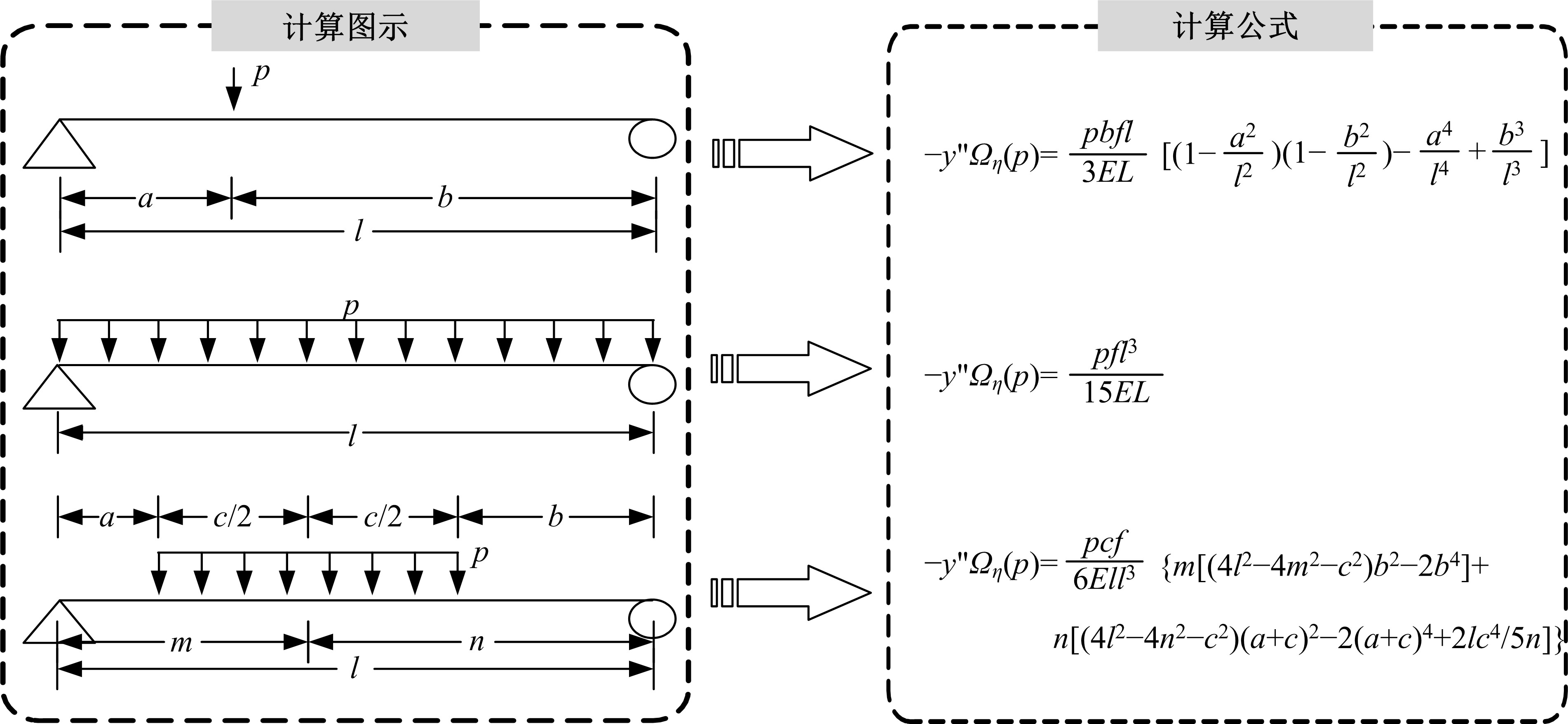
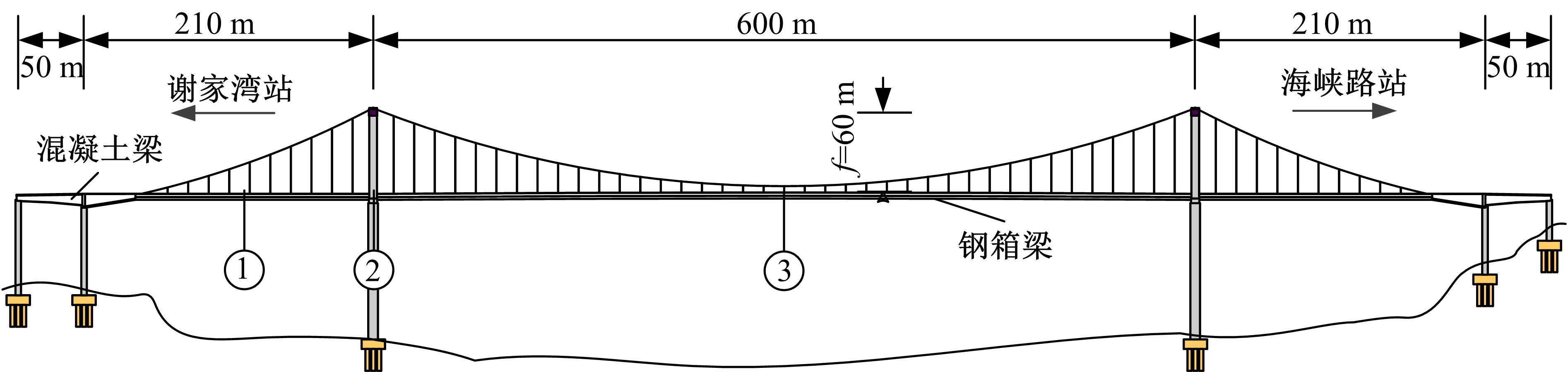
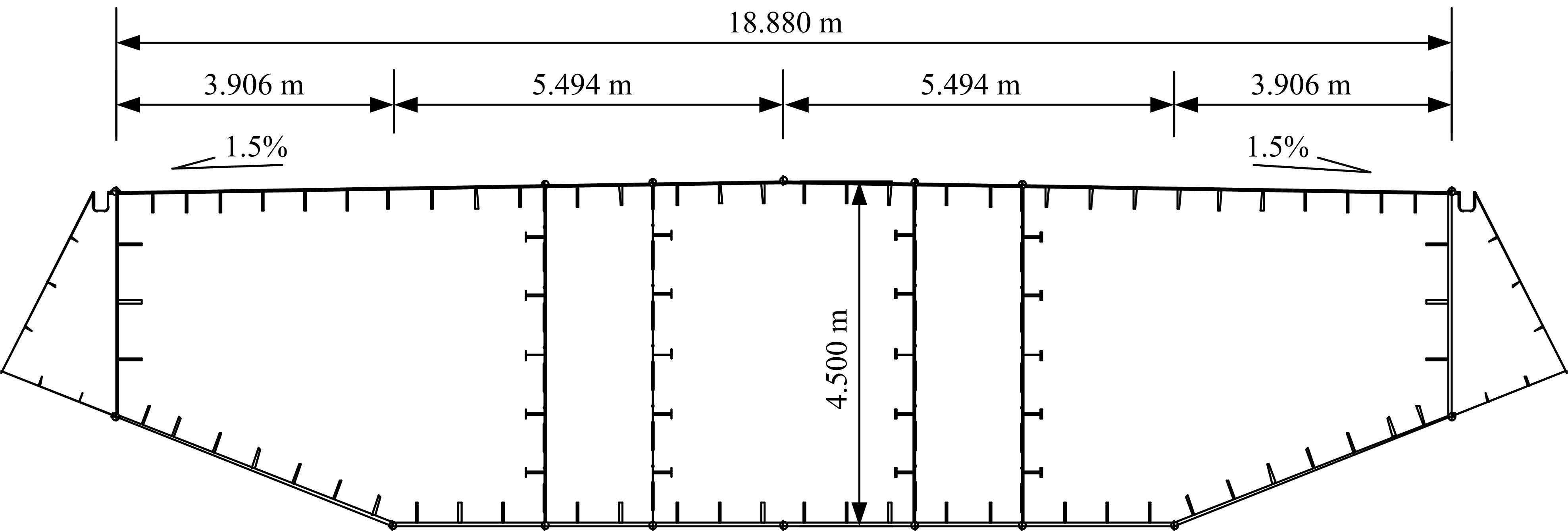
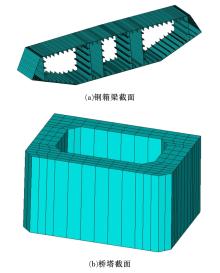
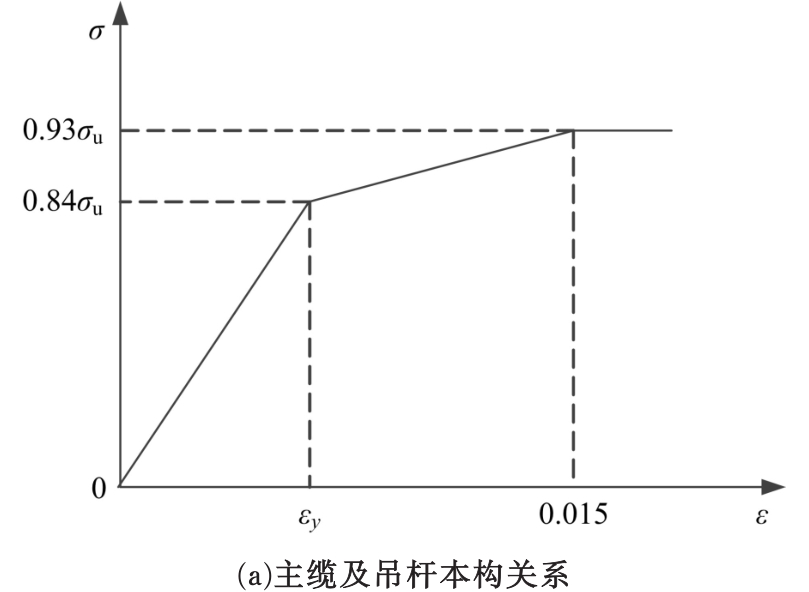
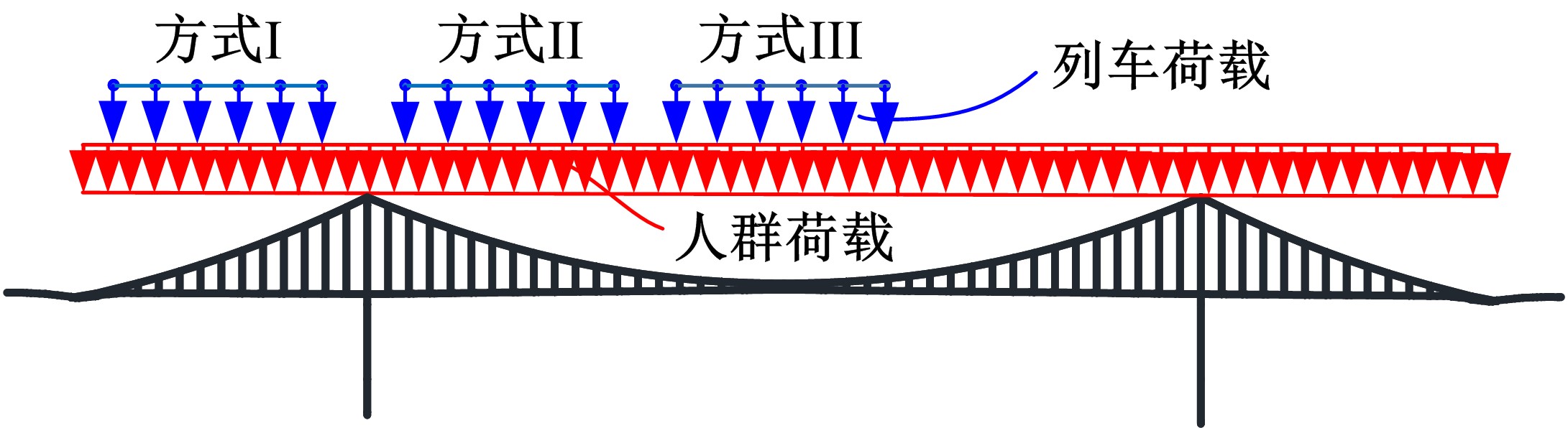
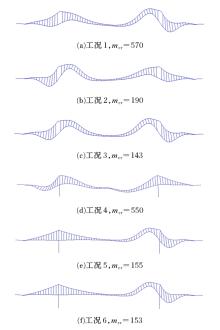
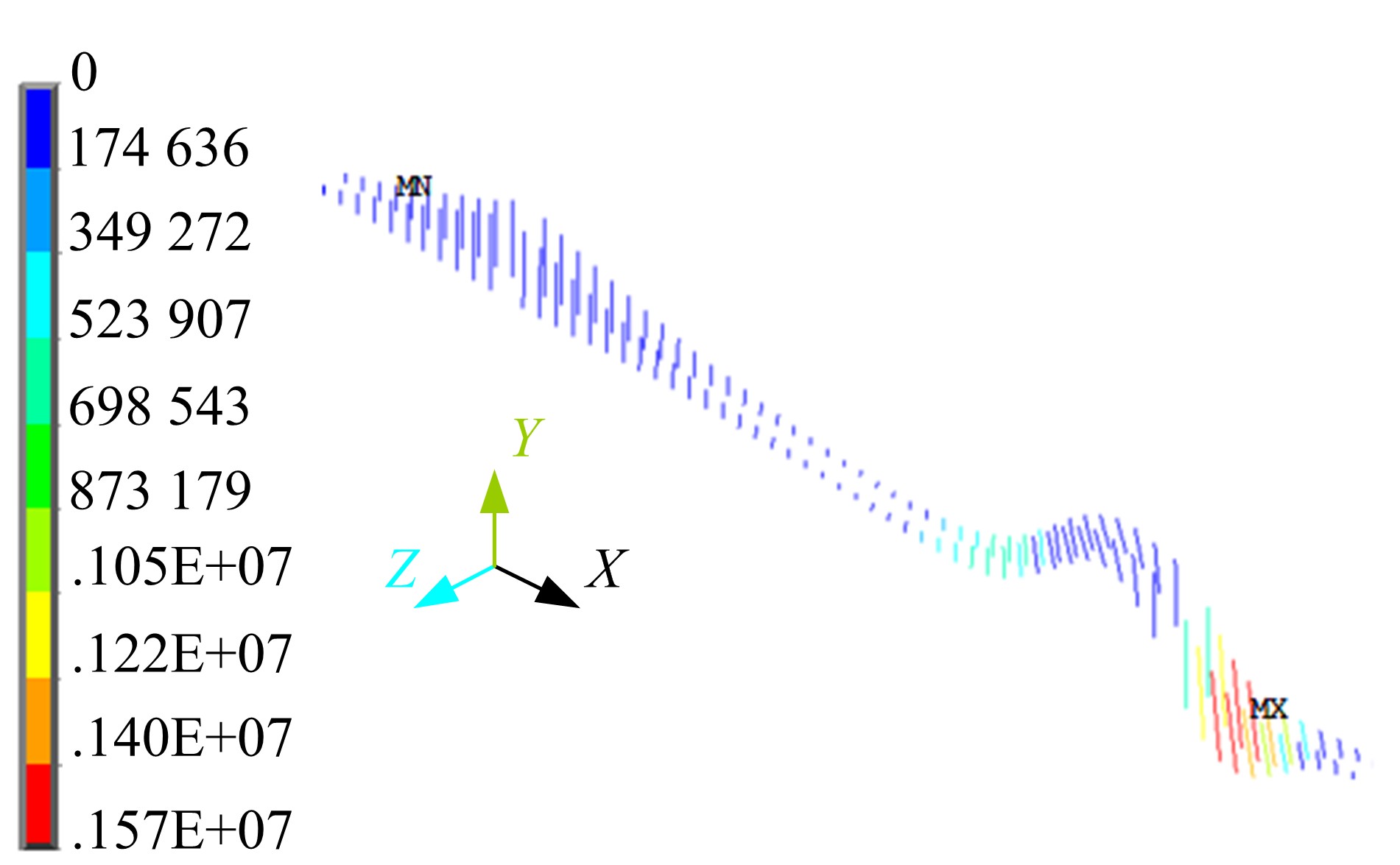
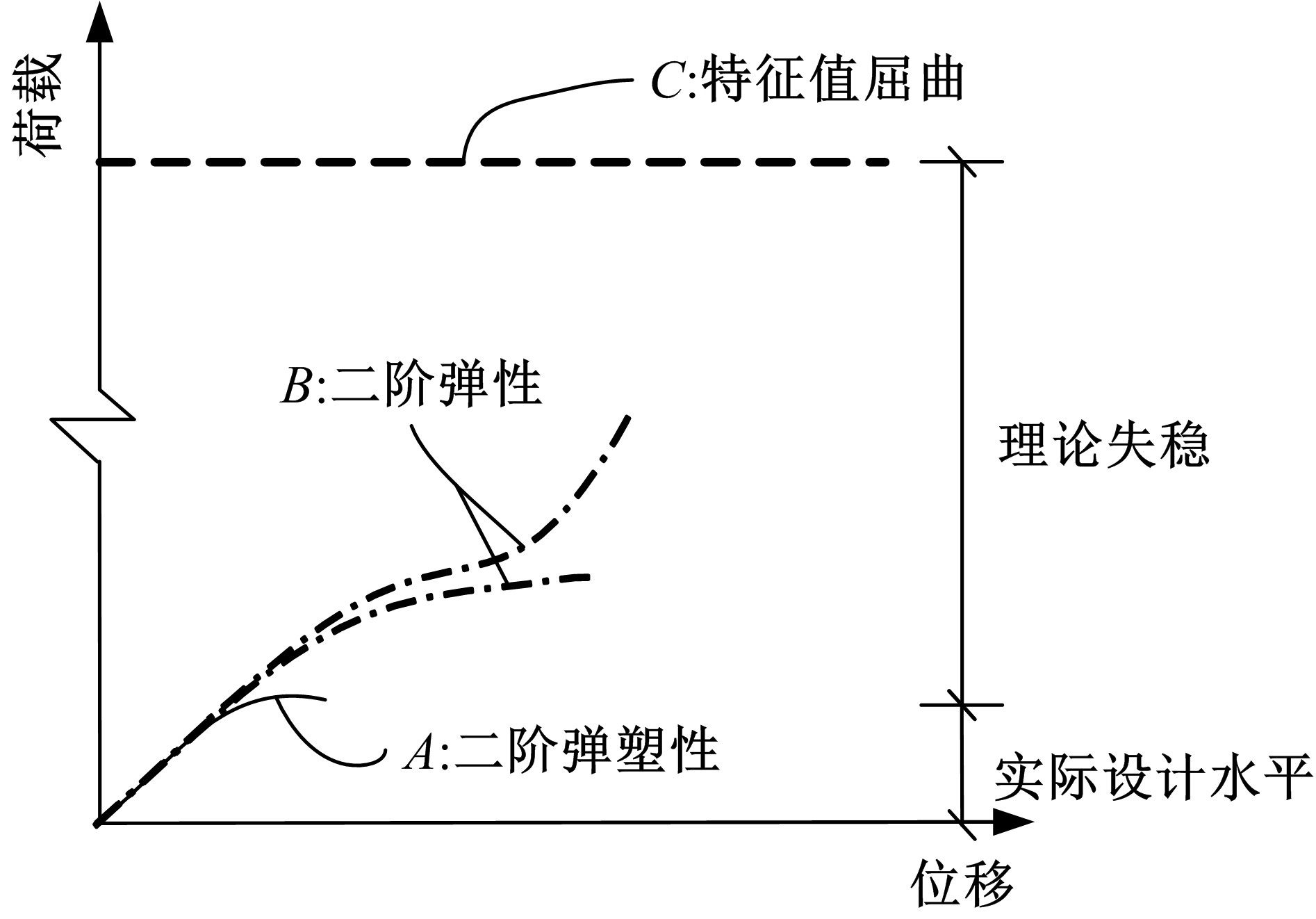
为完善自锚式悬索桥面内稳定性理论，首先通过结构稳定性的概念初步判定该桥型不存在面内分岔失稳的可能性；进而在自锚式悬索桥挠度方程中通过引入位移干扰量，以幂级数干扰位移形式反证其不会出现面内弹性分岔失稳；最后以实桥为例，通过数值模型按弹性及弹塑性稳定理论计算分析了桥梁的荷载系数、破坏模式等。结果表明：在挠度理论适用范围内，自锚式悬索桥不存在面内分岔失稳；数值分析结果显示该实桥面内分岔失稳由吊索断裂引起，超出挠度理论应用范围，而极限承载力能满足安全性要求。

关键词: 桥梁工程, 自锚式悬索桥稳定理论, 数值分析方法, 主缆-吊索-主梁闭合传力路径, 挠度理论, 分岔失稳

Abstract:

In order to consummate the in-plane stability theory of self-anchored suspension bridge, firstly it is preliminarily determined that the bifurcation failure mode of this type bridge can not occur through the concept of structural stability. Furthermore, by introducing the displacement interference which is assumed as power series form in the deflection equation of the self-anchored suspension bridge, it is proved that the elastic bifurcation instability will not occur. Finally, a practical bridge is taken as an example, the numerical models according to the elastic stability and elastic-plastic stability theory are calculated and analyzed to obtain the load coefficient, bridge failure modes etc.. The results show that there is no in-plane bifurcation failure mode for self-anchored suspension bridge in the scope of application of deflection theory. Numerical analysis shows that the bifurcation instability in the actual bridge deck is caused by the breakage of the sling, which exceeds the application range of deflection theory, and the ultimate bearing capacity satisfies the safety requirements.

Key words: bridge engineering, self-anchored suspension bridge stability theory, numerical analysis method, cable-sling-girder closed transmission path, deflection theory, bifurcation instability

中图分类号:

U448.25

白伦华,沈锐利,张兴标,王路. 自锚式悬索桥的面内稳定性[J]. 吉林大学学报(工学版), 2019, 49(5): 1500-1508.

Lun-hua BAI,Rui-li SHEN,Xing-biao ZHANG,Lu WANG. In-plane stability of self-anchored suspension bridge[J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(5): 1500-1508.

图/表 14

图1

图2

图3

图4

图5

图6

图7

图8

表1

图9

图10

图11

表2

图12

参考文献 15

1	Nie Jian-guo , Zhou Meng , Wang Yu-hang , et al . Cable anchorage system modeling methods for self-anchored suspension bridges with steel box girders[J]. Journal of Bridge Engineering, 2014, 19(2): 172-185.
2	王邵锐, 周志祥, 高燕梅, 等 . 考虑缆-梁联合作用的自锚式悬索桥恒载状态计算方法研究［J］. 土木工程学报, 2015, 48(8): 70-76.
	Wang Shao-rui , Zhou Zhi-xiang , Gao Yan-mei , et al . Study on the calculation method of the dead load state for the self-anchored suspension bridge considering the joint action of cable-stiffening girder[J]. China Civil Engineering Journal, 2015, 48(8): 70-76.
3	李建慧, 李爱群 . 自锚式悬索桥静力随机分析与可靠度评估［J］. 中国公路学报, 2012, 25(6): 74-79.
	Li Jian-hui , Li Ai-qun . Stochastic analysis of static charateristics and reliability assessment for self-anchored suspension bridge[J]. China Journal of Highway and Transport, 2012, 25(6): 74-79.
4	王保群, 张强勇, 张凯, 等 . 自锚式斜拉-悬吊协作体系桥梁动力性能［J］. 吉林大学学报: 工学版, 2009, 39(3): 686-690.
	Wang Bao-qun , Zhang Qiang-yong , Zhang Kai , et al . Dynamic characteristics for self-anchored cable-stayed suspension bridges[J]. Journal of Jilin University (Engineering and Technology Edition), 2009, 39(3): 686-690.
5	沈锐利, 齐东春, 唐茂林 . 杭州江东大桥静力特性全桥模型试验研究［J］. 土木工程学报, 2011, 44(1): 74-80.
	Shen Rui-li , Qi Dong-chun , Tang Mao-lin . Model test study of the static property of the Jiangdong Bridge in Hangzhou[J]. China Civil Engineering Journal, 2011, 44(1): 74-80.
6	胡建华, 沈锐利, 张贵明, 等 . 佛山平胜大桥全桥模型试验研究[J]. 土木工程学报, 2007, 40(5): 17-25.
	Hu Jian-hua , Shen Rui-li , Zhang Gui-ming , et al . Total bridge model study of the Pingsheng Bridge in Foshan[J]. China Civil Engineering Journal, 2007, 40(5): 17-25.
7	王桢, 吴海军, 周志祥, 等 . 大跨径自锚式悬索桥吊索索力相邻影响分析［J］. 土木工程学报, 2016, 49(6): 51-60.
	Wang Zhen , Wu Hai-jun , Zhou Zhi-xiang , et al . Analysis on near influence of cable force in large-span self-anchored suspension bridges[J]. China Civil Engineering Journal, 2016, 49(6): 51-60.
8	胡建华, 王连华, 沈锐利, 等 . 大跨度自锚式悬索桥稳定性研究［J］. 湖南大学学报：自然科学版, 2008, 35(7): 12-15.
	Hu Jian-Hua , Wang Lian-hua , Shen Rui-li , et al . Research on the stability of long span self-anchored suspension bridges[J]. Journal of Hunan University (Natural Sciences), 2008, 35(7): 12-15.
9	Jung M R , Shin S U , Attard M M , et al . Deflection theory for self-anchored suspension bridges under live load[J]. Journal of Bridge Engineering, 2014, 20(7): 1-19.
10	Jung M R , Jang M J , Attard M M , et al . Elastic stability behavior of self-anchored suspension bridges by the deflection theory[J]. International Journal of Structural Stability & Dynamics, 2017, 17(4): 1-23.
11	李立峰, 程翔云 . 代换梁法在自锚式悬索桥上的推广应用［J］. 工程力学, 2008, 25(8): 212-217.
	Li Li-feng , Cheng Xiang-yun . Extensional application of substitutional beam method to self-anchored suspension bridge[J]. Engineering Mechanics, 2008, 25(8): 212-217.
12	赵维贺 . 新型自锚式悬索桥的稳定性及极限承载力分析［D］. 大连：大连理工大学土木工程学院, 2007.
	Zhao Wei-he . The buckle and ultimate bearing capacity analysis for a new style self-anchored suspension bridge[D]. Dalian: School of Civil Engieering, Dalian University of Technology, 2007.
13	铁道第三勘察设计院 . 铁路桥涵设计基本规范［M］. 2版. 北京：中国铁道出版社, 2005.
14	重庆交通科研设计院 . 公路斜拉桥设计细则(JTG/T D65-01-2007)［M］. 北京：人民交通出版社， 2007.
15	沈锐利, 成新, 白伦华, 等 . 自锚式悬索桥极限承载力及安全性评价方法研究［J］. 铁道学报, 2017, 39(11): 89-96.
	Shen Rui-li , Cheng Xin , Bai Lun-hua , et al . Study on static ultimate bearing capacity and safety evaluation method of self-anchored suspension bridges[J]. Journal of the China Railway Society, 2017， 39(11): 89-96.

相关文章 15

[1]	万世成,黄侨,关健,郭赵元. 预应力碳纤维板加固钢⁃混凝土组合连续梁负弯矩区试验[J]. 吉林大学学报(工学版), 2019, 49(4): 1114-1123.
[2]	赵金钢,张明,占玉林,谢明志. 基于塑性应变能密度的钢筋混凝土墩柱损伤准则[J]. 吉林大学学报(工学版), 2019, 49(4): 1124-1133.
[3]	李万恒,申林,王少鹏,赵尚传. 基于多阶段分区域动力测试的桥梁结构损伤评估[J]. 吉林大学学报(工学版), 2019, 49(3): 773-780.
[4]	惠迎新,毛明杰,刘海峰,张尚荣. 跨断层桥梁结构地震响应影响[J]. 吉林大学学报(工学版), 2018, 48(6): 1725-1734.
[5]	郑一峰, 赵群, 暴伟, 李壮, 于笑非. 大跨径刚构连续梁桥悬臂施工阶段抗风性能[J]. 吉林大学学报(工学版), 2018, 48(2): 466-472.
[6]	宫亚峰, 何钰龙, 谭国金, 申杨凡. 三跨独柱连续曲线梁桥抗倾覆稳定性分析[J]. 吉林大学学报(工学版), 2018, 48(1): 133-140.
[7]	魏志刚, 刘寒冰, 时成林, 宫亚峰. 考虑桥面铺装作用的简支梁桥横向分布系数计算[J]. 吉林大学学报(工学版), 2018, 48(1): 105-112.
[8]	魏志刚, 时成林, 刘寒冰, 张云龙. 车辆作用下钢-混凝土组合简支梁动力特性[J]. 吉林大学学报(工学版), 2017, 47(6): 1744-1752.
[9]	张云龙, 刘占莹, 吴春利, 王静. 钢-混凝土组合梁静动力响应[J]. 吉林大学学报(工学版), 2017, 47(3): 789-795.
[10]	刘寒冰, 时成林, 谭国金. 考虑剪切滑移效应的叠合梁有限元解[J]. 吉林大学学报(工学版), 2016, 46(3): 792-797.
[11]	谭国金, 刘子煜, 魏海斌, 王龙林. 偏心直线预应力筋简支梁自振频率计算方法[J]. 吉林大学学报(工学版), 2016, 46(3): 798-803.
[12]	曹珊珊, 雷俊卿. 考虑区间不确定性的钢结构疲劳寿命分析[J]. 吉林大学学报(工学版), 2016, 46(3): 804-810.
[13]	肖赟, 雷俊卿, 张坤, 李忠三. 多级变幅疲劳荷载下预应力混凝土梁刚度退化[J]. 吉林大学学报(工学版), 2013, 43(03): 665-670.
[14]	焦常科, 李爱群, 伍小平. 大跨双层斜拉桥多点激励地震响应[J]. , 2012, 42(04): 910-917.
[15]	刘寒冰, 郑继光, 邹品德. 叠合式钢筋混凝土圆截面短柱偏心受压承载力计算[J]. 吉林大学学报(工学版), 2011, 41(增刊2): 159-163.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

工况号	列车布载方式	桥塔效应
1	1	不考虑
2	2	不考虑
3	3	不考虑
4	1	考虑
5	2	考虑
6	3	考虑

工况号	活载布载方式	荷载模式	最大荷载倍数
7	截面①轴力最不利	活载单独放大	10.08
8	截面①正弯矩最不利		11.79
9	截面②轴力最不利		10.14
10	截面②负弯矩最不利		9.01
11	截面③轴力最不利		10.13
12	截面③正弯矩最不利		10.02
7a	截面①轴力最不利	恒载活载同比放大	2.21
8a	截面①正弯矩最不利		2.17
9a	截面②轴力最不利		2.21
10a	截面②负弯矩最不利		1.98
11a	截面③轴力最不利		2.27
12a	截面③正弯矩最不利		2.59