吉林大学学报(工学版) ›› 2025, Vol. 55 ›› Issue (2): 664-672.doi: 10.13229/j.cnki.jdxbgxb.20230086
• 交通运输工程·土木工程 • 上一篇
变截面两铰拱推力影响线解析解及损伤识别应用
- 1.兰州交通大学 土木工程学院,兰州 730070
2.安徽建筑大学 土木工程学院,合肥 230601
3.安徽建筑大学 建筑健康监测与灾害预防技术国家地方联合工程实验室,合肥 230601
Analytical solution of thrust influence line of variable section two-hinged arch and application of damage identification
Yu ZHOU1,2,3( ),Meng LI2,3,Sheng-kui DI1,Xian-zeng SHI2,Dong CHEN2
),Meng LI2,3,Sheng-kui DI1,Xian-zeng SHI2,Dong CHEN2
- 1.School of Civil Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China
2.School of Civil Engineering,Anhui Jianzhu University,Hefei 230601,China
3.National and Local Joint Engineering Laboratory of Building Health Monitoring and Disaster Prevention Technology,Anhui Jianzhu University,Hefei 230601,China
摘要:
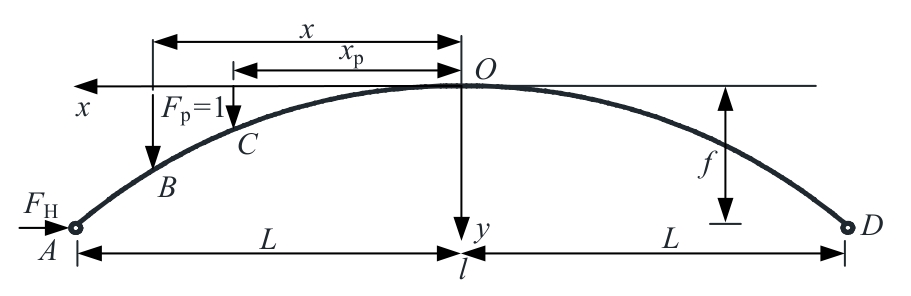
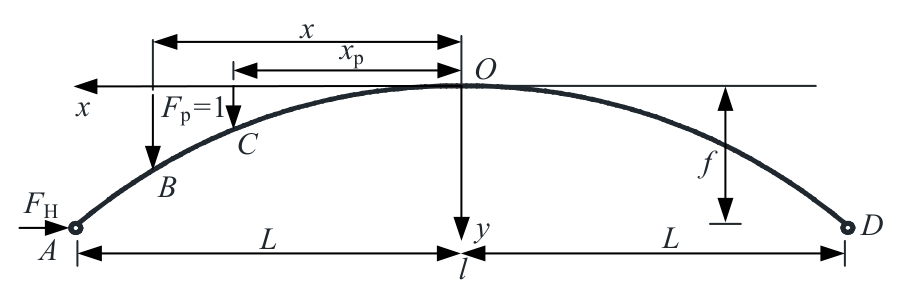
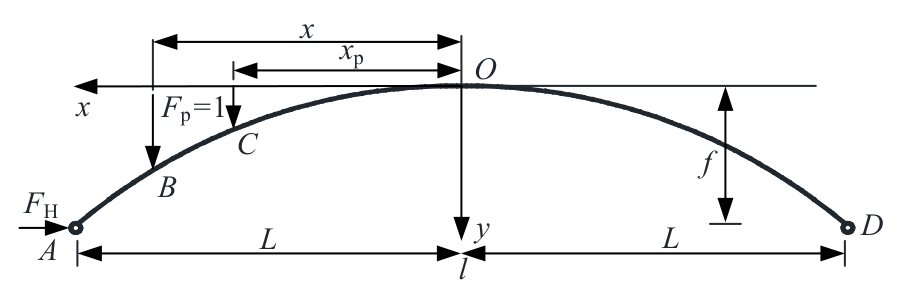
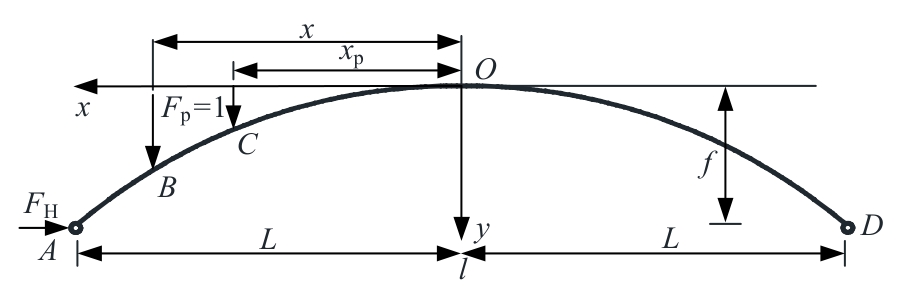
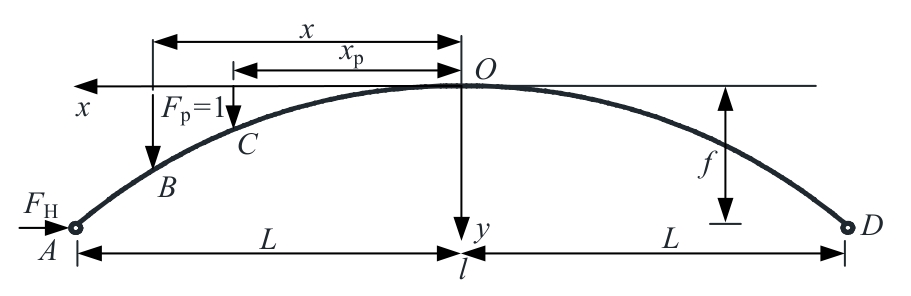
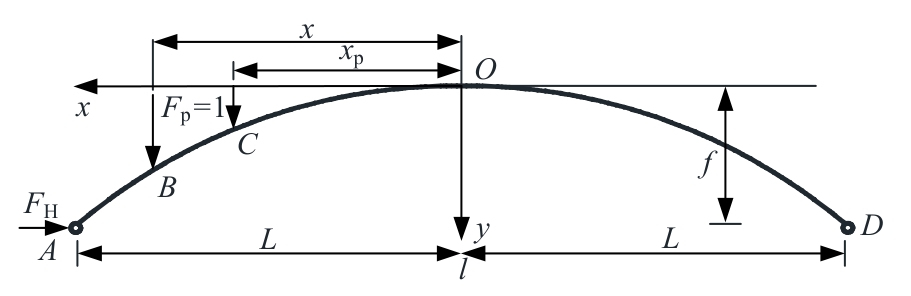
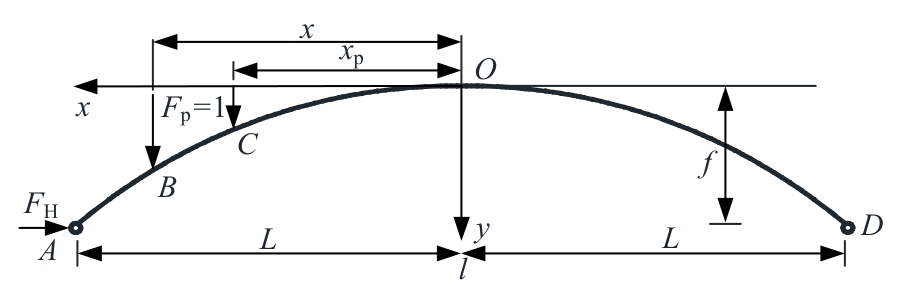
针对变截面两铰拱水平推力影响线解析研究仍不完善的现状,围绕变截面两铰拱在抛物线、悬链线两种线型下的推力影响线解析解推导与应用展开研究,利用Ritter公式确立拱圈截面变化规律,对变截面两铰拱进行曲线积分,基于力法原理提出两种线型的变截面两铰拱水平推力影响线解析解,进而提取损伤前后两铰拱结构推力影响线差值曲率损伤识别指标,提出基于推力影响线的变截面两铰拱损伤识别新方法,对比有限元结果表明:推力影响线解析解与有限元计算偏差在8.5%以内,通过有限元算例验证了本文方法可以实现两铰拱结构损伤定位,可作为拱结构在移动荷载作用下的拱座基础强度设计依据与拱桥快速检测应用理论参考。
中图分类号:
- TU311
| 1 | Cocchetti G, Rizzi E. Least-thickness symmetric circular masonry arch of maximum horizontal thrust[J]. Archive of Applied Mechanics, 2021, 91(6): 2617-2639. |
| 2 | 蒋伟, 吕大刚. 混凝土两铰圆弧拱的面内徐变稳定性[J]. 工程力学, 2012, 29(2): 186-189. |
| Jiang Wei, Da-gang Lyu. In-plane creep buckling of pin-ended concrete circle arches[J]. Engineering Mechanics, 2012, 29(2): 186-189. | |
| 3 | 谢旭, 李辉, 黄剑源. 大跨度两铰钢拱桥面内稳定分析[J]. 土木工程学报, 2004, 37(8): 43-49. |
| Xie Xu, Li Hui, Huang Jian-yuan. Study on in-plane stability of long-span two-hingedsteelarchbridges[J]. China Civil Engineering Journal, 2004, 37(8): 43-49. | |
| 4 | 周宇, 狄生奎, 李喜梅, 等. 基于弹性约束梁应变影响线曲率的桥梁结构损伤识别[J]. 应用基础与工程科学学报, 2021, 29(4): 901-914. |
| Zhou Yu, Di Sheng-kui, Li Xi-mei, et al. Damage identification of bridge structural based on strain influence line curvature of elastic restrained beam[J]. Journal of Basic Science and Engineering, 2021, 29(4): 901-914. | |
| 5 | 王宁波, 左晴, 李靖, 等. 基于当前多影响线信息的超静定梁损伤识别方法[J]. 中南大学学报:自然科学版, 2021, 52(9): 3284-3294. |
| Wang Ning-bo, Zuo Qing, Li Jing, et al. Damage detection method for statically indeterminate bridge based on multi-influence line information in current state[J]. Journal of Central South University (Science and Technology), 2021, 52(9): 3284-3294. | |
| 6 | 贺文宇, 武骥元, 任伟新. 基于车致桥梁响应和L1正则化的损伤识别研究[J]. 中国公路学报, 2021, 34(4): 61-70. |
| He Wen-yu, Wu Ji-yuan, Ren Wei-xin. Bridge damage detection based on the moving-vehicle-induced response and L1 regularization[J]. China Journal of Highway and Transport, 2021, 34(4): 61-70. | |
| 7 | Zheng X, Yi T H, Yang D H, et al. Stiffness estimation of girder bridges using influence lines identified from vehicle-induced structural responses[J]. Journal of Engineering Mechanics-ASCE, 2021, 147(8): 4021042. |
| 8 | 周宇, 狄生奎, 项长生, 等. 基于弹性约束支承梁转角影响线的梁结构损伤诊断[J]. 浙江大学学报: 工学版, 2020, 54(5): 879-888. |
| Zhou Yu, Di Sheng-kui, Xiang Chang-sheng, et al. Beam structure damage detection based on rotational-angleinfluence-lines of elastic-constrained-support beam[J]. Journal of Zhejiang University (Engineering Science), 2020, 54(5): 879-888. | |
| 9 | Zheng X, Yi T H, Zhong J W, et al. Rapid evaluation of load-carrying capacity of long-span bridges using limited testing vehicles[J]. Journal of Bridge Engineering, 2022, 27(4): 0001838. |
| 10 | Wang N B, Shen W, Guo C R, et al. Moving load test-based rapid bridge capacity evaluation through actual influence line[J]. Engineering Structures, 2022, 252: 113630. |
| 11 | 王立宪, 周宇, 狄生奎, 等. 考虑边界非理想的铁路桥梁挠度影响线分析与损伤识别[J]. 工程科学与技术, 2020, 52(3): 123-132. |
| Wang Li-xian, Zhou Yu, Di Sheng-kui, et al. Influence line analysis and damage detection of railway bridgedeflection with non-ideal boundaries[J]. Advanced Engineering Sciences, 2020, 52(3): 123-132. | |
| 12 | 胡常福, 雷亮亮, 陈海龙, 等. 等截面抛物线拱桥内力实用解析解研究[J]. 铁道科学与工程学报, 2011, 8(5): 12-18. |
| Hu Chang-fu, Lei Liang-liang, Chen Hai-long, et al. Research on practical analytic solution of parabolic arch bridges with uniform section[J]. Journal of Railway Science and Engineering, 2011, 8(5): 12-18. | |
| 13 | 杨雨厚, 刘来君, 孙维刚, 等. 等截面抛物线无铰拱挠度影响线实用解析解[J]. 计算力学学报, 2017, 34(4): 480-486. |
| Yang Yu-hou, Liu Lai-jun, Sun Wei-gang,et al. Practical analytical solution of deflection influence line of clamped parabolic arch bridges with uniform section[J]. Chinese Journal of Computational Mechanics, 2017, 34(4): 480-486. | |
| 14 | 周宇, 许成超, 赵青, 等. 变截面悬链线无铰拱应变影响线的解析解[J]. 计算力学学报, 2022, 39(5): 551-556. |
| Zhou Yu, Xu Cheng-chao, Zhao Qing,et al. Practical analytical expression to strain influence line of varying cross section catenary fixed arch[J]. Chinese Journal of Computational Mechanics, 2022, 39(5): 551-556. | |
| 15 | 胡常福, 陆小雨, 甘慧慧, 等. 基于近似积分的悬链线拱实用解析解[J]. 中南大学学报: 自然科学版, 2015, 46(3): 1058-1065. |
| Hu Chang-fu, Lu Xiao-yu, Gan Hui-hui,et al. Practical analytical solution of catenary arch based on approximate integration method[J]. Journal of Central South University (Science and Technology), 2015, 46(3): 1058-1065. | |
| 16 | 胡常福, 何兵兵, 石萃佳, 等. 复杂轴线拱结构实用解析解研究[J]. 中南大学学报: 自然科学版, 2018, 49(1): 217-225. |
| Hu Chang-fu, He Bing-bing, Shi Cui-jia,et al. Research on approximate analytical solution of arch structure with complex arch axis[J]. Journal of Central South University (Science and Technology), 2018, 49(1): 217-225. |
| [1] | 姜浩,赵正文. 玄武岩纤维网格水泥基复合材料加固RC梁抗剪性能试验[J]. 吉林大学学报(工学版), 2025, 55(1): 211-220. |
| [2] | 王羽岱,王斌,苗福生,马楠. 水热耦合变化下衬砌渠道冻胀响应[J]. 吉林大学学报(工学版), 2025, 55(1): 256-268. |
| [3] | 韦芳芳,李丽萍,徐庆鹏,赵有正,杨晶晶. 受火双钢板-混凝土组合剪力墙加固后抗震性能试验[J]. 吉林大学学报(工学版), 2025, 55(1): 230-244. |
| [4] | 杨伟松,张安,许卫晓,李海生,杜轲. 刚度增强型金属连梁阻尼器的抗震性能[J]. 吉林大学学报(工学版), 2024, 54(9): 2469-2483. |
| [5] | 赵金全,周龙,丁永刚,朱熔基. 螺旋箍筋-波纹管浆锚连接锚固性能试验[J]. 吉林大学学报(工学版), 2024, 54(9): 2484-2494. |
| [6] | 阎奇武,邹忠亮. 减震结构阻尼器优化布置混合算法[J]. 吉林大学学报(工学版), 2024, 54(8): 2267-2274. |
| [7] | 姜封国,周玉明,白丽丽,梁爽. 改进磷虾群算法及其在结构优化中的应用[J]. 吉林大学学报(工学版), 2024, 54(8): 2256-2266. |
| [8] | 张广泰,周乘孝,刘诗拓. 盐渍土环境下纤维锂渣混凝土柱恢复力模型[J]. 吉林大学学报(工学版), 2024, 54(7): 1944-1957. |
| [9] | 刁延松,任义建,杨元强,赵凌云,刘秀丽,刘芸. 带有摩擦耗能组件的可更换钢梁柱拼接节点抗震性能试验[J]. 吉林大学学报(工学版), 2024, 54(6): 1643-1656. |
| [10] | 樊学平,刘月飞. 基于改进高斯混合粒子滤波新算法的桥梁极值应力动态预测[J]. 吉林大学学报(工学版), 2024, 54(4): 1038-1044. |
| [11] | 刘一凡,缪志伟,申晨,耿祥东. 基于蒙特卡罗法的不均匀锈蚀钢筋力学性能评估[J]. 吉林大学学报(工学版), 2024, 54(4): 1007-1015. |
| [12] | 樊学平,周衡,刘月飞. 基于Gaussian Copula-贝叶斯动态模型的桥梁构件时变可靠性分析[J]. 吉林大学学报(工学版), 2024, 54(2): 485-493. |
| [13] | 杨海旭,郭悦,王海飙,胡宜. 冷弯薄壁型钢-胶合木组合梁受弯性能[J]. 吉林大学学报(工学版), 2024, 54(12): 3513-3525. |
| [14] | 范亮,徐英铭,谭阳. 集束群钉式装配组合梁界面滑移计算[J]. 吉林大学学报(工学版), 2023, 53(9): 2533-2541. |
| [15] | 樊学平,周衡,刘月飞. 桥梁时变可靠性的多过程贝叶斯动态混合预测[J]. 吉林大学学报(工学版), 2023, 53(8): 2332-2338. |
|
||