改进磷虾群算法及其在结构优化中的应用

doi:10.13229/j.cnki.jdxbgxb.20221349

摘要/Abstract

摘要：

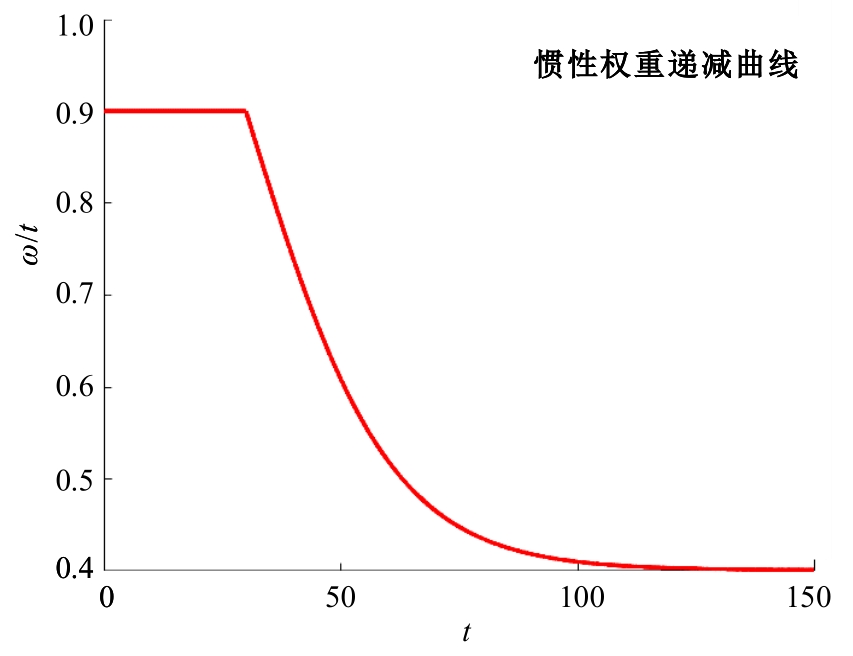
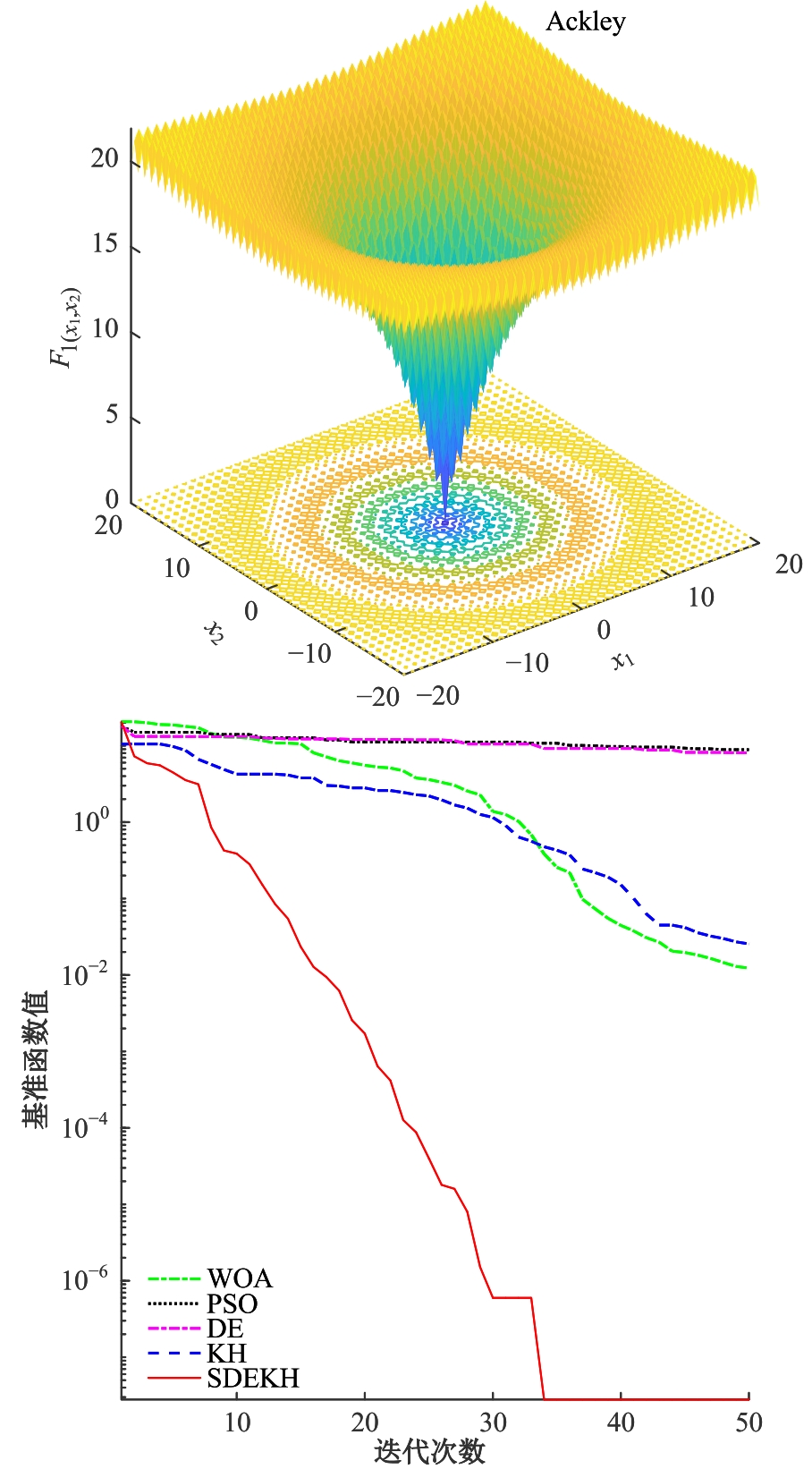
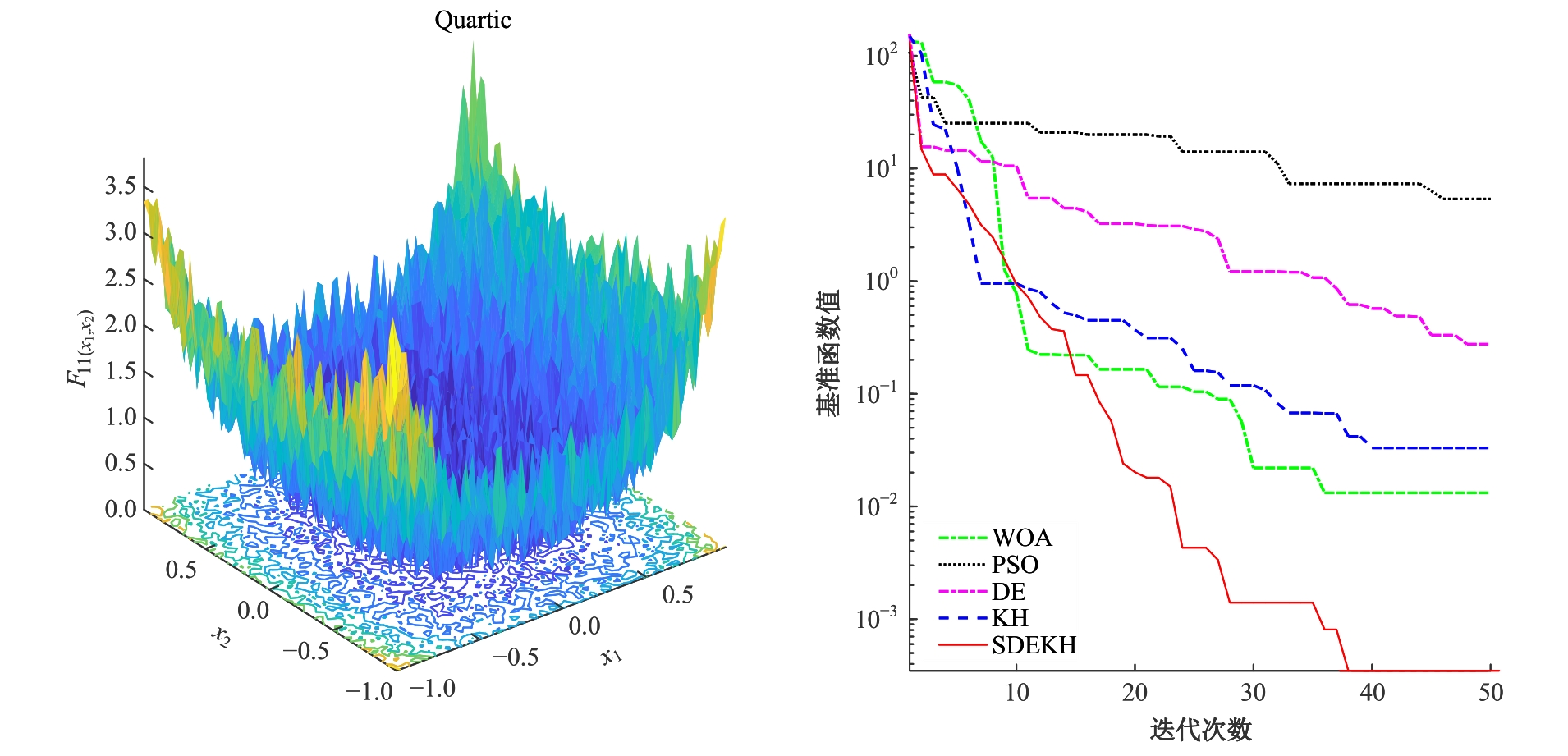
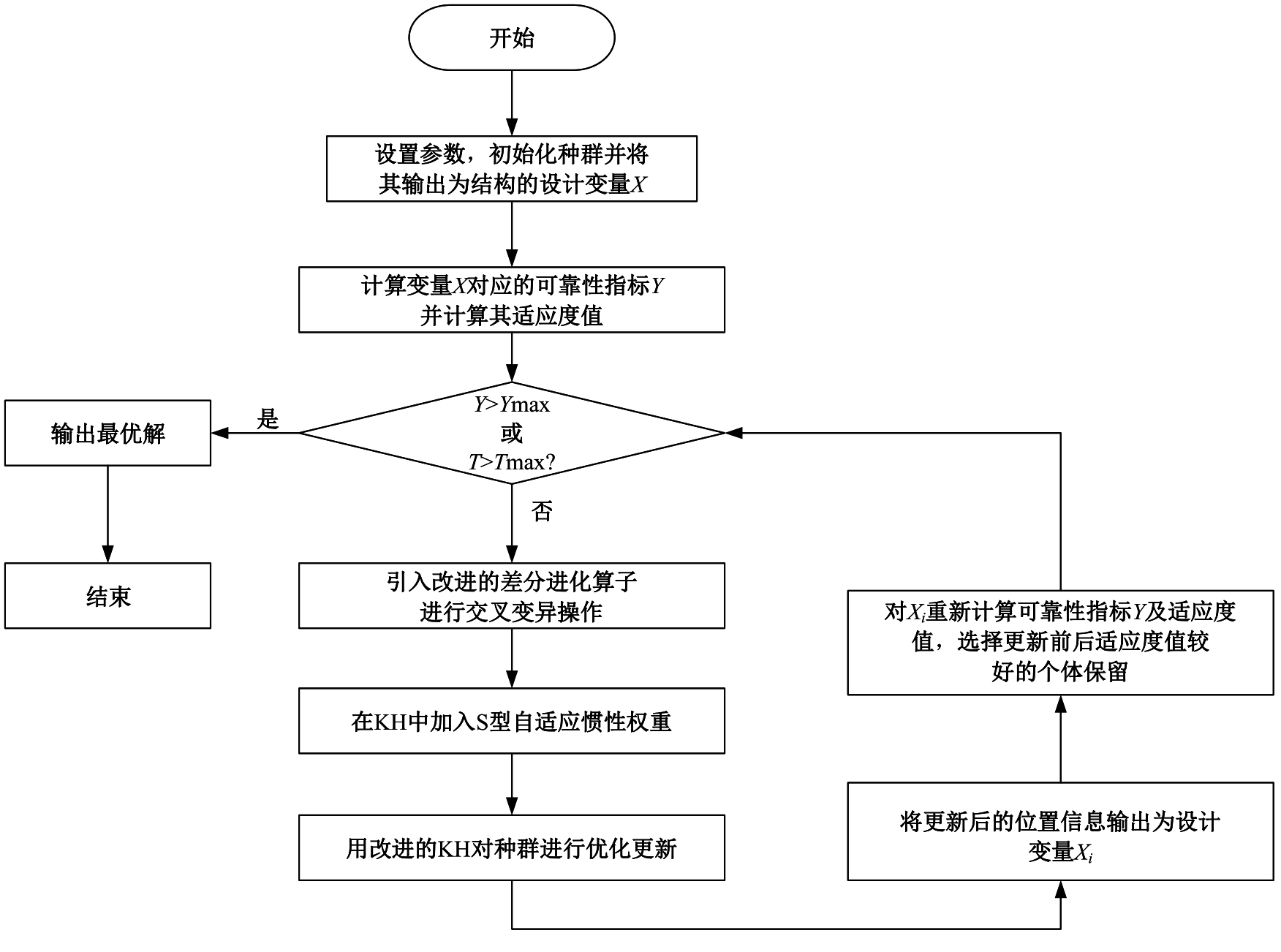
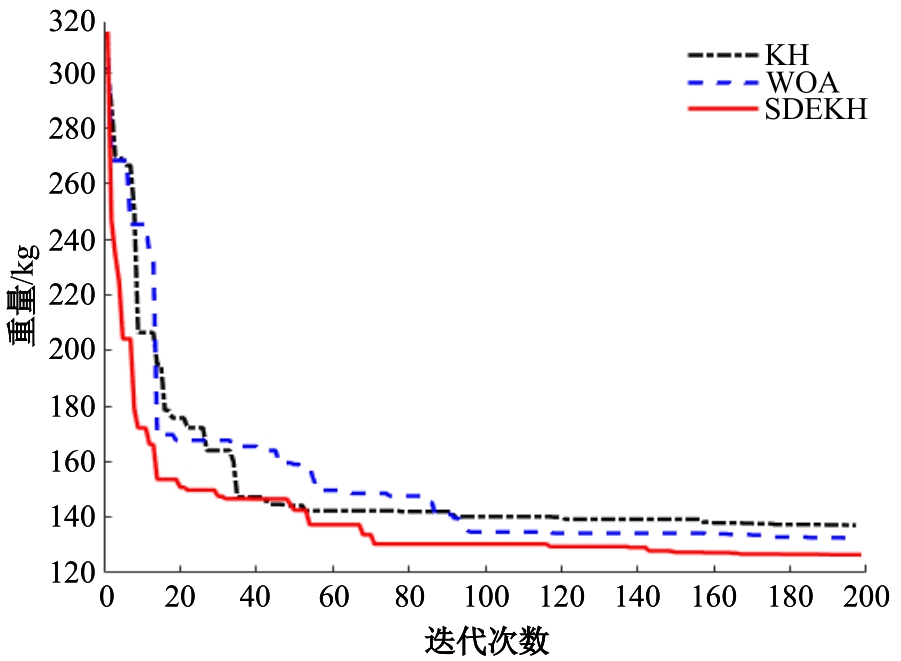
本文针对标准磷虾群算法（KH）存在收敛速度较慢、计算精度不够和对复杂问题易陷入局部最优解的缺陷做出改进与完善，提出一种融合改进差分进化算子和S型自适应惯性权重的改进磷虾群算法（SDEKH）。通过多种标准测试函数对SDEKH、KH等智能算法进行对比测试，验证了SDEKH的优良性能；并运用SDEKH对桁架结构进行优化设计，通过与其他方法的优化结果对比验证了SDEKH的优化效率和精度均有提升，为工程结构优化设计提供了一种更加高效、精准的方法。

关键词: 结构工程, 改进磷虾群算法, 差分进化算子, 惯性权重, 结构优化

Abstract:

In this paper， the standard krill algorithm （KH） has the disadvantages of slow convergence speed， insufficient calculation accuracy and easy to fall into local optimal solution for complex problems， an improved krill algorithm （SDEKH） which combines improved differential evolution operator and S-type adaptive inertia weight is proposed in this paper. Through a variety of standard test functions to compare and test a variety of intelligent algorithms such as SDEKH and KH， the excellent performance of SDEKH is verified， and SDEKH is used to optimize the truss structure， and the optimization results of SDEKH are compared with other methods to verify that the optimization efficiency and accuracy are improved， which provides a more efficient and accurate method for engineering structure optimization design.

Key words: structural engineering, improved krill algorithm, differential evolution operator, inertia weight, structural optimization

中图分类号:

TU323.4

姜封国,周玉明,白丽丽,梁爽. 改进磷虾群算法及其在结构优化中的应用[J]. 吉林大学学报(工学版), 2024, 54(8): 2256-2266.

Feng-guo JIANG,Yu-ming ZHOU,Li-li BAI,Shuang LIANG. Improved krill algorithm and its application in structural optimization[J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(8): 2256-2266.

图/表 19

图1

表1

标准测试函数"

序号	函数名称	函数表达式
1	Ackley	$F 1 (x) = - 20 e x p (- 0.2 1 n ∑ i = 1 n x i 2) - e x p (1 n ∑ i = 1 n c o s 2 π x i)) + 20 + e$
2	Rastrigin	$F 2 (x) = 10 ? n + ∑ i = 1 n (x i 2 - 10 ? c o s (2 π x i))$
3	Schwefel 1	$F 3 (x) = ∑ i = 1 n (∑ j = 1 i x j) 2$
4	Schwefel 2	$F 4 (x) = m a x {x i, 1 ≤ i ≤ n}$
5	Schwefel	$F 5 (x) = ∑ i = 1 n - x i s i n (x i) + 418.982 ? 9 × 5$
6	Step	$F 6 (x) = ∑ i = 1 n ([x i + 0.5]) 2$
7	Penalty	$F 7 (x) = π n (10 ? s i n (π y 1) + ∑ i = 1 n u (x i, 10,100,4) + (y n - 1) 2 + ∑ i = 1 n - 1 (y i - 1) 2 (1 + 10 s i n 2 (π y i + 1)))$
8	Rosebrock	$F 8 (x) = ∑ i = 1 n - 1 100 x i + 1 - x i 2) 2 + (x i - 1) 2]$
9	Griewank	$F 9 (x) = 1 4 ? 000 ∑ i = 1 n x i 2 - ∏ i n c o s (x i i) + 1$
10	Sphere	$F 10 (x) = ∑ i = 1 n x i 2$
11	Quartic	$F 11 (x) = ∑ i = 1 n i x i 4 + r a n d$

表1

图2

图3

图4

表2

测试函数测试结果对比"

函数	SDEKH			KH			WOA	PSO	DE
函数	最优值	平均值	标准差	最优值	平均值	标准差	最优值	最优值	最优值
$F 1$	2.472 1E^-08	2.236 2E^-04	3.938 9E^-04	0.050 2	2.006 4	0.885 3	0.008 5	9.967 1	8.856 1
$F 2$	5.066 3E^-08	1.248 6E^-04	4.475 1E^-04	11.923 5	60.154 9	43.544 5	0.001 6	21.043 8	16.772 3
$F 3$	3.775 4E^-34	2.288 1E^-25	1.226 8E^-24	1.174 7E^-04	15.936 7	26.862 6	1.413 1E⁺⁰⁵	1.959 1E⁺⁰⁴	1.965 8E⁺⁰³
$F 4$	1.118 1E^-04	9.776 1E^-04	8.023 1E^-04	10.939 2	14.968 7	2.438 4	88.461 5	25.527 6	35.786 2
$F 5$	-1.031 1E⁺⁰⁴	-6.854 2E⁺⁰³	1.500 7	-4.132 1E⁺⁰³	-1.723 2E⁺⁰³	2.736 4	-8.988 1E⁺⁰³	-4.354 2E⁺⁰³	-3.346 1E⁺⁰³
$F 6$	1.414 2	2.533 7	0.551 3	4.596 4E⁺⁰²	1.590 1E⁺⁰³	6.278 3	2.374 2	1.936 2E⁺⁰³	3.263 4E⁺⁰²
$F 7$	1.038 1E^-12	6.059 2E^-05	1.753 3E^-04	7.918 4	2.100 5E⁺⁰⁴	4.980 3E⁺⁰⁴	0.216 7	49.246 1	2.165 8
$F 8$	8.713 4	8.890 2	0.071 2	2.422 3E⁺⁰⁴	2.163 5E⁺⁰⁵	1.402 1E⁺⁰⁵	28.841 1	4.514 2E⁺⁰⁵	1.221 4E⁺⁰⁵
$F 9$	0.013 9	0.226 4	0.139 3	7.454 6	16.077 6	5.403 9	0.694 7	16.439 9	3.563 9
$F 10$	8.665 6E^-29	4.628 5E^-23	2.242 2E^-22	51.025 4	4.324 9e⁺⁰²	3.508 1E⁺⁰²	0.000 4	2.262 9E⁺⁰³	5.226 2E⁺⁰²
$F 11$	2.019 5E^-05	7.139 4E^-04	0.000 7	0.007 1	0.016 3	0.007 2	0.078 3	0.787 8	0.112 3

表2

图5

图6

表3

图7

表4

图8

图9

表5

图10

图11

图12

图13

表6

参考文献 15

1	钱令希. 工程结构优化设计[M]. 北京: 科学出版社, 2011.
2	张涵. 基于元启发式算法的设施选址问题研究[D]. 哈尔滨: 哈尔滨工业大学计算机科学与技术学院, 2020.
	Zhang Han. Solving facility location problems based on meta- heuristic algorithms[D]. Harbin: College of Computer Science and Technology, Harbin Institute of Technology, 2020.
3	Jiang F, Wang L, Bai L. An improved whale algorithm and its application in truss optimization[J]. Journal of Bionic Engineering, 2021, 18: 721-732.
4	Wang G G, Gandomi A H, Alavi A H, et al. Hybrid krill herd algorithm with differential evolution for global numerical optimization[J]. Neural Computing and Applications, 2014, 25(2): 297-308.
5	Wang G, Guo L, Wang H, et al. Incorporating mutation scheme into krill herd algorithm for global numerical optimization[J]. Neural Computing and Applications, 2014, 24(3): 853-871.
6	Guo L, Wang G G, Gandomi A H, et al. A new improved krill herd algorithm for global numerical optimization[J]. Neurocomputing, 2014, 138: 392-402.
7	郭辉, 付接递, 李振东, 等. 基于改进鲸鱼算法优化SVM参数和特征选择[J]. 吉林大学学报: 工学版, 2023, 53(10): 2952-2963.
	Guo Hui, Fu Jie-di, Li Zhen-dong, et al. Optimization of SVM parameters and feature selection based on improved whale algorithm[J]. Journal of Jilin University (Engineering Science), 2023, 53(10): 2952-2963.
8	Tian D, Shi Z. MPSO: modified particle swarm optimization and its applications[J]. Swarm and Evolutionary Computation, 2018, 41: 49-68.
9	杨学惠, 李广强, 张新勋, 等. 基于 Matlab 的自适应算法仿真平台的设计与实现[J]. 信息化研究, 2010, 2010(6): 33-35.
	Yang Xue-hui, Li Guang-qiang, Zhang Xin-xun, et al. Design and development of adaptive algorithms simulation platform based on Matlab[J]. Informatization Research, 2010, 2010(6): 33-35.
10	朱冰, 赵健, 李静, 等. 面向牵引力控制系统的AMESim与MATLAB联合仿真平台[J]. 吉林大学学报: 工学版, 2008, 38(): 23-27.
	Zhu Bing, Zhao Jian, Li Jing, et al. AMESim and MATLAB co-simulation platform for traction control system[J]. Journal of Jilin University (Engineering and Technology Edition), 2008, 38(Sup.1): 23-27.
11	Senkerik R, Pluhacek M, Zelinka I, et al. Performance of chaos driven differential evolution on shifted benchmark functions set[C]// International Joint Conference SOCO´13-CISIS'13-ICEUTE'13.Berlin: Springer, 2014: 41-50.
12	Zeng R, Wang Y. A chaotic simulated annealing and particle swarm improved artificial immune algorithm for flexible job shop scheduling problem[J]. EURASIP Journal on Wireless Communications and Networking, 2018, 2018(1): 1-10.
13	Mirjalili S, Lewis A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67.
14	安伟光. 结构系统可靠性和基于可靠性的优化设计[M]. 北京: 国防工业出版社, 1997.
15	Renkavieski C, Parpinelli R S. Meta-heuristic algorithms to truss optimization: Literature mapping and application[J]. Expert Systems with Applications, 2021, 182: No.115197.

相关文章 15

[1]	阎奇武,邹忠亮. 减震结构阻尼器优化布置混合算法[J]. 吉林大学学报(工学版), 2024, 54(8): 2267-2274.
[2]	张广泰,周乘孝,刘诗拓. 盐渍土环境下纤维锂渣混凝土柱恢复力模型[J]. 吉林大学学报(工学版), 2024, 54(7): 1944-1957.
[3]	刁延松,任义建,杨元强,赵凌云,刘秀丽,刘芸. 带有摩擦耗能组件的可更换钢梁柱拼接节点抗震性能试验[J]. 吉林大学学报(工学版), 2024, 54(6): 1643-1656.
[4]	樊学平,刘月飞. 基于改进高斯混合粒子滤波新算法的桥梁极值应力动态预测[J]. 吉林大学学报(工学版), 2024, 54(4): 1038-1044.
[5]	刘一凡,缪志伟,申晨,耿祥东. 基于蒙特卡罗法的不均匀锈蚀钢筋力学性能评估[J]. 吉林大学学报(工学版), 2024, 54(4): 1007-1015.
[6]	樊学平,周衡,刘月飞. 基于Gaussian Copula-贝叶斯动态模型的桥梁构件时变可靠性分析[J]. 吉林大学学报(工学版), 2024, 54(2): 485-493.
[7]	刘玉梅,盛佳香,庄娇娇,陈熔,赵大龙. 高速变轨距转向架结构优化及动力学性能分析与预测[J]. 吉林大学学报(工学版), 2024, 54(2): 453-460.
[8]	范亮,徐英铭,谭阳. 集束群钉式装配组合梁界面滑移计算[J]. 吉林大学学报(工学版), 2023, 53(9): 2533-2541.
[9]	樊学平,周衡,刘月飞. 桥梁时变可靠性的多过程贝叶斯动态混合预测[J]. 吉林大学学报(工学版), 2023, 53(8): 2332-2338.
[10]	熊二刚,巩忠文,罗佳明,范团结. 基于数字图像相关技术的钢筋混凝土梁裂缝试验[J]. 吉林大学学报(工学版), 2023, 53(4): 1094-1104.
[11]	王晓东,李宁静,李强. 高压脉冲放电破碎混凝土梁试验[J]. 吉林大学学报(工学版), 2023, 53(2): 496-504.
[12]	匡亚川,陈立斌,李超举,贺宇豪. 栓钉剪力连接件力学性能分析[J]. 吉林大学学报(工学版), 2023, 53(2): 538-546.
[13]	白丽丽,姜封国,周玉明,曾枭. 基于改进鲸鱼算法的结构可靠性优化设计[J]. 吉林大学学报(工学版), 2023, 53(11): 3160-3165.
[14]	戴理朝,周亮,杨晓文,王磊. 基于Connector单元的锈蚀RC梁界面粘结性能细观数值模拟[J]. 吉林大学学报(工学版), 2023, 53(10): 2886-2896.
[15]	顿国强,刘文辉,毛宁,吴星澎,纪文义,马洪岩. 交替换岗式大豆小区育种排种器优化设计与试验[J]. 吉林大学学报(工学版), 2023, 53(1): 285-296.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

参数	数值
拉压屈服应力均值/MPa	275.8
屈服应力变异系数	0.15
材料弹性模量/MPa	2.06×10⁵
材料密度/（kg·m^-3）	2.7×10³
荷载的均值/kN	89
变异系数	0.15

元件编号	元件横截面面积/cm²
元件编号	SDEKH	KH	WOA	对偶规划法^［14］
1，7	19.073 2	19.123 5	19.105 9	19.06
2，8	13.548 9	13.555 6	13.620 4	13.56
3，9，12，13	11.361 2	11.361 4	11.360 4	11.37
4，10	11.503 8	11.506 3	11.511 8	11.66
5，11	3.401 2	3.455 6	3.384 7	3.638
6	8.768 6	8.863 2	8.857 2	8.729
结构总质量/kg	136.818 4	137.194 6	137.0481	137.6

结构设计变量	杆件编号	结构设计变量	杆件编号
1	1~4	9	37~40
2	5~12	10	41~48
3	13~16	11	49~52
4	17~18	12	53~54
5	19~22	13	55~58
6	23~30	14	59~66
7	31~34	15	67~70
8	35~36	16	71~72