温度和车辆荷载耦合产生的桥梁极值应力预测

doi:10.13229/j.cnki.jdxbgxb.20231358

吉林大学学报(工学版) ›› 2025, Vol. 55 ›› Issue (5): 1588-1594.doi: 10.13229/j.cnki.jdxbgxb.20231358

• 交通运输工程·土木工程 • 上一篇下一篇

温度和车辆荷载耦合产生的桥梁极值应力预测

樊学平^1,²(),杨渡²,李九谕²,赵启凡²,刘月飞^1,²

^1.兰州大学西部灾害与环境力学教育部重点实验室，兰州 730030
^2.兰州大学土木工程与力学学院，兰州 730030

收稿日期:2023-12-06 出版日期:2025-05-01 发布日期:2025-07-18
通讯作者: 樊学平 E-mail:fxp_2004@163.com
基金资助:
国家自然科学基金项目(51608243);兰州大学中央高校基本科研业务费专项项目(lzujbky-2025-05)

Dynamic prediction of bridge coupled extreme stresses produced by temperature and vehicle loads

Xue-ping FAN^1,²(),Du YANG²,Jiu-yu LI²,Qi-fan ZHAO²,Yue-fei LIU^1,²

^1.Key Laboratory of Mechanics on Disaster and Environment in Western China of the Ministry of Education，Lanzhou University，Lanzhou 730030，China
^2.School of Civil Engineering and Mechanics，Lanzhou University，Lanzhou 730030，China

Received:2023-12-06 Online:2025-05-01 Published:2025-07-18
Contact: Xue-ping FAN E-mail:fxp_2004@163.com

摘要/Abstract

摘要：

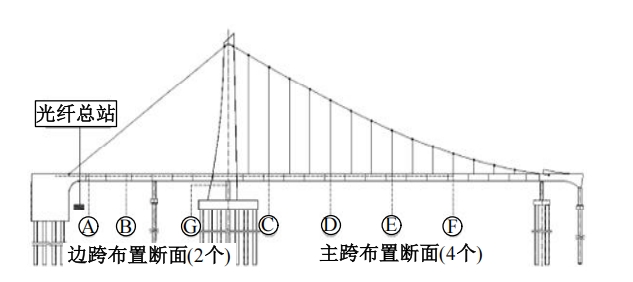
本文首先采用移动平均法对温度和车辆荷载耦合产生的监测极值应力进行平滑处理，取处理后的低频数据为趋势项信息，初始数据减去趋势项数据为车辆荷载效应信息，趋势项减去其均值为温度荷载效应信息，通过以上步骤来实现桥梁极值应力的解耦。其次，建立双变量贝叶斯动态线性趋势性模型（BDLTM）对低频极值应力进行预测分析，采用GRU神经网络模型对高频极值应力进行预测分析。最后，进行耦合极值应力的叠加预测，利用天津富民桥的监测耦合数据验证所建模型的可行性。本文研究成果将为桥梁的预防性养护维护决策提供理论基础。

关键词: 结构工程, 桥梁耦合极值应力, 移动平均法, BDLTM-GRU模型, BDLTM, GRU神经网络

Abstract:

Firstly， moving average method is adopted to decouple the coupled extreme stresses produced by temperature and vehicle loads， the low-frequency data after processed by moving average method is the trend item information， the initial data minus the trend item is the vehicle load effect information， and the trend item minus its mean is the temperature load effect information. Secondly， a bivariate Bayesian dynamic linear trend model （BDLTM） is built to predict and analyze low-frequency extreme stress， GRU neural network model is provided to predict and analyze high-frequency extreme stresses. Finally， the dynamic coupled extreme stresses are predicted. The monitoring coupled data from Tianjin Fumin Bridge is provided to illustrate the feasibility and application of the proposed model. The research results of this paper will provide the theoretical foundation for preventive maintenance and decision-making of the service bridges.

Key words: structural engineering, bridge coupled extreme stresses, moving average method, BDLTM-GRU, BDLTM, GRU neural network

中图分类号:

TU39

樊学平,杨渡,李九谕,赵启凡,刘月飞. 温度和车辆荷载耦合产生的桥梁极值应力预测[J]. 吉林大学学报(工学版), 2025, 55(5): 1588-1594.

Xue-ping FAN,Du YANG,Jiu-yu LI,Qi-fan ZHAO,Yue-fei LIU. Dynamic prediction of bridge coupled extreme stresses produced by temperature and vehicle loads[J]. Journal of Jilin University(Engineering and Technology Edition), 2025, 55(5): 1588-1594.

图/表 4

图1

图2

图3

表1

参考文献 13

[1]	樊学平, 吕大刚. 基于 BDNM 的桥梁结构可靠度预测 [J] .哈尔滨工业大学学报, 2014, 46(2): 1-5.
	Fan Xue-ping, Da-gang Lyu. Reliability prediction of bridge structures based on BDNM[J]. Journal of Harbin Institute of Technology, 2014, 46(2): 1-5.
[2]	李顺龙. 基于健康监测技术的桥梁结构状态评估和预警方法研究[D]. 哈尔滨:哈尔滨工业大学土木工程学院,2009.
	Li Shun-long. Approaches of condition assessment and damage alarming of bridges based on structural health monitoring[D]. Harbin:School of Civil Engineering, Harbin Institute of Technology,2009.
[3]	An Y H, Chatzi E, Sim S H, et al. Recent progress and future trends on damage identification methods for bridge structures[J]. Structural Control and Health Monitoring, 2019, 26(10): 2416.
[4]	Wan H P, Ren W X. Stochastic model updating utilizing Bayesian approach and Gaussian process model[J]. Mechanical Systems and Signal Processing, 2016, 70: 245-268.
[5]	Fan X P, Liu Y F. Use of monitored daily extreme stress data for performance prediction of steel bridges: dynamic linear models and gaussian mixed particle filter[J]. Mechanical Systems and Signal Processing, 2019, 121: 841-855.
[6]	樊学平, 吕大刚. 基于贝叶斯 DLM 的桥梁结构可靠度预测[J]. 铁道学报, 2014, 36(6): 93-98.
	Fan Xue-ping, Da-gang Lyu. Reliability prediction of aging bridges based on Bayesian dynamic linear model[J]. Journal of the China Railway Society, 2014, 36(6): 93-98.
[7]	樊学平, 刘月飞, 吕大刚. 桥梁监测数据的动态线性建模与可靠性预测[J]. 同济大学学报: 自然科学版, 2016, 44(7): 1002-1009.
	Fan Xue-ping, Liu Yue-fei, Da-gang Lyu. Dynamic linear modeling of bridge monitored data and reliability prediction[J]. Journal of Tongji University (Natural Science), 2016, 44(7): 1002-1009.
[8]	樊学平, 杨光红, 刘月飞. 大跨混凝土桥梁耦合极值应变的混合粒子预测[J]. 哈尔滨工程大学学报, 2021, 42(8): 1167-1175.
	Fan Xue-ping, Yang Guang-hong, Liu Yue-fei. Hybrid particle prediction of coupling extreme strain data of long-span concrete bridges[J]. Journal of Harbin Engineering University, 2021, 42(8): 1167-1175.
[9]	Petris G, Petrone S, Campagnoli P. Dynamic Linear Models with R[M]. Berlin: Springer Science & Business Media, 2009.
[10]	West M, Harrison J. Bayesian Forecasting and Dynamic Models[M]. Berlin: Springer Science & Business Media, 2006.
[11]	樊学平. 基于验证荷载和监测数据的桥梁可靠性修正与贝叶斯预测[D]. 哈尔滨: 哈尔滨工业大学土木工程学院, 2014.
	Fan Xue-ping. Reliability updating and Bayesian prediction of bridges based on proof loads and monitoring data[D]. Harbin:School of Civil Engineering, Harbin Institute of Technology,2014.
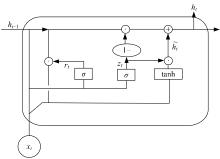
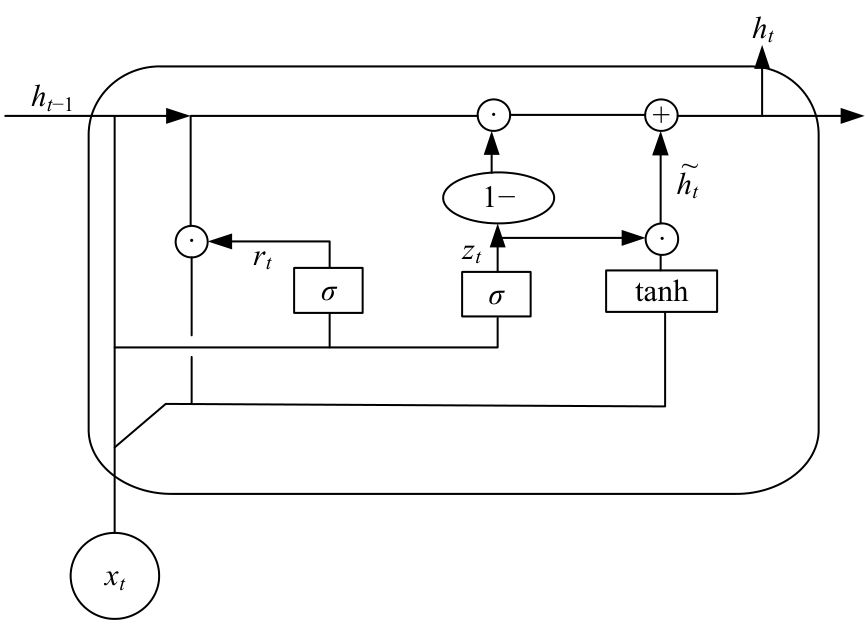
[12]	Cho K, Van M B, Bahdanau D, et al. On the properties of neural machine translation: encoder-decoder approaches[J]. Syntax, Semantics and Structure in Statistical Translation, 2014, 14: 103-111.
[13]	鞠翰文, 邓扬, 李爱群. 基于GRU神经网络的结构异常监测数据修复方法[J]. 振动与冲击, 2023, 42(9): 328-338.
	Ju Han-wen, Deng Yang, Li Ai-qun. Restoring method of structural abnormal monitoring data based on GRU neural network[J]. Journal of Vibration and Shock, 2023, 42(9): 328-338.

相关文章 15

[1]	梅生启,刘晓东,王兴举,李旭峰,武腾,程相旭. 基于参数相关性分析和机器学习算法的高强混凝土徐变预测[J]. 吉林大学学报(工学版), 2025, 55(5): 1595-1603.
[2]	张亮亮,程桦,王晓健. 常规三轴压缩下高强混凝土能量演化和破坏准则[J]. 吉林大学学报(工学版), 2025, 55(3): 974-985.
[3]	周宇,李萌,狄生奎,石贤增,陈东. 变截面两铰拱推力影响线解析解及损伤识别应用[J]. 吉林大学学报(工学版), 2025, 55(2): 664-672.
[4]	王羽岱,王斌,苗福生,马楠. 水热耦合变化下衬砌渠道冻胀响应[J]. 吉林大学学报(工学版), 2025, 55(1): 256-268.
[5]	姜浩,赵正文. 玄武岩纤维网格水泥基复合材料加固RC梁抗剪性能试验[J]. 吉林大学学报(工学版), 2025, 55(1): 211-220.
[6]	韦芳芳,李丽萍,徐庆鹏,赵有正,杨晶晶. 受火双钢板-混凝土组合剪力墙加固后抗震性能试验[J]. 吉林大学学报(工学版), 2025, 55(1): 230-244.
[7]	赵金全,周龙,丁永刚,朱熔基. 螺旋箍筋-波纹管浆锚连接锚固性能试验[J]. 吉林大学学报(工学版), 2024, 54(9): 2484-2494.
[8]	杨伟松,张安,许卫晓,李海生,杜轲. 刚度增强型金属连梁阻尼器的抗震性能[J]. 吉林大学学报(工学版), 2024, 54(9): 2469-2483.
[9]	阎奇武,邹忠亮. 减震结构阻尼器优化布置混合算法[J]. 吉林大学学报(工学版), 2024, 54(8): 2267-2274.
[10]	姜封国,周玉明,白丽丽,梁爽. 改进磷虾群算法及其在结构优化中的应用[J]. 吉林大学学报(工学版), 2024, 54(8): 2256-2266.
[11]	张广泰,周乘孝,刘诗拓. 盐渍土环境下纤维锂渣混凝土柱恢复力模型[J]. 吉林大学学报(工学版), 2024, 54(7): 1944-1957.
[12]	刁延松,任义建,杨元强,赵凌云,刘秀丽,刘芸. 带有摩擦耗能组件的可更换钢梁柱拼接节点抗震性能试验[J]. 吉林大学学报(工学版), 2024, 54(6): 1643-1656.
[13]	樊学平,刘月飞. 基于改进高斯混合粒子滤波新算法的桥梁极值应力动态预测[J]. 吉林大学学报(工学版), 2024, 54(4): 1038-1044.
[14]	刘一凡,缪志伟,申晨,耿祥东. 基于蒙特卡罗法的不均匀锈蚀钢筋力学性能评估[J]. 吉林大学学报(工学版), 2024, 54(4): 1007-1015.
[15]	樊学平,周衡,刘月飞. 基于Gaussian Copula-贝叶斯动态模型的桥梁构件时变可靠性分析[J]. 吉林大学学报(工学版), 2024, 54(2): 485-493.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

监测点	BDLTM-GRU	BDLTM	GRU
FBG01074	0.586 6	0.665 4	0.684 8
FBG01076	0.502 3	0.540 0	0.545 5
FBG01077	0.656 6	0.743 5	0.771 3
FBG01078	0.332 0	0.386 7	0.435 1

温度和车辆荷载耦合产生的桥梁极值应力预测

Dynamic prediction of bridge coupled extreme stresses produced by temperature and vehicle loads

RICH HTML

PDF (PC)

摘要/Abstract

引用本文

使用本文

图/表 4

参考文献 13

相关文章 15

Metrics

本文评价

推荐阅读 10