模糊c-harmonic均值算法在不平衡数据上改进

doi:10.13229/j.cnki.jdxbgxb20190963

摘要/Abstract

摘要：

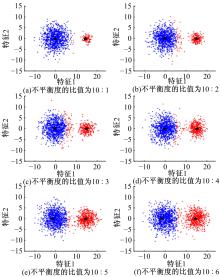
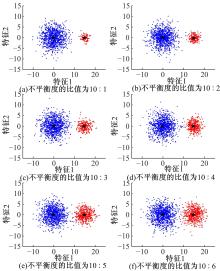
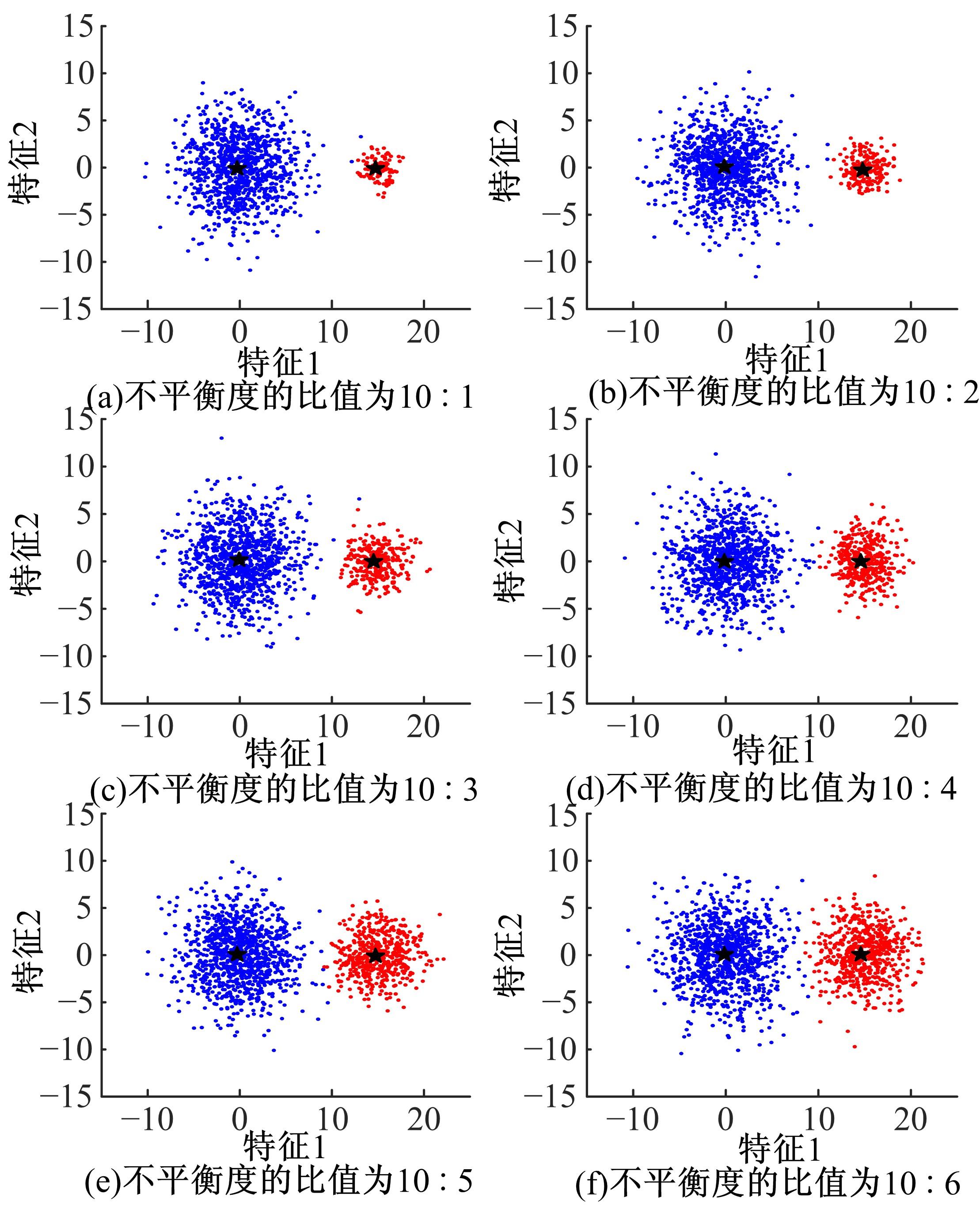
针对模糊c-harmonic均值算法（FCHM）在不平衡数据集上的聚类效果不理想的问题，提出了一种基于聚类体量约束的模糊c-harmonic均值算法。首先，利用隶属度矩阵定义各个类的体量，用于约束FCHM算法的代价函数，从而构建一个新的代价函数；然后，将该代价函数最小化，得到新的隶属度矩阵和聚类中心的计算公式；最后，在UCI数据集、模拟不平衡数据集及真实机床振动检测不平衡数据集上分别进行实验。实验结果表明，与同类算法相比，本文算法在保持传统算法全局最优性能的同时，在不平衡数据集上也能得到理想的聚类效果。

关键词: 人工智能, 聚类, 模糊c-harmonic均值算法, 全局最优, 不平衡数据

Abstract:

A new fuzzy c-harmonic means clustering algorithm, which is based on cluster volumes constraint, is proposed in this paper to solve the problem of imperfect clustering performance of traditional algorithm for imbalanced data set. Firstly, a quantity is defined by the membership matrix to measure the volume of each cluster, which is then used to construct a new objective function by combining with that of traditional algorithm. Secondly, new membership matrix and cluster center formulas are obtained by minimizing this new objective function. The proposed algorithm was tested on the UCI data sets, simulated imbalanced data sets and actual machine vibration detection imbalanced data sets. Experimental results show that, compared with several peer algorithms, the proposed algorithm achieved good clustering performance for imbalanced data sets while maintaining the global optimal performance of the traditional one.

Key words: artificial intelligence, clustering, fuzzy c-harmonic mean algorithm, global optimality, unbalanced data

中图分类号:

TP391

刘富,梁艺馨,侯涛,宋阳,康冰,刘云. 模糊c-harmonic均值算法在不平衡数据上改进[J]. 吉林大学学报(工学版), 2021, 51(4): 1447-1453.

Fu LIU,Yi-xin LIANG,Tao HOU,Yang SONG,Bing KANG,Yun LIU. Improvement of fuzzy c-harmonic mean algorithm on unbalanced data[J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(4): 1447-1453.

图/表 8

图1

表1

表2

表3

图2

图3

图4

表4

参考文献 23

1	Henao-Restrepo A M, Camacho A, Longini I M, et al. Efficacy and effectiveness of an rVSV-vectored vaccine in preventing Ebola virus disease: final results from the guinea ring vaccination open-label cluster-randomised trial[J]. Lancet, 2017, 389(10068): 505-518.
2	Huzurbazar S, Kuang D Y, Lee L. Landmark-based algorithms for group average and pattern recognition[J]. Pattern Recognition, 2019, 86: 172-187.
3	刘云, 刘富, 侯涛,等. 优化核参数的模糊C均值聚类算法[J]. 吉林大学学报:工学版, 2016, 46(1):246-251.
	Liu Yun, Liu Fu, Hou Tao, et al. Kernel-based fuzzy C-means clustering method based on parameter optimization[J]. Journal of Jilin University(Engineering and Technology Edition), 2016, 46(1): 246-251.
4	Gao Z M, Wang L, Zhou L P. A probabilistic approach to cross-region matching-based image retrival[J]. IEEE Transactions on Image Processing, 2019, 28(3): 1191-1204.
5	Zhang B. Generalized k-harmonic Means-Boosting in unsupervised Learning[M]. Palo Alto: Hewlett, 2000.
6	Zhang B, Hsu M, Dayal U. K-harmonic means-a spatial clustering algorithm with boosting[C]∥International Workshop on Temporal, Spatial, and Spatio-Temporal Data Mining, Lyon, France, 2000, 12: 31-45.
7	Wu X H, Wu B, Sun J, et al. A hybrid fuzzy K-harmonic means clustering algorithm[J]. Applied Mathematical Modelling, 2015, 39(12): 3398-3409.
8	Jiang H, Yi S, Li J, et al. Ant clustering algorithm with K -harmonic means clustering[J]. Expert Systems with Applications, 2010, 37(12): 8679-8684.
9	汪中, 刘贵全, 陈恩红. 基于模糊K-harmonic means的谱聚类算法[J]. 智能系统学报, 2009,4(2): 95-99.
	Wang Zhong, Liu Gui-quan, Chen En-hong, et al. A spectral clustering algorithm based on fuzzy K-harmonic means[J]. CAAI Tranctions on Intelligent Systems, 2009, 4(2): 95-99.
10	Yang F, Sun T, Zhang C. An efficient hybrid data clustering method based on K-harmonic means and particle swarm optimization[J]. Expert Systems with Applications, 2009, 36(6): 9847-9852.
11	赵恒, 杨万海, 张高煜. 模糊K-Harmonic Means聚类算法[J]. 西安电子科技大学学报:自然科学版, 2005,32(4):603-606, 638.
	Zhao Heng, Yang Wan-hai, Zhang Gao-yu, et al. Fuzzy K-Harmonic Means clustering algorithm[J]. Journal of Xidian University(Natural Science), 2005, 32(4): 603-606, 638.
12	Bensaid A M, Hall L O, Bezdek J C. Partially supervised clustering for image segmentation[J]. Pattern Recognition, 1996, 29(5): 859-871.
13	Noordam J C, van den Broek W H A M, Buydens L M C. Multivariate image segmentation with cluster size insensitive fuzzy C-means[J]. Chemometrics and Intelligent Laboratory Systems, 2002, 64(1): 65-78.
14	Liang J Y, Bai L, Dang C Y, et al. The K-Means-Type algorithms versus imbalanced data distributions[J]. IEEE Transactions on Fuzzy Systems, 2012, 20(4): 728-745.
15	Likas A, Vlassis N, Verbeek J J. The global k-means clustering algorithm[J]. Pattern Recognition, 2002, 36(2): 451-461.
16	Bagirov A M. Modified global k-means algorithm for minimum sum-of-squares clustering problems[J]. Pattern Recognition, 2008, 41(10): 3192-3199.
17	Zhang Bin, Hsu M, Dayal U, et al. K-Harmonic means—a data clustering algorithm[J]. Hewlett Packard Research Laboratory Technical Report, 1999.
18	Kim D W, Lee K H, Lee D. On cluster validity index for estimation of the optimal number of fuzzy clusters[J]. Pattern Recognition, 2004, 37(10): 2009-2025.
19	Capitaine H L, Frelicot C. A cluster-validity index combining an overlap measure and a separation measure based on fuzzy-aggregation operators[J]. IEEE Transactions on Fuzzy Systems, 2011, 19(3): 580–588.
20	Zahid N, Limouri M, Essaid A. A new cluster-validity for fuzzy clustering[J]. Pattern Recognition, 1999, 32(7): 1089-1097.
21	Wu K L, Yang M S. A cluster validity index for fuzzy clustering[J]. Pattern Recognition Letters, 2005, 26(9): 1275-1291.
22	Han H, Wang W Y, Mao B H. Borderline-SMOTE: a new over-sampling method in imbalanced data sets learning[J]. International Conference on Intelligent Computing, 2005, 3644(5): 878-887.
23	Su C T, Chen L S, Yih Y. Knowledge acquisition through information granulation for imbalanced data[J]. Expert Systems with Applications, 2006, 31(3): 531-541.

相关文章 15

[1]	赵亚慧,杨飞扬,张振国,崔荣一. 基于强化学习和注意力机制的朝鲜语文本结构发现[J]. 吉林大学学报(工学版), 2021, 51(4): 1387-1395.
[2]	董延华,刘靓葳,赵靖华,李亮,解方喜. 基于BPNN在线学习预测模型的扭矩实时跟踪控制[J]. 吉林大学学报(工学版), 2021, 51(4): 1405-1413.
[3]	朱才华,孙晓黎,李岩. 站点分类下的城市公共自行车交通需求预测[J]. 吉林大学学报(工学版), 2021, 51(2): 531-540.
[4]	尚福华,曹茂俊,王才志. 基于人工智能技术的局部离群数据挖掘方法[J]. 吉林大学学报(工学版), 2021, 51(2): 692-696.
[5]	赵海英,周伟,侯小刚,张小利. 基于多任务学习的传统服饰图像双层标注[J]. 吉林大学学报(工学版), 2021, 51(1): 293-302.
[6]	欧阳丹彤,马骢,雷景佩,冯莎莎. 知识图谱嵌入中的自适应筛选[J]. 吉林大学学报(工学版), 2020, 50(2): 685-691.
[7]	李贻斌,郭佳旻,张勤. 人体步态识别方法与技术[J]. 吉林大学学报(工学版), 2020, 50(1): 1-18.
[8]	宗长富,文龙,何磊. 基于欧几里得聚类算法的三维激光雷达障碍物检测技术[J]. 吉林大学学报(工学版), 2020, 50(1): 107-113.
[9]	刘巧斌,史文库,陈志勇,骆联盟,苏志勇,黄开军. 混合可靠性模型参数的核密度和引力搜索估计[J]. 吉林大学学报(工学版), 2019, 49(6): 1818-1825.
[10]	李军军,曹建农,程贝贝,廖娟,朱莹莹. 联合像素与多尺度对象的高分辨率遥感影像谱聚类分割[J]. 吉林大学学报(工学版), 2019, 49(6): 2098-2108.
[11]	李宾,周旭,梅芳,潘帅宁. 基于K-means和矩阵分解的位置推荐算法[J]. 吉林大学学报(工学版), 2019, 49(5): 1653-1660.
[12]	徐谦,李颖,王刚. 基于深度学习的行人和车辆检测[J]. 吉林大学学报(工学版), 2019, 49(5): 1661-1667.
[13]	刘玉梅,乔宁国,庄娇娇,刘鹏程,胡婷,陈立军. 基于多传感器数据融合的轨道车辆齿轮箱异常检测[J]. 吉林大学学报(工学版), 2019, 49(5): 1465-1470.
[14]	高万夫,张平,胡亮. 基于已选特征动态变化的非线性特征选择方法[J]. 吉林大学学报(工学版), 2019, 49(4): 1293-1300.
[15]	欧阳丹彤,肖君,叶育鑫. 基于实体对弱约束的远监督关系抽取[J]. 吉林大学学报(工学版), 2019, 49(3): 912-919.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

数据集	样本数量	特征数量	类的个数	样本组成
Iris	150	4	2或3	50，50
Iris	150	4	2或3	50，50，50
Ionosphere	351	34	2	126，225
Pima Indians Diabetes	768	8	2	538，230
Breast Cancer1	683	10	2	458，225
Glass	214	9	2	163，51
Breast Cancer2	569	30	2	212，357
振动数据集	215	48 312	2	159，56

数据集	c	J_opt	本文算法
数据集	c	J_opt	J	E	N	t
Iris	2	152.35	152.37	0.01	16	0.03
			152.37	0.01	14	0.01
			152.37	0.01	18	0.01
			152.37	0.01	14	0.01
			152.37	0.01	15	0.01
	3	78.85	79.12	0.33	39	0.05
			79.12	0.33	30	0.02
			79.12	0.33	25	0.02
			79.12	0.33	37	0.03
			79.12	0.33	30	0.02
Ionosphere	2	2419.4	2420.01	0.03	33	0.09
			2420.01	0.03	44	0.12
			2420.01	0.03	36	0.11
			2420.01	0.03	30	0.06
			2420.01	0.03	53	0.14
Pima Indians Diabetes	2	5.14e6	5.18e6	0.68	43	0.19
			5.18e6	0.68	34	0.12
			5.18e6	0.68	43	0.15
			5.18e6	0.68	36	0.14
			5.18e6	0.68	35	0.13
Breast Cancer1	2	1.93e5	1.93e5	0.00	13	0.05
			1.93e5	0.00	15	0.06
			1.93e5	0.00	18	0.06
			1.93e5	0.00	19	0.06
			1.93e5	0.00	16	0.05

数据集	c	J_opt	GKM			MGKM			本文算法
数据集	c	J_opt	E	N	t	E	N	t	E	N	t
Iris	2	152.35	0.00	1.26e4	0.00	0.00	3.55e4	0.00	0.01	13	0.01
Iris	3	78.85	0.01	1.78e4	0.00	0.00	6.34e4	0.00	0.33	22	0.02
Ionosphere	2	2.42e3	0.00	6.63e4	0.03	0.00	1.90e5	0.05	0.03	16	0.03
Pima Indians Diabetes	2	5.14e6	0.00	3.18e5	0.06	0.00	9.09e5	0.09	0.68	35	0.12
Breast Cancer1	2	1.93e5	0.00	2.42e5	0.05	0.00	7.09e5	0.06	0.00	12	0.04

模拟数据集	FCHM		siibFCM		本文算法
模拟数据集	F- value	G-mean	F- value	G-mean	F- value	G-mean
a	0.8621	0.9839	0.9615	0.9960	0.9950	0.9950
b	0.9639	0.9925	0.6700	0.8961	0.9975	0.9975
c	0.9709	0.9910	0.8772	0.9571	0.9967	0.9967
d	0.9913	0.9965	0.9467	0.9772	0.9937	0.9967
e	0.9930	0.9965	0.9718	0.9854	0.9940	0.9970
f	0.9893	0.9932	0.9748	0.9844	0.9933	0.9943
Glass	0.7961	0.8658	0.7805	0.8659	0.8667	0.8745
Breast Cancer2	0.7112	0.7429	0.8779	0.9030	0.9055	0.9161
Ionosphere	0.6383	0.7099	0.6286	0.7025	0.7749	0.8278