Journal of Jilin University(Engineering and Technology Edition) ›› 2021, Vol. 51 ›› Issue (2): 728-737.doi: 10.13229/j.cnki.jdxbgxb20191174

Previous Articles    

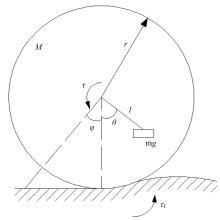
Adaptive fractional PIλDμ sliding mode control method for speed control of spherical robot

Ting ZHOU(),Yu-gong XU,Bin WU()   

  1. School of Mechanical，Electronic and Control Engineering，Beijing Jiaotong University，Beijing 100044，China
  • Received:2019-12-23 Online:2021-03-01 Published:2021-02-09
  • Contact: Bin WU E-mail:14116373@bjtu.edu.cn;bwu@bjtu.edu.cn

RICH HTML

 9   

PDF (PC)

371

Abstract:

The traditional hierarchical sliding mode control method applied directly to the spherical robot speed control will cause a long adjustment time and a large overshoot， which is hard to meet the requirements in practical application. In this paper， a new sliding surface with fractional order PIλDμstructure is proposed by introducing a derivative element and fractional order calculus. The asymptotic stability condition of the sliding surface is given. Based on the new fractional PIλDμ sliding surface， a velocity controller for the linear motion of the spherical robot is designed. Furthermore， an adaptive law is used to estimate the unknown rolling friction. The simulation results show that the new adaptive fractional sliding mode controller designed in this paper presents a better control performance and stronger robustness compared to the conventional one. Besides， the new controller can accurately estimate the unknown rolling friction.

Key words: control theory, fractional sliding mode, spherical robot, speed control, adaptive control

CLC Number: 

  • TP242.3

Fig.1

Diagram of spherical robot dynamical model in linear motion"

Table 1

Parameters of four controllers"

控制器参数取值
FO-PID ASMCλ11=2,λ2=12,λ12=0.5,η=2,ζ=2,k=6,w=5,α=0.1,β=0.1,ε=0.5
IO-PI ASMCλ11=0.7,λ12=12,η=2,ζ=2,k=6,w=5,ε=0.5
FO-PI ASMCλ11=2,λ12=12,η=2,ζ=2,k=6,w=5,α=0.1,ε=0.5
FO-PD ASMCλ11=2,λ12=12,η=2,ζ=2,k=6,w=5,α=0.1,ε=0.5

Fig.2

Velocity of shell response curves comparison among different controllers"

Table 2

Performance of three controllers without uncertain parameters"

控制器超调量 /%调节 时间/s稳态 误差/%恢复稳态 时间/s
FO-PID ASMC18.31.201.6
IO-PI ASMC40.53.901.8
FO-PI ASMC37.23.201.1

Fig.3

Curves of each second layer sliding mode surfaces S"

Fig.4

Curves of estimation of rolling friction"

Fig.5

Velocity of shell response curves comparison among different controllers with uncertain parameters"

Fig.6

Velocity of shell response curves when parameter λ11 changes"

Fig.7

Velocity of shell response curves when parameter λ12 changes"

Fig.8

Velocity of shell response curves when parameter α changes"

Fig.9

Velocity of shell response curves when parameter β changes"

1 Zhan Q, Cai Y, Yan C X. Design, analysis and experiments of an omni-directional spherical robot[C]∥2011 IEEE International Conference on Robotics and Automation, Piscataway, United States, 2011: 9-13.
2 Mattias S, Mathias B, Alessandro S, et al. An autonomous spherical robot for security tasks[C]∥Proceedings of the 2006 IEEE International Conference on Computational Intelligence for Homeland Security and Personal Safety, Piscataway, United States, 2006: 51-55.
3 Wang H Q, Liu P X, Xie X J, et al. Adaptive fuzzy asymptotical tracking control of nonlinear systems with unmodeled dynamics and quantized actuator[J/OL].[2018-04-03].
4 Liu D L, Sun H X, Jia Q X. A family of spherical mobile robot: driving ahead motion control by feedback linearization [C]∥2008 2nd International Symposium on Systems and Control in Aerospace and Astronautics, Piscataway, United States, 2008: 1-6.
5 Lin C M, Mon Y J. Decoupling control by hierarchical fuzzy sliding-mode controller[J]. IEEE Transactions on Control Systems Technology, 2005, 13(4):593-598.
6 Wu Y M, Sun N, Chen H, et al. Nonlinear time-optimal trajectory planning for varying-rope-length overhead cranes[J]. Assembly Automation, 2018, 38(5): 587-594.
7 Yang C G, Li Z J, Cui R X, et al. Neural network-based motion control of an underactuated wheeled inverted pendulum model[J]. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(11): 2004-2016.
8 Cai Y, Zhan Q, Xi X. Neural network control for the linear motion of a spherical mobile robot[J]. International Journal of Advanced Robotic Systems, 2011, 8(4): 79-87.
9 Utkin V. Variable structure systems with sliding modes[J]. IEEE Transactions on Automatic Control, 1977, 22(2): 212-222.
10 Xu R, Ümit Ö. Sliding mode control of a class of underactuated systems[J]. Automatica, 2008, 44(1): 233-241.
11 Lo J C, Kuo Y H. Decoupled fuzzy sliding-mode control[J]. IEEE Transactions on Fuzzy Systems, 2002, 6(3): 426-435.
12 韩京元, 田彦涛, 孔英秀, 等. 板球系统自适应解耦滑模控制[J]. 吉林大学学报: 工学版, 2014, 44(3): 718-725.
Han Jing-yuan, Tian Yan-tao, Kong Ying-xiu, et al. Adaptive decoupled sliding mode control for the ball and plate system[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(3):718-725.
13 Wang W, Yi J Q, Zhao D B, et al. Design of a stable sliding-mode controller for a class of second-order underactuated systems[J]. IEE Proceedings: Control Theory and Applications, 2004, 151(6): 683-690.
14 Barambones O, Aitor J G, Francisco J M. Integral sliding-mode controller for induction motor based on field-oriented control theory [J]. IET Control Theory and Applications, 2007, 1(3): 786-794.
15 Yue M, Liu B Y. Adaptive control of an underactuated spherical robot with a dynamic stable equilibrium point using hierarchical sliding mode approach[J]. International Journal of Adaptive Control and Signal Processing, 2014, 28(6): 523-535.
16 Yue M, Liu B Y, An C, et al. Extended state observer-based adaptive hierarchical sliding mode control for longitudinal movement of a spherical robot[J]. Nonlinear Dynamics, 2014, 78(2): 1233-1244.
17 Eker I. Sliding mode control with PID sliding surface and experimental application to an electromechanical plant[J]. Isa Transactions, 2006, 45(1): 109-118.
18 Igor P. Fractional-order systems and PID controllers[J]. IEEE Transactions on Automatic Control, 1999, 44(1): 208-214.
19 Ebrahimkhani S. Robust fractional order sliding mode control of doubly-fed induction generator (DFIG)-based wind turbines[J]. Isa Transactions, 2016, 63: 343-354.
20 Zhang B T, Pi Y G, Luo Y. Fractional order sliding-mode control based on parameters auto-tuning for velocity control of permanent magnet synchronous motor [J]. ISA Transactions, 2012, 51(5): 649-656.
21 黄家才, 施昕昕, 李宏胜, 等. 永磁同步电机调速系统的分数阶积分滑模控制[J]. 吉林大学学报: 工学版, 2014, 44(6): 1736-1742.
Huang Jia-cai, Shi Xin-xin, Li Hong-sheng, et al. Speed control of PMSM using fractural order integral sliding mode controller[J]. Journal of Jilin University(Engineering and Technology Edition), 2014, 44(6): 1736-1742.
22 Yue M, Deng Z Q, Yu X Y, et al. Introducing hit spherical robot: dynamic modeling and analysis based on decoupled subsystem[C]∥2006 IEEE International Conference on Robotics and Biomimetics, Piscataway, United States, 2006: 181-186.
23 Igor P. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications[M]. Amsterdam, The Netherlands: Elsevier, 1998.
24 Qian D L, Li C P, Agarwal R P, et al. Stability analysis of fractional differential system with riemann-liouville derivative[J]. Mathematical and Computer Modelling and International Journal, 2010, 52(5): 862-874.
25 Kibas A A, Srivastava H M, Trujillo J J. Theory and Applications of Fractional Differential Equations[M]. Amsterdam, The Netherlands: Elsevier Science Limited, 2006.
26 Deng W H, Li C P, Lu J H. Stability analysis of linear fractional differential system with multiple time delays[J]. Nonlinear Dynamics, 2007, 48(4): 409-416.
27 Tao G. A simple alternative to the Barbalat lemma[J]. IEEE Transactions on Automatic Control, 1997,42(5): 698.
28 Boiko I M. Analysis of chattering in sliding mode control systems with continuous boundary layer approximation of discontinuous control[C]∥Proceedings of the 2011 American Control Conference, Piscataway, United States, 2011: 757-762.
[1] Yan MA,Jian-fei HUANG,Hai-yan ZHAO. Method of vehicle formation control based on vehicle to vehicle communication [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(2): 711-718.
[2] Wei WANG,Jian-ting ZHAO,Kuan-rong HU,Yong-cang GUO. Trajectory tracking of robotic manipulators based on fast nonsingular terminal sliding mode [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(2): 464-471.
[3] GU Wan-li,WANG Ping,HU Yun-feng,CAI Shuo,CHEN Hong. Nonlinear controller design of wheeled mobile robot with H∞ performance [J]. Journal of Jilin University(Engineering and Technology Edition), 2018, 48(6): 1811-1819.
[4] LI Zhi-hui, XIA Ying-ji, QU Zhao-wei, REN Jing-chen. Data-driven background model in video surveillance [J]. 吉林大学学报(工学版), 2017, 47(4): 1286-1294.
[5] WANG Chun-yang, XIN Rui-hao, SHI Hong-wei. Decreasing time delay auto-disturbance rejection control method for large time delay systems [J]. 吉林大学学报(工学版), 2017, 47(4): 1231-1237.
[6] SHAO Ke-yong, CHEN Feng, WANG Ting-ting, WANG Ji-chi, ZHOU Li-peng. Full state based adaptive control of fractional order chaotic system without equilibrium point [J]. 吉林大学学报(工学版), 2017, 47(4): 1225-1230.
[7] DENG Li-fei, SHI Yao-wu, ZHU Lan-xiang, YU Ding-li. Failure detection of closed-loop systems and application to SI engines [J]. 吉林大学学报(工学版), 2017, 47(2): 577-582.
[8] LI Bing-qiang, CHEN Xiao-lei, LIN Hui, LYU Shuai-shuai, MA Dong-qi. High precision adaptive backstepping sliding mode control for electromechanical servo system [J]. 吉林大学学报(工学版), 2016, 46(6): 2003-2009.
[9] CAO Fu-cheng, XING Xiao-xue, LI Yuan-chun, ZHAO Xi-lu. Adaptive trajectory sliding mode impedance control for lower limb rehabilitation robot [J]. 吉林大学学报(工学版), 2016, 46(5): 1602-1608.
[10] HUANG Jing-ying, QIN Da-tong, LIU Yong-gang. Adaptive filter based antilock braking control of electro-hydraulic system for electric vehicle [J]. 吉林大学学报(工学版), 2016, 46(4): 1044-1051.
[11] QIAN Li-jun, HU Wei-long, LIU Qing, WU Bing. Multiple segment method for automatic parking path planning and its key technology [J]. 吉林大学学报(工学版), 2016, 46(3): 785-791.
[12] WANG Chun-yang, CAI Nian-chun, LI Ming-qiu, LIU Xue-lian. Robust fractional order proportional differential controller parameters algorithm based on phasor [J]. 吉林大学学报(工学版), 2015, 45(6): 1933-1940.
[13] WANG Jun-nian, ZHANG Xu, KANG Dan, WANG Qing-nian, TANG De-long, ZHANG Jun-yan. Parameter matching and cruising control of a solar race car with in-wheel motor [J]. 吉林大学学报(工学版), 2015, 45(3): 689-695.
[14] HUANG Jia-cai, SHI Xin-xin, LI Hong-sheng, XU Qing-hong, SHI Yao-wu. Speed control of PMSM using fractural order integral sliding mode controller [J]. 吉林大学学报(工学版), 2014, 44(6): 1736-1742.
[15] WU Ai-guo, YANG Shuo, ZHANG Han, LI Chang-bin. Leveling and tracking control of multi-cylinder forging hydraulic press [J]. 吉林大学学报(工学版), 2014, 44(4): 1051-1056.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
Copyright © Journal of Jilin University(Engineering and Technology Edition), All Rights Reserved.
Tel: +86-431-85095297　Fax: +86-431-85094074　E-mail: xbgxb@jlu.edu.cn
Powered by Beijing Magtech Co. Ltd