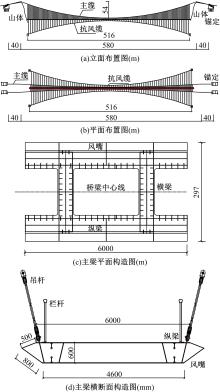
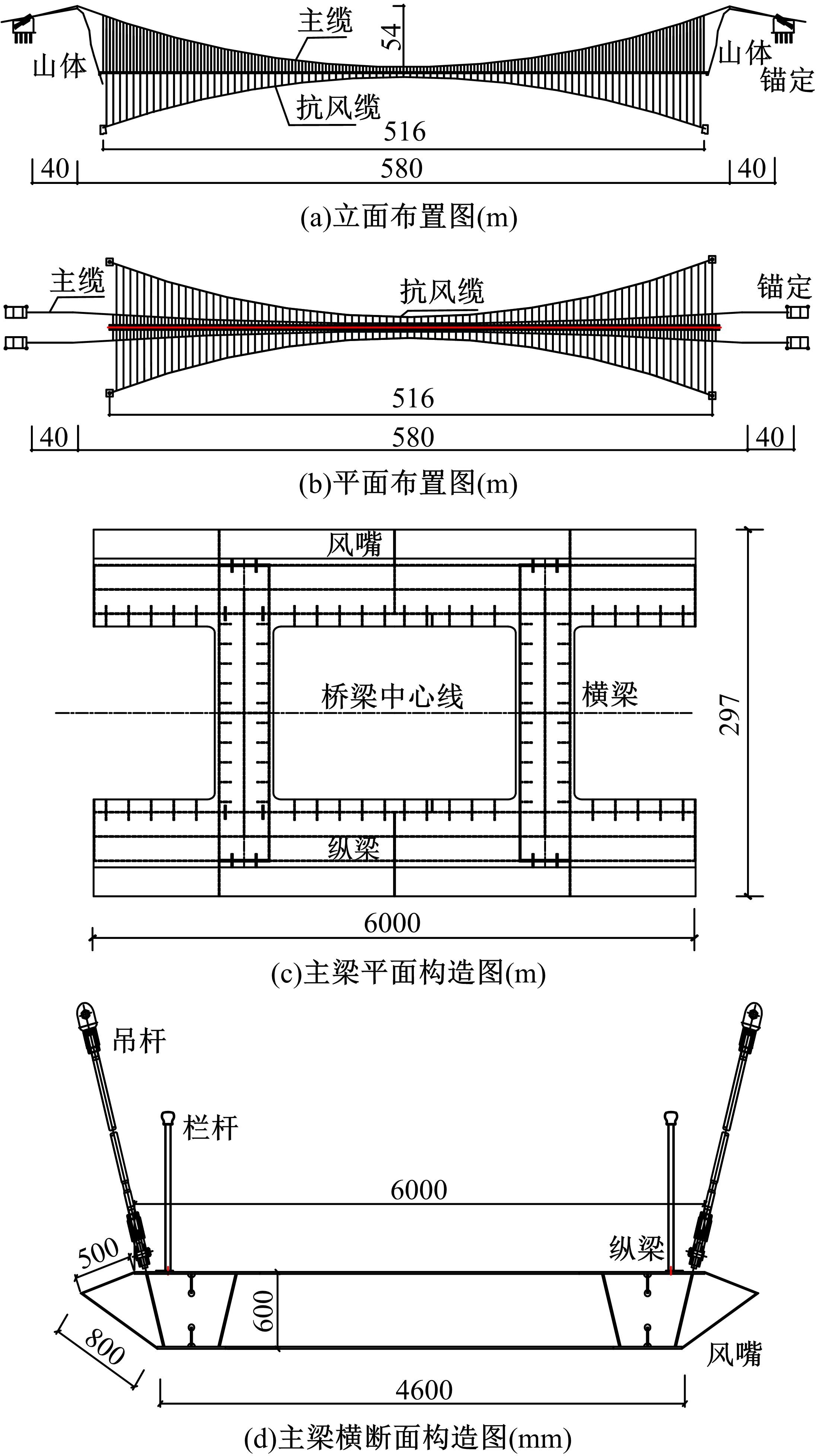
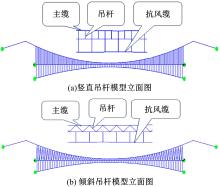
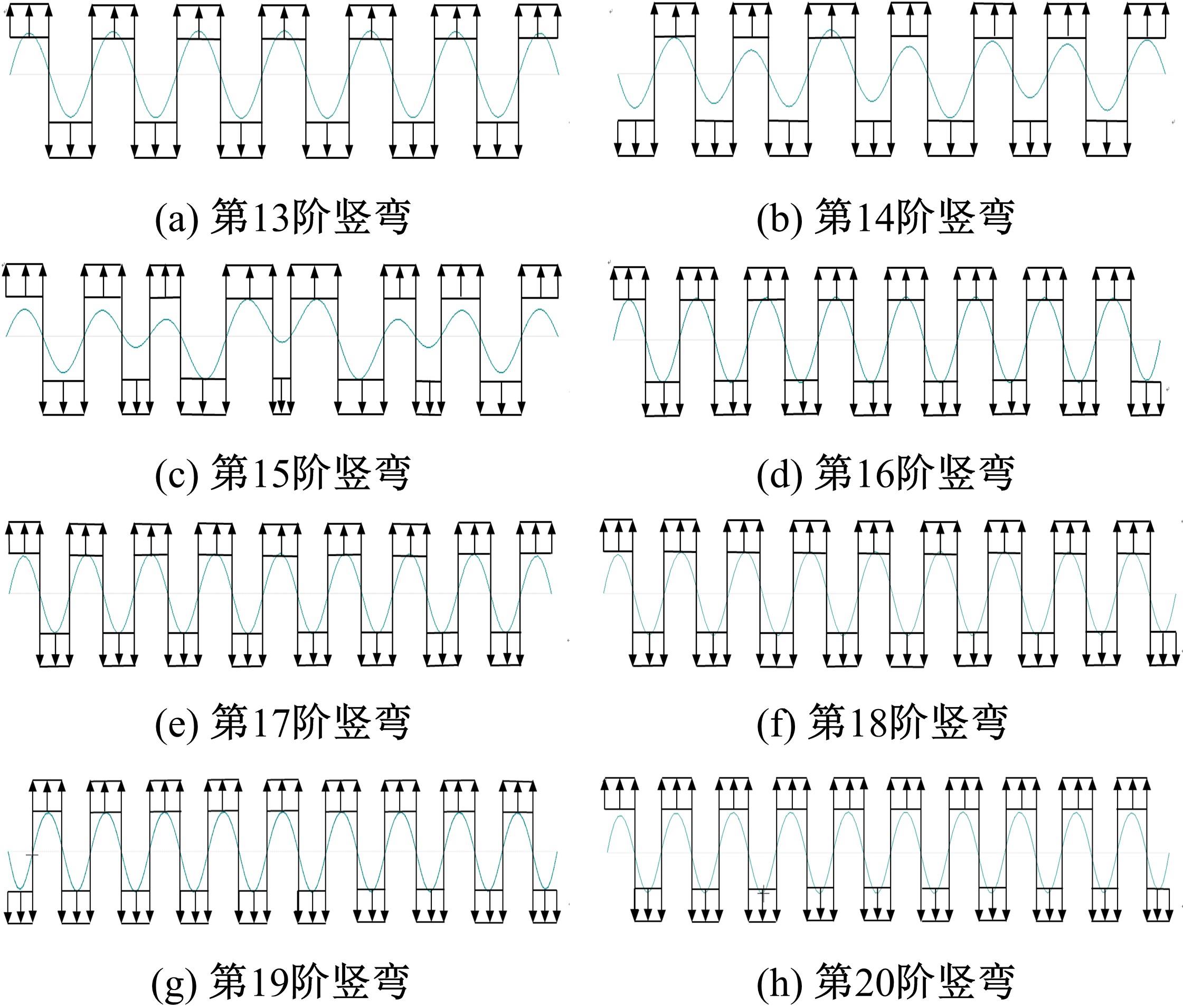
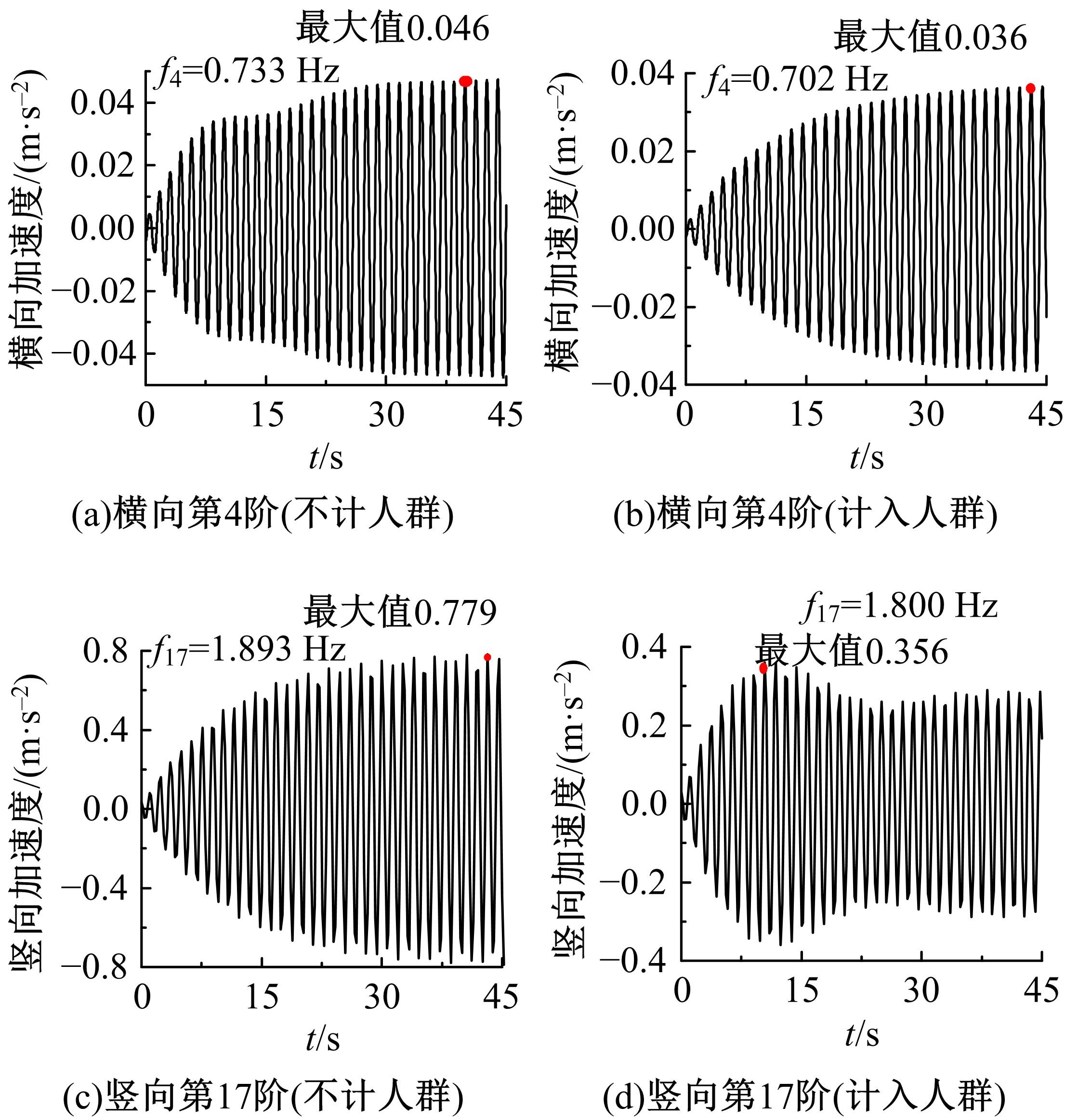
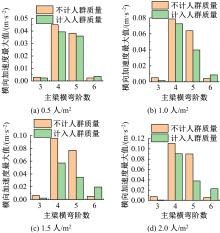
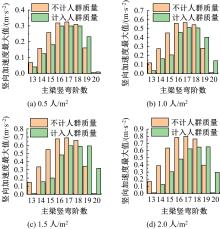
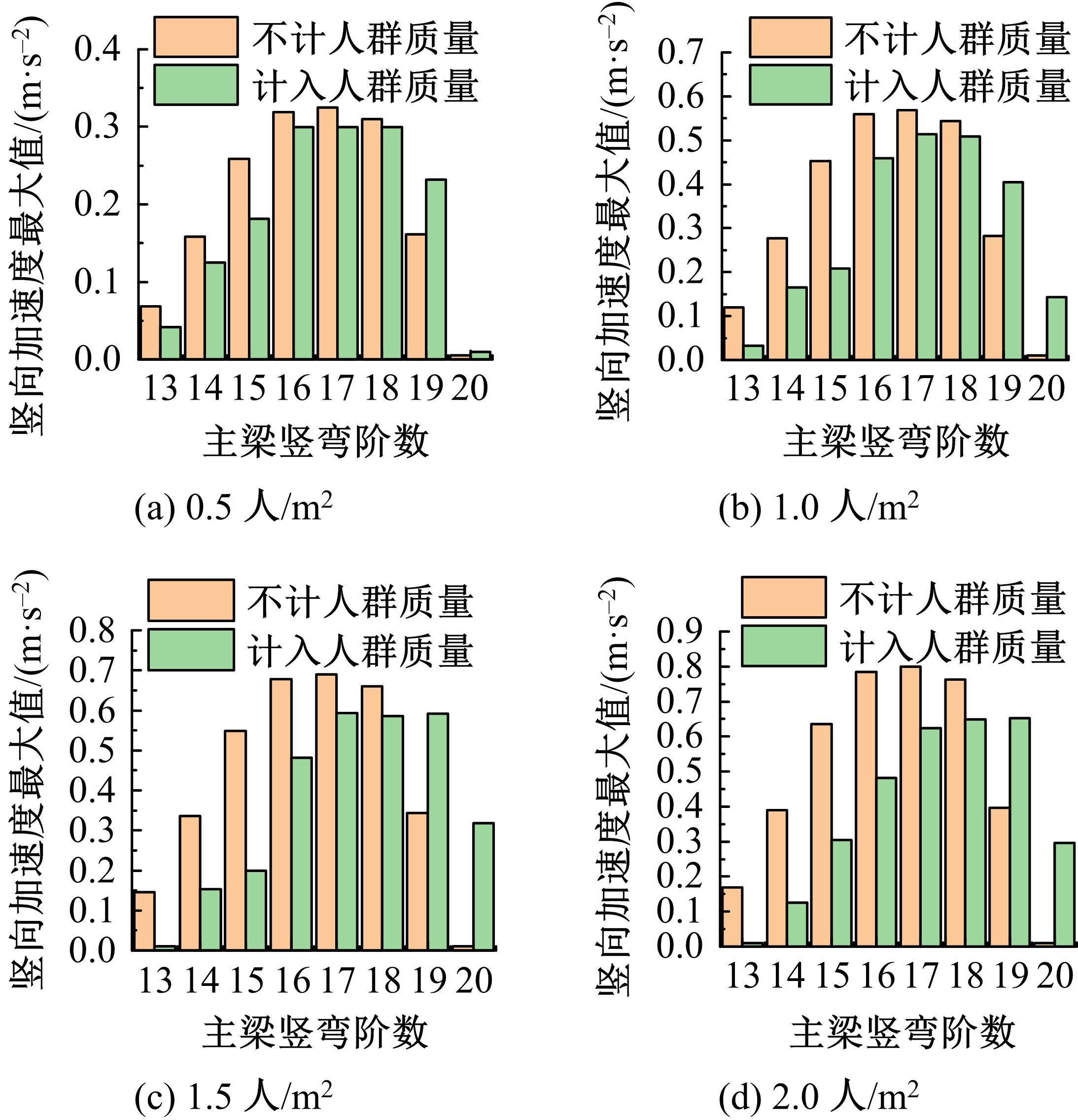
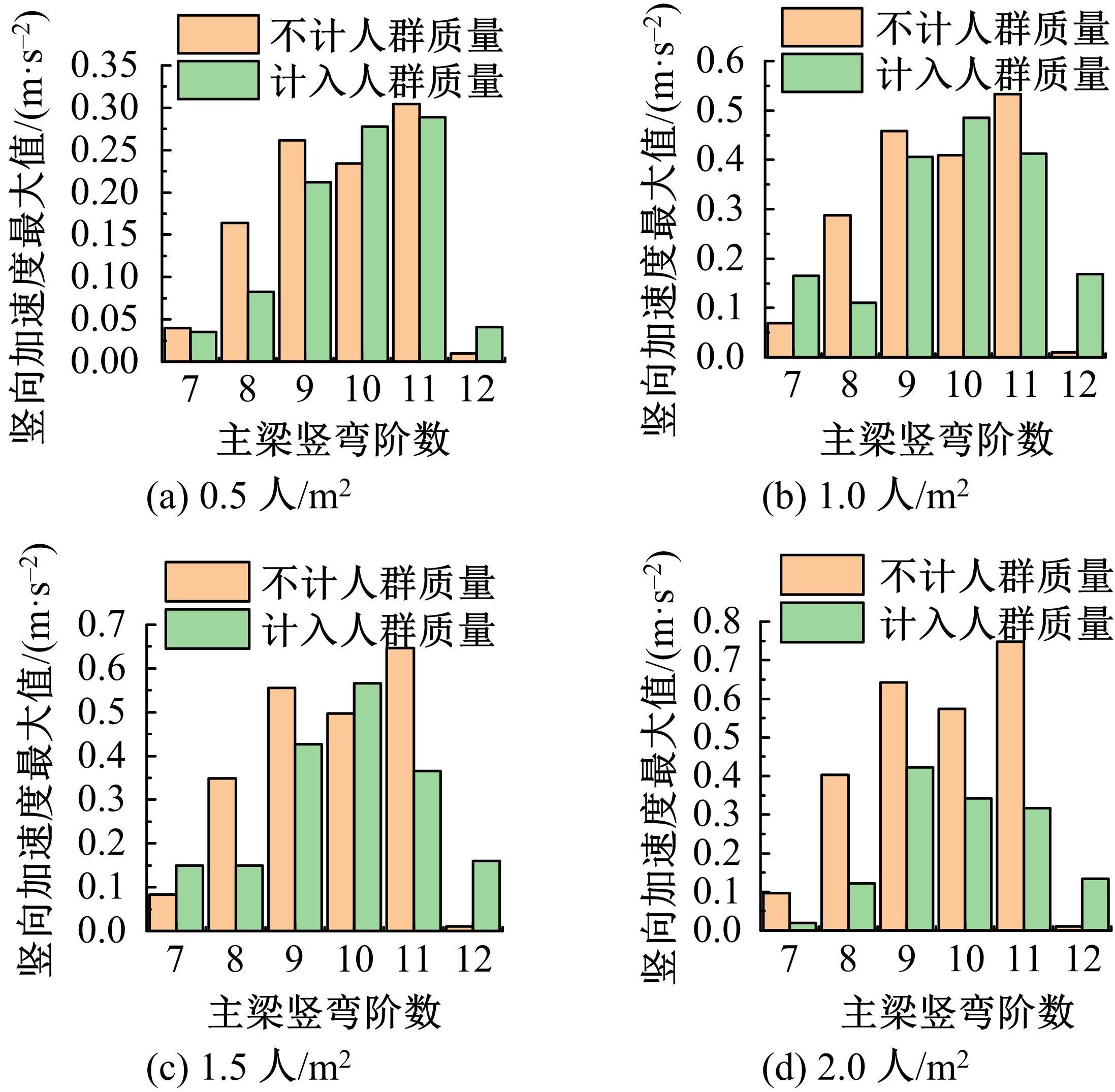
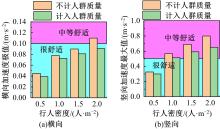
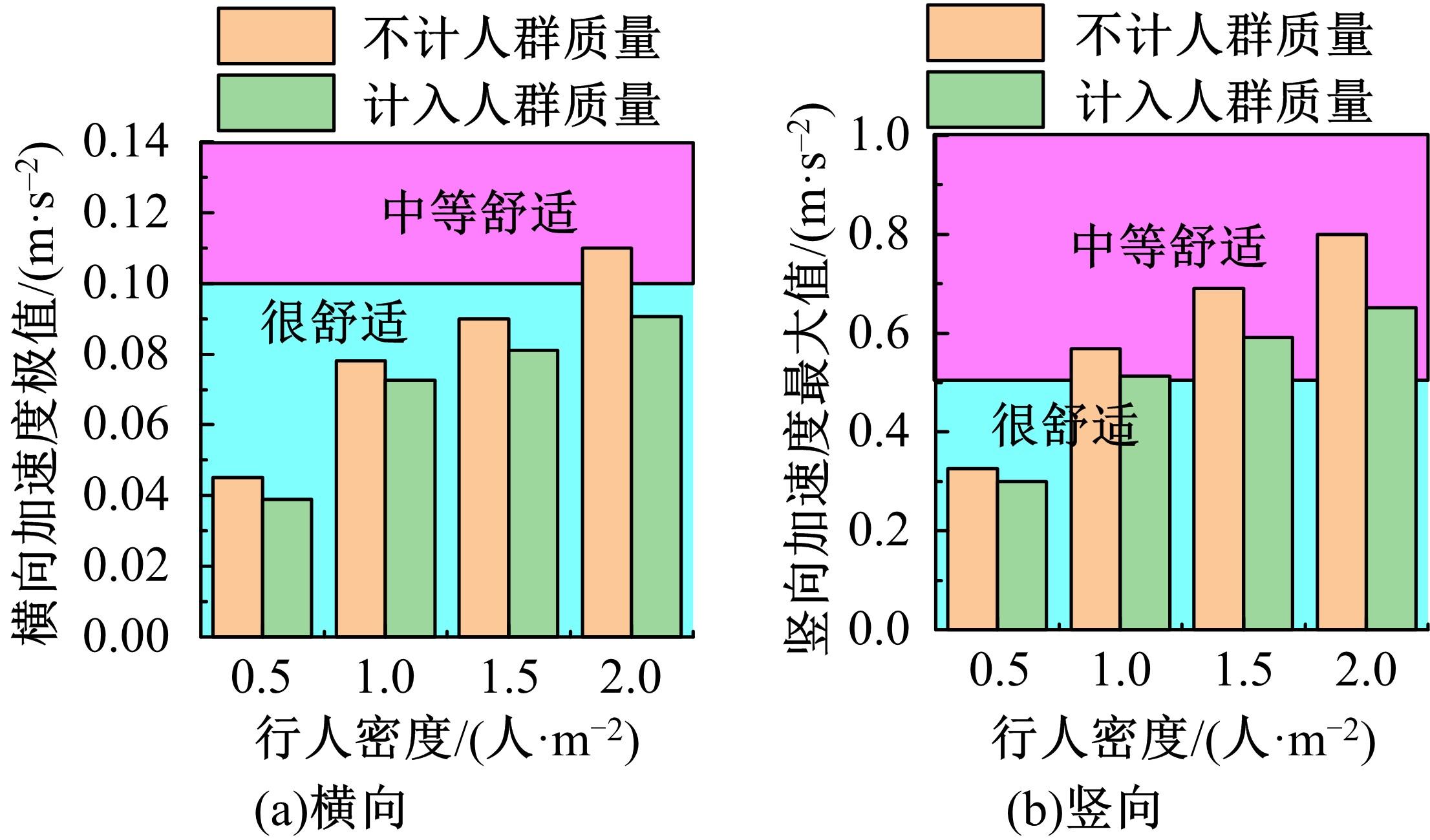
Journal of Jilin University(Engineering and Technology Edition) ›› 2022, Vol. 52 ›› Issue (11): 2644-2652.doi: 10.13229/j.cnki.jdxbgxb20210393
Human⁃induced vibration analysis and pedestrian comfort evaluation for suspension footbridge with different hunger systems
Yan-ling ZHANG1,2( ),Can WANG1,2,Xu ZHANG1,2,Ang-yang WANG3,Yun-sheng LI1,2(
),Can WANG1,2,Xu ZHANG1,2,Ang-yang WANG3,Yun-sheng LI1,2( )
)
- 1.School of Civil Engineering,Shijiazhuang Tiedao University,Shijiazhuang 050043,China
2.Key Laboratory of Roads and Railway Engineering Safety Control of Ministry of Education,Shijiazhuang Tiedao University,Shijiazhuang 050043,China
3.Cangzhou Power Supply Branch of State Grid Hebei Electric Power Co. ,Ltd. ,Cangzhou 061000,China
CLC Number:
- U448.25
| 1 | 陈舟, 颜全胜, 贾布裕, 等. 行走激励下人行桥振动响应简化计算[J]. 哈尔滨工程大学学报, 2018, 39(3): 483-489. |
| Chen Zhou, Yan Quan-sheng, Jia Bu-yu, et al. Simplified calculation on the vibration response of a footbridge under human walking loads[J]. Journal of Harbin Engineering University, 2018, 39(3): 483-489. | |
| 2 | 李泽民,吴冬雁,刘宣含,等. 真实步伐荷载作用下人行桥振动及共振加速分析[J]. 噪声与振动控制, 2019, 39(6): 164-168. |
| Li Ze-min, Wu Dong-yan, Liu Xuan-han, et al. Vibration and resonance response analysis of footbridges under actual walking load[J]. Noise and Vibration Control, 2019, 39(6): 164-168. | |
| 3 | 汪志昊,寇琛,刘召朋,等. 人体姿态对人-结构耦合系统竖向动力特性影响试验研究[J]. 振动与冲击,2019, 38(19): 58-63. |
| Wang Zhi-hao, Kou Chen, Liu Zhao-peng, et al. Tests for effects of human body posture on vertical dynamic characteristics of a human- structure interaction system[J]. Jounal of Vibation and Shock, 2019, 38(19): 58-63. | |
| 4 | 谢伟平,汤宗恒,何卫. 多人-桥竖向动力相互作用研究[J]. 振动与冲击, 2020, 39(11): 76-82. |
| Xie Wei-ping, Tang Zong-heng, He Wei. Study on vertical vibration of bridge-pedestrians dynamic interaction system[J]. Journal of Vibration and Shock, 2020, 39(11): 76-82. | |
| 5 | 张琼, 南娜娜, 朱前坤, 等. 基于社会力模型的人群-桥梁竖向动力耦合效应研究[J]. 振动与冲击,2020, 39(9): 71-79. |
| Zhang Qiong, Na-na Nan, Zhu Qian-kun, et al. Analysis on the vertical coupled dynamic effect of a crowd-bridge system based on the social force model [J]. Journal of Vibration and Shock, 2020, 39(9):71-79. | |
| 6 | 操礼林,吕亚兵,曹栋,等. 行人动力学参数对大跨简支人行桥人致振动的影响分析[J]. 东南大学学报: 自然科学版, 2020, 50(2): 260-266. |
| Cao Li-lin, Ya-bing Lyu, Cao Dong, et al. Influence analysis of pedestrian dynamic parameters on human- induced vibration of long span simply supported footbridge[J]. Journal of Southeast University(Natural Science Edition), 2020, 50(2): 260-266. | |
| 7 | 王晋平,熊杰程,陈隽.人群步行荷载的互谱模型及应用[J]. 土木工程学报, 2020, 53(7): 12-20. |
| Wang Jin-ping, Xiong Jie-cheng, Chen Jun. Cross-spectral model for crowd walking load and its application[J]. China Civil Engineering Journal, 2020, 53(7): 12-20. | |
| 8 | 贾布裕,颜全胜,余晓琳,等. 考虑行人随机性的人行桥人致横向振动稳定性分析[J]. 工程力学, 2019, 36(1): 155-164. |
| Jia Bu-yu, Yan Quan-sheng, Yu Xiao-lin, et al. Stability analysis on pedestrian-induced lateral vibration of footbridges considering pedestrian stochastic excitation[J]. Engineering Mechanics, 2019, 36(1): 155-164. | |
| 9 | Han H, Zhou D, Ji T, et al. Modelling of lateral forces generated by pedestrians walking across footbridges[J]. Applied Mathematical Modelling, 2021, 89: 1775-1791. |
| 10 | Lai E, Gentile C, Mulas M G. Experimental and numerical serviceability assessment of a steel suspension footbridge[J]. Journal of Constructional Steel Research, 2017, 132: 16-28. |
| 11 | Bedon C. Diagnostic analysis and dynamic identification of a glass suspension footbridge via on-site vibration experiments and FE numerical modeling[J]. Composite Structures, 2019, 216: 366-378. |
| 12 | Bedon C. Experimental investigation on vibration sensitivity of an indoor glass footbridge to walking conditions[J]. Journal of Building Engineering, 2020, 29: 1-17. |
| 13 | 邹卓,宋旭明,李璋,等. 基于TMD的自锚式人行悬索桥人致振动控制研究[J]. 铁道科学与工程学报, 2018, 15(10): 2574-2582. |
| Zou Zhuo, Song Xu-ming, Li Zhang, et al. Study of pedestrian-induced vibration of self-anchored suspension footbridge based on TMD[J]. Journal of Railway Science and Engineering, 2018, 15(10): 2574-2582. | |
| 14 | Dong C Z, Bas S, Catbas N. Investigation of vibration serviceability of a footbridge using computer vision-based methods[J]. Engineering Structures, 2020, 224: 1-13. |
| 15 | Pampa D, Sriram N, Scott W. Reliability-based assessment and calibration of standards for the lateral vibration of pedestrian bridges[J]. Engineering Structures, 2021, 239: 1-13. |
| 16 | Research Fund for Coal and Steel, HiVoSS: Design of Footbridges [S]. |
| 17 | 王保群,张强勇,张凯,等. 自锚式斜拉-悬吊协作体系桥梁动力性能[J]. 吉林大学学报: 工学版, 2009, 39(3): 686-690. |
| Wang Bao-qun, Zhang Qiang-yong, Zhang Kai, et al. Dynamic characteristics for self-anchored cable-stayed suspension bridges[J]. Journal of Jilin University(Engineering and Technology Edition), 2009, 39(3): 686-690. | |
| 18 | 钟昌均,王忠彬,柳晨阳.悬索桥主索鞍承载力影响因素及结构优化[J]. 吉林大学学报: 工学版, 2021, 51(6): 2068-2078. |
| Zhong Chang-jun, Wang Zhong-bin, Liu Chen-yang. Influencing factors and structural optimization of main cable saddle bearing capacity of suspension bridge[J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(6): 2068-2078. |
| [1] | Hua-wen YE,Zhi-chao DUAN,Ji-lin LIU,Yu ZHOU,Bing HAN. Wheel⁃load diffusion effect on orthotropic steel⁃concrete composite bridge deck [J]. Journal of Jilin University(Engineering and Technology Edition), 2022, 52(8): 1808-1816. |
| [2] | Li-feng WANG,Zi-wang XIAO,Sai-sai YU. New risk analysis method based on Bayesian network for hanging basker system of multi-tower cable-stayed bridge [J]. Journal of Jilin University(Engineering and Technology Edition), 2022, 52(4): 865-873. |
| [3] | Chang-jun ZHONG,Zhong-bin WANG,Chen-yang LIU. Influencing factors and structural optimization of main cable saddle bearing capacity of suspension bridge [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(6): 2068-2078. |
| [4] | Wei CHEN,Tian-bao WAN,Zhong-bin WANG,Xuan LI,Rui-li SHEN. Design and performance of internal air supply conduit for dehumidification in main cables of suspension bridges [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(5): 1749-1755. |
| [5] | Shu-lun GUO,Tie-yi ZHONG,Zhi-gang YAN. Calculation method of buffeting response for stay cables of long⁃span cable⁃stayed bridge [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(5): 1756-1762. |
| [6] | Kai GAO,Gang LIU. Effective strength improvement of global critical strength branch and bound method [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(2): 597-603. |
| [7] | Ya-feng GONG,Jia-xiang SONG,Guo-jin TAN,Hai-peng BI,Yang LIU,Cheng-xin SHAN. Multi⁃vehicle bridge weigh⁃in⁃motion algorithm [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(2): 583-596. |
| [8] | Qing-wen KONG,Guo-jin TAN,Long-lin WANG,Yong WANG,Zhi-gang WEI,Han-bing LIU. Analysis of free vibration characteristics of cracked box girder bridge based on finite element method [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(1): 225-232. |
| [9] | Hua CHEN,Yao-jia CHEN,Bin XIE,Peng-kai WANG,Lang-ni DENG. Interface failure mechanism and bonding strength calculation of CFRP tendons bonded anchorage system [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(5): 1698-1708. |
| [10] | Ya-feng GONG,Jia-xiang SONG,Hai-peng BI,Guo-jin TAN,Guo-hai HU,Si-yuan LIN. Static test and finite element analysis of scale model of fabricated box culvert [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(5): 1728-1738. |
| [11] | Hao GAO,Jun-jie WANG,Hui-jie LIU,Jian-ming WANG. Design criterion and applied devices for controlled seismic behavior of continuous girder bridges [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(5): 1718-1727. |
| [12] | Qian-hui PU,Jing-wen LIU,Gang-yun ZHAO,Meng YAN,Xiao-bin LI. Theoretical analysis of bearing capacity of concrete eccentric compressive column reinforced by HTRCS [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(2): 606-612. |
| [13] | Yun-long ZHANG,Yang-yang GUO,Jing WANG,Dong LIANG. Natural frequency and mode of vibration of steel⁃concrete composite beam [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(2): 581-588. |
| [14] | Bo-xin WANG,Hai-tao YANG,Qing WANG,Xin GAO,Xiao-xu CHEN. Bridge vibration signal optimization filtering method based on improved CEEMD⁃multi⁃scale permutation entropy analysis [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(1): 216-226. |
| [15] | Miao ZHANG,Yong-jiu QIAN,Fang ZHANG,Shou-qin ZHU. Experimental analysis of spatial force performance of concrete-reinforced stone arch bridge based on enlarged section method [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(1): 210-215. |
|
||