基于改进鲸鱼算法优化SVM参数和特征选择

doi:10.13229/j.cnki.jdxbgxb.20211348

吉林大学学报(工学版) ›› 2023, Vol. 53 ›› Issue (10): 2952-2963.doi: 10.13229/j.cnki.jdxbgxb.20211348

基于改进鲸鱼算法优化SVM参数和特征选择

郭辉^1,²(),付接递^1,²,李振东^1,²(),严岩³,李虓^1,²

^1.宁夏大学信息工程学院，银川 750021
^2.宁夏大数据与人工智能省部共建协同创新中心，银川 750021
^3.国网宁夏电力有限公司电力科学研究院，银川 750011

收稿日期:2021-12-07 出版日期:2023-10-01 发布日期:2023-12-13
通讯作者: 李振东 E-mail:gh606@163.com;lizhendong@nxu.edu.cn
作者简介:郭辉（1975-），男，副教授，博士. 研究方向：人工智能，智能监控. E-mail：gh606@163.com
基金资助:
宁夏自然科学基金项目(2021AAC03035)

SVM parameters and feature selection optimization based on improved whale algorithm

Hui GUO^1,²(),Jie-di FU^1,²,Zhen-dong LI^1,²(),Yan YAN³,Xiao LI^1,²

^1.School of Information Engineering，Ningxia University，Yinchuan 750021，China
^2.Collaborative Innovation Center for Ningxia Big Data and Artificial Intelligence Co-founded by Ningxia Municipality and Ministry of Education，Yinchuan 750021，China
^3.Electric Power Research Institute，State Grid Ningxia Power Co. ，Ltd. ，Yinchuan 750011，China

Received:2021-12-07 Online:2023-10-01 Published:2023-12-13
Contact: Zhen-dong LI E-mail:gh606@163.com;lizhendong@nxu.edu.cn

摘要/Abstract

摘要：

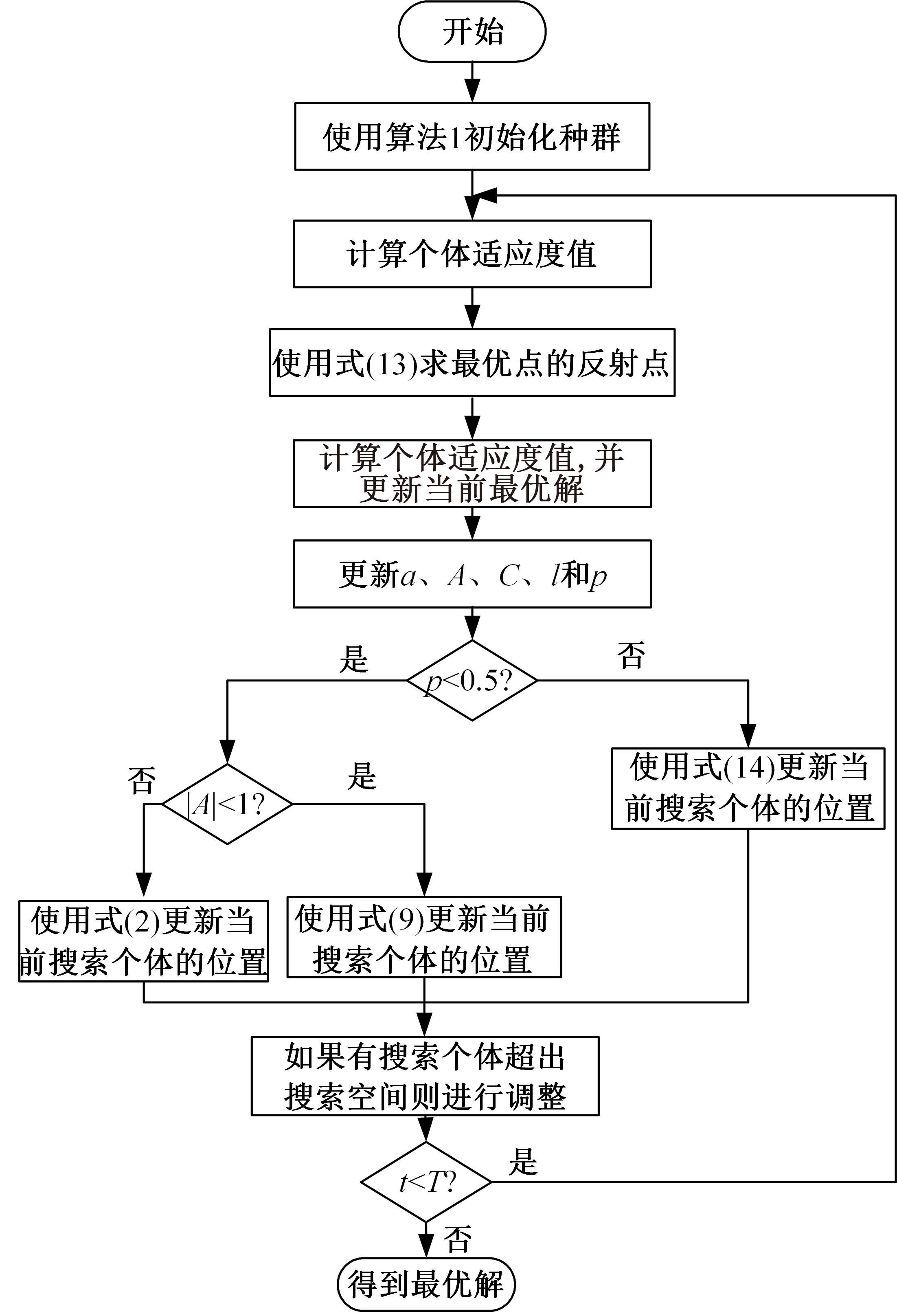
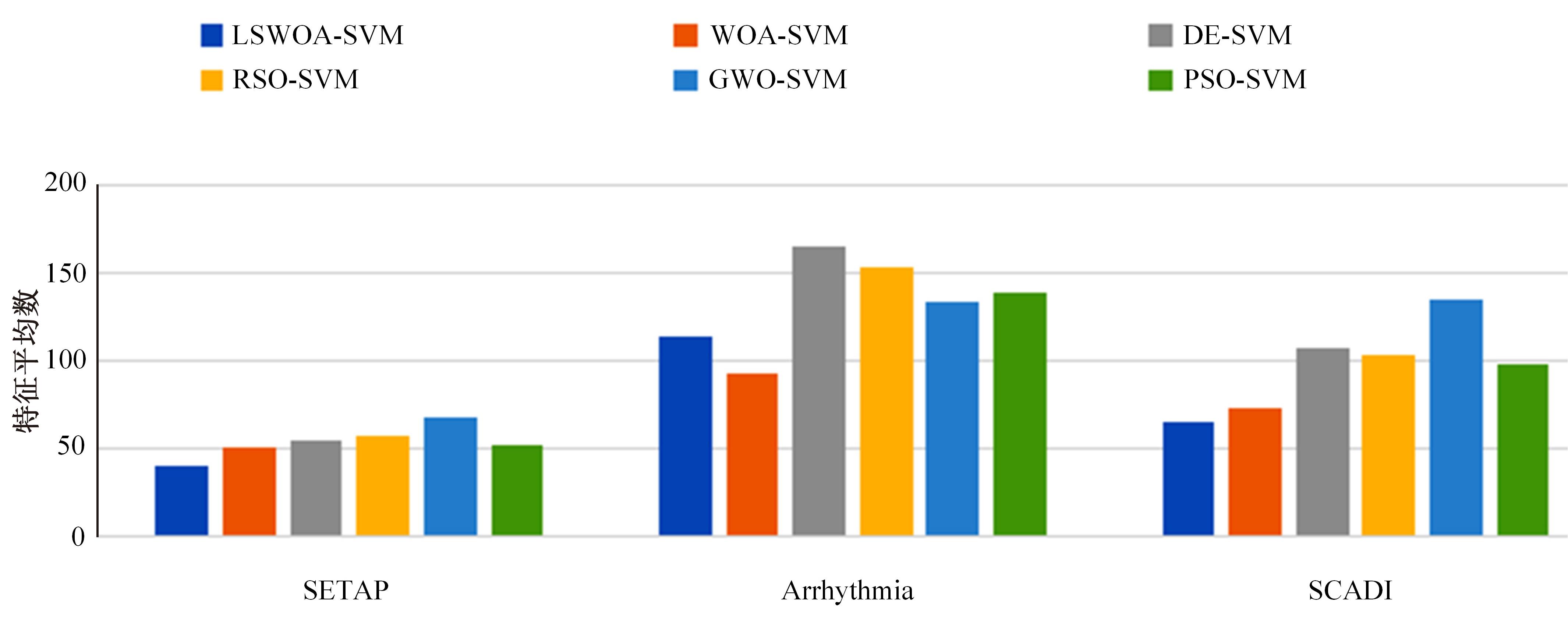
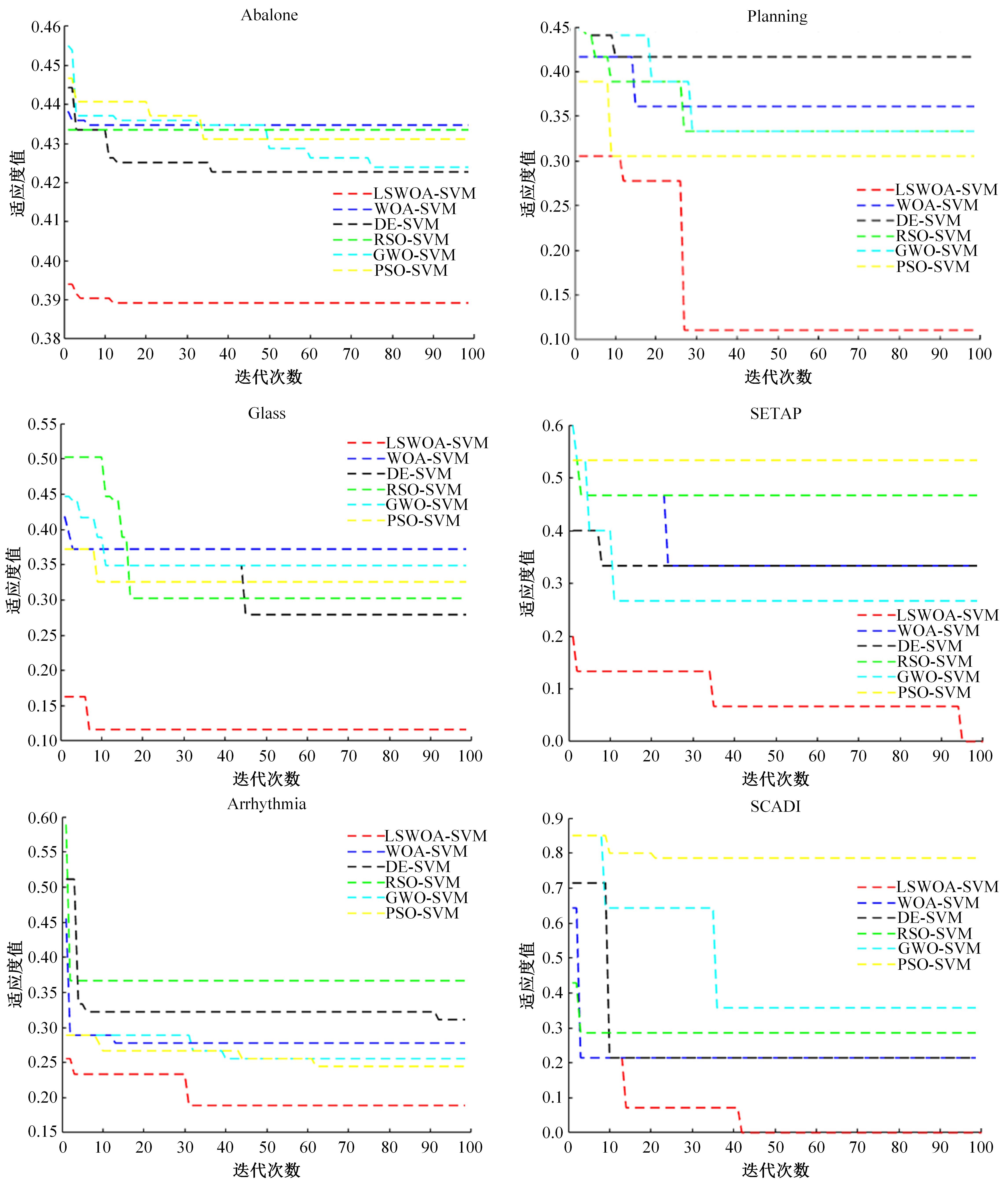
针对传统支持向量机（SVM）在数据分类方面准确率识别较低的问题，提出了一种改进鲸鱼优化算法同步优化SVM的特征选择模型。首先，利用Levy飞行策略对鲸鱼优化算法的螺旋更新位置进行变异扰动，利用单纯形策略中的反射操作对种群中的精英个体进行反射点求解的改进，标准函数的测试结果证明其改进能有效提高算法的收敛速度和计算精度；其次，将SVM核参数和特征选择目标作为共同优化对象，在获得最优核参数的同时得到相对应的最优特征子集；最后，对UCI标准数据集和真实乳腺癌数据集进行特征选择仿真实验，在平均分类准确率、平均适应度值、适应度标准差和所选特征个数上进行评价。结果表明，本文算法在降低特征维度，实现数据分类上效果明显。在真实乳腺癌数据集上的分类精度与传统支持向量机相比提高了11.053%。

关键词: 鲸鱼优化算法, 特征选择, 单纯形, Levy飞行, SVM, 数据分类

Abstract:

Prevalent scenario of support vector machine （SVM） in data classification exists the low recognition accuracy problems， this paper proposes a feature selection model for synchronous optimization of SVM with improved Whale optimization algorithm. Firstly， the Levy flight strategy was used to perturb the spiral update position of the whale optimization algorithm and the reflection operation of the simplex method to improve the reflection point solution of the elite individuals in the population. With extensive empirical validations on standard function， the proposed method can effectively improve the convergence speed and calculation accuracy. Secondly， SVM kernel parameters and feature selection targets were the co-optimization objects effect for obtaining the optimal kernel parameters and the corresponding optimal feature subset. Finally， feature selection simulation experiments were conducted on UCI standard data set and real breast cancer data set， and the average classification accuracy， average fitness value， fitness standard deviation and the number of selected features were evaluated and analyzed. Compared with traditional support vector machines， the classification accuracy of real breast cancer data set is improved by 11.053%.

Key words: whale optimization algorithm, feature selection, simplex, levy flight, SVM, data classification

中图分类号:

TP301.6

郭辉,付接递,李振东,严岩,李虓. 基于改进鲸鱼算法优化SVM参数和特征选择[J]. 吉林大学学报(工学版), 2023, 53(10): 2952-2963.

Hui GUO,Jie-di FU,Zhen-dong LI,Yan YAN,Xiao LI. SVM parameters and feature selection optimization based on improved whale algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(10): 2952-2963.

图/表 14

图1

图2

图3

图4

表1

表2

不同算法的初始化参数"

算法	参数
WOA	随机数 $r 、 p ∈ [0,1]$ ，收敛因子 $a ∈ [0,2]$ ，常数b=1，随机数 $l = [- 1,1]$
LSWOA	随机数 $r 、 p ∈ [0,1]$ ，收敛因子 $a ∈ [0,2]$ ，常数b=1，随机数 $l = [- 1,1]$ ，反射系数 $α = 1$ ，扩展系数 $γ = 2$ ，收缩系数 $β = 0.5$ ，指数系数 $ζ ∈ (1,3]$ ，常数 $τ = 1.5$ ，步长缩放因子 $η = 1$
GWO	随机数 $r 1 、 r 2 ∈ [0,1]$ ，收敛因子 $a ∈ [0,2]$
PSO	学习因子 $c 1 = c 2 = 2$ ，惯性因子 $ω = 0.6$ ，速度 $v ∈ [- 1,1]$
DE	交叉概率 $C R = 0.2$ ，缩放因子 $β ∈ [0.2,0.8]$
RSO	开发参数C=［0，2］，勘探参数A=［0，2］，随机变量R = ［1，2］

表2

表3

图5

图6

表4

表5

图7

表6

表7

参考文献 31

1	Meenakshi S. Improving the performance of heart disease classification using chaotic tent map based whale optimizer for feature selection with SVM algorithm[J]. Turkish Journal of Physiotherapy and Rehabilitation,2021, 32(3): 4229-4244.
2	Antal B, Hajdu A. An ensemble-based system for automatic screening of diabetic retinopathy[J]. Knowledge-based Systems, 2014, 60: 20-27.
3	Phuong T M, Lin Z, Altman R B. Choosing SNPs using feature selection[C]∥IEEE Computational Systems Bioinformatics Conference,Stanford, USA, 2005: 301-309.
4	Hamla H, Ghanem K. Comparative study of embedded feature selection methods on microarray data[C]∥IFIP International Conference on Artificial Intelligence Applications and Innovations, Hersonissos, Greece, 2021: 69-77.
5	Blum Christian, Roli Andrea. Metaheuristics in combi-natorial optimization: overview and conceptual comparison[J]. ACM Comput Surv, 2003, 35(3): 268-308.
6	Mirjalili S, Mirjalili S M, Lewis A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61.
7	Kennedy J, Eberhart R. Particle swarm optimization[C]∥Proceedings of International Conference on Neural Networks, Perth, Australia, 1995: 1942-1948.
8	Wong K P, Dong Z Y. Differential evolution, an alternative approach to evolutionary algorithm[C]∥Proceedings of the 13th International Conference on, Intelligent Systems Application to Power Systems, Arlington, USA, 2005: 73-83.
9	Dhiman G, Kaur A. STOA: a bio-inspired based optimization algorithm for industrial engineering problems[J]. Engineering Applications of Artificial Intelligence, 2019, 82: 148-174.
10	Zhang Y, Gong D, Cheng J. Multi-objective particle swarm optimization approach for cost-based feature selection in classification[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2015, 14(1): 64-75.
11	Sayed G I, Darwish A, Hassanien A E. A new chaotic whale optimization algorithm for features selection[J]. Journal of Classification, 2018, 35(2): 300-344.
12	张文杰, 蒋烈辉. 一种基于遗传算法优化的大数据特征选择方法[J]. 计算机应用研究, 2020, 37(1): 50-52, 56.
	Zhang Wen-jie, Jiang Lie-hui. A feature selection method for big data based on genetic algorithm optimization[J]. Computer Application Research, 2020, 37(1): 50-52, 56.
13	Mirjalili S, Saremi S, Mirjalili S M, et al. Multi-objective grey wolf optimizer: a novel algorithm for multi-criterion optimization[J]. Expert Systems with Applications, 2016, 47: 106-119.
14	贾鹤鸣, 李瑶, 孙康健. 基于遗传乌燕鸥算法的同步优化特征选择[J]. 自动化学报, 2022, 48(6): 1601-1615.
	Jia He-ming, Li Yao, Sun Kang-jian. Synchronous optimization feature selection based on Genetic Black-tern algorithm[J]. Automatica, 2022, 48(6): 1601-1615.
15	沈永良, 宋杰, 万志超. 基于改进烟花算法的SVM特征选择和参数优化[J]. 微电子学与计算机, 2018, 35(1): 21-25.
	Shen Yong-liang, Song Jie, Wan Zhi-chao. SVM feature selection and parameter optimization based on improved fireworks algorithm[J]. Microelectronics and Computers, 2018, 35(1): 21-25.
16	姚全珠, 蔡婕. 基于PSO的LS-SVM特征选择与参数优化算法[J]. 计算机工程与应用, 2010, 46(1): 134-136, 229.
	Yao Quan-zhu, Cai Jie. LS-SVM Feature selection and parameter optimization algorithm based on PSO[J]. Computer Engineering and Applications, 2010, 46(1): 134-136, 229.
17	Mirjalili S, Lewis A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67.
18	Mafarja Majdi M, Seyedali Mirjalili. Hybrid whale optimization algorithm with simulated annealing for feature selection[J]. Neurocomputing, 2017, 260: 302-312.
19	Jadhav Amolkumar Narayan, Gomathi N. WGC: hybridzation of exponential grey wolf optimizer with whale optimization for data clustering[J]. Alexandria Engineering Journal, 2018, 57: 1569-1584.
20	Yan Z, Zhang J, Zeng J, et al. Nature-inspired approach: an enhanced whale optimization algorithm for global optimization[J]. Mathematics and Computers in Simulation, 2021, 185: 17-46.
21	龙文, 蔡绍洪, 焦建军, 等. 求解大规模优化问题的改进鲸鱼优化算法[J]. 系统工程理论与实践, 2017, 37(11): 2983-2994.
	Long Wen, Cai Shao-hong, Jiao Jian-jun, et al. Improved whale optimization algorithm for solving large scale optimization problems[J]. Systems Engineering Theory and Practice, 2017, 37(11): 2983-2994.
22	Zhang Y, Zhang Y, Wang G, et al. An improved hybrid whale optimization algorithm based on differential evolution[C]∥International Conference on Artificial Intelligence and Electromechanical Automation (AIEA), Tianjin, China, 2020: 103-107.
23	毕孝儒, 牟琦, 龚尚福. 融合动态概率阈值和自适应变异的鲸鱼优化算法[J]. 微电子学与计算机, 2019, 36(12): 78-83.
	Bi Xiao-ru, Mou Qi, Gong Shang-fu. Whale optimization algorithm combining dynamic probability threshold and adaptive variation[J]. Microelectronics and Computers, 2019, 36(12): 78-83.
24	Shi X, Li M. Whale optimization algorithm improved effectiveness analysis based on compound chaos optimization strategy and dynamic optimization parameters[C]∥International Conference on Virtual Reality and Intelligent Systems, Jishou, China, 2019: 338-341.
25	Mostafa Bozorgi S, Yazdani S. IWOA: an improved whale optimization algorithm for optimization problems[J]. Journal of Computational Design and Engineering, 2019, 6(3): 243-259.
26	Zamli K Z. Optimizing S-box generation based on the adaptive agent heroes and cowards algorithm[J]. Expert Systems with Applications, 2021,182: No.115305.
27	Nelder J A, Mead R. A simplex method for function minimization[J]. The Computer Journal, 1965, 7(4): 308-313.
28	郭德龙, 周锦程, 周永权. 基于Levy飞行改进蝴蝶优化算法[J]. 数学的实践与认识, 2021, 51(12): 130-137.
	Guo De-long, Zhou Jin-cheng, Zhou Yong-quan. Improved butterfly optimization algorithm based on Levy flight[J]. Practice and Understanding of Mathematics, 2021, 51(12): 130-137.
29	Aljarah I, Al-Zoubi A M, Faris H, et al. Simultaneous feature selection and support vector machine optimization using the grasshopper optimization algorithm[J]. Cognitive Computation, 2018, 10(2): 478-495.
30	Dua D, Graff C. UCI machine learning repository[R]. Irvine: University of California, School of Information and Computer Science, 2019.
31	Blake C. UCI repository of machine learning databases[DB/OL].[2020-07-04]. .

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

序号	数据集	特征个数	样本个数	类别数
1	Abalone	8	4177	3
2	Planning	12	182	2
3	Glass	10	214	6
4	SETAP	102	74	2
5	Arrhythmia	279	452	16
6	SCADI	205	70	6

数据集	LSWOA-SVM	WOA-SVM	DE-SVM	RSO-SVM	GWO-SVM	PSO-SVM	SVM
Abalone	58.231 536 93	57.828 343 31	58.143 712 60	56.918 163 67	58.099 800 40	57.788 423 20	53.640 718 56
Planning	79.166 666 67	73.981 481 48	73.703 703 70	72.129 629 63	76.111 111 11	75.092 592 59	57.222 222 22
Glass	76.744 186 05	74.418 604 65	74.883 720 93	73.643 410 85	74.418 604 65	72.945 736 43	66.589 147 29
SETAP	93.111 111 11	78.000 000 00	79.111 111 11	74.222 222 22	80.666 666 67	53.266 666 67	54.222 222 22
Arrhythmia	79.074 074 10	73.555 555 56	70.777 777 78	70.148 148 15	75.910 000 00	76.400 000 00	33.615 047 62
SCADI	84.047 619 05	82.619 047 62	80.238 095 24	78.333 333 33	81.428 571 43	37.380 952 38	46.904 761 90

数据集	LSWOA-SVM	WOA-SVM	DE-SVM	RSO-SVM	GWO-SVM	PSO-SVM
Abalone	0.413 534 868	0.417 540 235	0.414 421 412	0.426 546 846	0.414 843 643	0.417 951 277
Planning	0.206 288 056	0.257 623 889	0.260 375 833	0.275 943 333	0.236 542 778	0.246 637 222
Glass	0.230 259 966	0.253 290 999	0.248 697 089	0.260 945 788	0.253 295 073	0.267 877 209
SETAP	0.083 609 547	0.217 824 272	0.206 853 107	0.255 206 602	0.191 426 440	0.420 250 421
Arrhythmia	0.207 214 421	0.261 833 118	0.289 359 379	0.295 536 010	0.238 520 717	0.233 689 842
SCADI	0.157 937 271	0.174 459 791	0.195 695 085	0.214 508 130	0.212 160 776	0.619 976 506

数据集	LSWOA-SVM	WOA-SVM	DE-SVM	RSO-SVM	GWO-SVM	PSO-SVM
Abalone	0.011 671 204	0.015 791 320	0.003 578 256	0.012 751 977	0.011 699 578	0.007 107 340
Planning	0.056 415 932	0.057 459 254	0.074 715 987	0.057 451 324	0.056 623 350	0.062 293 555
Glass	0.033 731 524	0.049 733 523	0.054 607 824	0.050 202 946	0.051 482 396	0.034 393 867
SETAP	0.053 713 194	0.096 625 241	0.083 018 551	0.110 092 820	0.070 986 415	0.080 800 224
Arrhythmia	0.009 876 514	0.019 347 746	0.030 610 446	0.063 172 914	0.020 095 432	0.014 849 456
SCADI	0.070 778 772	0.062 548 304	0.085 021 358	0.071 844 929	0.100 004 803	0.096 068 102

算法	1	2	3	4	5	6	7	8	9	10	平均值
SVM	71.92	70.17	68.42	71.92	72.50	68.62	69.93	67.67	73.81	71.24	70.62
LSWOA-SVM	80.70	80.19	78.94	80.70	85.96	78.43	80.70	84.21	85.96	80.94	81.67
WOA-SVM	68.42	82.45	80.70	68.42	77.56	77.35	78.35	70.46	66.35	80.72	75.078
DE-SVM	82.45	77.19	68.42	80.70	70.17	75.43	73.68	71.92	75.46	71.98	74.74
RSO-SVM	71.92	77.19	73.68	78.94	71.92	77.19	78.94	68.42	73.68	68.56	74.04
GWO-SVM	78.94	77.19	75.43	71.92	77.19	78.94	78.94	75.43	71.92	71.92	75.78
PSO-SVM	64.91	77.19	70.17	80.70	75.43	76.56	72.13	66.14	81.56	76.42	74.12

基于改进鲸鱼算法优化SVM参数和特征选择

SVM parameters and feature selection optimization based on improved whale algorithm

RICH HTML

PDF (PC)

摘要/Abstract

引用本文

使用本文

图/表 14

参考文献 31

相关文章 15

Metrics

本文评价

推荐阅读 0

序号	c/q	分类准确率/%	选择特征个数	适应度值
1	8.4514/0.1957	80.70	4	0.1911
2	1.2511/1.8087	77.19	5	0.2259
3	0.8659/0.4986	78.94	4	0.2085
4	5.3472/5.5680	80.70	4	0.1911
5	0.3845/0.5476	85.96	5	0.1391
6	0.3015/0.2212	75.43	4	0.2433
7	36.0582/1.2499	80.70	4	0.1911
8	23.498/0.9358	84.21	4	0.1564
9	24.5493/0.0141	85.96	6	0.1391
10	20.2506/2.6024	78.94	4	0.2085

[1]	周丰丰,颜振炜. 基于混合特征的特征选择神经肽预测模型[J]. 吉林大学学报(工学版), 2023, 53(11): 3238-3245.
[2]	白丽丽,姜封国,周玉明,曾枭. 基于改进鲸鱼算法的结构可靠性优化设计[J]. 吉林大学学报(工学版), 2023, 53(11): 3160-3165.
[3]	李佩泽,赵世舜,翁小辉,蒋鑫妹,崔洪博,乔建磊,常志勇. 基于多传感器优化的农药残留快速检测新方法[J]. 吉林大学学报(工学版), 2022, 52(8): 1951-1956.
[4]	周丰丰,朱海洋. 基于三段式特征选择策略的脑电情感识别算法SEE[J]. 吉林大学学报(工学版), 2022, 52(8): 1834-1841.
[5]	王斌,何丙辉,林娜,王伟,李天阳. 基于随机森林特征选择的茶园遥感提取[J]. 吉林大学学报(工学版), 2022, 52(7): 1719-1732.
[6]	王生生,姜林延,杨永波. 基于最优传输特征选择的医学图像分割迁移学习[J]. 吉林大学学报(工学版), 2022, 52(7): 1626-1638.
[7]	姚引娣,贺军瑾,李杨莉,谢荡远,李英. 自构建改进型鲸鱼优化BP神经网络的ET₀模拟计算[J]. 吉林大学学报(工学版), 2021, 51(5): 1798-1807.
[8]	李景彬,杨禹锟,温宝琴,坎杂,孙雯,杨朔. 基于根茬检测的秋后残膜回收导航路径提取方法[J]. 吉林大学学报(工学版), 2021, 51(4): 1528-1539.
[9]	高万夫,张平,胡亮. 基于已选特征动态变化的非线性特征选择方法[J]. 吉林大学学报(工学版), 2019, 49(4): 1293-1300.
[10]	赵东,孙明玉,朱金龙,于繁华,刘光洁,陈慧灵. 结合粒子群和单纯形的改进飞蛾优化算法[J]. 吉林大学学报(工学版), 2018, 48(6): 1867-1872.
[11]	刘杰, 张平, 高万夫. 基于条件相关的特征选择方法[J]. 吉林大学学报(工学版), 2018, 48(3): 874-881.
[12]	袁哲明, 张弘杨, 陈渊. 基于特征选择和支持向量机的HIV-1型蛋白酶剪切位点预测[J]. 吉林大学学报(工学版), 2017, 47(2): 639-646.
[13]	代琨，于宏毅，仇文博，李青. 基于SVM的网络数据无监督特征选择算法[J]. 吉林大学学报(工学版), 2015, 45(2): 576-582.
[14]	王刚, 张禹瑄, 李颖, 陈慧灵, 胡玮通, 秦磊. 一种微阵列数据降维新方法[J]. 吉林大学学报(工学版), 2014, 44(5): 1429-1434.
[15]	李阳, 文敦伟, 王珂, 刘乐. 多核学习矩阵化最小二乘支持向量机算法及肺结节识别[J]. 吉林大学学报(工学版), 2014, 44(2): 508-515.