减震结构阻尼器优化布置混合算法

doi:10.13229/j.cnki.jdxbgxb.20221255

摘要/Abstract

摘要：

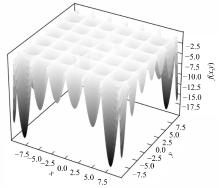
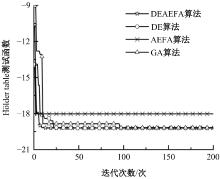
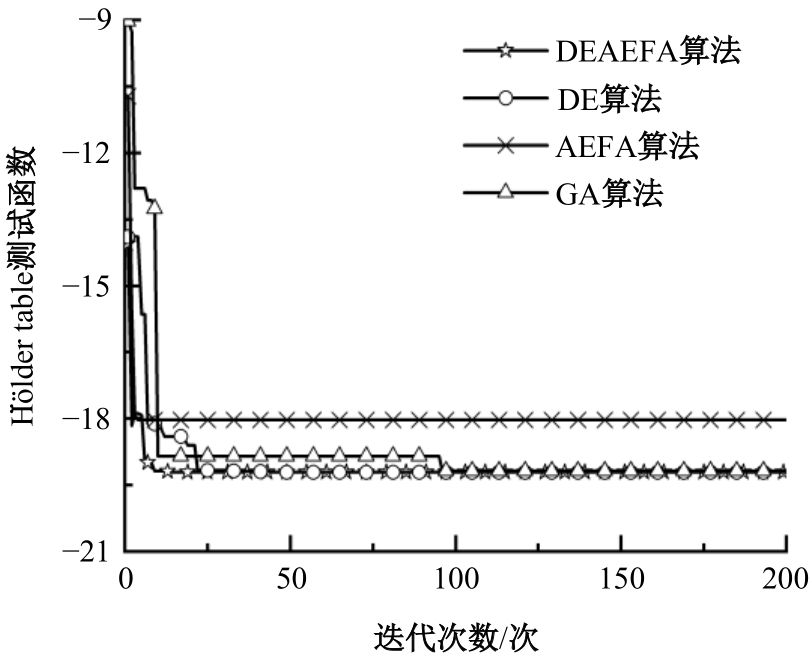
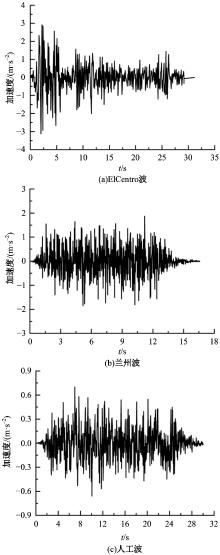
为提高现有减震结构阻尼器优化布置计算效率和性能，提出了一种差分进化和人工电场混合算法。该算法采用Tent混沌映射初始化改善种群分布质量和多样性，引入变异交叉选择机制维持种群中优势个体的进化避免趋于局部最优。通过测试函数算例和混凝土框架结构的阻尼器优化布置算例，对比各优化算法的寻优计算性能及收敛速度。研究结果表明：差分进化和人工电场混合算法具有较好的全局寻优能力，收敛速度快，优化后结构减震性能好。

关键词: 结构工程, 差分进化算法, 人工电场算法, 混合算法, 减震结构, 阻尼器优化布置

Abstract:

To improve the computational efficiency and performance of the existing algorithms of arrangement optimization of dampers in energy dissipation structures， a hybrid algorithm of differential evolution and artificial electric field was proposed. This algorithm utilizes Tent chaotic mapping initialization to improve the quality and diversity of population distribution， and introduces a mutation cross selection mechanism to maintain the evolution of dominant individuals in the population and avoid approaching local optimum. Through a test function example and an arrangement optimization example of dampers of concrete frame structure， the optimization performance and convergence speed of various optimization algorithms were compared. The research results indicate that the hybrid algorithm of differential evolution and artificial electric field has good global optimization ability， fast convergence speed， and the optimized structure has good seismic damping performance.

Key words: structural engineering, differential evolution algorithm, artificial electric field algorithm, hybrid algorithm, energy dissipation structures, damper optimal layout

中图分类号:

TU375.4

阎奇武,邹忠亮. 减震结构阻尼器优化布置混合算法[J]. 吉林大学学报(工学版), 2024, 54(8): 2267-2274.

Qi-wu YAN,Zhong-liang ZOU. Hybrid algorithm for seismic energy-dissipated structures based on optimal placement of dampers[J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(8): 2267-2274.

图/表 6

图1

图2

图3

图4

表1

图5

参考文献 26

1	贾毅, 赵人达, 王永宝, 等. 多跨长联连续梁桥粘滞阻尼器参数敏感性分析[J]. 吉林大学学报: 工学版,2019, 49(6): 1871-1883.
	Jia Yi, Zhao Ren-da, Wang Yong-bao, et al. Sensitivity analysis of viscous damper parameters for multi⁃span and long⁃unit continuous girder bridges[J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(6): 1871-1883.
2	马芳武, 韩丽, 吴量, 等. 基于遗传与粒子群算法的隔振平台减振性能优化[J]. 吉林大学学报: 工学版, 2020,50(5):1608-1616.
	Ma Fang-wu, Han Li, Wu Liang, et al. Damping optimization of heavy⁃loaded anti⁃vibration platform based on genetic algorithm and particle swarm algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(5): 1608-1616.
3	Kaleybar R S, Tehrani P. Effects of using different arrangements and types of viscous dampers on seismic performance of intermediate steel moment frames in comparison with different passive dampers[J]. Structures, 2021, 33: 3382-3396.
4	朱林,苏振超,薛艳霞. 基于层间平均位移比的粘滞阻尼器布置方法[J]. 厦门理工学院学报, 2020, 28(3): 58-61.
	Zhu Lin, Su Zhen-chao, Xue Yan-xia. Viscous damper arrangement method based on average displacement ratio between layers and its application[J]. Journal of Xiamen Institute of Technology, 2020, 28(3): 58-61.
5	韩建平, 俞兆藩. 减震结构黏滞阻尼器优化布置方案的比较[J].甘肃科学学报, 2016, 28(6): 52-57.
	Han Jian-ping, Yu Zhao-fan. Comparison of optimized layout schemes of viscous damper with shock absorbing structure[J]. Journal of Gansu Sciences, 2016, 28(6): 52-57.
6	Takewaki I. Building Control with Passive Dampers Optimal Performance-Based Design for Earthquakes[M]. Singapore: John Wiley & Sons (Asia), 2009.
7	燕乐纬, 陈洋洋, 王龙, 等. 基于相对适应度遗传算法的高层结构粘滞阻尼器优化布置[J]. 振动与冲击, 2014, 33(6): 195-200.
	Yan Le-wei, Chen Yang-yang, Wang Long, et al. Optimum installation of viscous dampers in tall buildings based on relative fitness genetic algorithm[J]. Vibration and Shock, 2014, 33(6): 195-200.
8	Sonmez M, Aydin E, Karabork T. Using an artificial bee colony algorithm for the optimal placement of viscous dampers in planar building frames[J]. Structural and Multidisciplinary Optimization, 2013, 48: 395-409.
9	Çerçevik A E, Avşar Ö, Dilsiz A. Optimal placement of viscous wall dampers in RC moment resisting frames using metaheuristic search methods[J]. Engineering Structures, 2021, 249:113108.
10	Yan J, Downey A, Cancelli A, et al. Concrete crack detection and monitoring using a capacitive dense sensor array[J]. Sensors, 2019, 19(8): 1843.
11	Zhang Z, Yan J, Li L, et al. Condition assessment of stay cables through enhanced time series classification using a deep learning approach[J]. Smart Structures and Systems, 2022, 29(1): 105-116.
12	Zou Z, Yan Q. Artificial intelligence algorithm-based arrangement optimization of structural isolation bearings[J]. Applied Sciences, 2022, 12(24): 122412629.
13	Yan J, Laflamme S, Leifsson L. Computational framework for dense sensor network evaluation based on model-assisted probability of detection[J]. Materials Evaluation, 2020, 78(5): 573-583.
14	Gao W, Liu S. A modified artificial bee colony algorithm[J]. Computers & Operations Research,2012, 39(3): 687-697.
15	Gandomi A H, Yang X S. Chaotic bat algorithm[J]. Journal of Computational Science, 2014, 5(2): 224-232.
16	Cui X, Li Y, Fan J, et al. A hybrid improved dragonfly algorithm for feature selection[J]. IEEE Access, 2020, 8: 155619-155629.
17	Storn R, Price K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359.
18	Yadav A. AEFA: artificial electric field algorithm for global optimization[J]. Swarm and Evolutionary Computation, 2019, 48: 93-108.
19	许小健, 黄小平, 钱德玲. 自适应加速差分进化算法[J].复杂系统与复杂性科学, 2008, 5(1):87-92.
	Xu Xiao-jian, Huang Xiao-ping, Qian De-ling. Adaptive accelerated differential evolution algorithm[J]. Complex Systems and Complexity Science, 2008, 5(1): 87-92.
20	李晓瑜.一种改进的人工电场算法[J]. 计算机与数字工程,2022, 50(1): 18-22.
	Li Xiao-yu. An improved artificial electric field algorithm[J]. Computer and Digital Engineering, 2022, 50(1): 18-22.
21	赵欣. 不同一维混沌映射的优化性能比较研究[J].计算机应用研究, 2012, 29(3): 913-915.
	Zhao Xin. Research on optimization performance comparison of different one-dimensional chaotic maps[J]. Application Research of Computers, 2012, 29(3): 913-915.
22	邹忠亮. 型钢再生混凝土框架抗震机理与地震易损性分析[D]. 长沙: 中南大学土木工程学院, 2021.
	Zou Zhong-liang. Seismic mechanism and seismic vulnerability analysis of recycled steel reinforced concrete frame[D]. Changsha: School of Civil Engineering, Central South University, 2021.
23	. 建筑消能减震技术规程 [S].
24	. 高层建筑混凝土结构技术规程 [S].
25	曲激婷. 位移型和速度型阻尼器减震对比研究及优化设计[D]. 大连: 大连理工大学土木工程学院, 2008.
	Qu Ji-ting. Studies on seismic behavior comparison and optimal design of displacement-based and velocity-based dampers[D]. Dalian: School of Civil Engineering of Dalian University of Technology, 2008.
26	. 建筑抗震设计规范 [S].

相关文章 15

[1]	闫云娟,查伟雄,石俊刚,严丽平. 基于随机充电需求的充电桩优化双层模型[J]. 吉林大学学报(工学版), 2024, 54(8): 2238-2244.
[2]	姜封国,周玉明,白丽丽,梁爽. 改进磷虾群算法及其在结构优化中的应用[J]. 吉林大学学报(工学版), 2024, 54(8): 2256-2266.
[3]	张广泰,周乘孝,刘诗拓. 盐渍土环境下纤维锂渣混凝土柱恢复力模型[J]. 吉林大学学报(工学版), 2024, 54(7): 1944-1957.
[4]	刁延松,任义建,杨元强,赵凌云,刘秀丽,刘芸. 带有摩擦耗能组件的可更换钢梁柱拼接节点抗震性能试验[J]. 吉林大学学报(工学版), 2024, 54(6): 1643-1656.
[5]	樊学平,刘月飞. 基于改进高斯混合粒子滤波新算法的桥梁极值应力动态预测[J]. 吉林大学学报(工学版), 2024, 54(4): 1038-1044.
[6]	刘一凡,缪志伟,申晨,耿祥东. 基于蒙特卡罗法的不均匀锈蚀钢筋力学性能评估[J]. 吉林大学学报(工学版), 2024, 54(4): 1007-1015.
[7]	樊学平,周衡,刘月飞. 基于Gaussian Copula-贝叶斯动态模型的桥梁构件时变可靠性分析[J]. 吉林大学学报(工学版), 2024, 54(2): 485-493.
[8]	范亮,徐英铭,谭阳. 集束群钉式装配组合梁界面滑移计算[J]. 吉林大学学报(工学版), 2023, 53(9): 2533-2541.
[9]	樊学平,周衡,刘月飞. 桥梁时变可靠性的多过程贝叶斯动态混合预测[J]. 吉林大学学报(工学版), 2023, 53(8): 2332-2338.
[10]	熊二刚,巩忠文,罗佳明,范团结. 基于数字图像相关技术的钢筋混凝土梁裂缝试验[J]. 吉林大学学报(工学版), 2023, 53(4): 1094-1104.
[11]	王晓东,李宁静,李强. 高压脉冲放电破碎混凝土梁试验[J]. 吉林大学学报(工学版), 2023, 53(2): 496-504.
[12]	匡亚川,陈立斌,李超举,贺宇豪. 栓钉剪力连接件力学性能分析[J]. 吉林大学学报(工学版), 2023, 53(2): 538-546.
[13]	戴理朝,周亮,杨晓文,王磊. 基于Connector单元的锈蚀RC梁界面粘结性能细观数值模拟[J]. 吉林大学学报(工学版), 2023, 53(10): 2886-2896.
[14]	褚云朋,孙鑫晖,李明,姚勇,黄汉杰. 下击暴流作用下圆形马鞍面屋盖风压特性[J]. 吉林大学学报(工学版), 2022, 52(8): 1826-1833.
[15]	姚勇,苏留锋,李明,褚云朋,黄汉杰. 下击暴流作用下双面球壳型屋面风载特性[J]. 吉林大学学报(工学版), 2022, 52(3): 615-625.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

算法	阻尼器布置（1~13层）	最大层间位移角	最大加速度/（m·s^-2）	目标函数值
AEFA	3-3-1-4-0-3-2-4-1-2-3-0-0	0.005 51	3.035	0.870 1
DEAEFA	0-3-4-1-4-0-1-0-4-3-2-1-3	0.004 97	2.854	0.853 3
GA	2-1-5-1-3-1-3-5-0-0-2-2-1	0.005 46	2.950	0.857 1
DE	1-4-2-4-1-4-0-1-3-2-1-1-2	0.005 17	3.001	0.855 3
无控结构	—	0.007 91	3.215	—