吉林大学学报(工学版) ›› 2021, Vol. 51 ›› Issue (2): 728-737.doi: 10.13229/j.cnki.jdxbgxb20191174
• 通信与控制工程 • 上一篇
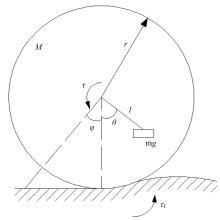
球形机器人的自适应分数阶PIλDμ滑模速度控制方法
- 北京交通大学 机械与电子控制工程学院,北京 100044
Adaptive fractional PIλDμ sliding mode control method for speed control of spherical robot
Ting ZHOU( ),Yu-gong XU,Bin WU(
),Yu-gong XU,Bin WU( )
)
- School of Mechanical,Electronic and Control Engineering,Beijing Jiaotong University,Beijing 100044,China
摘要:
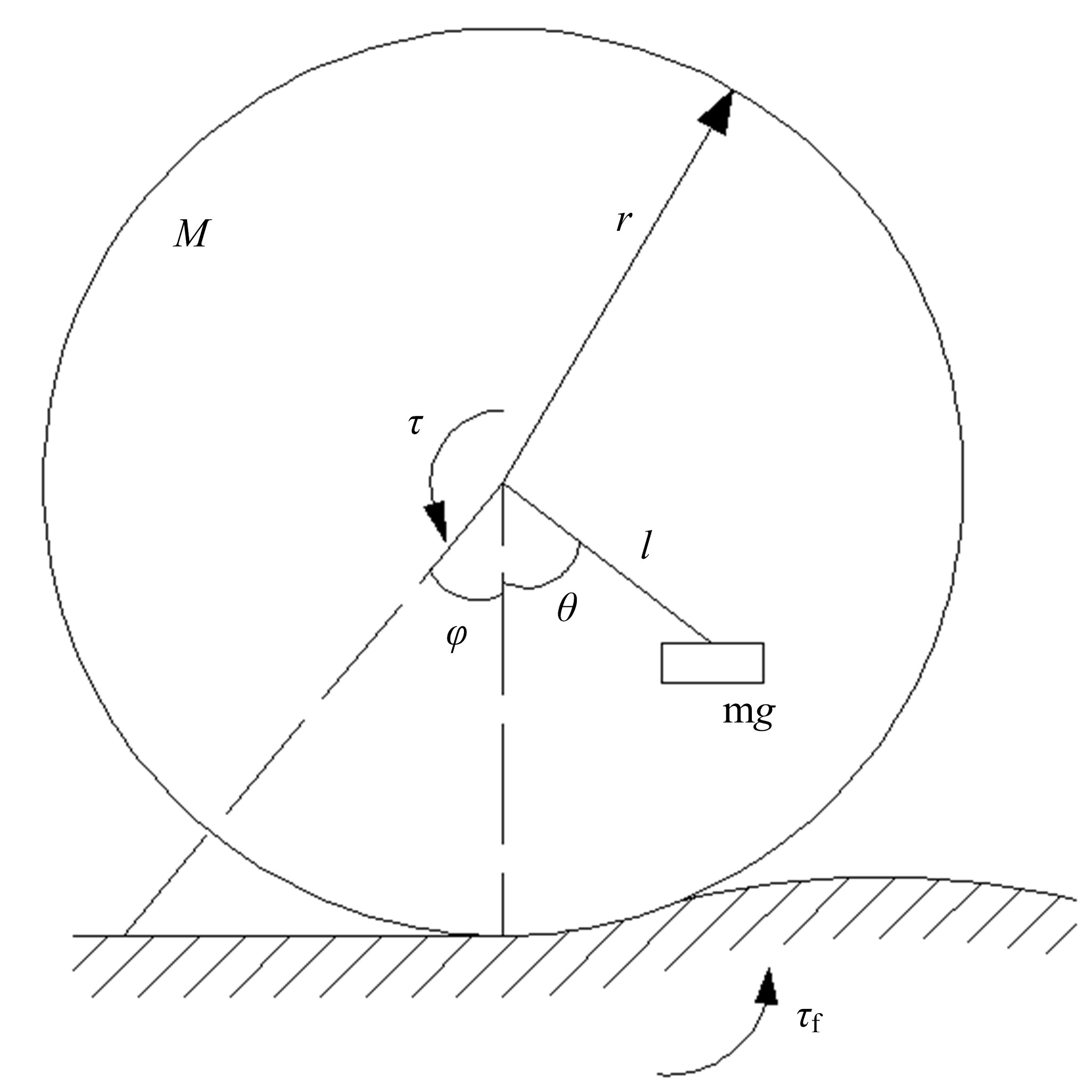
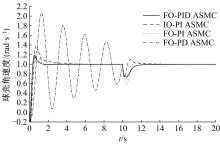
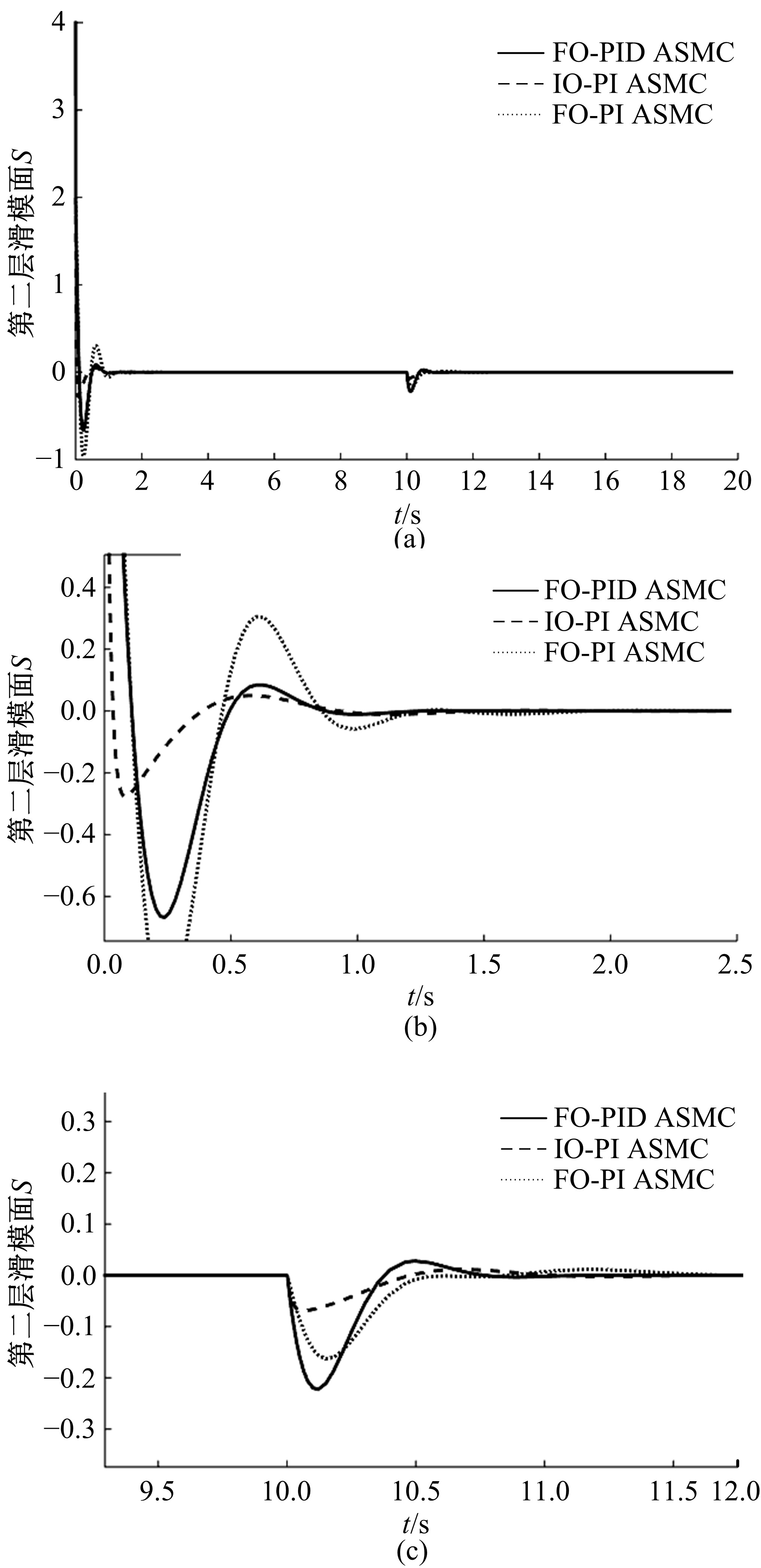
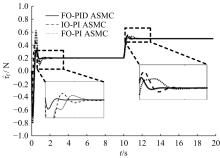
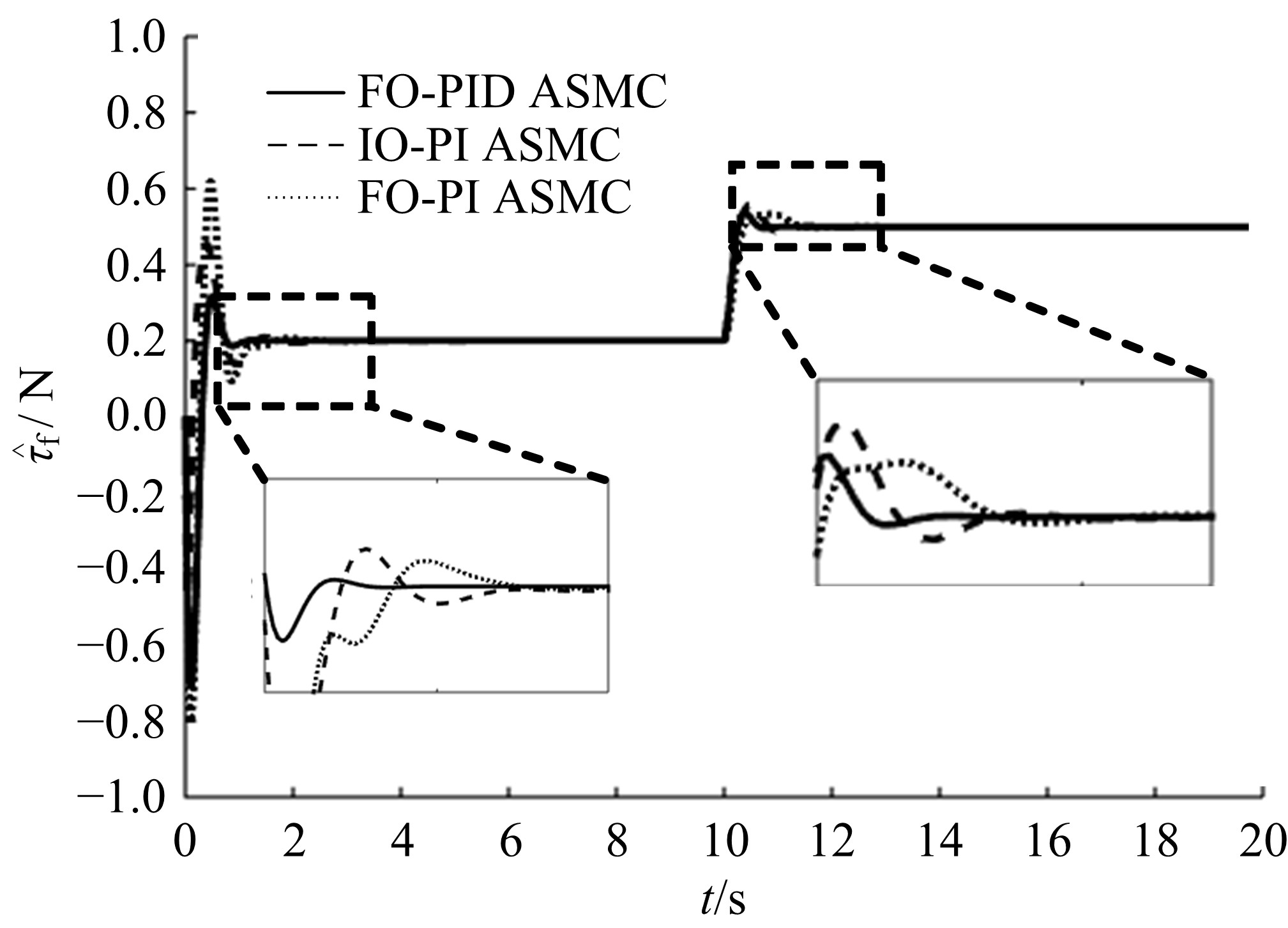
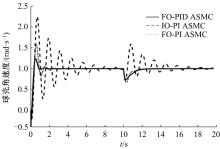
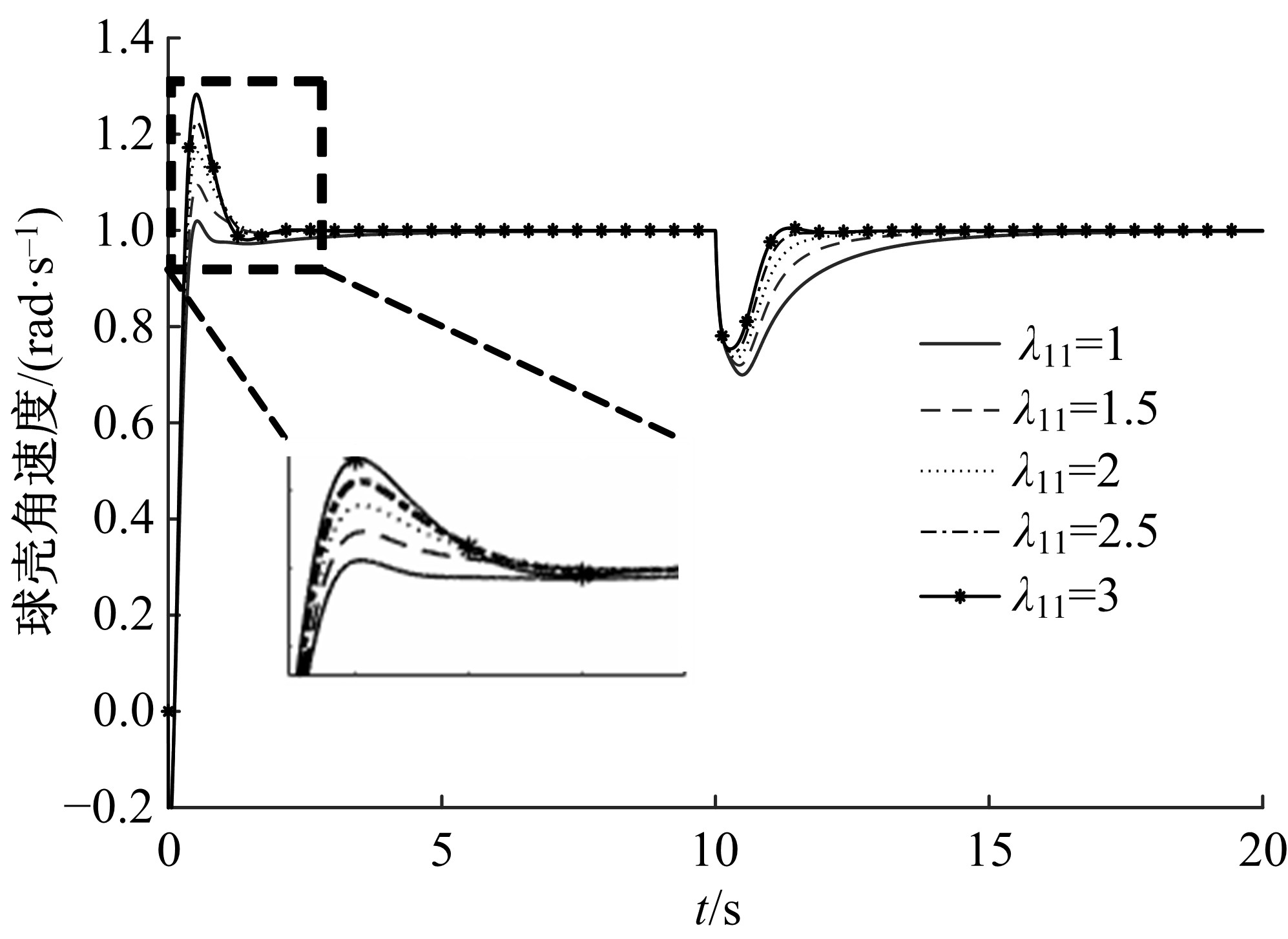
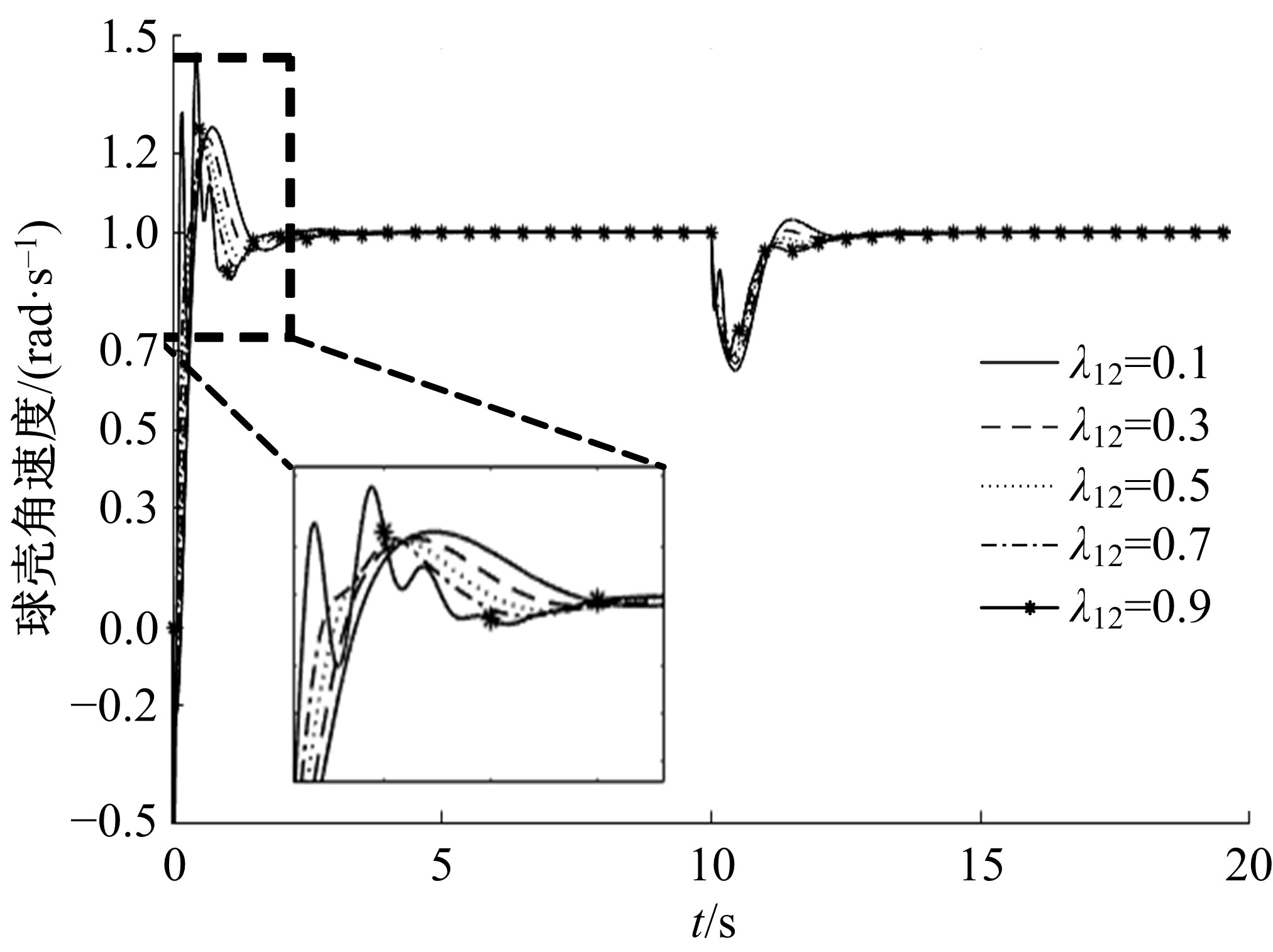
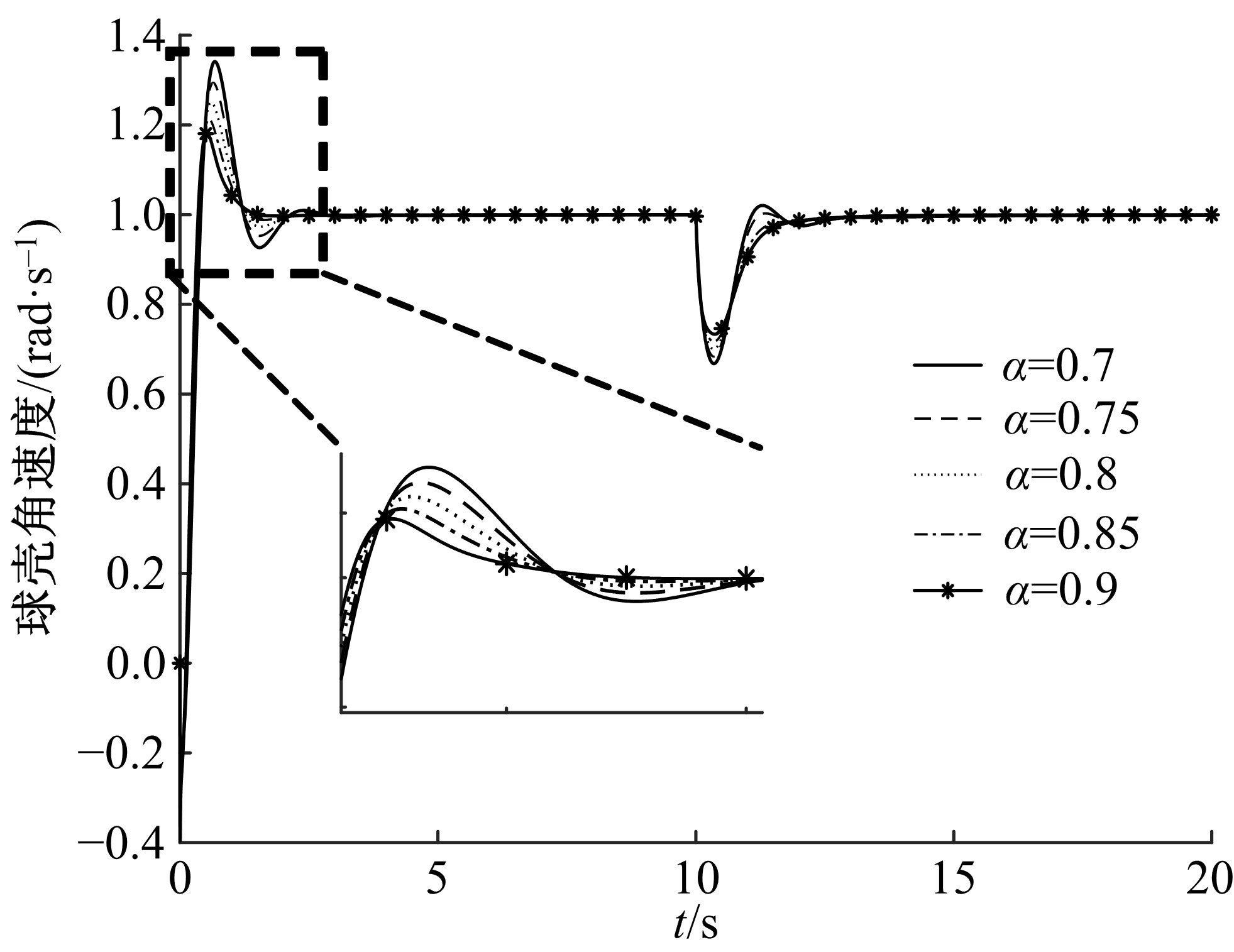
为解决传统分层滑模控制方法应用于球形机器人速度控制中会出现调节时间长、超调量大的问题,通过在滑模面内引入微分环节并结合分数阶微积分,提出一种具有分数阶PIλDμ结构的滑模面,并给了该滑模面渐近稳定的参数选取条件。基于该分数阶PIλDμ滑模面设计了球形机器人直线运动速度控制器,并通过自适应算法实现了对未知滚动摩擦阻力的实时估计。仿真结果表明:相比传统分层滑模控制方法,本文自适应分数阶滑模控制方法能有效减少控制过程中的超调,并且具有更短的调节时间,能对未知滚动摩擦阻力进行准确的估计,在存在系统参数摄动的情况下具有更好的鲁棒性。
中图分类号:
- TP242.3
| 1 | Zhan Q, Cai Y, Yan C X. Design, analysis and experiments of an omni-directional spherical robot[C]∥2011 IEEE International Conference on Robotics and Automation, Piscataway, United States, 2011: 9-13. |
| 2 | Mattias S, Mathias B, Alessandro S, et al. An autonomous spherical robot for security tasks[C]∥Proceedings of the 2006 IEEE International Conference on Computational Intelligence for Homeland Security and Personal Safety, Piscataway, United States, 2006: 51-55. |
| 3 | Wang H Q, Liu P X, Xie X J, et al. Adaptive fuzzy asymptotical tracking control of nonlinear systems with unmodeled dynamics and quantized actuator[J/OL].[2018-04-03]. |
| 4 | Liu D L, Sun H X, Jia Q X. A family of spherical mobile robot: driving ahead motion control by feedback linearization [C]∥2008 2nd International Symposium on Systems and Control in Aerospace and Astronautics, Piscataway, United States, 2008: 1-6. |
| 5 | Lin C M, Mon Y J. Decoupling control by hierarchical fuzzy sliding-mode controller[J]. IEEE Transactions on Control Systems Technology, 2005, 13(4):593-598. |
| 6 | Wu Y M, Sun N, Chen H, et al. Nonlinear time-optimal trajectory planning for varying-rope-length overhead cranes[J]. Assembly Automation, 2018, 38(5): 587-594. |
| 7 | Yang C G, Li Z J, Cui R X, et al. Neural network-based motion control of an underactuated wheeled inverted pendulum model[J]. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(11): 2004-2016. |
| 8 | Cai Y, Zhan Q, Xi X. Neural network control for the linear motion of a spherical mobile robot[J]. International Journal of Advanced Robotic Systems, 2011, 8(4): 79-87. |
| 9 | Utkin V. Variable structure systems with sliding modes[J]. IEEE Transactions on Automatic Control, 1977, 22(2): 212-222. |
| 10 | Xu R, Ümit Ö. Sliding mode control of a class of underactuated systems[J]. Automatica, 2008, 44(1): 233-241. |
| 11 | Lo J C, Kuo Y H. Decoupled fuzzy sliding-mode control[J]. IEEE Transactions on Fuzzy Systems, 2002, 6(3): 426-435. |
| 12 | 韩京元, 田彦涛, 孔英秀, 等. 板球系统自适应解耦滑模控制[J]. 吉林大学学报: 工学版, 2014, 44(3): 718-725. |
| Han Jing-yuan, Tian Yan-tao, Kong Ying-xiu, et al. Adaptive decoupled sliding mode control for the ball and plate system[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(3):718-725. | |
| 13 | Wang W, Yi J Q, Zhao D B, et al. Design of a stable sliding-mode controller for a class of second-order underactuated systems[J]. IEE Proceedings: Control Theory and Applications, 2004, 151(6): 683-690. |
| 14 | Barambones O, Aitor J G, Francisco J M. Integral sliding-mode controller for induction motor based on field-oriented control theory [J]. IET Control Theory and Applications, 2007, 1(3): 786-794. |
| 15 | Yue M, Liu B Y. Adaptive control of an underactuated spherical robot with a dynamic stable equilibrium point using hierarchical sliding mode approach[J]. International Journal of Adaptive Control and Signal Processing, 2014, 28(6): 523-535. |
| 16 | Yue M, Liu B Y, An C, et al. Extended state observer-based adaptive hierarchical sliding mode control for longitudinal movement of a spherical robot[J]. Nonlinear Dynamics, 2014, 78(2): 1233-1244. |
| 17 | Eker I. Sliding mode control with PID sliding surface and experimental application to an electromechanical plant[J]. Isa Transactions, 2006, 45(1): 109-118. |
| 18 | Igor P. Fractional-order systems and PID controllers[J]. IEEE Transactions on Automatic Control, 1999, 44(1): 208-214. |
| 19 | Ebrahimkhani S. Robust fractional order sliding mode control of doubly-fed induction generator (DFIG)-based wind turbines[J]. Isa Transactions, 2016, 63: 343-354. |
| 20 | Zhang B T, Pi Y G, Luo Y. Fractional order sliding-mode control based on parameters auto-tuning for velocity control of permanent magnet synchronous motor [J]. ISA Transactions, 2012, 51(5): 649-656. |
| 21 | 黄家才, 施昕昕, 李宏胜, 等. 永磁同步电机调速系统的分数阶积分滑模控制[J]. 吉林大学学报: 工学版, 2014, 44(6): 1736-1742. |
| Huang Jia-cai, Shi Xin-xin, Li Hong-sheng, et al. Speed control of PMSM using fractural order integral sliding mode controller[J]. Journal of Jilin University(Engineering and Technology Edition), 2014, 44(6): 1736-1742. | |
| 22 | Yue M, Deng Z Q, Yu X Y, et al. Introducing hit spherical robot: dynamic modeling and analysis based on decoupled subsystem[C]∥2006 IEEE International Conference on Robotics and Biomimetics, Piscataway, United States, 2006: 181-186. |
| 23 | Igor P. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications[M]. Amsterdam, The Netherlands: Elsevier, 1998. |
| 24 | Qian D L, Li C P, Agarwal R P, et al. Stability analysis of fractional differential system with riemann-liouville derivative[J]. Mathematical and Computer Modelling and International Journal, 2010, 52(5): 862-874. |
| 25 | Kibas A A, Srivastava H M, Trujillo J J. Theory and Applications of Fractional Differential Equations[M]. Amsterdam, The Netherlands: Elsevier Science Limited, 2006. |
| 26 | Deng W H, Li C P, Lu J H. Stability analysis of linear fractional differential system with multiple time delays[J]. Nonlinear Dynamics, 2007, 48(4): 409-416. |
| 27 | Tao G. A simple alternative to the Barbalat lemma[J]. IEEE Transactions on Automatic Control, 1997,42(5): 698. |
| 28 | Boiko I M. Analysis of chattering in sliding mode control systems with continuous boundary layer approximation of discontinuous control[C]∥Proceedings of the 2011 American Control Conference, Piscataway, United States, 2011: 757-762. |
| [1] | 马彦,黄健飞,赵海艳. 基于车间通信的车辆编队控制方法设计[J]. 吉林大学学报(工学版), 2020, 50(2): 711-718. |
| [2] | 王伟,赵健廷,胡宽荣,郭永仓. 基于快速非奇异终端滑模的机械臂轨迹跟踪方法[J]. 吉林大学学报(工学版), 2020, 50(2): 464-471. |
| [3] | 顾万里,王萍,胡云峰,蔡硕,陈虹. 具有H∞性能的轮式移动机器人非线性控制器设计[J]. 吉林大学学报(工学版), 2018, 48(6): 1811-1819. |
| [4] | 李志慧, 夏英集, 曲昭伟, 任景琛. 视频监控的数据驱动背景模型[J]. 吉林大学学报(工学版), 2017, 47(4): 1286-1294. |
| [5] | 王春阳, 辛瑞昊, 史红伟. 针对大滞后系统的滞后时间削弱自抗扰控制方法[J]. 吉林大学学报(工学版), 2017, 47(4): 1231-1237. |
| [6] | 邵克勇, 陈丰, 王婷婷, 王季驰, 周立朋. 无平衡点分数阶混沌系统全状态自适应控制[J]. 吉林大学学报(工学版), 2017, 47(4): 1225-1230. |
| [7] | 邓丽飞, 石要武, 朱兰香, 于丁力. SI发动机闭环系统故障检测[J]. 吉林大学学报(工学版), 2017, 47(2): 577-582. |
| [8] | 李兵强, 陈晓雷, 林辉, 吕帅帅, 马冬麒. 机电伺服系统高精度自适应反推滑模控制[J]. 吉林大学学报(工学版), 2016, 46(6): 2003-2009. |
| [9] | 曹福成, 邢笑雪, 李元春, 赵希禄. 下肢康复机器人轨迹自适应滑模阻抗控制[J]. 吉林大学学报(工学版), 2016, 46(5): 1602-1608. |
| [10] | 黄晶莹, 秦大同, 刘永刚. 基于自适应滤波的电动汽车电-液复合制动系统防抱死控制[J]. 吉林大学学报(工学版), 2016, 46(4): 1044-1051. |
| [11] | 王春阳, 蔡年春, 李明秋, 刘雪莲. 基于向量的鲁棒分数阶比例微分控制器参数求解算法[J]. 吉林大学学报(工学版), 2015, 45(6): 1933-1940. |
| [12] | 郑宏宇,王琳琳,赵伟强,陈宇超. 基于电控制动系统的客车制动力分配控制策略[J]. 吉林大学学报(工学版), 2015, 45(2): 347-351. |
| [13] | 黄家才, 施昕昕, 李宏胜, 徐庆宏, 石要武. 永磁同步电机调速系统的分数阶积分滑模控制[J]. 吉林大学学报(工学版), 2014, 44(6): 1736-1742. |
| [14] | 吴爱国, 杨硕, 张涵, 李长滨. 压机的调平和跟踪控制[J]. 吉林大学学报(工学版), 2014, 44(4): 1051-1056. |
| [15] | 王帅夫,刘景林. 基于大脑情感学习模型的步进电机控制系统[J]. 吉林大学学报(工学版), 2014, 44(3): 765-770. |
|
||