含切口复合材料应力场和疲劳评估方法

doi:10.13229/j.cnki.jdxbgxb.20230859

吉林大学学报(工学版) ›› 2025, Vol. 55 ›› Issue (5): 1559-1566.doi: 10.13229/j.cnki.jdxbgxb.20230859

含切口复合材料应力场和疲劳评估方法

谌伟^1,²(),边自力^1,²,陈昱文³,邱屿^1,²,徐双喜^1,²,吴轶钢¹()

^1.高性能船舶技术教育部重点实验室（武汉理工大学），武汉 430063
^2.武汉理工大学船海与能源动力工程学院，武汉 430063
^3.中交广航局疏浚公司，广州 510290

收稿日期:2023-08-14 出版日期:2025-05-01 发布日期:2025-07-18
通讯作者: 吴轶钢 E-mail:shenwei_abc@163.com;ewyg@whut.edu.cn
作者简介:谌伟（1986-），男，副教授，博士.研究方向：疲劳、损伤与断裂.E-mail：shenwei_abc@163.com
基金资助:
国家自然科学基金项目(51979209)

Stress field and fatigue assessment method of composite materials with notches

Wei SHEN^1,²(),Zi-li BIAN^1,²,Yu-wen CHEN³,Yu QIU^1,²,Shuang-xi XU^1,²,Yi-gang WU¹()

^1.Key Laboratory of High Performance Ship Technology （Wuhan University of Technology），Ministry of Education，Wuhan 430063，China
^2.School of Naval Architecture，Ocean and Energy Power Engineering，Wuhan University of Technology，Wuhan 430063，China
^3.CCCC Guanghang Dredging Co. ，Ltd. ，Guangzhou 510290，China

Received:2023-08-14 Online:2025-05-01 Published:2025-07-18
Contact: Yi-gang WU E-mail:shenwei_abc@163.com;ewyg@whut.edu.cn

摘要/Abstract

摘要：

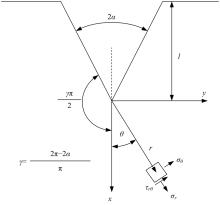
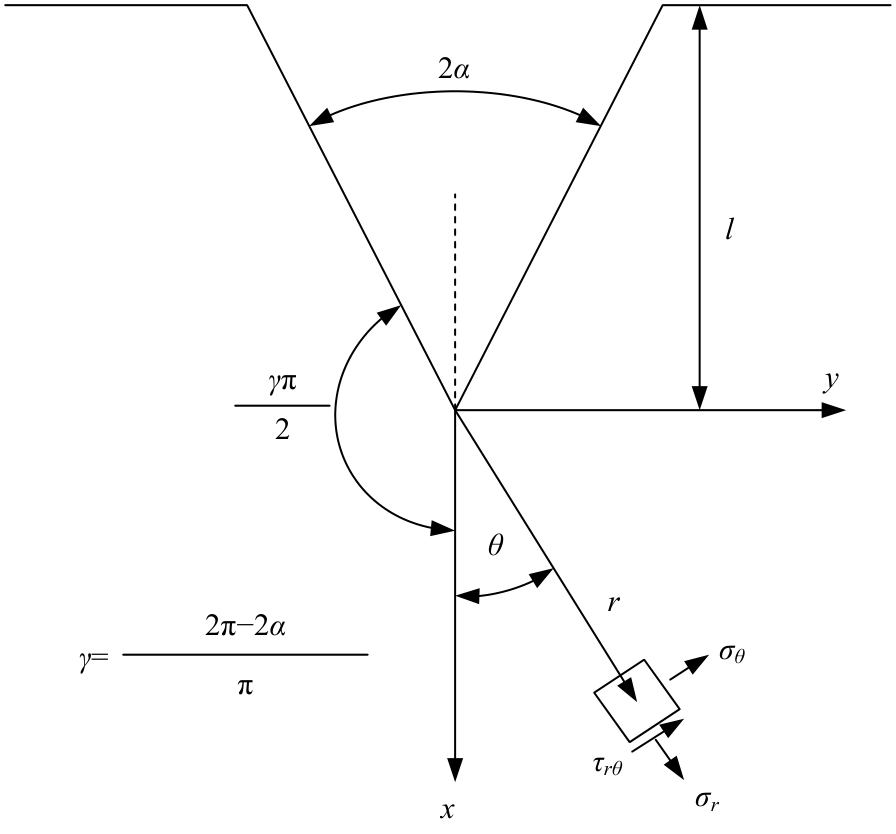
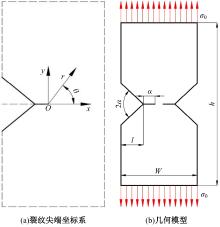
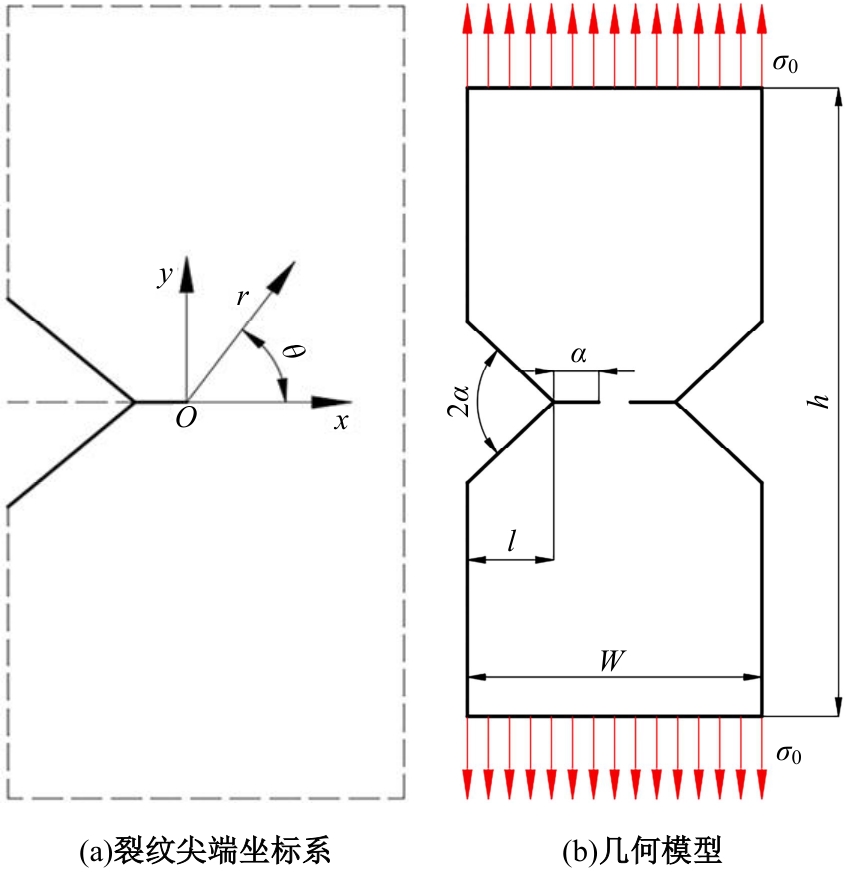
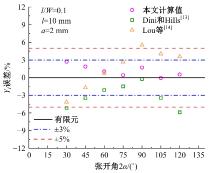
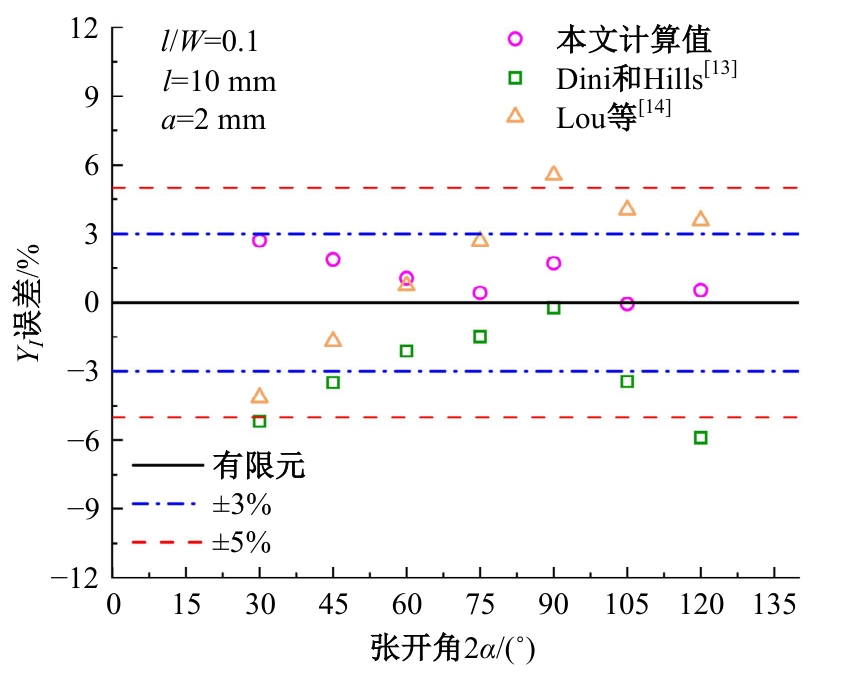
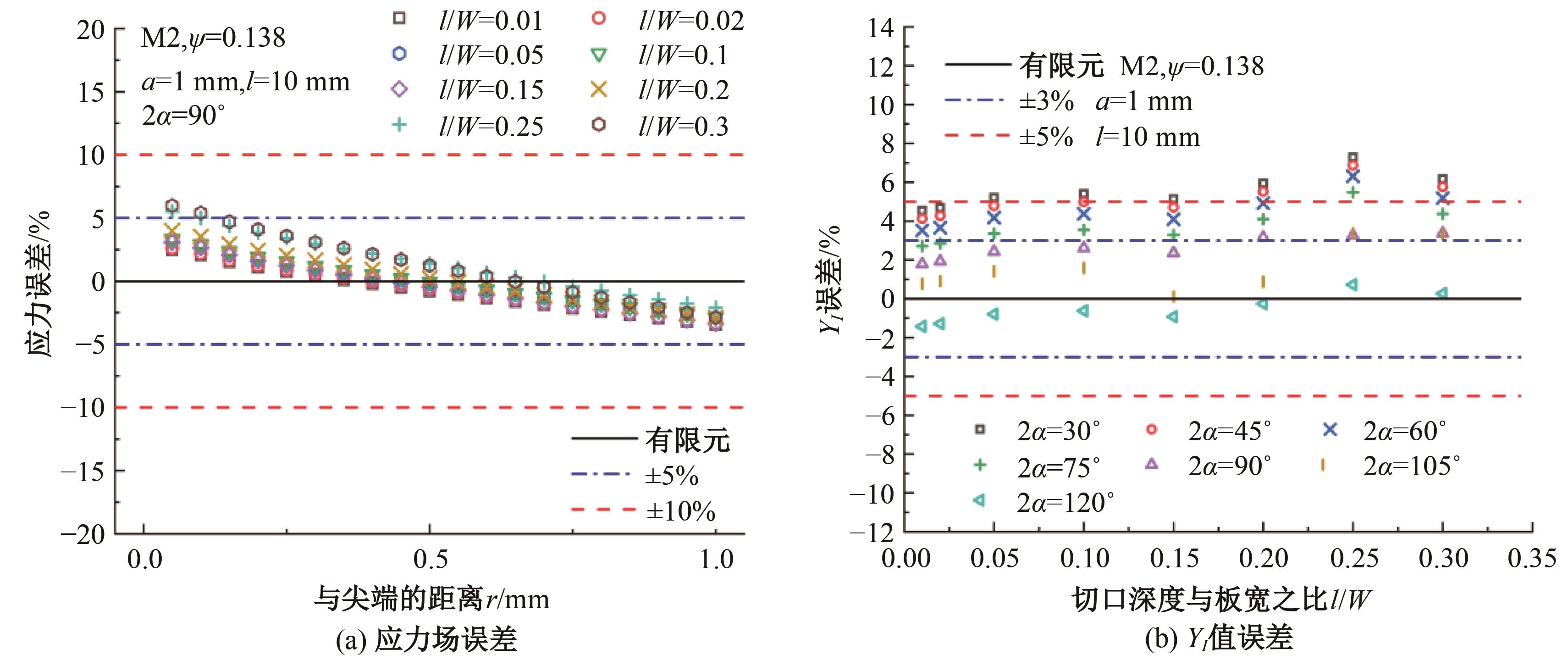
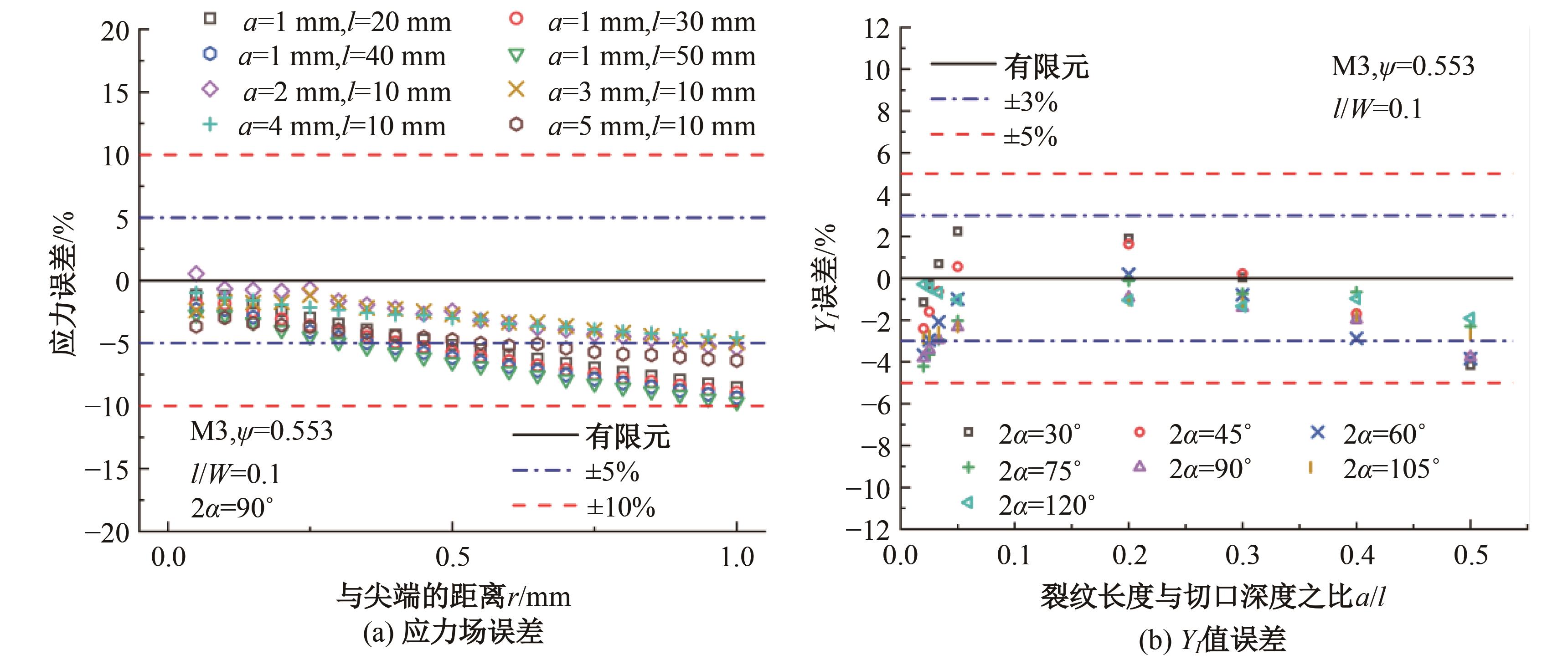
针对含初始裂纹各向异性材料应力场解析公式过于复杂，评估精度受多种几何参数和材料参数影响，不利于工程运用的问题，本文基于传统各向异性材料裂纹尖端附近处的应力场理论公式，建立了含初始裂纹的双边V型切口模型，量化了切口深度、裂纹长度、张开角、材料特性等因素对切口应力场的影响，推导了求解含初始裂纹的双边V型切口构件应力强度因子SIF的简易公式，可用于含裂纹切口构件的应力场和SIF快速预报。对比结果表明：本文简易公式与理论方法和有限元仿真结果误差较小，验证了改进公式的有效性和准确性。

关键词: 复合材料, 各向异性板, 初始裂纹, 切口应力场, 应力强度因子（SIF）

Abstract:

Based on the stress field formula near the crack tip，double-sided V-notch component models with initial cracks were established．The effects of notch depth，crack length，opening angle，material parameters and other factors on the notch stress field were quantified．A simple formula for solving the stress intensity factor SIF of the double-sided V-notch component with initial cracks was derived，which could be used for rapid prediction of the stress field and SIF of the notched component with cracks．The comparison results show that the error between the simplified formula and the theoretical method and finite element simulation results is relatively small， which verifies the effectiveness and accuracy of the improved formula．

Key words: composite, anisotropic plate, initial crack, notch stress field, stress intensity factor

中图分类号:

TB332

谌伟,边自力,陈昱文,邱屿,徐双喜,吴轶钢. 含切口复合材料应力场和疲劳评估方法[J]. 吉林大学学报(工学版), 2025, 55(5): 1559-1566.

Wei SHEN,Zi-li BIAN,Yu-wen CHEN,Yu QIU,Shuang-xi XU,Yi-gang WU. Stress field and fatigue assessment method of composite materials with notches[J]. Journal of Jilin University(Engineering and Technology Edition), 2025, 55(5): 1559-1566.

图/表 15

图1

图2

表1

材料的力学性能"

材料

编号

E_x /GPa

E_y /GPa

ν_xy

ψ

［90］ _n UD碳/

环氧树脂

190.0

9.9

0.35

0.592

［0］ _n 编织玻璃/

环氧树脂

29.7

0.17

0.138

环氧树脂

114.8

11.7

0.21

0.553

表1

表2

数值模型的主要尺寸范围"

尺寸

切口

深度l

裂纹

长度a

切口深度与

板宽之比l/W

长宽比

h/W

张开

角 $2 α$

范围

10~50 mm

1~5 mm

0.01~0.3

30°~120°

表2

图3

图4

图5

图6

图7

图8

图9

图10

图11

图12

图13

参考文献 14

[1]	Li Y F, Sun T, Tian Y S, et al. A stress intensity factor estimation method for the kinked crack under anti-planet load[J]. Theoretical and Applied Fracture Mechanics, 2018, 93: 319-325.
[2]	葛仁余, 牛忠荣, 程长征,等. 反平面V形切口塑性应力奇异性分析[J]. 固体力学学报, 2015, 36(1): 76-84.
	Ge Ren-yu, Niu Zhong-rong, Cheng Chang-zheng, et al. Analysis of plastic stress singularities of anti-plane V-notches in hardening materials[J]. Chinese Journal of Solid Mechanics, 2015, 36(1): 76-84.
[3]	Shipman, Benjamin H. Calculation of the generalized stress intensity factors for a V-notched anisotropic body[D]. Raleigh: North Carolina State University, 2002.
[4]	Yao S L, Zappalorto M, Pan W, et al. Two dimensional displacement and stress fields for tri-material V-notches and sharp inclusions in anisotropic plates[J]. European Journal of Mechanics A: Solids, 2020, 80: 103927.
[5]	Yu Y F, Pei X J, Wang P, et al. A structural stress approach accounting for notch effects on fatigue propagation life: part I theory[J]. International Journal of Fatigue, 2022, 159: 106793.
[6]	孙齐. 预置裂纹复合材料层合板拉伸性能及裂纹扩展分析[D]. 大连: 大连理工大学汽车工程学院, 2020.
	Sun Qi. Analysis of tensile properties and crack propagation of pre-cracked composite laminates[D]. Dalian: College of Automotive Engineering, Dalian University of Technology, 2020.
[7]	李碧琛. CF/EP复合材料裂纹扩展的数值模拟与试验研究[D]. 哈尔滨: 哈尔滨工业大学材料科学与工程学院, 2014.
	Li Bi-chen. Numerical simulation and experimental research on crack propagation in CF/EP composite materials[D]. Harbin: College of Materials Science and Engineering, Harbin Institute of Technology, 2014.
[8]	罗白璐, 朱英富, 李之达,等. 夹芯结构的疲劳裂纹损伤扩展研究[J]. 船舶力学, 2019, 23(8): 988-996.
	Luo Bai-lu, Zhu Ying-fu, Li Zhi-da, et al. Research on fatigue crack damage propagation of sandwich structures[J]. Journal of Ship Mechanics, 2019, 23(8): 988-996.
[9]	Williams M L. Stress singularities resulting from various boundary conditions in angular corners of plate in extension[J]. Journal of Applied Mechanics-Transactions of the Asme, 1952, 19(4): 526-528.
[10]	Zappalorto M, Carraro P A. Stress fields at sharp angular corners in thick anisotropic composite plates[J]. Composite Structures, 2014, 117(1): 346-353.
[11]	Zappalorto M. Mode I generalised stress intensity factors for rounded notches in orthotropic plates[J]. Theoretical and Applied Fracture Mechanics, 2019, 101: 356-364.
[12]	Zappalorto M, Ricotta M. Effect of material orthotropy on the notch stress intensity factors of sharp V-notched plates under tension[J]. Theoretical & Applied Fracture Mechanics, 2019, 104: 102375.
[13]	Dini D, Hills D A. When does a notch behave like a crack[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2006, 220(1): 27-43.
[14]	Lou B Q, Barltrop N. Physical differences between models of an infinitesimal crack at a V-notch edge and a crack emanating from a V-notch tip along with their approximate solutions[J]. International Journal of Solids & Structures, 2021, 219: 1-10.

相关文章 15

[1]	姜浩,赵正文. 玄武岩纤维网格水泥基复合材料加固RC梁抗剪性能试验[J]. 吉林大学学报(工学版), 2025, 55(1): 211-220.
[2]	娄淑梅,李一明,李鑫,陈鹏,白雪峰,程宝嘉. 基于BP神经网络和Arrhenius本构模型的石墨烯/7075复合材料热变形行为[J]. 吉林大学学报(工学版), 2024, 54(5): 1237-1245.
[3]	刘晓波,杨淼,周德坤. （Mg₂Si+Si）/Al复合材料的组织和耐磨性[J]. 吉林大学学报(工学版), 2024, 54(4): 938-946.
[4]	杨超,姚青云,唐双美,陈其龙,覃峰. 氟化石墨烯/聚酰亚胺复合膜的导热和电绝缘性能[J]. 吉林大学学报(工学版), 2024, 54(3): 663-673.
[5]	许良,肖景厚,宋万万,周松. 碳纤维复合材料层合板三点弯曲疲劳性能[J]. 吉林大学学报(工学版), 2024, 54(2): 400-409.
[6]	于本田,李彦宵,张占旭,苏俊辉,谢超,张凯. 不同石粉及掺量对高延性工程水泥基复合材料的性能影响[J]. 吉林大学学报(工学版), 2024, 54(10): 2908-2921.
[7]	郑植,袁佩,金轩慧,魏思斯,耿波. 桥墩复合材料柔性防撞护舷试验[J]. 吉林大学学报(工学版), 2023, 53(9): 2581-2590.
[8]	车佳玲,王俊,刘海峰,张居平. 沙漠砂制备高韧性水泥基复合材料在不同环境下的自愈合性能[J]. 吉林大学学报(工学版), 2023, 53(8): 2277-2286.
[9]	许良,边钰博,周松,肖景厚. 高温水浸对T800/环氧树脂基复合材料性能的影响[J]. 吉林大学学报(工学版), 2023, 53(7): 1943-1950.
[10]	魏海斌,韩栓业,毕海鹏,刘琼辉,马子鹏. 智能感知道路主动除冰雪系统及实验技术[J]. 吉林大学学报(工学版), 2023, 53(5): 1411-1417.
[11]	魏海斌,马子鹏,毕海鹏,刘汉涛,韩栓业. 基于力学响应分析方法的导电橡胶复合路面铺装技术[J]. 吉林大学学报(工学版), 2023, 53(2): 531-537.
[12]	郑植,耿波,王福敏,董俊宏,魏思斯. 既有低等级混凝土护栏防护能力提升[J]. 吉林大学学报(工学版), 2022, 52(6): 1362-1374.
[13]	李伟,宋海生,陆浩宇,史文库,王强,王晓俊. 复合材料板簧迟滞特性线性辨识方法[J]. 吉林大学学报(工学版), 2022, 52(4): 829-836.
[14]	庄蔚敏,陈沈,吴迪. 碳纤维增强复合材料包裹强化形式对钢管横向冲击性能的影响[J]. 吉林大学学报(工学版), 2022, 52(4): 819-828.
[15]	于开锋,何小玲,李俊涛,梁策. 玄武岩纤维对不饱和聚酯树脂复合材料的增韧[J]. 吉林大学学报(工学版), 2022, 52(10): 2300-2306.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

含切口复合材料应力场和疲劳评估方法

Stress field and fatigue assessment method of composite materials with notches

RICH HTML

PDF (PC)

摘要/Abstract

引用本文

使用本文

图/表 15

参考文献 14

相关文章 15

Metrics

本文评价

推荐阅读 10