基于参数相关性分析和机器学习算法的高强混凝土徐变预测

doi:10.13229/j.cnki.jdxbgxb.20230814

摘要/Abstract

摘要：

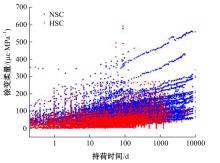
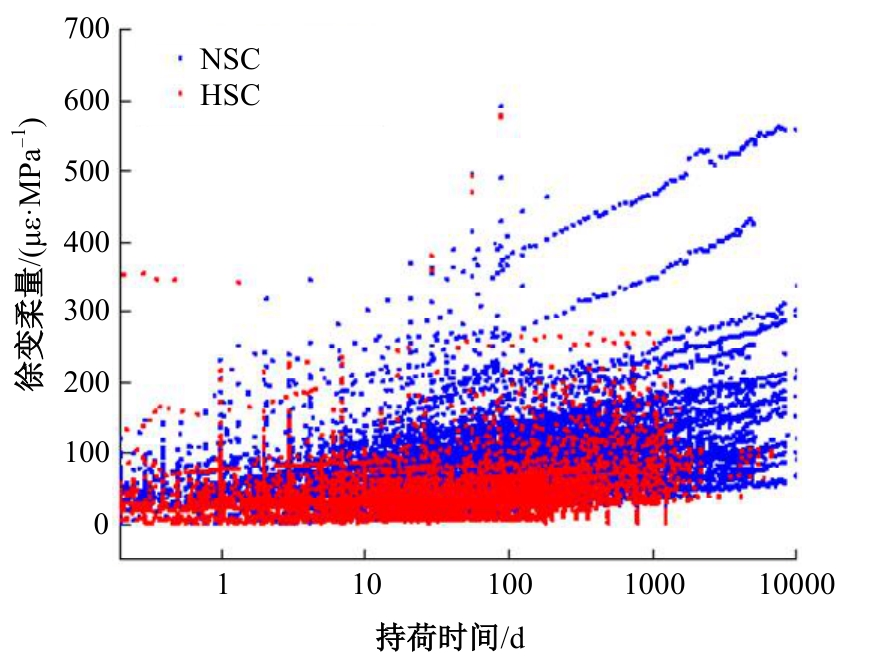
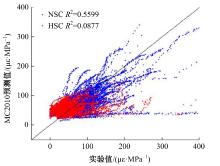
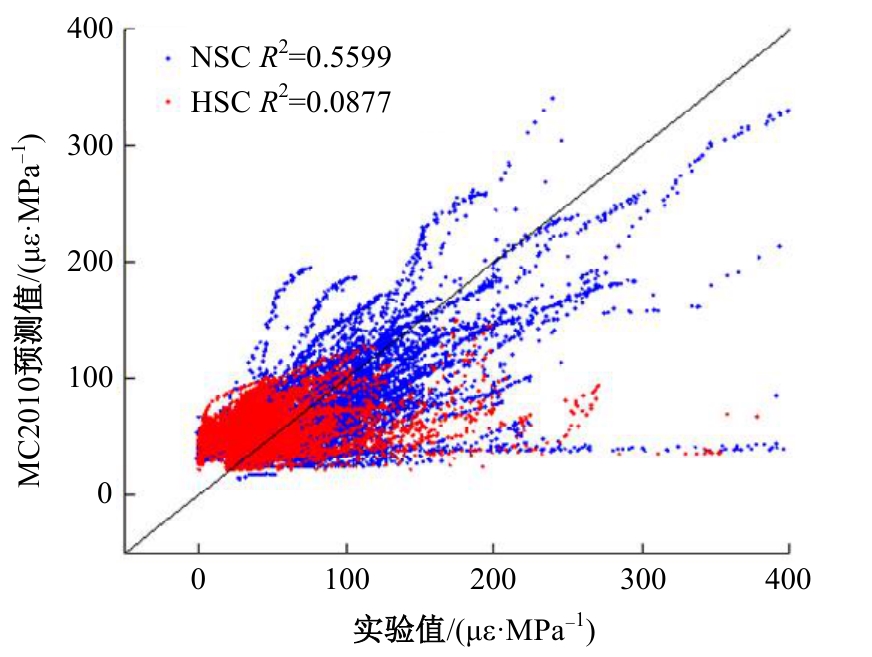
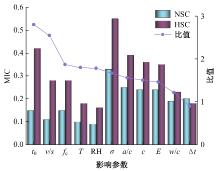
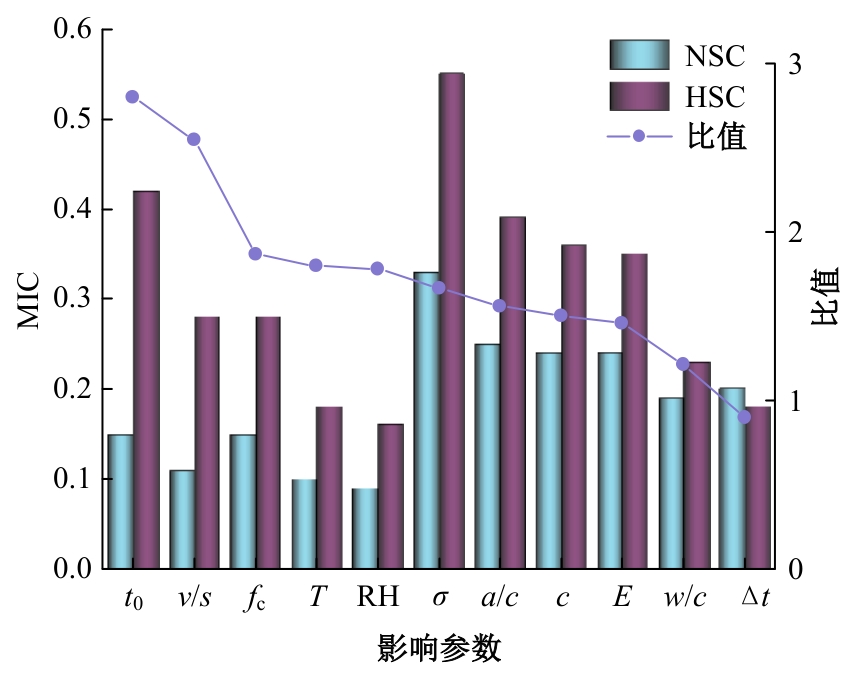
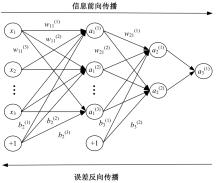
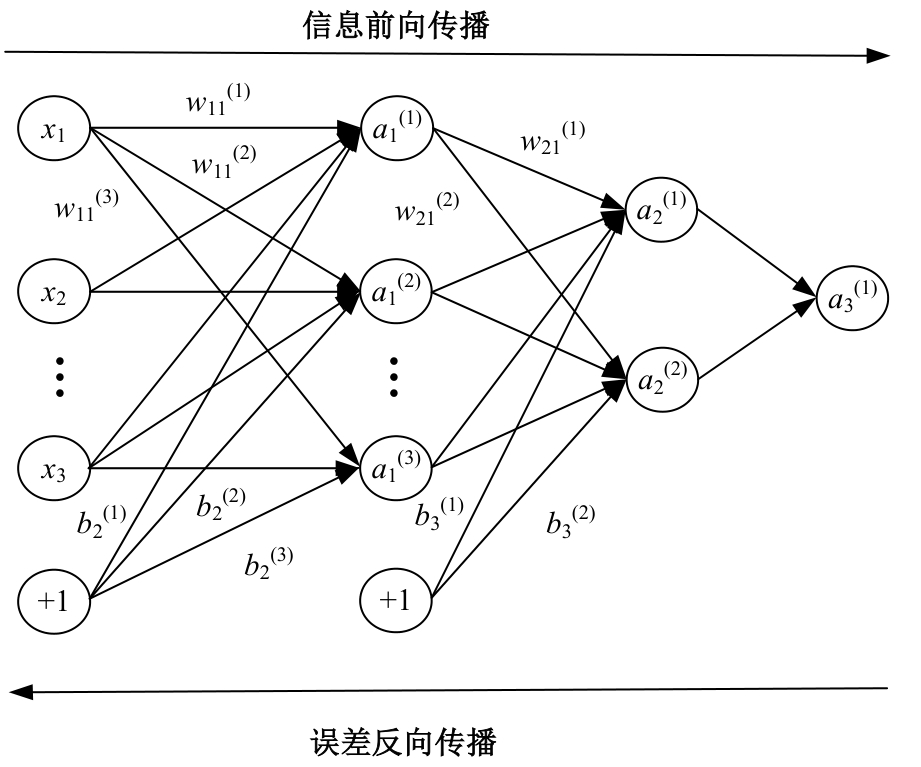
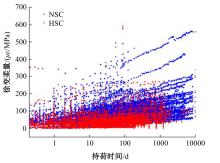
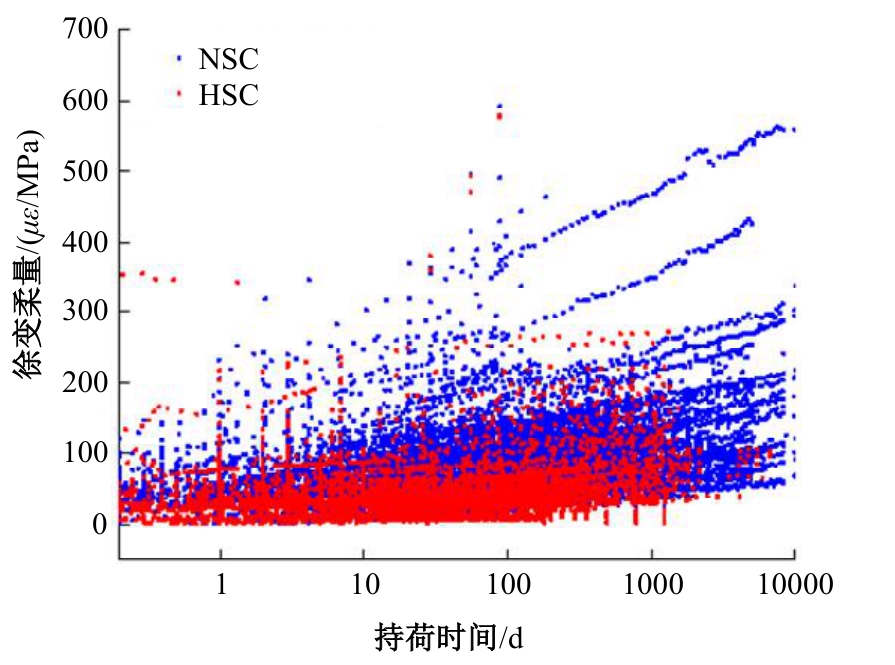
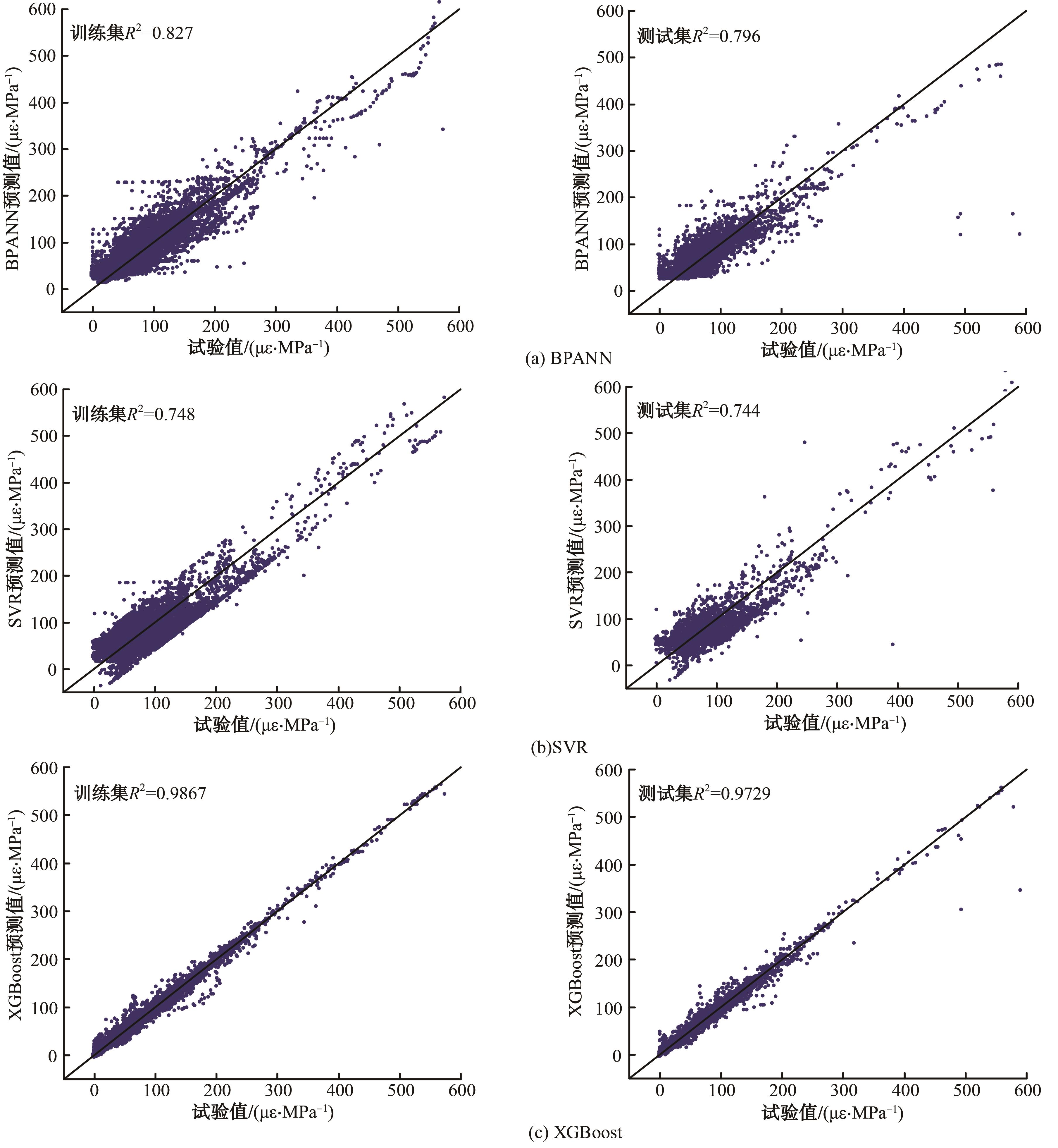
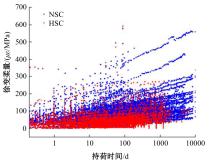
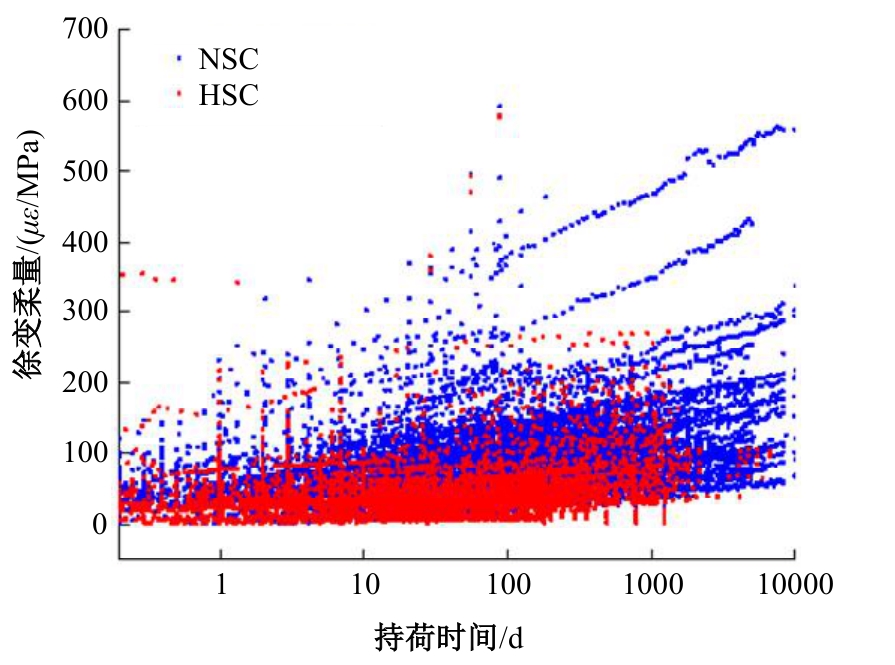
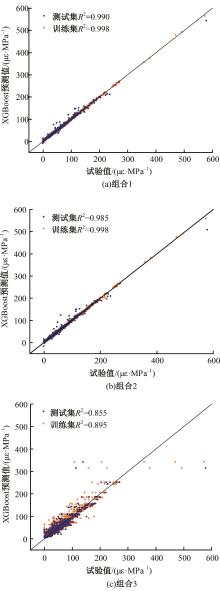
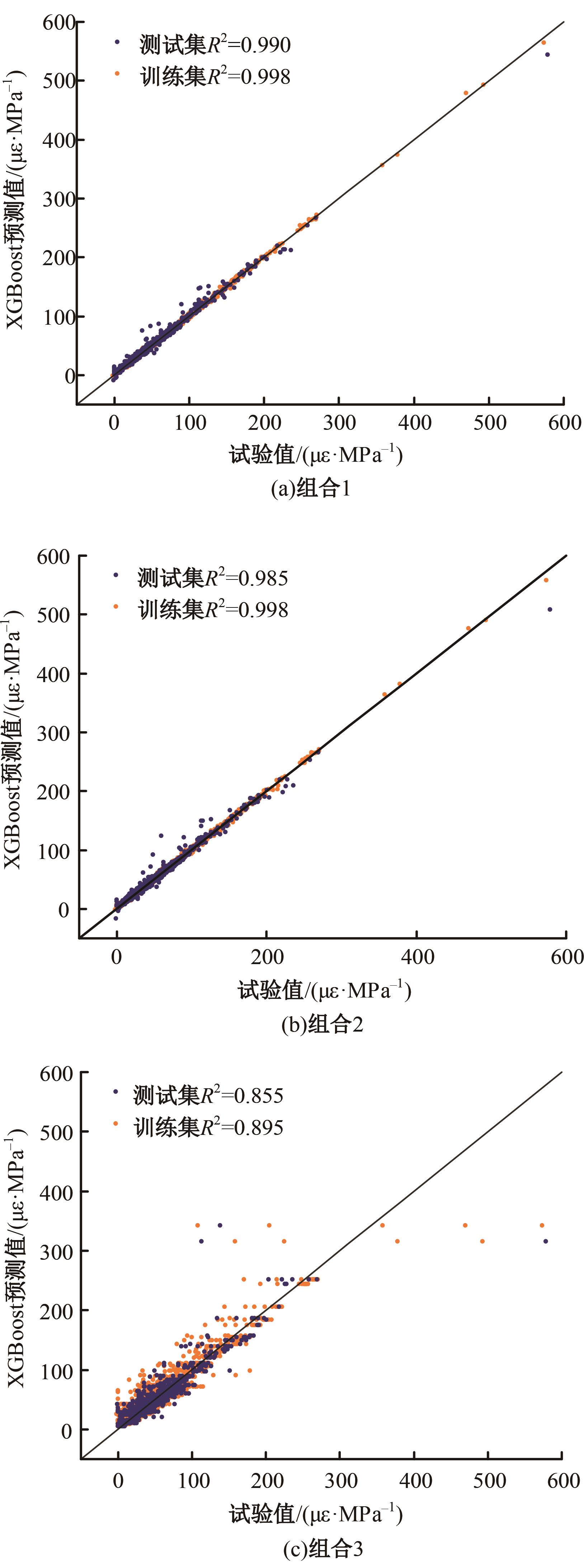
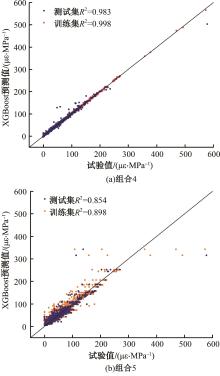
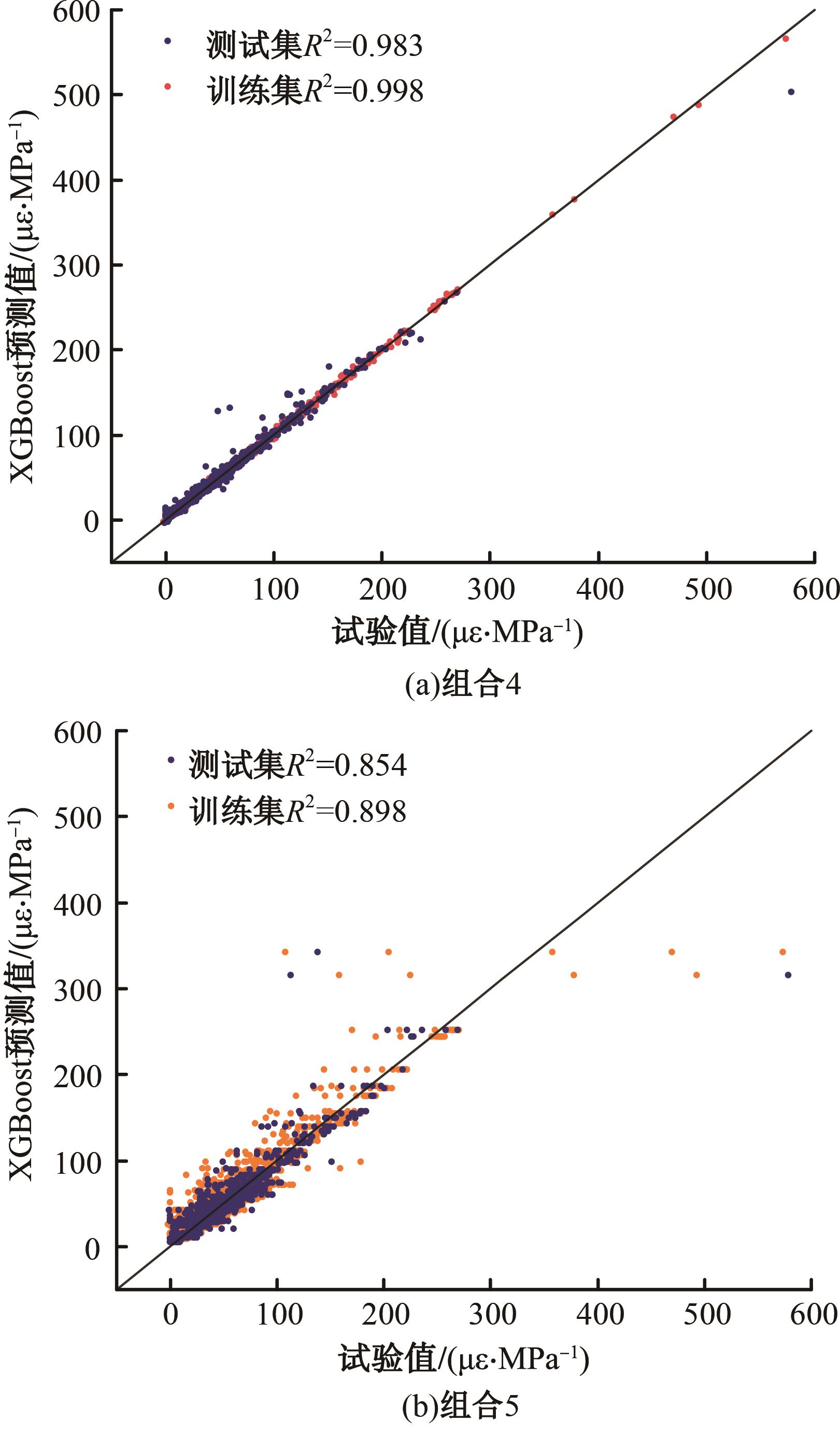
针对预测混凝土徐变的机器学习模型已有较多研究，但区分混凝土强度的研究较少的问题，基于NU-ITI数据库，采用3种机器学习模型，即反向传播人工神经网络、支持向量回归和极端梯度提升（XGBoost）建立了混凝土徐变的预测模型。结果表明，XGBoost能很好地预测混凝土的徐变（R²=0.972 9）。通过对高强混凝土参数的相关性分析，筛选出相关系数最高和最低的参数组。基于参数筛选后的XGBoost模型重新对高强混凝土徐变进行计算，发现筛除弱相关参数会显著降低计算结果的鲁棒性。本文研究表明，高强混凝土徐变影响参数之间存在不同程度的相关性，筛除强相关参数对模型计算准确性影响较小，而筛除弱相关参数影响较大。研究成果可为高强混凝土徐变的建模提供参考。

关键词: 结构工程, 高强混凝土徐变, 机器学习模型, 最大信息相关系数, 鲁棒性

Abstract:

Although machine learning models for predicting concrete creep have been numerous studied， but only a few studies have distinguished concrete strength. Firstly， based on NU-ITI database， three machine learning models BPANN， SVR and XGBoost are used to build a prediction model for concrete creep. The results indicate that XGBoost can effectively predict the creep of concrete （R²=0.972 9）. Secondly， through the analysis of correlations among parameters of high strength concrete， the parameter groups with the highest and lowest correlation coefficients were identified. Based on the parameter selection， the XGBoost models was recalculated for high strength concrete creep， revealing that excluding weakly correlated parameters significantly reduces the robustness of the computational results. This study demonstrates that there are varying degrees of correlation among parameters affecting the creep of high strength concrete. The exclusion of strongly correlated parameters has a minor impact on the accuracy of the model calculations， while the exclusion of weakly correlated parameters has a more significant effect. The research findings can serve as a reference for modeling the creep of high strength concrete.

Key words: structural engineering, high strength concrete creep, machine learning model, maximum information coefficient， robustness

中图分类号:

TU17

梅生启,刘晓东,王兴举,李旭峰,武腾,程相旭. 基于参数相关性分析和机器学习算法的高强混凝土徐变预测[J]. 吉林大学学报(工学版), 2025, 55(5): 1595-1603.

Sheng-qi MEI,Xiao-dong LIU,Xing-ju WANG,Xu-feng LI,Teng WU,Xiang-xu CHENG. Prediction of high strength concrete creep based on parametric MIC analysis and machine learning algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2025, 55(5): 1595-1603.

图/表 17

图1

图2

表1

图3

图4

表2

图5

表3

表4

图6

图7

表5

表6

图8

表7

图9

表8

参考文献 25

[1]	Vandamme M, Ulm F J. Nanogranular origin of concrete creep[J]. Proceedings of the National Academy of Sciences, 2009, 106(26): 10552-10557.
[2]	黄永辉, 刘爱荣, 傅继阳, 等.高强钢管高强混凝土徐变特性试验研究[J]. 工程力学, 2021,38(8): 204-212.
	Huang Yong-hui, Liu Ai-rong, Fu Ji-yang, et al. Experimental study on the creep characteristics of high-strength concrete filled high-strength steel tube [J]. Engineering Mechanics, 2021, 38(8): 204-212.
[3]	柯敏勇, 刘海祥, 陈松.桥用高强混凝土双轴徐变试验研究[J].建筑结构学报,2012, 33(6): 116-122.
	Ke Min-yong, Liu Hai-xiang, Chen Song. Biaxial creep experiment for high strength concrete in bridge engineering [J]. Journal of Building Structures, 2012, 33(6): 116-122.
[4]	Le Roy R, Le Maou F, Torrenti J M. Long term basic creep behavior of high performance concrete: data and modelling[J]. Materials and Structures, 2017, 50(1): 1-11.
[5]	ACI Committee 209.209R1-92: Prediction of creep, shrinkage and temperature effects in concrete structures. manual of concrete practice part 1 [S/OL]. [1992-01-03].
[6]	Betonbau. Fib model code for concrete structures 2010[J]. Ernst Shon, 2013: 97834336.
[7]	Gardner N J, Lockman M J. Design provisions for drying shrinkage and creep of normal strength concrete [J]. ACI Materials Journal, 2001, 98(2): 159-167.
[8]	Bažant Z P, Baweja S. Creep and shrinkage prediction model for analysis and design of concrete structures: model B3[J]. Materials and Structures, 1995, 28(6): 357-365.
[9]	Bažant Z P, Wendner R. RILEM draft recommendation. TC-242-MDC multi-decade creep and shrinkage of concreteL Material model and structural analysis Model B4 for creep, drying shrinkage and autogenous shrinkage of normal and high-strength concretes with multi-decad applicability[J]. Materials Structures, 2015, 48(4): 753-770.
[10]	Peng Y, Unluer C. Modeling the mechanical properties of recycled aggregate concrete using hybrid machine learning algorithms[J]. Resources, Conservation and Recycling, 2023, 190: 106812.
[11]	Yang Z, Zhu H, Zhang B, et al. Short-term creep behaviors of seawater sea-sand coral aggregate concrete: An experimental study with rheological model and neural network[J]. Construction and Building Materials, 2023, 363: 129786.
[12]	Pham A D, Hoang N D, Nguyen Q T. Predicting compressive strength of high-performance concrete using metaheuristic-optimized least squares support vector regression[J]. Journal of Computing in Civil Engineering, 2016, 30(3): No.06015002.
[13]	Liang M, Chang Z, Wan Z, et al. Interpretable ensemble-machine-learning models for predicting creep behavior of concrete[J]. Cement and Concrete Composites, 2022, 125: 104295.
[14]	曲广雷, 闫宗伟, 郑木莲, 等. 基于神经网络与回归分析的多孔混凝土性能预测[J]. 吉林大学学报:工学版, 2025, 55(1): 269-282.
	Qu Guang-lei, Yan Zong-wei, Zheng Mu-lian, et al. Performance prediction of porous concrete based on neural network and regression analysis[J]. Journal of Jilin University (Engineering and Technology Editon), 2025, 55(1): 269-282.
[15]	Xu J, Zhao X, Yu Y, et al. Parametric sensitivity analysis and modelling of mechanical properties of normal-and high-strength recycled aggregate concrete using grey theory, multiple nonlinear regression and artificial neural networks[J]. Construction and Building Materials, 2019, 211: 479-491.
[16]	Park D, Rilett L R. Forecasting freeway link travel times with a multilayer feedforward neural network[J]. Computer‐Aided Civil and Infrastructure Engineering, 1999, 14(5): 357-367.
[17]	Reshef D N, Reshef Y A, Finucane H K, et al. Detecting novel associations in large data sets[J]. Science, 2011, 334(6062): 1518-1524.
[18]	Li K, Long Y, Wang H, et al. Modeling and sensitivity analysis of concrete creep with machine learning methods[J]. Journal of Materials in Civil Engineering, 2021, 33(8): 04021206.
[19]	Hubler M H, Wendner R, Bazant Z P. Comprehensive database for concrete creep and shrinkage: Analysis and recommendations for testing and recording[J]. ACI Materials Journal, 2015, 112(4): 547-558.
[20]	Tang L, Na S H. Comparison of machine learning methods for ground settlement prediction with different tunneling datasets[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2021, 13(6): 1274-1289.
[21]	Hastie T, Tibshirani R, Friedman J H, et al. The Elements of Statistical Learning: Data Mining, Inference, and Prediction[M]. New York: Springer, 2009.
[22]	Cortes C, Vapnik V. Support-vector networks[J]. Machine Learning, 1995, 20: 273-297.
[23]	Pedregosa F, Varoquaux G, Gramfort A, et al. Scikit-learn: machine learning in python[J]. Journal of Machine Learning Research, 2011, 12: 2825-2830.
[24]	Chen T, Guestrin C. XGBoost: a scalable tree boosting system[C]∥Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, USA, 2016: 785-794.
[25]	Zeghal M. Modeling the creep compliance of asphalt concrete using the artificial neural network technique[C]∥GeoCongress 2008: Characterization, Monitoring, and Modeling of GeoSystems, New Orleans, USA, 2008: 910-916.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

模型	类型	影响参数
B4	内部影响参数	骨料重量、含气量、水泥含量、水泥种类、弹性模量、水灰比、抗压强度
B4	外部影响参数	环境相对湿度、环境温度、干燥龄期
MC2010	内部影响参数	水泥类型、抗压强度、弹性模量
MC2010	外部影响参数	加载龄期、截面尺寸、环境相对湿度、环境温度、应力等级、持荷时间

性能指标	BPANN		SVR		XGBoost
性能指标	训练集	测试集	训练集	测试集	训练集	测试集
OBJ	24.41		32.90		5.80
RMSE/10^-6（με·MPa^－1）	23.51	23.60	28.36	29.11	6.50	9.46
MAE/10^-6（με·MPa^－1）	16.59	16.40	22.81	22.73	4.06	5.28
R²	0.827 0	0.796 0	0.748 0	0.744 0	0.986 7	0.972 9

组合	类型	参数
1	HSC	v/s、t₀、σ、f_c、RH、E、T、a/c、c、w/c、Δt
2	HSC	v/s、t₀、σ、f_c、RH、E、T、w/c、Δt
3	HSC	v/s、t₀、σ、RH、E、T、a/c、c、w/c

性能指标	组合1		组合2		组合3
性能指标	训练集	测试集	训练集	测试集	训练集	测试集
OBJ	1.54		1.73		10.90
RMSE/（με·MPa^－1）	1.30×10^-6	3.57×10^-6	1.45×10^-6	4.38×10^-6	11.97×10^-6	13.77×10^-6
MAE/（με·MPa^－1）	0.97×10^-6	1.85×10^-6	1.00×10^-6	2.00×10^-6	6.97×10^-6	7.17×10^-6
R²	0.998	0.990	0.998	0.985	0.895	0.855

性能指标	组合4		组合5
性能指标	训练集	测试集	训练集	测试集
OBJ	1.78		10.89
RMSE/（με·MPa^－1）	1.46× 10^-6	4.68× 10^-6	11.96× 10^-6	13.77× 10^-6
MAE/（με·MPa^－1）	1.02× 10^-6	2.04× 10^-6	6.99× 10^-6	7.17× 10^-6
R²	0.998	0.983	0.898	0.854