多车桥梁动态称重算法

doi:10.13229/j.cnki.jdxbgxb20200018

吉林大学学报(工学版) ›› 2021, Vol. 51 ›› Issue (2): 583-596.doi: 10.13229/j.cnki.jdxbgxb20200018

• 交通运输工程·土木工程 • 上一篇

多车桥梁动态称重算法

宫亚峰¹(),宋加祥¹,谭国金¹(),毕海鹏¹,刘洋^2,^3,⁴,单承新⁵

^1.吉林大学交通学院，长春 130022
^2.中交第二航务工程局有限公司，武汉 430040
^3.长大桥梁建设施工技术交通行业重点实验室，武汉 431400
^4.交通运输行业交通基础设施智能制造研发中心，武汉 431400
^5.长春空港翔悦投资有限公司，长春 130000

收稿日期:2020-01-07 出版日期:2021-03-01 发布日期:2021-02-09
通讯作者: 谭国金 E-mail:gongyf@jlu.edu.cn;tgj@jlu.edu.cn
作者简介:宫亚峰（1977-），男，教授，博士.研究方向：桥梁结构健康监测理论及应用.E-mail:gongyf@jlu.edu.cn
基金资助:
国家自然科学基金项目(51978309);吉林省科技发展计划项目(20200403157SF);吉林省教育厅“十三五”科学技术项目(JJKH20190150KJ);吉林省交通运输科技项目(2018ZDGC-16);吉林省发展改革委产业技术研究与开发项目(2019C041-5);中央高校基本科研业务费专项资金项目

Multi⁃vehicle bridge weigh⁃in⁃motion algorithm

Ya-feng GONG¹(),Jia-xiang SONG¹,Guo-jin TAN¹(),Hai-peng BI¹,Yang LIU^2,^3,⁴,Cheng-xin SHAN⁵

^1.College of Transportation，Jilin University，Changchun 130022，China
^2.China Communications Second Navigation Engineering Bureau Co. ，Ltd. ，Wuhan 430040，China
^3.Changda Bridge Construction Technology Transportation Industry Key Laboratory，Wuhan 431400，China
^4.Transportation Infrastructure Intelligent Manufacturing R&D Center for Transportation Infrastructure，Wuhan 431400，China
^5.Changchun Airport Xiangyue Investment Co. ，Ltd. ，Changchun 130000，China

Received:2020-01-07 Online:2021-03-01 Published:2021-02-09
Contact: Guo-jin TAN E-mail:gongyf@jlu.edu.cn;tgj@jlu.edu.cn

摘要/Abstract

摘要：

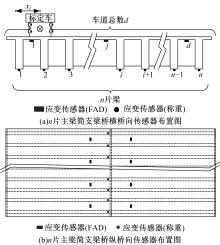
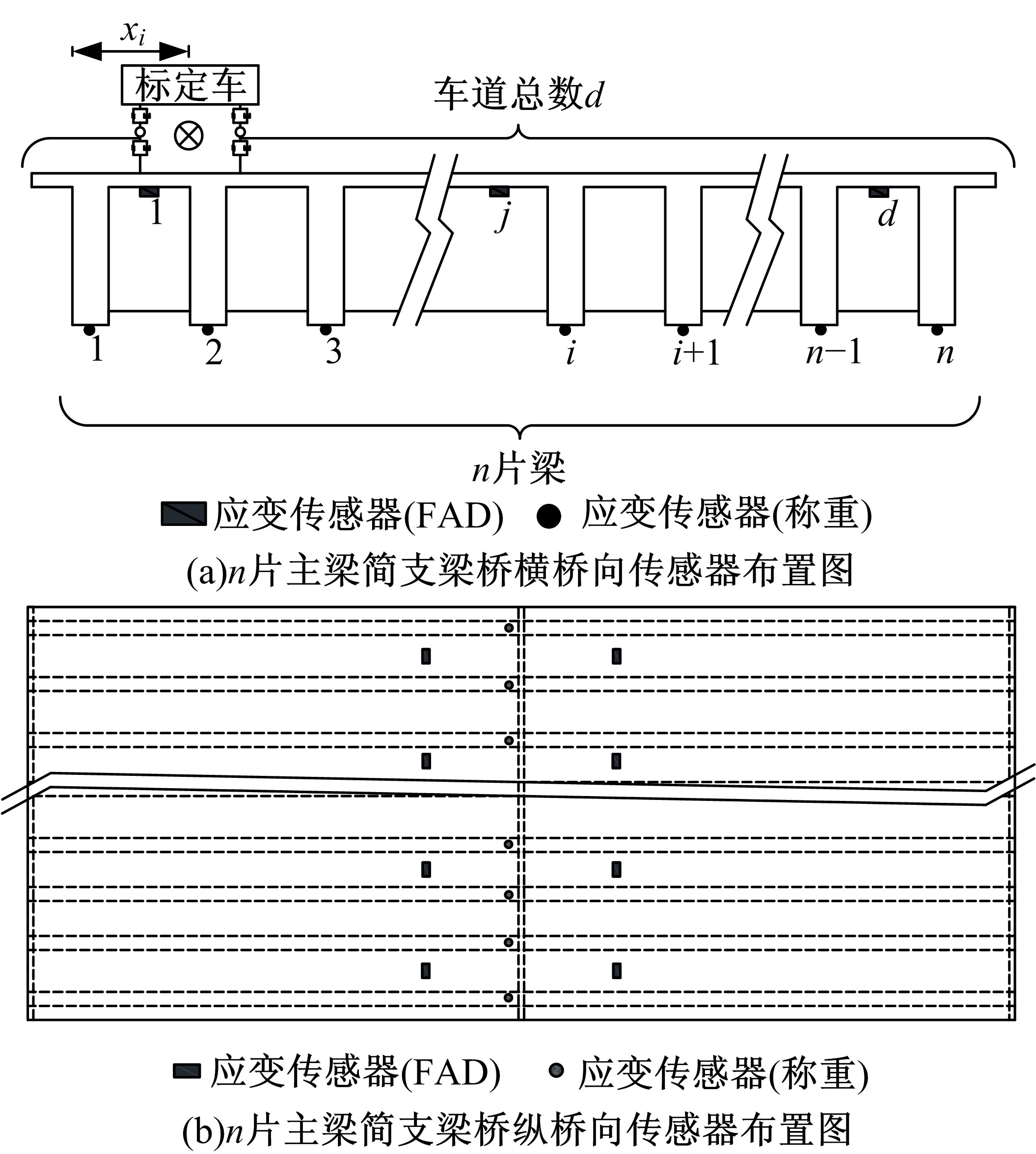
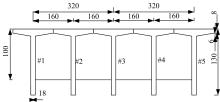
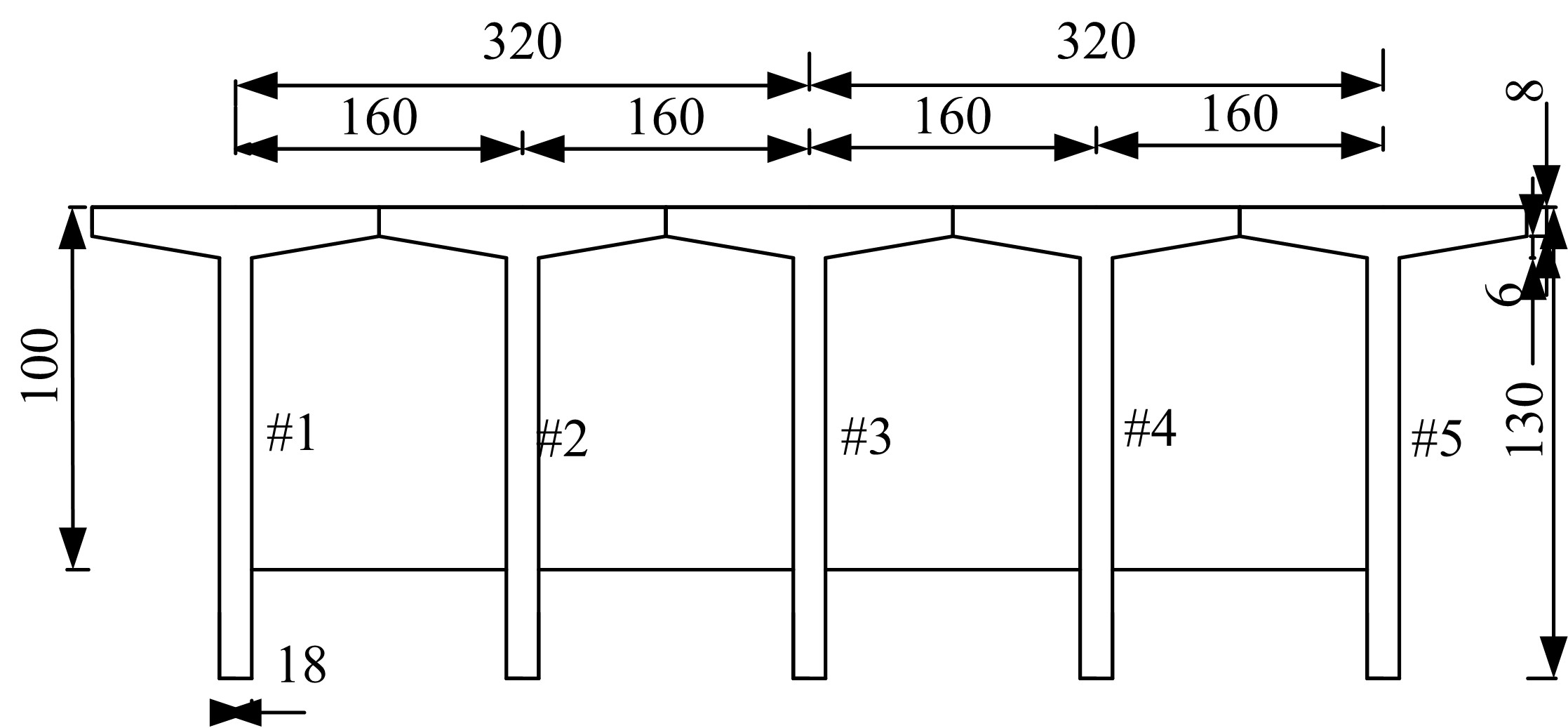
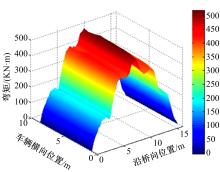
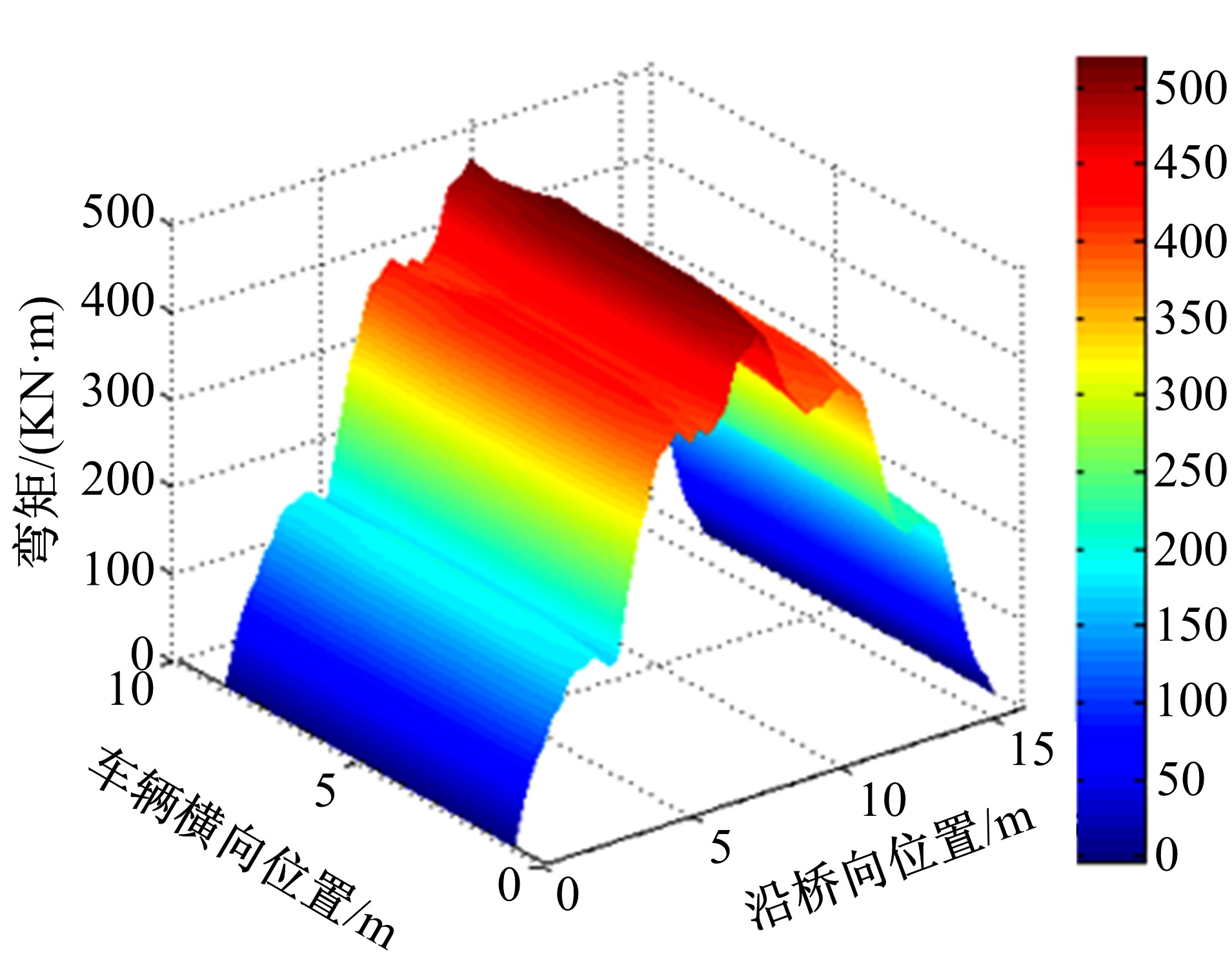
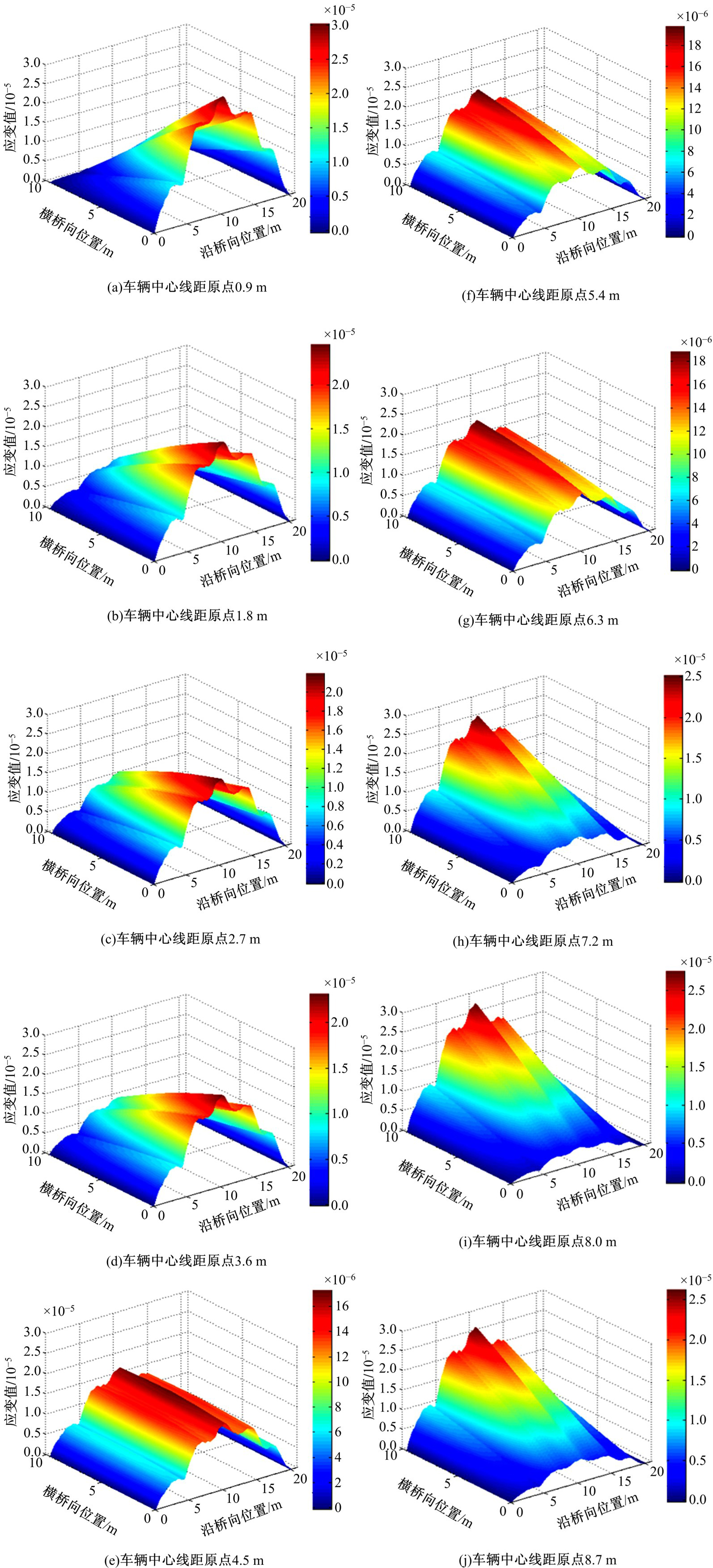
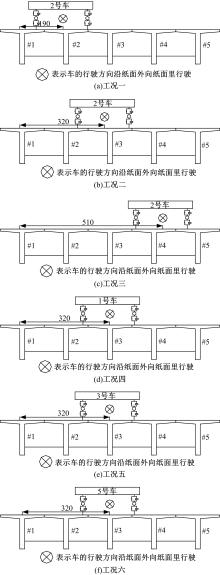
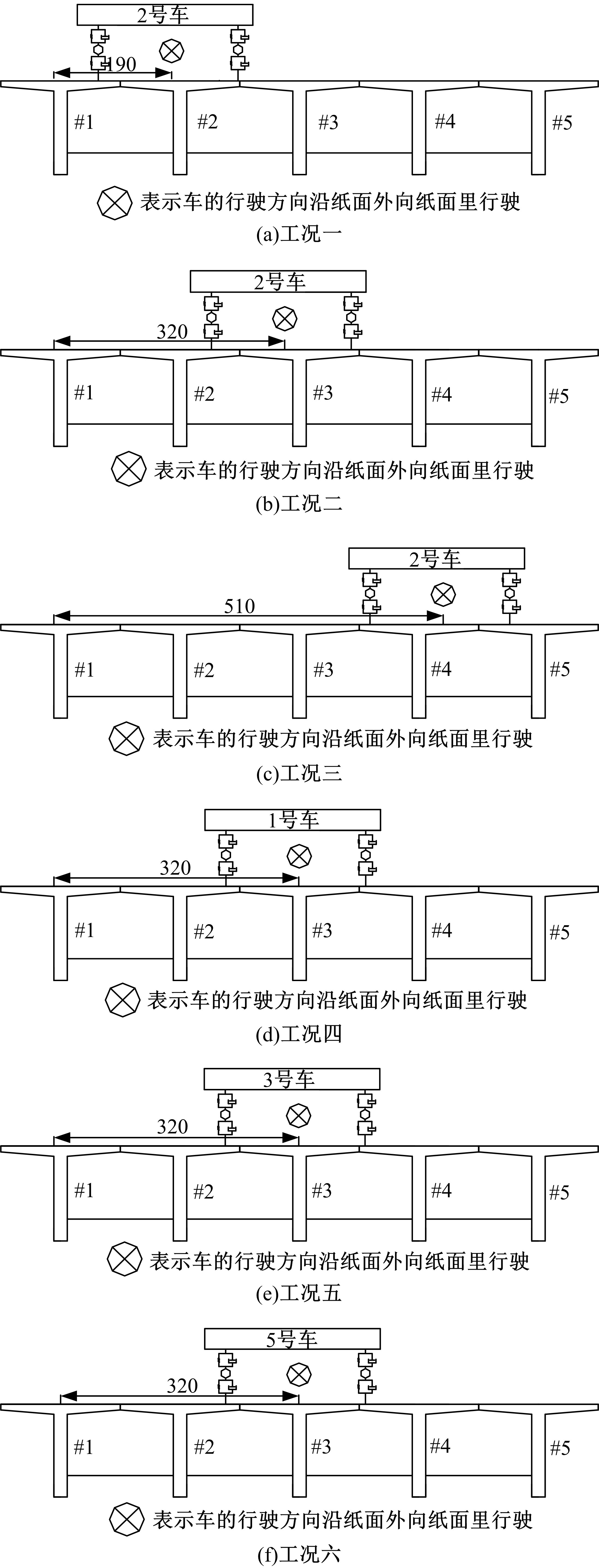
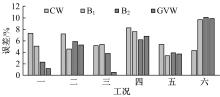
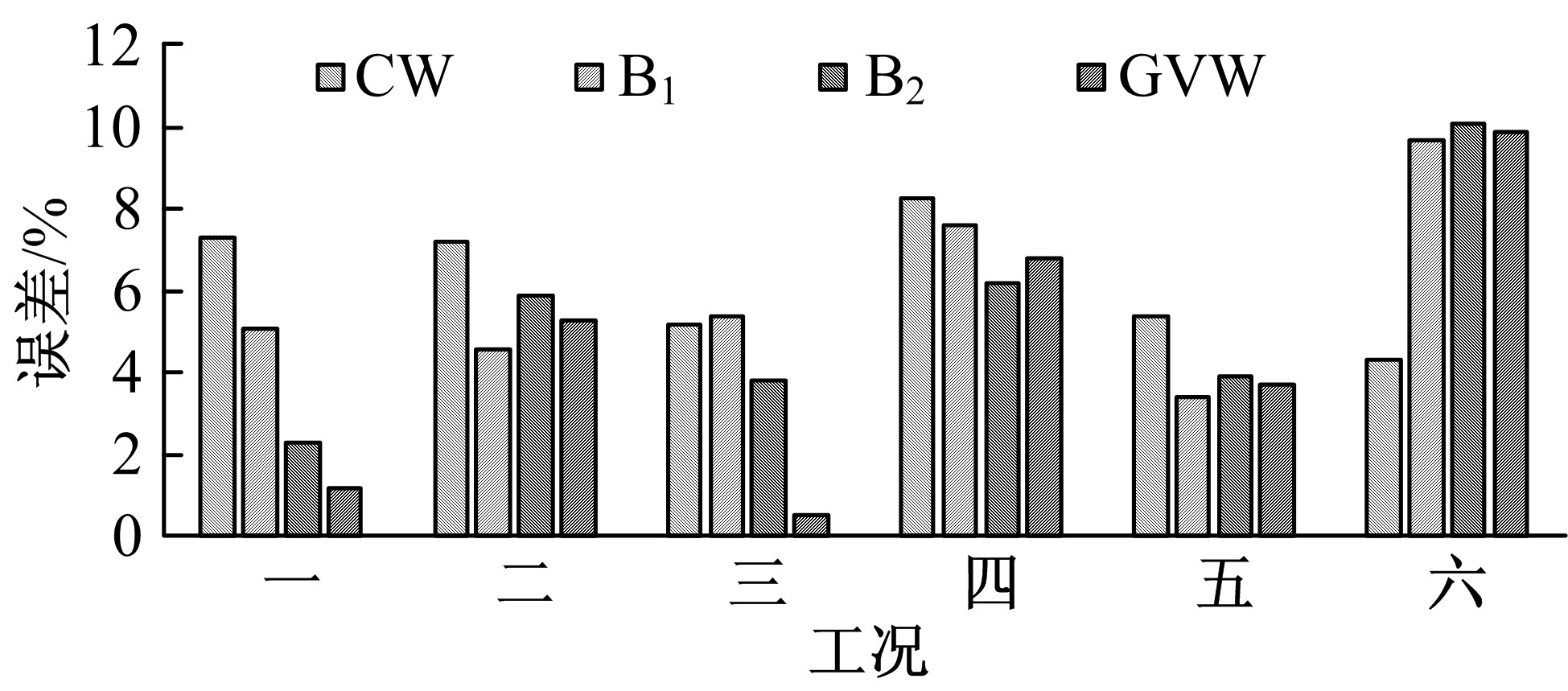
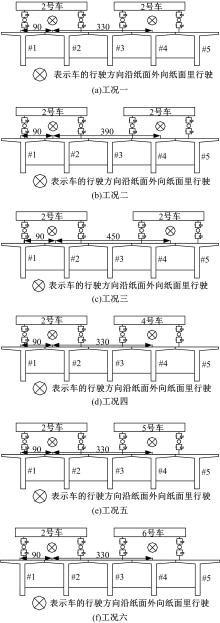
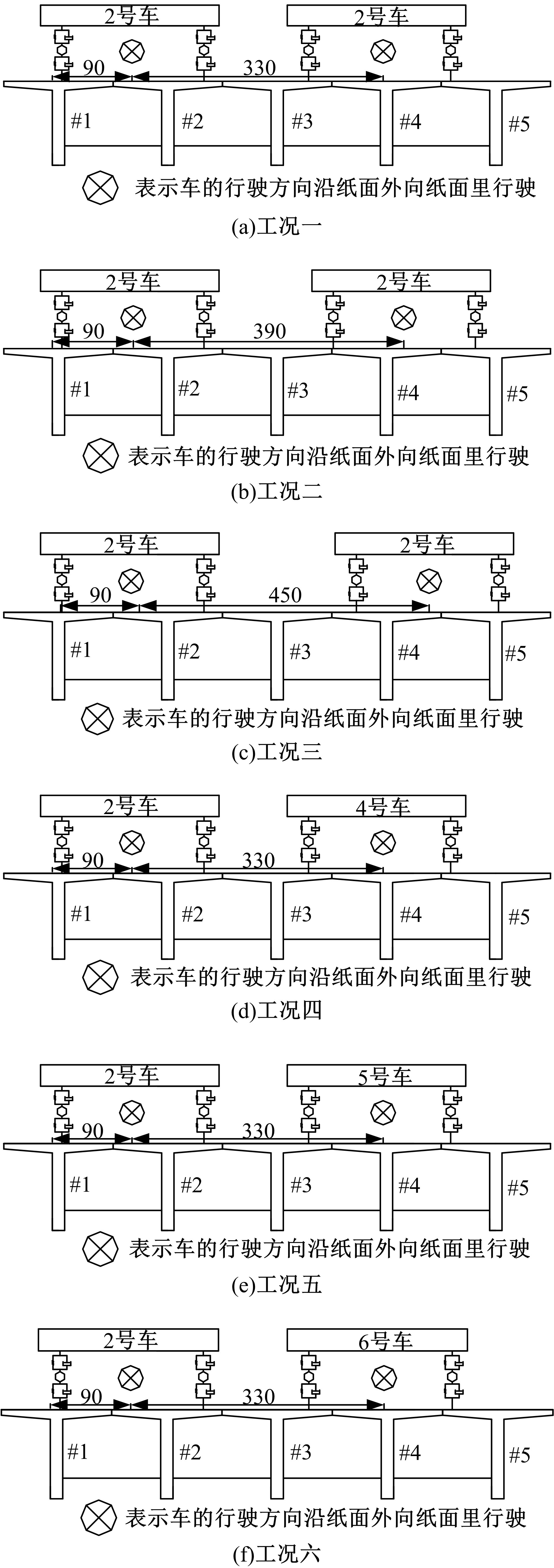
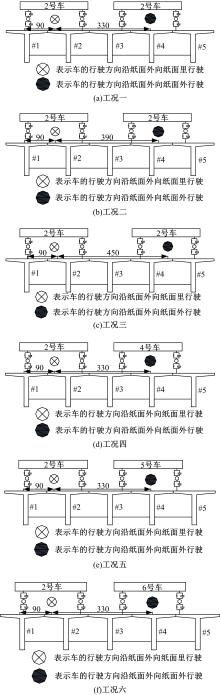
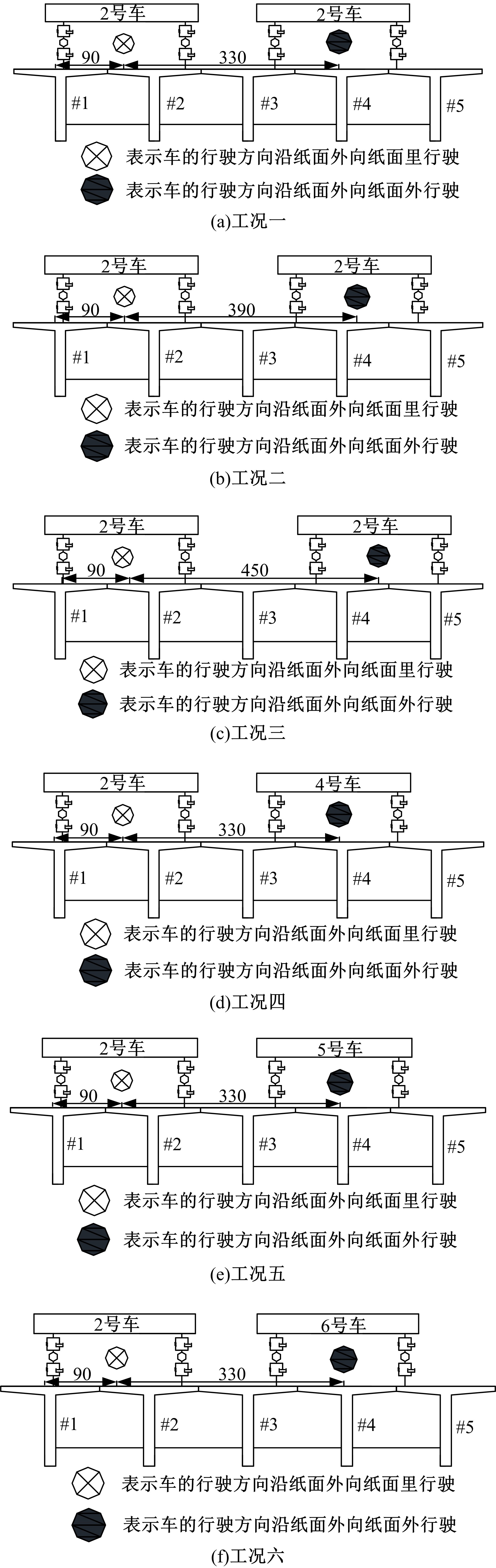
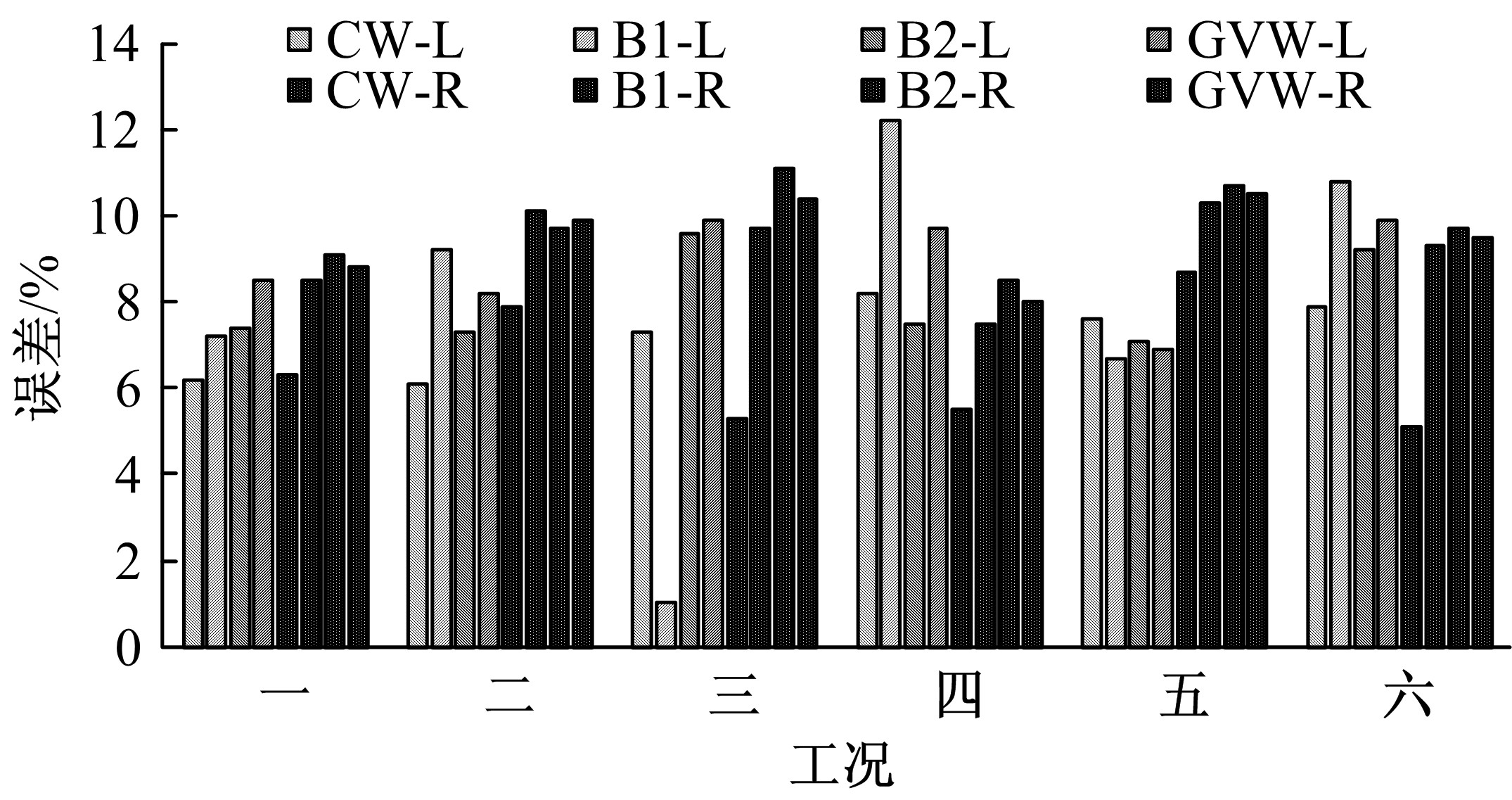
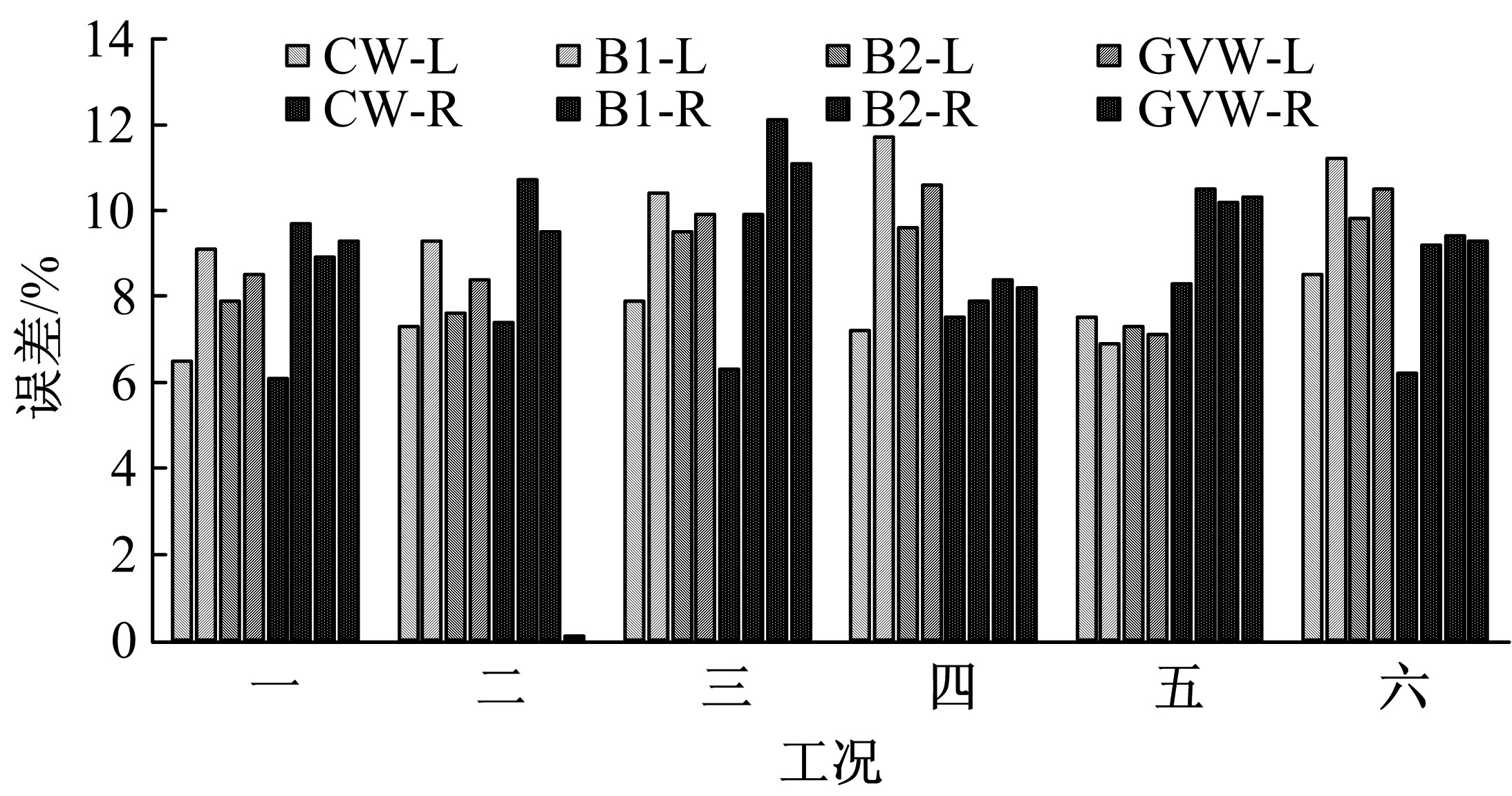
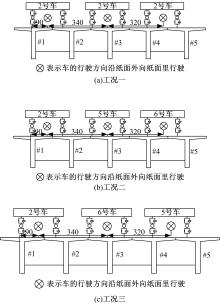
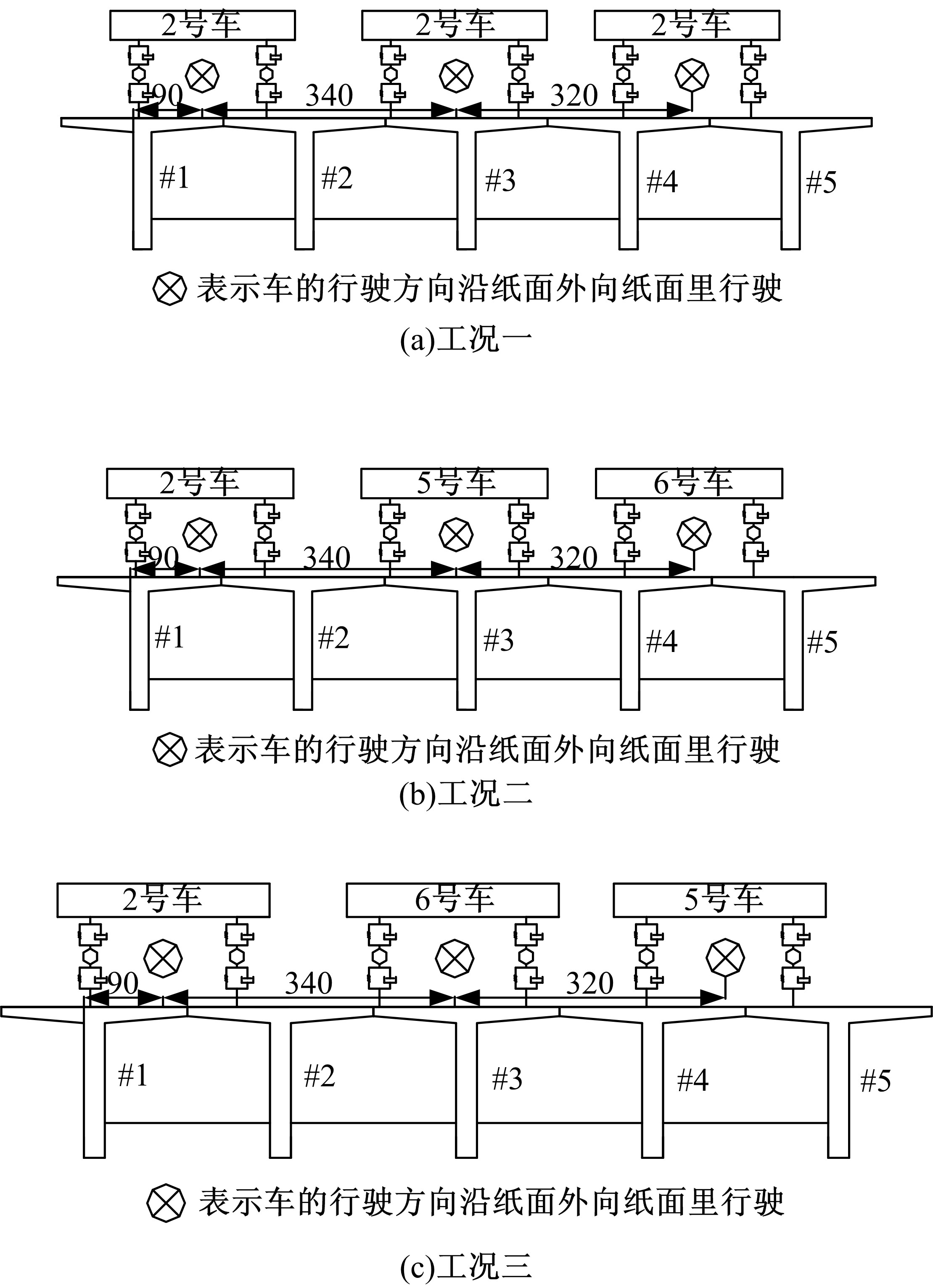
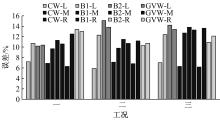
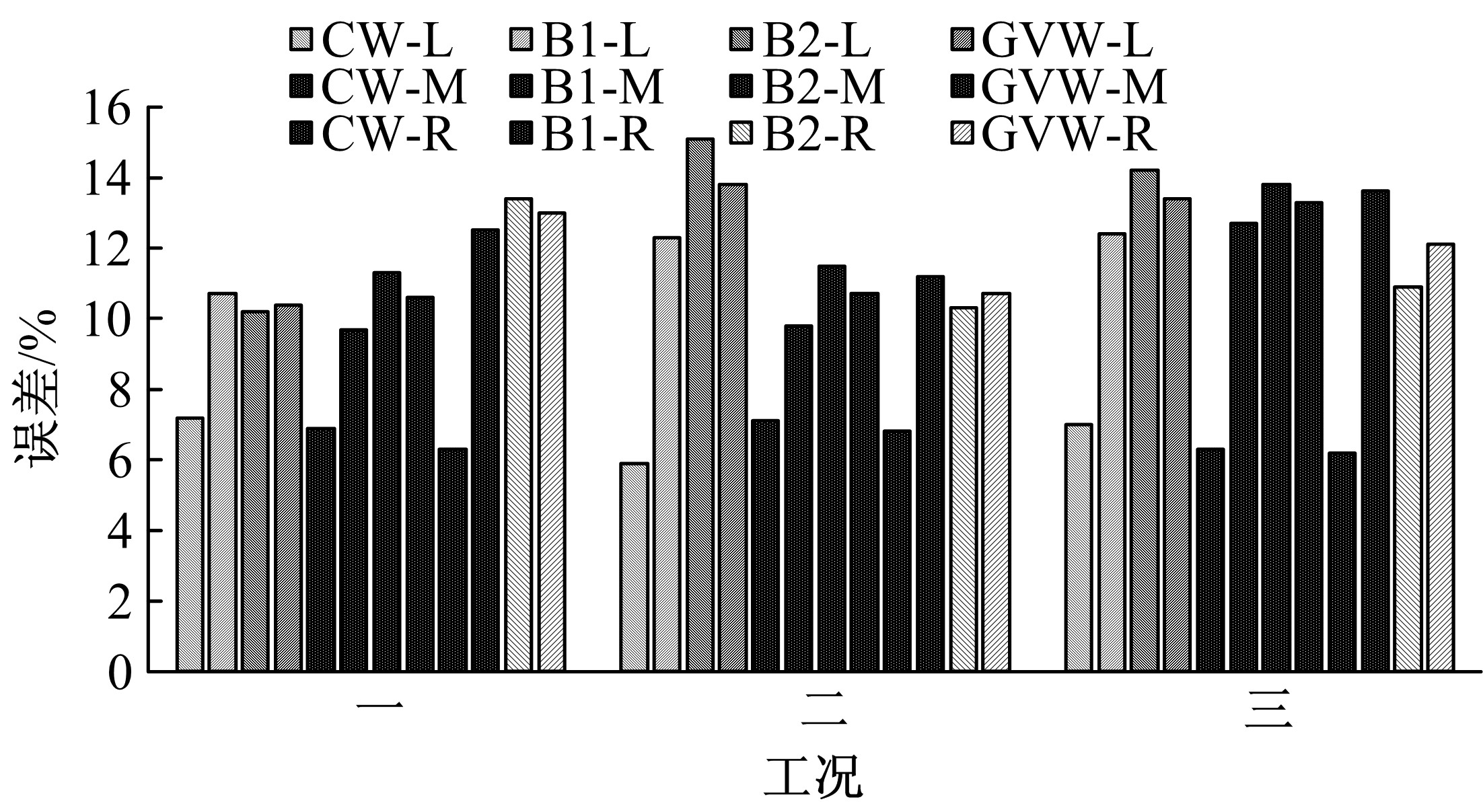
目前商用桥梁动态称重（BWIM）系统的研究主要集中在一维BWIM系统，多数只考虑单车过桥的情况，而实际交通中多车过桥的现象普遍存在。针对这一情况，提出了一种多车动态称重算法。以Moses轴重识别算法为基础，基于横桥向动力响应线和桥梁弯矩影响面，对单车以及多车过桥的横向位置及轴重等车辆信息进行识别，最后通过桥梁动态称重有限元仿真分析，研究单车过桥、两车过桥以及三车过桥等不同工况下本文算法的可靠性。结果表明：单车过桥、两车过桥以及三车过桥的情况下，随着车辆数目的增加，识别精度略有降低，车辆总重的识别最大误差在13%左右，车辆横向位置的识别误差在9%左右，识别精度满足工程实际需求，该算法可识别多车过桥时的车辆横向位置与轴重，具有发展成为商业BWIM系统的潜力。

关键词: 桥梁工程, 桥梁动态称重, 动力响应线, Moses算法

Abstract:

At present， the research on commercial bridge weigh-in-motion （BWIM） system was mainly focused on the one-dimensional BWIM system. Most of them only consider the situation of a single vehicle crossing the bridge， and the phenomenon of multiple vehicles crossing the bridge in actual traffic was common. Aiming at this situation， a multi-vehicle dynamic weighing algorithm was proposed. Based on the Moses axle weight recognition algorithm， based on the transverse bridge's dynamic response line and bridge bending moment influence surface， the vehicle information such as the lateral position and axle weight of the single and multiple vehicles crossing the bridge were identified， and the finite element was finally weighed by the bridge dynamics Simulation analysis is performed to study the reliability of the algorithm under different working conditions such as single vehicle crossing the bridge， two vehicles crossing the bridge and three vehicles crossing the bridge. The results shows that： under the conditions of single vehicle crossing the bridge， two vehicles crossing the bridge， and three vehicles crossing the bridge， with the increase of the number of vehicles， the recognition accuracy slightly decreases， the maximum error of the total vehicle weight recognition is about 13%， and the lateral position recognition The error is about 9%， and the recognition accuracy meets the actual needs of the project. The algorithm can identify the lateral position and axle weight of the vehicle when multiple vehicles cross the bridge， and has the potential to develop into a commercial BWIM system.

Key words: bridge engineering, bridge weigh-in-motion, dynamic response line, Moses algorithm

中图分类号:

U446.2

宫亚峰,宋加祥,谭国金,毕海鹏,刘洋,单承新. 多车桥梁动态称重算法[J]. 吉林大学学报(工学版), 2021, 51(2): 583-596.

Ya-feng GONG,Jia-xiang SONG,Guo-jin TAN,Hai-peng BI,Yang LIU,Cheng-xin SHAN. Multi⁃vehicle bridge weigh⁃in⁃motion algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(2): 583-596.

图/表 18

图1

图2

图3

表1

标定车参数列表"

参数	数值	参数	数值
$p s 1, p s 2$ /(N·m^-1)	$2.135 × 106$	$p s 3, p s 4$ /(N·m^-1)	$1.215 × 106$
$n s 1, n s 2$ /(N·s·m^-1)	$1.35 × 104$	$n s 3, n s 4$ /(N·s·m^-1)	$1.98 × 104$
$p t 1, p t 2$ /(N·m^-1)	$1.78 × 106$	$p t 3, p t 4$ /(N·m^-1)	$2.29 × 106$
$n t 1, n t 2$ /(N·s·m^-1)	$2.01 × 103$	$n t 3, n t 4$ /(N·s·m^-1)	$2.03 × 103$
$m t 1, m t 2$ /kg	$750$	$m t 3, m t 4$ /kg	$500$
$I v$ /（kg·m²）	$1.38 × 105$	$I r$ /（kg·m²）	$1.52 × 104$
$r 1$ /m	$2$	$r 2$ /m	$2$
$r 3$ /m	$0.95$	$m v$ /kg	$12 ? 500$

表1

表2

图4

图5

图6

图7

表3

图8

图9

图10

图11

图12

图13

图14

图15

参考文献 21

1	Moses F. Weigh-in-motion system using instrumented Bridges[J]. Transportation Engineering Journal, 1979, 105(3): 233-249.
2	Peters R J. Axway―a system to obtain vehicle axle weights[J]. Australia Road Research, 1984, 12(2): 17-29.
3	Peters R J. An unmanned and undetectable highway speed vehicle weighing system[J]. Australian Road Research Board Proceedings, 1986, 1(1): 70-83.
4	Commission European. Weight-in-motion of axles and vehicles for Europe (WAVE): general report[R]. Paris: LCPC, 2001.
5	Commission European. Weight-in-motion of axles and vehicles for Europe (WAVE): report of work package 1.2-Bridge WIM systems (B-WIM)[R]. Dublin: University College Dublin, 2001.
6	Jacob B, O'Brien E J. Weigh-in-motion: recent developments in Europe[C]∥4th International Conference on Weigh-In-Motion, Taipei, 2005: 90-94.
7	Rowley C W, Gonz A A, O'Brien E J, et a1. Comparison of conventional and regularized bridge weigh-in-motion algorithms[C]∥5th International Conference on Weigh-in-Motion, Paris, 2008: 12-13.
8	王林军. 正则化方法及其在动态载荷识别中的应用[D]. 长沙: 湖南大学机械与载运工程学院, 2011.
	Wang Lin-jun. Regularization method and its application in dynamic load identification[D]. Changsha: School of Mechanical and Transportation Engineering, Hunan University, 2011.
9	龙波. 移动车辆轴重识别MOSES算法在宽桥中的应用研究[D]. 长沙: 湖南大学土木工程学院, 2014.
	Long Bo. Application of MOSES algorithm for axle weight identification of moving vehicles in wide bridges[D]. Changsha: School of Civil Engineering, Hunan University, 2014.
10	邓露, 施海, 何维, 等. 基于虚拟简支梁法的桥梁动态称重研究[J]. 振动与冲击, 2018, 37(15): 209-215.
	Deng Lu, Shi Hai, He Wei, et al. Research on dynamic weighing of bridges based on virtual simply supported beam method[J]. Vibration and Shock, 2018, 37(15): 209-215.
11	Zolghadri N, Halling M W, Johnson N, et al. Field verification of simplified bridge weigh-in-motion techniques[J]. Journal of Bridge Engineering, 2016, 21(10): 4016063.
12	Quilligan M. Bridge weigh-in-motion: development of a 2-D multi-vehicle algorithm[J]. Trita-BKN Bulletin, 2003, 1(1): 23-35.
13	刘洋. 基于Moses算法的单车及多车动态称重算法研究[D]. 长春: 吉林大学交通学院, 2019.
	Liu Yang. Study on the BWIM algorithm of a vehicle or multi-vehicles based on the Moses algorithm[D]. Changchun: College of Transportation, Jilin University, 2019.
14	Zhao H, Uddin N, O'Brien E J, et al. Identification of vehicular axle weights with a bridge weigh-in-motion system considering transverse distribution of wheel loads[J]. Journal of Bridge Engineering, 2013, 19(3): 04013008.
15	Tikhonov A N, Arsenin V Y. Solutions of ill-posed problems[J]. Mathematics of Computation, 1977, 32(144): 1-258.
16	汤海燕, 蔡晶. 桥梁结构影响面与影响线的比较研究[C]∥江苏省力学学会青年力学论坛, 南京, 2005: 104-108.
17	李希. 点云数据处理及规则曲面拟合[D]. 太原: 中北大学计算机科学与技术学院, 2017.
	Li Xi. Point cloud data processing and regular surface fitting[D]. Taiyuan: College of Computer Science and Technology, North University of China, 2017.
18	刘福寿. 基于车桥耦合振动的混凝土简支梁桥动力特性研究[D]. 长春: 吉林大学交通学院, 2009.
	Liu Fu-shou. Study on the dynamic characteristics of a simply supported concrete beam bridge based on vehicle-bridge coupling vibration[D]. Changchun: College of Transportation, Jilin University, 2009.
19	Huang D, Wang T L. Impact analysis of cable-stayed bridge[J].Computers and Structures, 1992, 43(5): 897-908.
20	谭国金, 刘子煜, 魏海斌, 等. 偏心直线预应力筋简支梁自振频率计算方法[J]. 吉林大学学报: 工学版, 2016, 46(3): 798-803.
	Tan Guo-jin, Liu Zi-yu, Wei Hai-bin, et al. Calculation method of natural vibration frequency of simply supported beam with eccentric linear prestressed tendons[J]. Journal of Jilin University (Engineering and Technology Edition), 2016, 46(3): 798-803.
21	宫亚峰, 何钰龙, 谭国金, 等. 三跨独柱连续曲线梁桥抗倾覆稳定性分析[J]. 吉林大学学报: 工学版, 2018, 48(1): 113-120.
	Gong Ya-feng, He Yu-long, Tan Guo-jin, et al. Three-span single-column continuous curve beam bridge anti-overturning stability analysis[J]. Journal of Jilin University (Engineering and Technology Edition), 2018, 48(1): 113-120.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

路面等级	路面不平整度系数/10^-6m³
路面等级	下限	上限	几何平均
A	—	32	16
B	32	128	64
C	128	512	256
D	512	2 048	1 024
E	2 048	8 192	4 096
F	8 192	32 768	16 384
G	32 768	131 072	65 536
H	131 072	—	262 144

车辆编号	类型	轴距/m	前轴/t	后轴/t	总重/t
1	两轴车	4.27	5.8	6.7	12.5
2	两轴车	4.27	7.0	8.0	15.0
3	两轴车	4.27	8.3	9.5	17.8
4	两轴车	4.27	9.4	10.6	20.0
5	两轴车	4.27	4.8	5.7	10.5
6	两轴车	4.27	10.8	12.2	23.0

[1]	孔庆雯,谭国金,王龙林,王勇,魏志刚,刘寒冰. 基于有限元方法的裂缝箱梁桥自振特性分析[J]. 吉林大学学报(工学版), 2021, 51(1): 225-232.
[2]	陈华,陈耀嘉,谢斌,王鹏凯,邓朗妮. CFRP筋粘结式锚固体系界面失效演化机制及粘结强度计算[J]. 吉林大学学报(工学版), 2020, 50(5): 1698-1708.
[3]	宫亚峰,宋加祥,毕海鹏,谭国金,胡国海,林思远. 装配式箱涵结构缩尺模型静载试验及有限元分析[J]. 吉林大学学报(工学版), 2020, 50(5): 1728-1738.
[4]	高昊,王君杰,刘慧杰,王剑明. 连续梁桥地震行为可控设计准则及实用装置[J]. 吉林大学学报(工学版), 2020, 50(5): 1718-1727.
[5]	蒲黔辉,刘静文,赵刚云,严猛,李晓斌. 高性能树脂混凝土加固混凝土偏压柱承载力理论分析[J]. 吉林大学学报(工学版), 2020, 50(2): 606-612.
[6]	张云龙,郭阳阳,王静,梁东. 钢-混凝土组合梁的固有频率及其振型[J]. 吉林大学学报(工学版), 2020, 50(2): 581-588.
[7]	王伯昕,杨海涛,王清,高欣,陈小旭. 基于补充改进集合经验模态分析法⁃多尺度排列熵分析桥梁振动信号优化滤波方法[J]. 吉林大学学报(工学版), 2020, 50(1): 216-226.
[8]	张淼,钱永久,张方,朱守芹. 基于增大截面法的混凝土加固石拱桥空间受力性能试验分析[J]. 吉林大学学报(工学版), 2020, 50(1): 210-215.
[9]	贾毅,赵人达,王永宝,李福海. 多跨长联连续梁桥粘滞阻尼器参数敏感性分析[J]. 吉林大学学报(工学版), 2019, 49(6): 1871-1883.
[10]	钟春玲,梁东,张云龙,王静. 体外预应力加固简支梁自振频率计算[J]. 吉林大学学报(工学版), 2019, 49(6): 1884-1890.
[11]	白伦华,沈锐利,张兴标,王路. 自锚式悬索桥的面内稳定性[J]. 吉林大学学报(工学版), 2019, 49(5): 1500-1508.
[12]	赵金钢,张明,占玉林,谢明志. 基于塑性应变能密度的钢筋混凝土墩柱损伤准则[J]. 吉林大学学报(工学版), 2019, 49(4): 1124-1133.
[13]	万世成,黄侨,关健,郭赵元. 预应力碳纤维板加固钢⁃混凝土组合连续梁负弯矩区试验[J]. 吉林大学学报(工学版), 2019, 49(4): 1114-1123.
[14]	李万恒,申林,王少鹏,赵尚传. 基于多阶段分区域动力测试的桥梁结构损伤评估[J]. 吉林大学学报(工学版), 2019, 49(3): 773-780.
[15]	惠迎新,毛明杰,刘海峰,张尚荣. 跨断层桥梁结构地震响应影响[J]. 吉林大学学报(工学版), 2018, 48(6): 1725-1734.

多车桥梁动态称重算法

Multi⁃vehicle bridge weigh⁃in⁃motion algorithm

RICH HTML

PDF (PC)

摘要/Abstract

引用本文

使用本文

图/表 18

参考文献 21

相关文章 15

Metrics

本文评价

推荐阅读 0