双柱式高墩桥梁整体稳定性的实用算法

doi:10.13229/j.cnki.jdxbgxb.20210784

吉林大学学报(工学版) ›› 2023, Vol. 53 ›› Issue (4): 1105-1111.doi: 10.13229/j.cnki.jdxbgxb.20210784

• 交通运输工程·土木工程 • 上一篇

双柱式高墩桥梁整体稳定性的实用算法

兰树伟¹(),周东华²(),陈旭¹,莫南明¹

^1.昆明学院建筑工程学院，昆明 650214
^2.昆明理工大学建筑工程学院，昆明 650500

收稿日期:2021-08-13 出版日期:2023-04-01 发布日期:2023-04-20
通讯作者: 周东华 E-mail:lanshuwei2000@163.com;stahlverbundbau@aliyun.com
作者简介:兰树伟（1986-），男，讲师，博士.研究方向：混凝土结构和组合结构.E?mail： lanshuwei2000@163.com
基金资助:
国家自然科学基金项目(51868034);云南省地方本科高校基础研究联合专项资金青年项目(202101BA070001-003);昆明学院引进人才科研项目(XJ20210029)

Practical calculation method for the critical bearing capacity of double column bridge with high piers

Shu-wei LAN¹(),Dong-hua ZHOU²(),Xu CHEN¹,Nan-ming MO¹

^1.College of Architecture and Civil Engineering，Kunming University，Kunming 650214，China
^2.Faculty of Civil Engineering and Mechanics，Kunming University of Science and Technology，Kunming 650500，China

Received:2021-08-13 Online:2023-04-01 Published:2023-04-20
Contact: Dong-hua ZHOU E-mail:lanshuwei2000@163.com;stahlverbundbau@aliyun.com

摘要/Abstract

摘要：

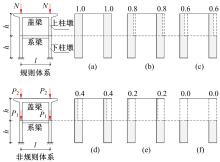
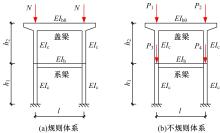
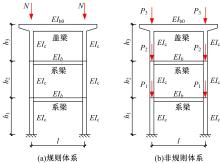
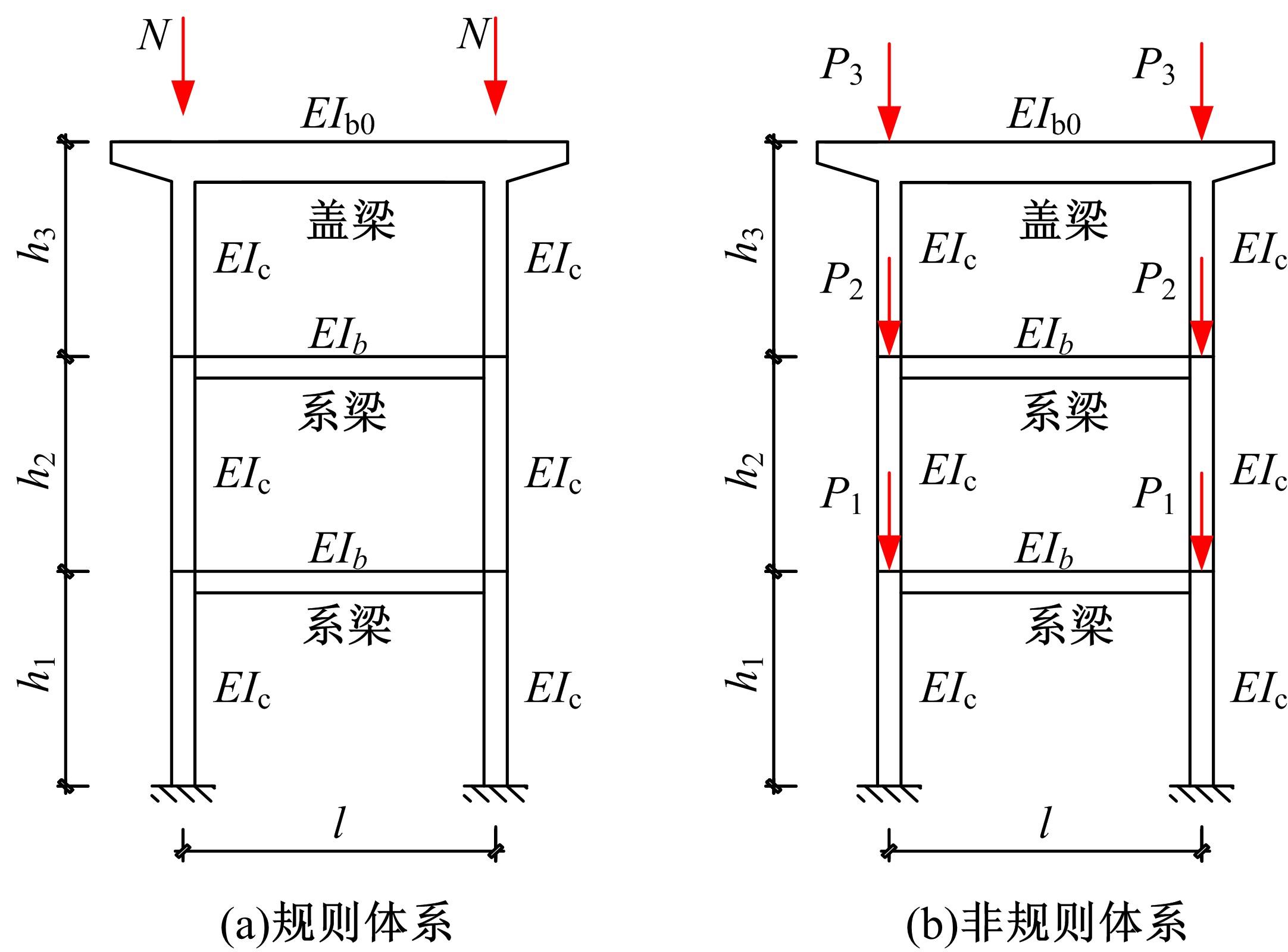
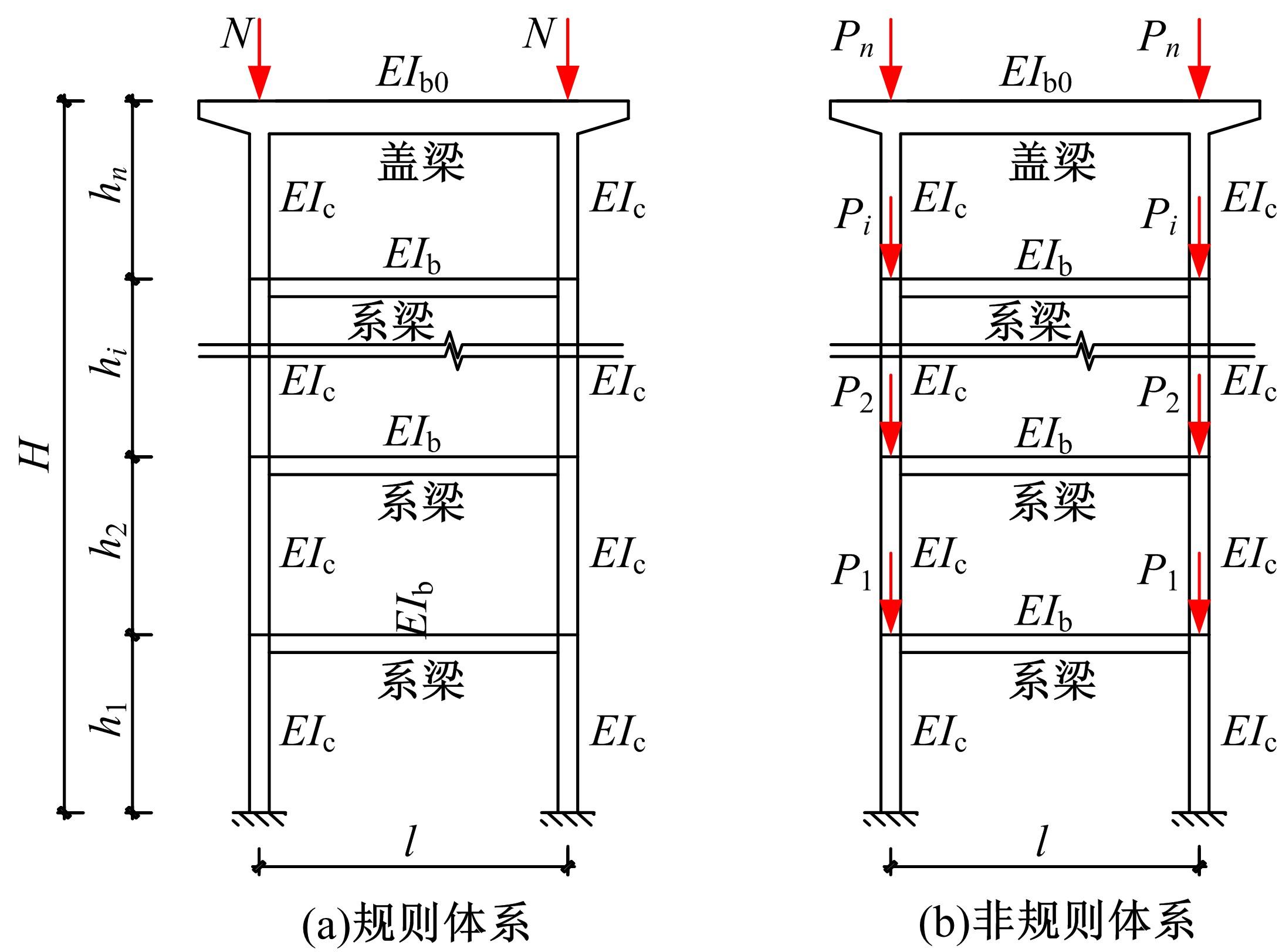
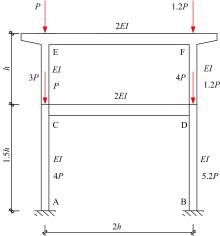
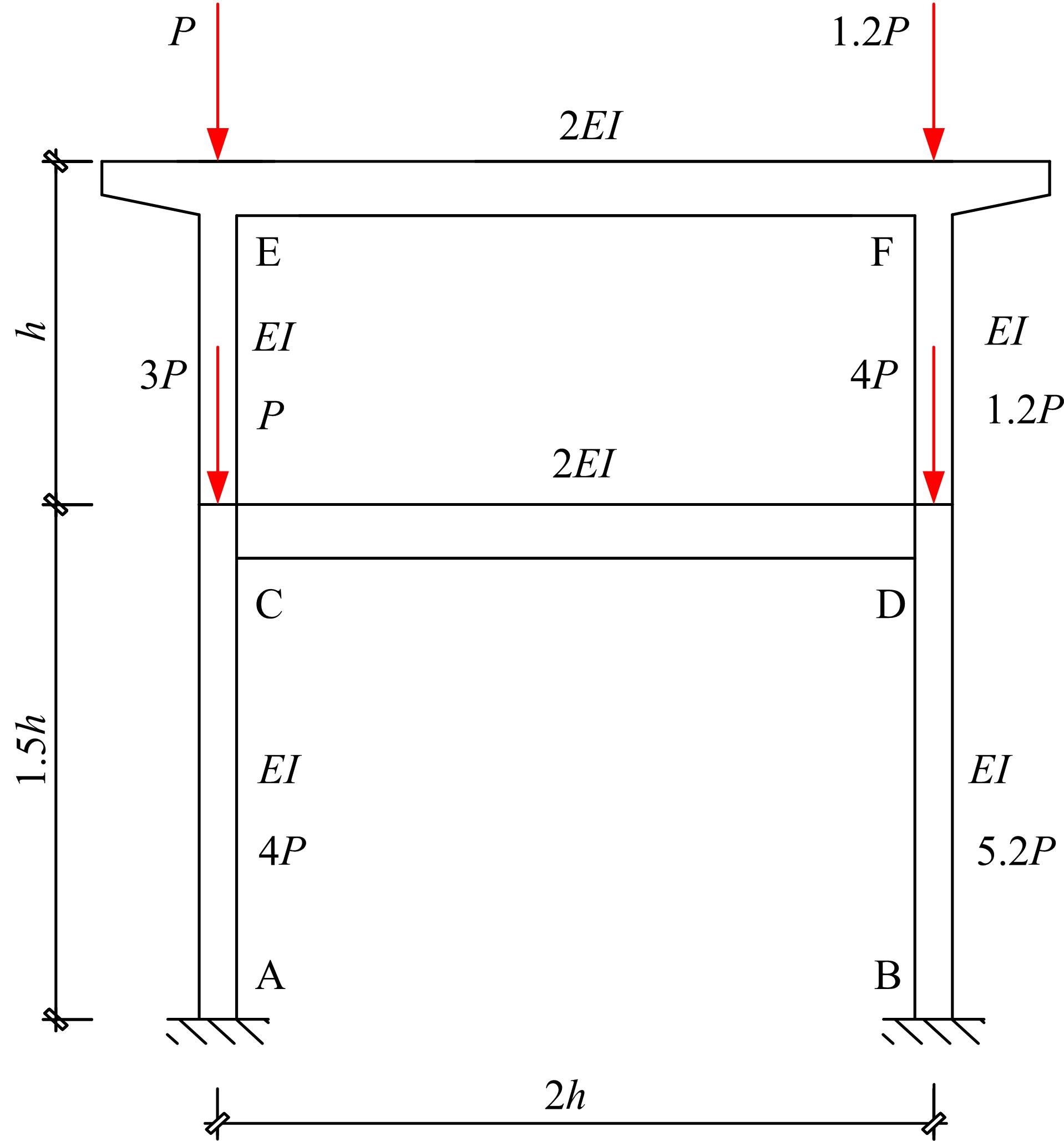
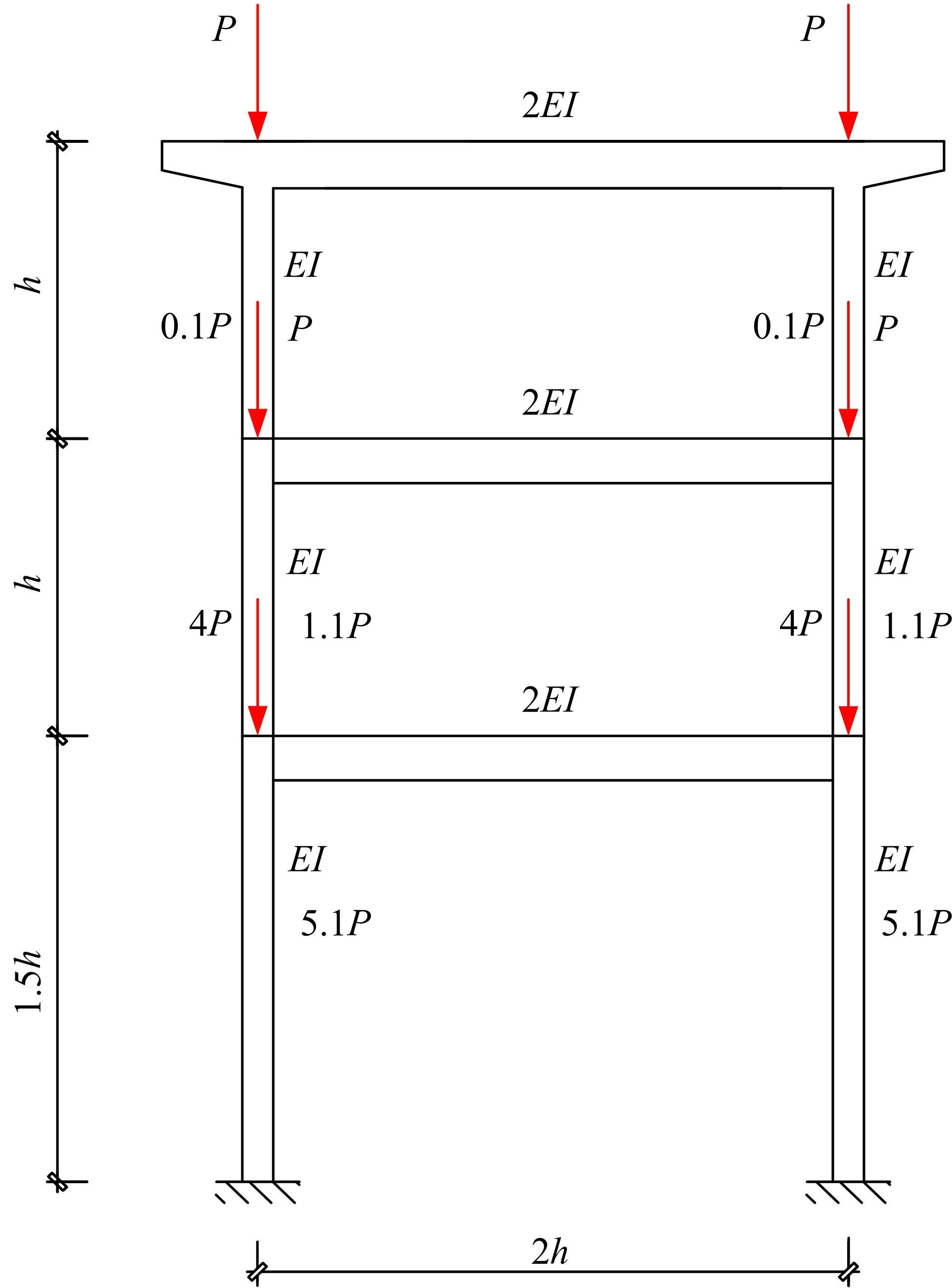
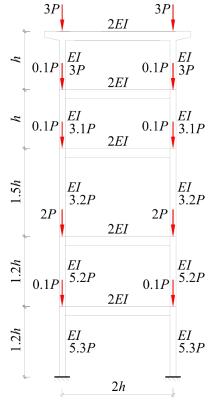
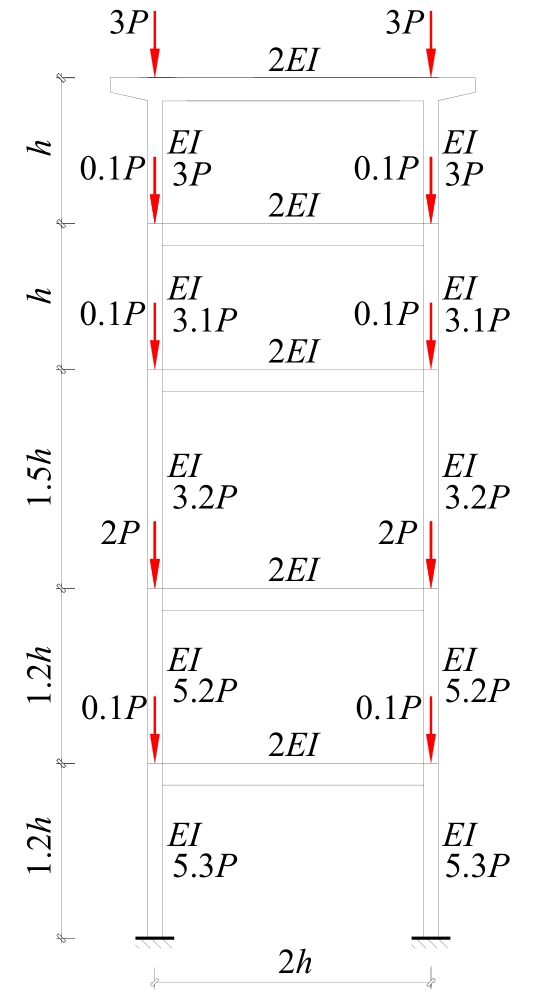
从受压柱刚度激活程度出发，研究了轴力面积大小对非规则双层双柱式高墩桥梁体系临界力的影响，并找到了一些规律，建立了相应的双柱式高墩桥梁横桥向临界承载力的计算方法，使得双柱式高墩桥梁临界力的求解大为简化。推导了双柱式高墩桥梁横桥向结构临界力的计算公式，这些公式能考虑柱墩之间系梁的影响，弥补规范计算长度系数法的不足，为桥梁工程设计提供了快速计算的方法和公式。最后，选取了3个算例进行有限元计算验证，计算结果表明：该方法具有很好的精度及准确性，适用于任意节点荷载分布，可供工程设计和理论计算使用。

关键词: 桥梁工程, 双柱式高墩, 轴力面积比, 整体稳定, 临界力, 计算长度系数

Abstract:

Based on the stiffness activation of the compression column， the influence of the axial force area on the critical bearing capacity of double column pier with two-story is studied. Some rules are found and the corresponding calculation method of the horizontal critical bearing capacity of double column bridge with high piers is established， so that the solution of the critical force of column bridge with high piers is greatly simplified. This paper deduces the calculation formula of the horizontal critical force for double column bridge with high piers. These formulas can take into account the influence of the tie beams between the piers， which can make up for the deficiency of the standardized calculation length coefficient method and provide a fast calculation method and formula for bridge engineering design. Finally， three examples are selected for finite element calculation. The calculation results show that this method has good precision and accuracy， which can be suitable for arbitrary node load distribution and used for engineering design and theoretical calculation.

Key words: bridge engineering, double column pier, axial force area ratio, overall stability, critical force, calculating length coefficient

中图分类号:

U441.2

兰树伟,周东华,陈旭,莫南明. 双柱式高墩桥梁整体稳定性的实用算法[J]. 吉林大学学报(工学版), 2023, 53(4): 1105-1111.

Shu-wei LAN,Dong-hua ZHOU,Xu CHEN,Nan-ming MO. Practical calculation method for the critical bearing capacity of double column bridge with high piers[J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(4): 1105-1111.

图/表 10

图1

图2

图3

图4

图5

表1

柱墩稳定承载力及计算长度系数对比结果（算例1）"

柱	分项 $P E = π 2 E I / h 2$	规范法①	本文方法②	Ansys③	①/③	②/③
AC	$P c r / P E$	0.278	0.332	0.320	0.869	1.038
BD		0.278	0.432	0.416	0.669	1.038
CE		0.491	0.083	0.080	6.138	1.038
DF		0.491	0.100	0.096	5.115	1.042
AC	$μ$	1.265	1.157	1.179	1.073	0.981
BD		1.265	1.014	1.034	1.223	0.981
CE		1.427	3.471	3.535	0.404	0.982
DF		1.427	3.162	3.227	0.442	0.980

表1

图6

表2

柱墩稳定承载力及计算长度系数对比结果（算例2）"

柱	分项 $P E = π 2 E I / h 2$	规范法①	本文方法②	Ansys③	①/③	②/③
一层	$P c r / P E$	0.278	0.383	0.372	0.747	1.030
二层		0.410	0.083	0.080	5.125	1.038
三层		0.466	0.075	0.073	6.384	1.028
一层	$μ$	1.265	1.077	1.093	1.157	0.985
二层		1.562	3.471	3.535	0.442	0.982
三层		1.465	3.651	3.701	0.396	0.986

表2

图7

表3

柱墩稳定承载力及计算长度系数对比结果（算例3）"

柱	分项 $P E = π 2 E I / h 2$	规范法①	本文方法②	Ansys③	①/③	②/③
一层	$P c r / P E$	0.434	0.364	0.374	1.160	0.973
二层		0.309	0.357	0.367	0.842	0.973
三层		0.198	0.220	0.226	0.876	0.973
四层		0.410	0.213	0.219	1.872	0.973
五层		0.466	0.206	0.212	2.198	0.972
一层	$μ$	1.265	1.381	1.363	0.928	1.013
二层		1.499	1.395	1.376	1.089	1.014
三层		1.499	1.421	1.402	1.069	1.014
四层		1.562	2.167	2.137	0.731	1.014
五层		1.465	2.203	2.172	0.674	1.014

表3

参考文献 13

1	公路钢筋混凝土及预应力混凝土桥涵设计规范 [S].
2	. 钢结构设计标准 [S].
3	Podolny W, Muller J M. Construction and Design of Prestressed Concrete Segmental Bridges[M] .London: Wiley, 1982.
4	Cai Z K, Wang Z. Experimental testing and modeling of precast segmental bridge columns with Hybrid normal-and high-strength steel rebars[J].Construction & Building Materials, 2018, 166: 945-955.
5	王兵见,赵航,彭卫兵,等.独柱墩梁桥横向稳定计算理论与验证[J].中国公路学报, 2017, 30(9): 93-100.
	Wang Bing-jian, Zhao Hang, Peng Wei-bing, et al. Lateral stability calculation theory and verification of single-column girder bridge[J]. China Journal of Highway and Transport, 2017, 30(9): 93-100.
6	熊文,鲁圣弟,龚玄,等. 独柱墩梁桥倾覆临界状态分析及规范法的适用性[J]. 中国公路学报, 2018, 31(3): 49-58.
	Xiong Wen, Lu Sheng-di, Gong Xuan, et al. Gritical condition analysis of overturned bridges with single-column piers and applicability of design standards[J]. Journal of Dalian University of Technology, 2018, 31(3): 49-58.
7	童根树. 钢结构的平面内稳定[M]. 北京:中国建筑工业出版社, 2005.
8	郝际平,田炜烽,王先铁.多层有侧移框架整体稳定的简便计算方法[J]. 建筑结构学报, 2011, 32(11): 183-188.
	Hao Ji-ping, Tian Wei-feng, Wang Xian-tie. Simple calculation method for overall stability of multi-story sway frame[J]. Journal of Building Structures, 2011,32(11): 183-188.
9	兰树伟,周东华,双超,等.有侧移框架临界承载力的实用计算方法[J]. 振动与冲击,2019, 38(11):180-186, 202.
	Lan Shu-wei, Zhou Dong-hua, Shuang Chao,et al. Practical calculation method for the critical bearing capacity of sway frame[J]. Journal of Vibration and Shock, 2019,38(11): 180-186, 202.
10	Gunther Lohse. Einfuhrung in Das Knicken und Kippen[M]. Düsseldorf: Werner-Verlag GmbH, 1983:68-13.
11	Adolf Lubbertus Bouma. Mechanik Schlanker Tragwerke: Ausgewählte Beispiele der Praxis[M]. Berlin: Springer-Verlag Heidelberg, 1993.
12	耿旭阳,周东华. 确定受压柱计算长度的通用图表[J].工程力学, 2014, 31(8): 154-160, 174.
	Geng Xu-yang, Zhou Dong-hua. Universal charts for determining the effective length of compression columns[J]. Engineering Mechanics, 2014, 31(8): 154-160, 174.
13	兰树伟,周东华,双超. 基于挠度法的有侧移框架临界力计算方法[J]. 华中科技大学学报: 自然科学版, 2019, 47(5): 122-127.
	Lan Shu-wei, Zhou Dong-hua, Shuang Chao. Calculation method of critical force of sway frame based on deflection method[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2019, 47(5): 122-127.

相关文章 15

[1]	孙琪凯,张楠,刘潇,周子骥. 基于Timoshenko梁理论的钢-混组合梁动力折减系数[J]. 吉林大学学报(工学版), 2023, 53(2): 488-495.
[2]	叶华文,段智超,刘吉林,周渝,韩冰. 正交异性钢⁃混组合桥面的轮载扩散效应[J]. 吉林大学学报(工学版), 2022, 52(8): 1808-1816.
[3]	王立峰,肖子旺,于赛赛. 基于Bayesian网络的多塔斜拉桥挂篮系统风险分析的新方法[J]. 吉林大学学报(工学版), 2022, 52(4): 865-873.
[4]	张彦玲,王灿,张旭,王昂洋,李运生. 不同吊杆形式悬索桥人致振动分析及舒适度评价[J]. 吉林大学学报(工学版), 2022, 52(11): 2644-2652.
[5]	钟昌均,王忠彬,柳晨阳. 悬索桥主索鞍承载力影响因素及结构优化[J]. 吉林大学学报(工学版), 2021, 51(6): 2068-2078.
[6]	陈巍,万田保,王忠彬,厉萱,沈锐利. 悬索桥主缆除湿的内部送气管道设计与性能[J]. 吉林大学学报(工学版), 2021, 51(5): 1749-1755.
[7]	郭殊伦,钟铁毅,闫志刚. 大跨度斜拉桥拉索的抖振响应计算方法[J]. 吉林大学学报(工学版), 2021, 51(5): 1756-1762.
[8]	高凯,刘纲. 全局临界强度分枝-约界法的有效强度改进[J]. 吉林大学学报(工学版), 2021, 51(2): 597-603.
[9]	宫亚峰,宋加祥,谭国金,毕海鹏,刘洋,单承新. 多车桥梁动态称重算法[J]. 吉林大学学报(工学版), 2021, 51(2): 583-596.
[10]	孔庆雯,谭国金,王龙林,王勇,魏志刚,刘寒冰. 基于有限元方法的裂缝箱梁桥自振特性分析[J]. 吉林大学学报(工学版), 2021, 51(1): 225-232.
[11]	陈华,陈耀嘉,谢斌,王鹏凯,邓朗妮. CFRP筋粘结式锚固体系界面失效演化机制及粘结强度计算[J]. 吉林大学学报(工学版), 2020, 50(5): 1698-1708.
[12]	宫亚峰,宋加祥,毕海鹏,谭国金,胡国海,林思远. 装配式箱涵结构缩尺模型静载试验及有限元分析[J]. 吉林大学学报(工学版), 2020, 50(5): 1728-1738.
[13]	高昊,王君杰,刘慧杰,王剑明. 连续梁桥地震行为可控设计准则及实用装置[J]. 吉林大学学报(工学版), 2020, 50(5): 1718-1727.
[14]	蒲黔辉,刘静文,赵刚云,严猛,李晓斌. 高性能树脂混凝土加固混凝土偏压柱承载力理论分析[J]. 吉林大学学报(工学版), 2020, 50(2): 606-612.
[15]	张云龙,郭阳阳,王静,梁东. 钢-混凝土组合梁的固有频率及其振型[J]. 吉林大学学报(工学版), 2020, 50(2): 581-588.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

双柱式高墩桥梁整体稳定性的实用算法

Practical calculation method for the critical bearing capacity of double column bridge with high piers

RICH HTML

PDF (PC)

摘要/Abstract

引用本文

使用本文

图/表 10

参考文献 13

相关文章 15

Metrics

本文评价

推荐阅读 0