基于多目标遗传算法的二自由度动力吸振器优化设计

doi:10.13229/j.cnki.jdxbgxb20180924

摘要/Abstract

摘要：

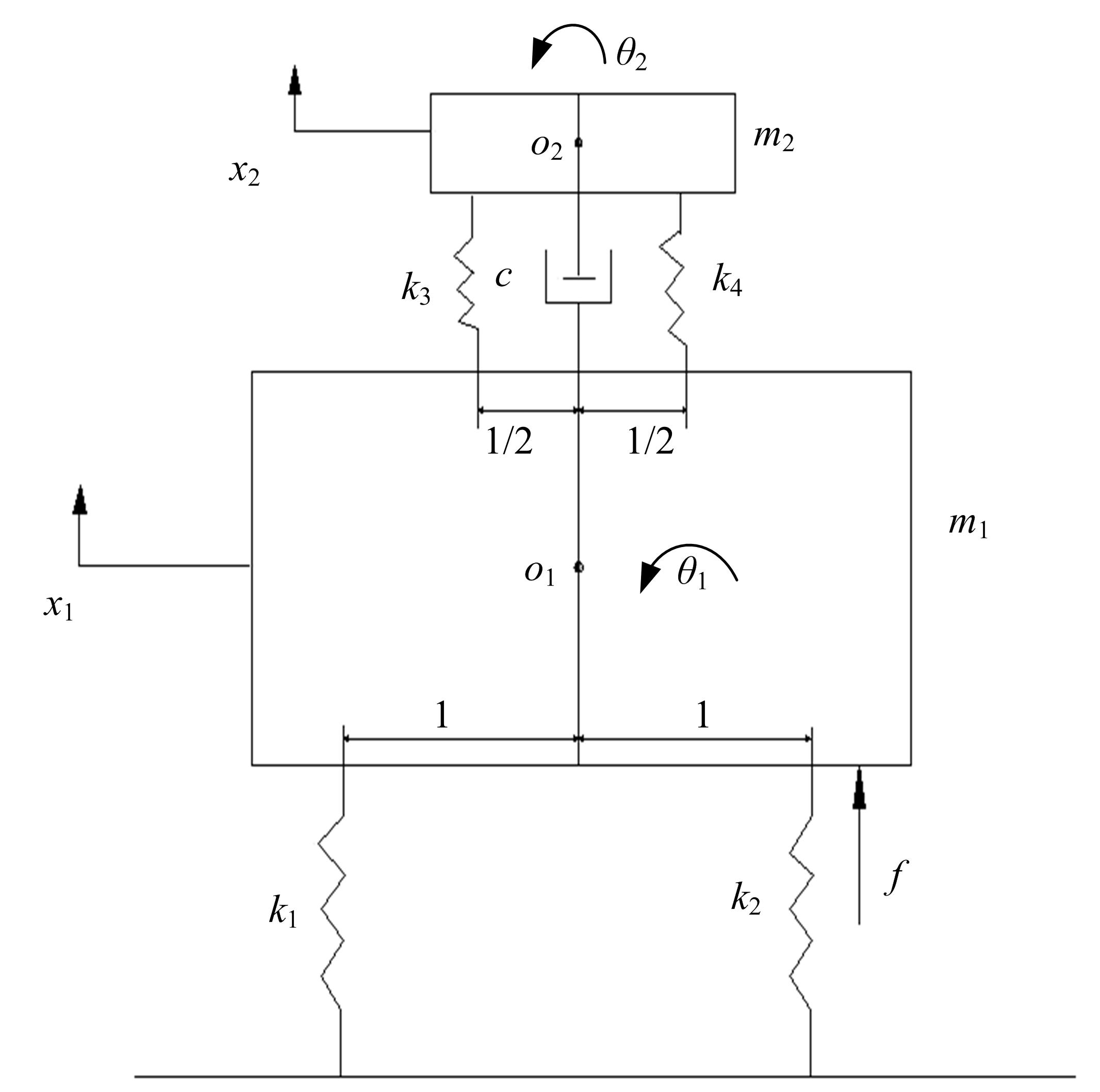
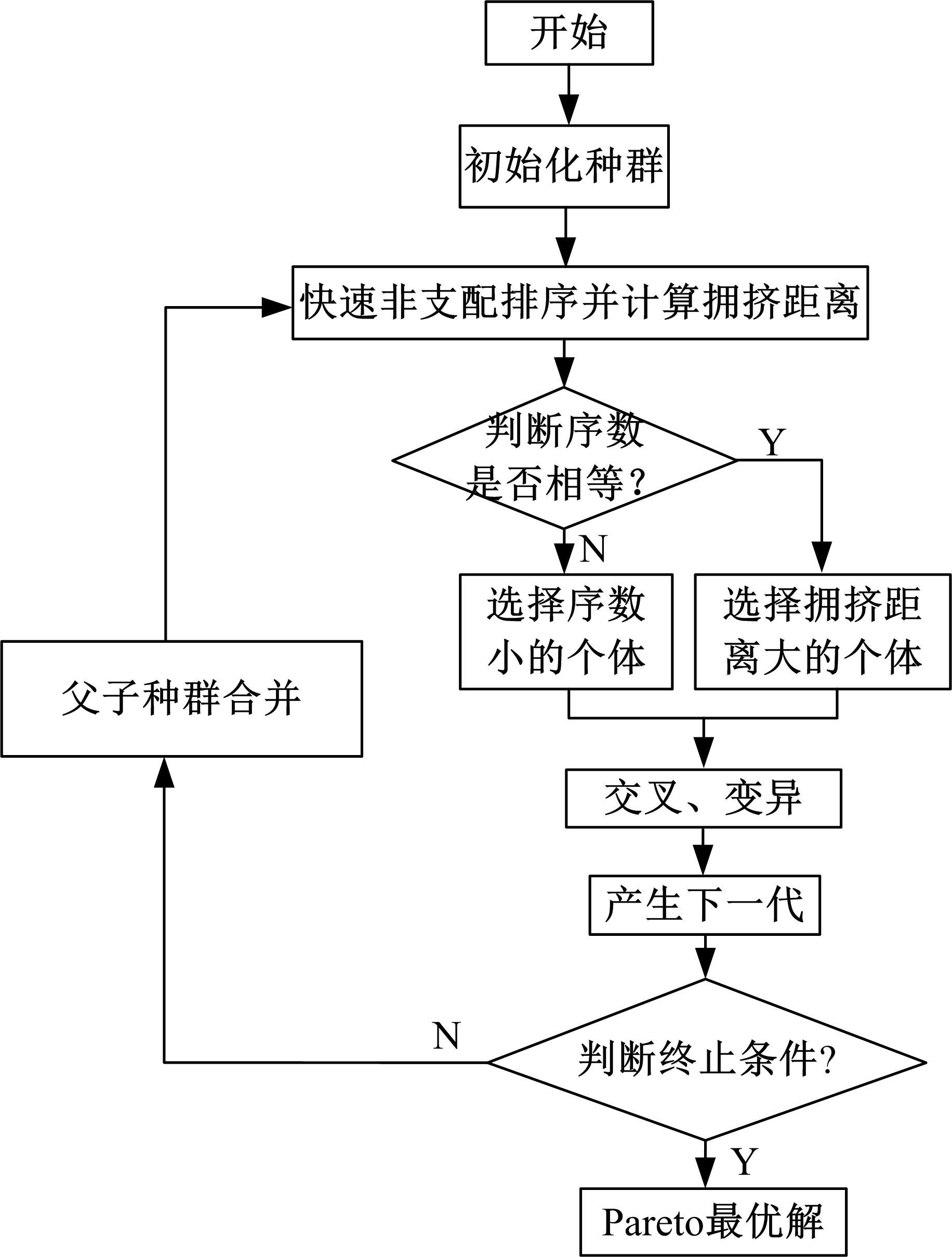
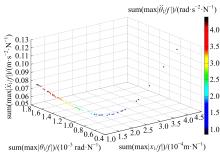
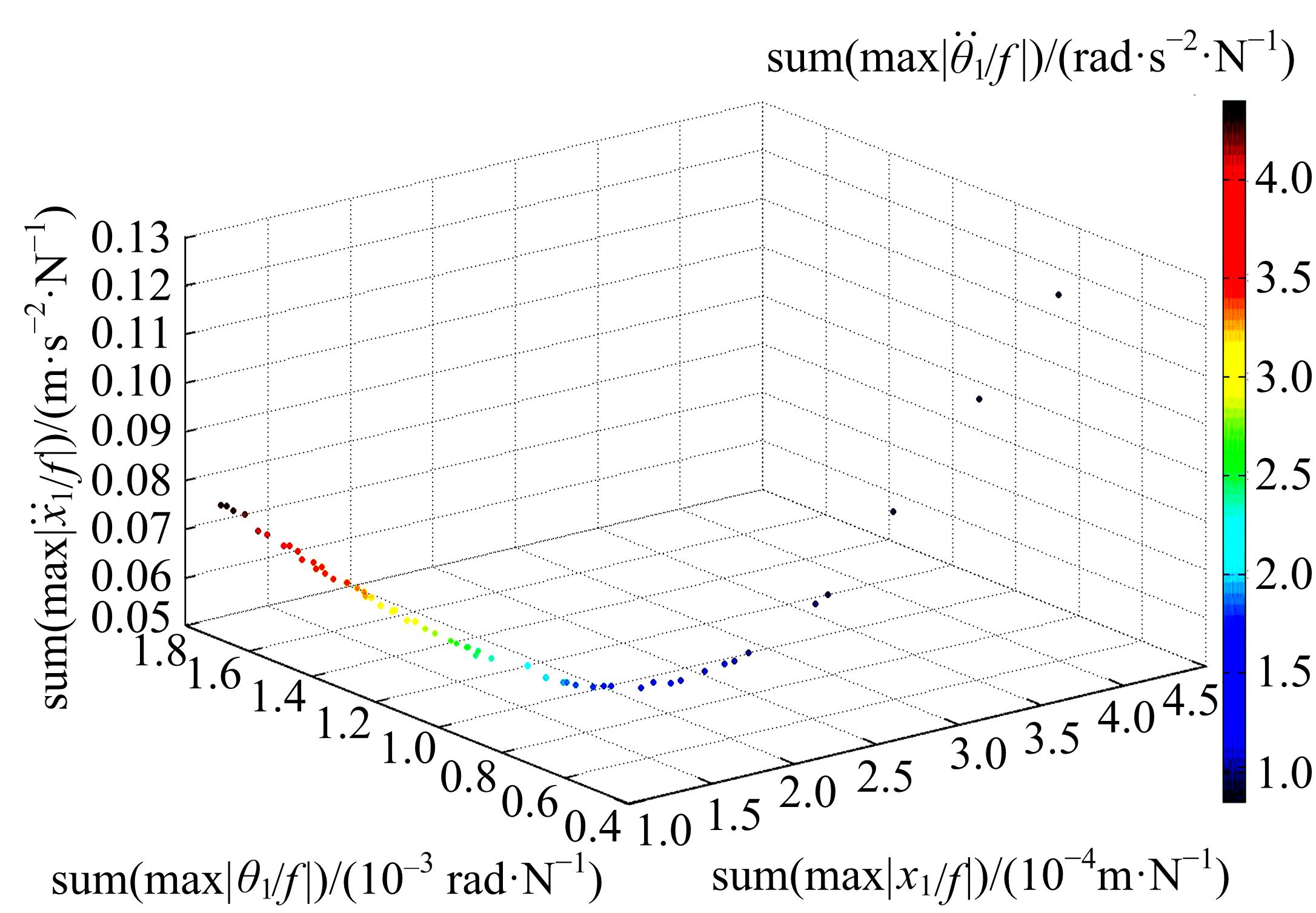
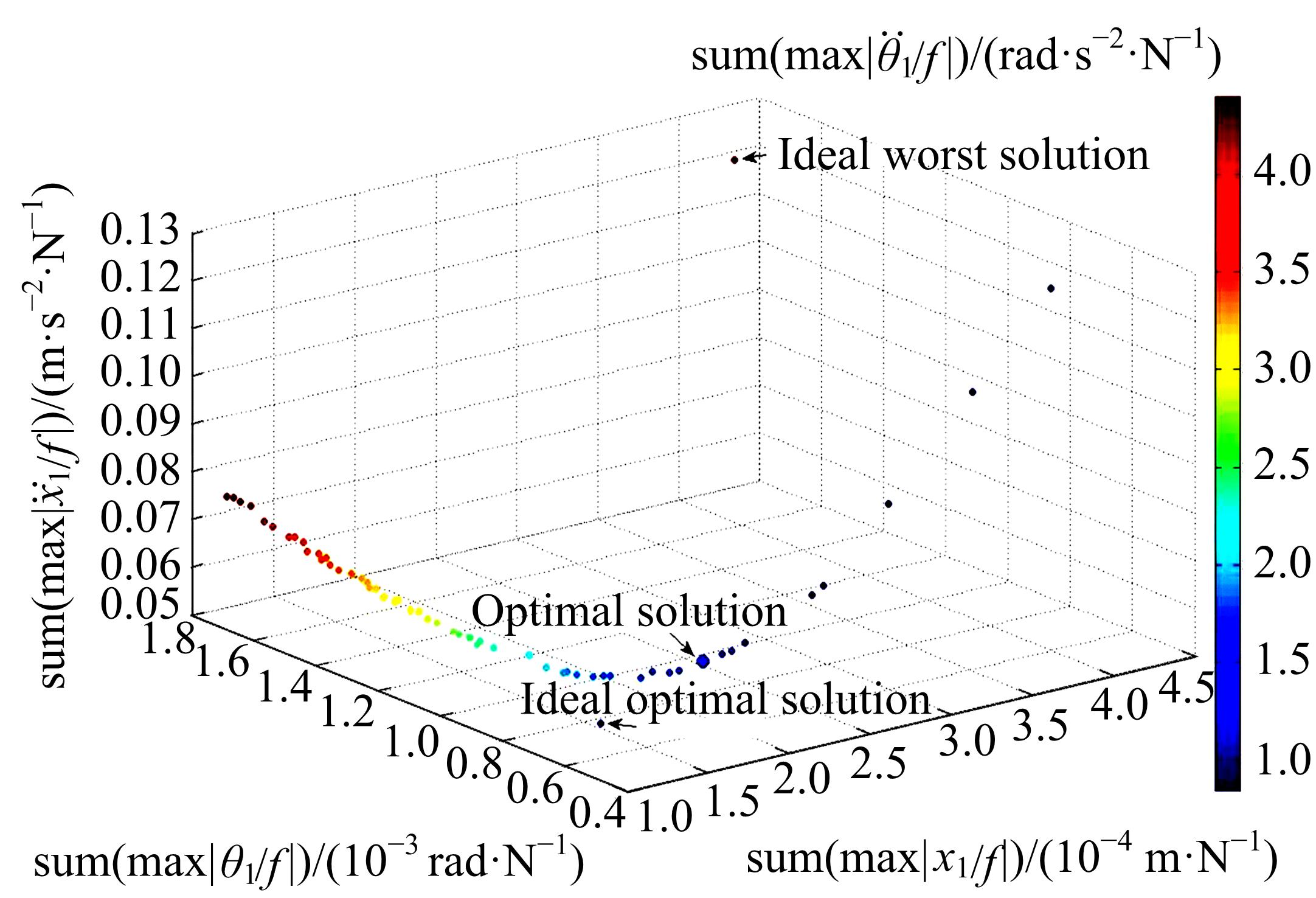
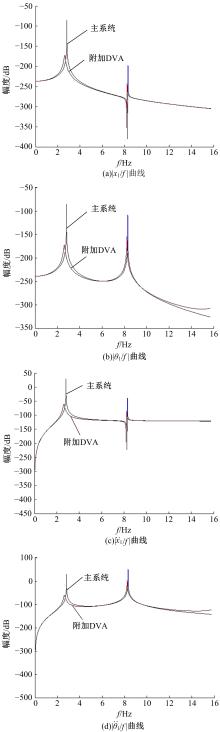
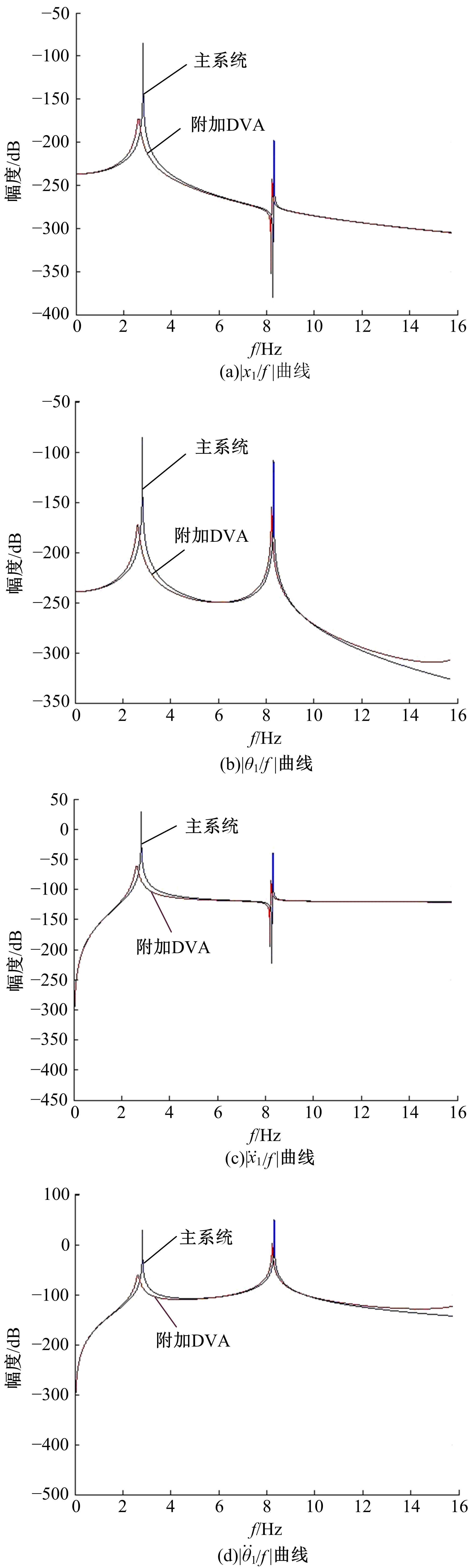
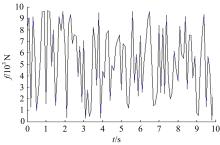
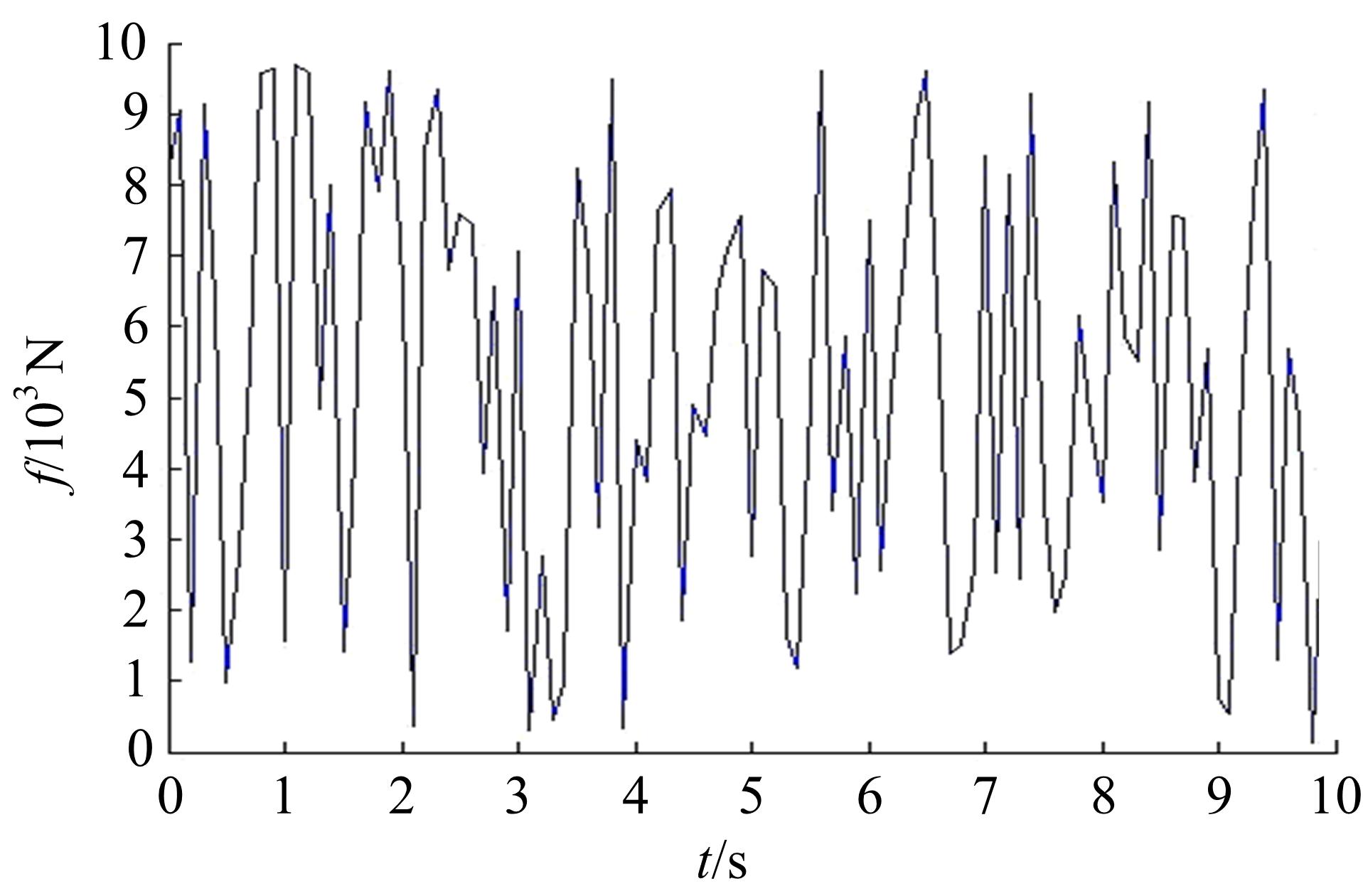
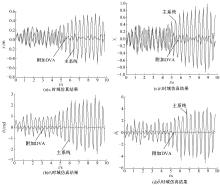
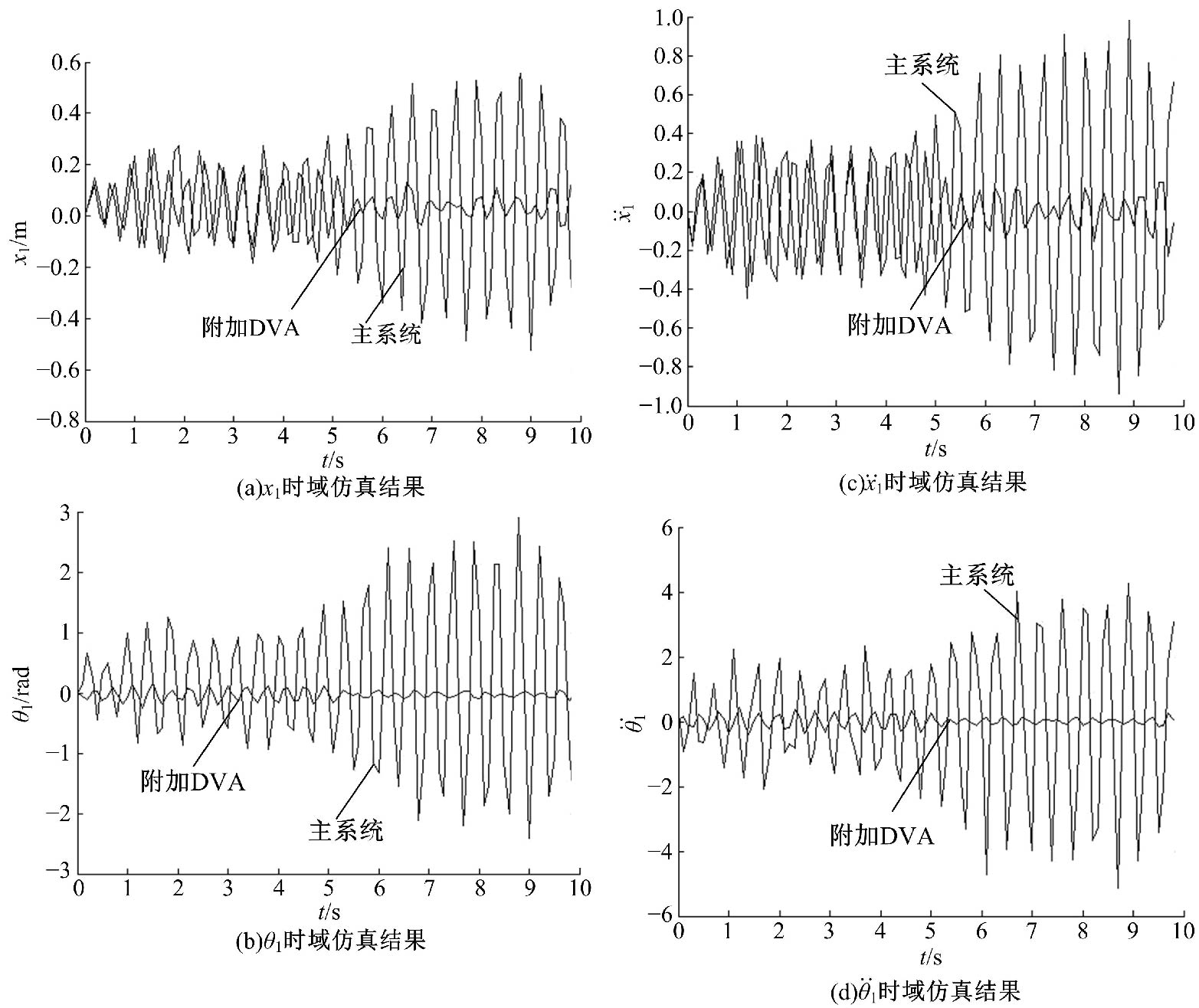
针对实际工况中常见的具有平移和绕质心转动两个自由度的无阻尼主系统，提出了一种二自由度动力吸振器，通过对吸振器刚度和阻尼的优化，使主系统获得良好的减振效果。用位移、加速度、角位移和角加速度对主系统振动进行评价并作为优化目标。采用带精英策略的非支配排序遗传算法（NSGA-Ⅱ）解决4个优化目标、3个设计变量的多目标优化问题，得到含有60个解的Pareto最优解集。用熵权TOPSIS法对Pareto最优解进行排序，选取最优解作为动力吸振器优化设计的解。对动力吸振器进行仿真分析，频域仿真结果和随机激励下的时域仿真结果表明：参数优化后的动力吸振器使得主系统的4个振动评价指标均大幅降低，二自由度动力吸振器的振动控制效果良好，NSGA-Ⅱ和熵权TOPSIS联合优化方法适用于二自由度动力吸振器的优化设计。

关键词: 机械设计, 二自由度动力吸振器, 多目标优化, 遗传算法, 多属性决策

Abstract:

This paper presents a 2-DOF dynamic vibration absorber to reduce the vibration of 2-DOF main system which possesses translation and rotation around the centroiding. The main system obtains a good damping effect by optimizing the stiffness and damping of the dynamic vibration absorber. The evaluation and optimization indexes are displacement, acceleration, angular displacement and angular acceleration. The nondominated sorting genetic algorithm (NSGA-Ⅱ) is used to solve the multi-objective optimization problem including four optimization objectives and three design variables. The 60 Pareto optimal solutions are ordered by entropy weight TOPSIS. The optimal solution is selected as the dynamic vibration absorber optimization design solution and a simulation analysis is carried out to obtain the frequency domain simulation results and time domain simulation results. The results show that the dynamic vibration absorber with optimized parameters greatly reduce the four vibration evaluation indexes of the main system and the vibration control effect of the two-DOF dynamic vibration absorber is good. The NSGA-Ⅱ and Entropy TOPSIS joint optimization method is suitable for optimal design of two-DOF dynamic vibration absorber.

Key words: mechanical design, two-DOF dynamic vibration absorber, multi-objective optimization, genetic algorithm, multi-attribute decision making

中图分类号:

TH113.1

贾富淳,孟宪皆,雷雨龙. 基于多目标遗传算法的二自由度动力吸振器优化设计[J]. 吉林大学学报(工学版), 2019, 49(6): 1969-1976.

Fu-chun JIA,Xian-jie MENG,Yu-long LEI. Optimal design of two degrees of freedom dynamic vibration absorber based on multi-objective genetic algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(6): 1969-1976.

图/表 9

图1

图2

图3

表1

决策结果"

序数	方案
序数	1	2	3	4	5
sum(max\|x ₁/f\|)/（10^-4 m·N^-1）	1.88	1.78	1.96	2	1.74
sum(max\|θ ₁/f\|)/（10^-4 rad·N^-1）	6.17	6.43	5.98	5.87	6.55
sum(max\| $x ¨$ ₁/f\|)/（10^-2 m·s^-2·N^-1）	6.43	6.25	6.58	6.64	6.2
sum(max\| $θ ¨ 1$ /f \|)/（rad·s^-2·N^-1）	1.217	1.31	1.146	1.107	1.35
k ₃/(10⁴ N·m^-1)	2.865	2.47	3.074	3.335	2.387
k ₄/(10⁴ N·m^-1)	1.019	1.015	1.019	1.015	1.014
c/(10³ N·s·m^-1)	1.296	1.291	1.443	1.438	1.241
综合评价指数方正汇总行C	0.153	0.154	0.155	0.156	0.162

表1

图4

图5

表2

幅频特性峰值"

幅频特性	峰	幅频特性峰值/dB
幅频特性	峰	主系统	附加DVA	降幅
max\|x ₁/f \|	1	-85.5	-172.1	86.6
max\|x ₁/f \|	2	-197.7	-242.1	45
max\|θ ₁/f \|	1	-85.4	-107.9	22
max\|θ ₁/f \|	2	-154.7	-172.3	17.6
max\| $x ¨$ ₁/f \|	1	29.42	-59.9	88.9
max\| $x ¨$ ₁/f \|	2	-39.50	-84.7	45.2
max\| $θ ¨ 1$ /f \|	1	29.5	-60.2	89.7
max\| $θ ¨ 1$ /f \|	2	50.2	3.1	46.9

表2

图6

图7

参考文献

1	Ormondroyd J , Denhartog P . The theory of the dynamic vibration absorber[J]. ASME Journal of Applied Mechanics, 1928, 50: 9-12.
2	Hahnkamm E . Die dampfung von fundament schwingungen bei veranderlicher erregergergrequenz[J]. Lng Arch, 1932, 4:192-201.
3	Brock J E . A note on the damped vibration absorber[J]. ASME Journal of Applied Mechanical, 1946, 68:A-284.
4	Nishimura H , Yoshida K , Shimogo T . Optimal dynamic vibration absorber for multi-degree-of-freedom systems: theoretical considerations in the case of random input[J]. JSME International Journal, 1989, 32(3): 373-379.
5	Febbo M , Vera S A . Optimization of a two degree of freedom system acting as a dynamic vibration absorber[J]. Journal of Vibration and Acoustics, 2008, 130(1): 83-88.
6	Iba D , Sone A , Masuda A . Design of multi-degree-of-freedom dynamic absorber based on bilinear matrix inequalities[J]. Transactions of the Japan Society of Mechanical Engineer, 2004, 70(695): 1929-1936.
7	Esen I , Koc M A . Optimization of a passive vibration absorber for a barrel using the genetic algorithm[J]. Expert Systems with Applications, 2015, 42(2): 894-905.
8	丁文镜 . 多自由度系振动系统动力调谐消振理论[J]. 清华大学学报, 1985, 25(3): 38-47.
8	Ding Wen-jing . Theory of dynamic tuned absorber for multidegree of freedom systems[J]. Journal of Tsinghua University，1985, 25(3): 38-47.
9	伍良生, 顾仲权, 张阿舟 . 具有多个主振模态振动系统的减振优化设计[J]. 振动工程学报, 1990, 3(4): 18-24.
9	Wu Liang-sheng , Gu Zhong-quan , Zhang A-zhou . Optimal design of vibration reduction for vibration system with sever main modes of vibration[J]. Journal of Vibration Engineering, 1990, 3(4):18-24.
10	王明武，卢旺民 . 线性多自由度系统中动力吸振器的优化研究[J].噪声与振动控制，1996，16(6): 13-16.
10	Wang Ming-wu , Lu Wang-min . Numerical fitting of optimization parameters for dynamic absorber in linear multiple degree of freedom system[J]. Noise and Vibration Control, 1996, 16(6): 13-16.
11	王全娟, 陈家义, 李伟华, 等 . 动力吸振器优化设计的功率流控制策略[J]. 振动工程学报, 2001, 14(4): 65-69.
11	Wang Quan-juan , Chen Jia-yi , Li Wei-hua , et al . Control strategies of optimum design of vibration absorber on power flow[J]. Journal of Vibration Engineering, 2001, 14(4): 65-69.
12	李俊, 金咸定, 刘见华 . 多自由度无阻尼动力吸振器的理论研究[J]. 振动、测试与诊断，2003，23(2): 23-25.
12	Li Jun , Jin Xian-ding , Liu Jian-hua . Theoretical research on undamped vibration absorber with multidegrees of freedom[J]. Journal of Vibration Measurement and Diagnosis, 2003, 23(2): 23-25.
13	侯祥林, 李和玉, 刘杰 . 最大值最小化问题的优化算法与多自由度动力减振器参数计算[J]. 振动与冲击, 2008, 27(1): 100-104.
13	Hou Xiang-lin , Li He-yu , Liu Jie . Optimal algorithm for minimization of maximum value problems and application of dynamic absorber with multi-DOF[J]. Journal of Vibration and Shock, 2008, 27(1): 100-104.
14	韩保红, 马英忱, 段云龙 . 基于遗传算法的动力吸振器参数的优化设计[J]. 价值工程, 2012, 31(9): 154-156.
14	Han Bao-hong , Ma Ying-chen , Duan Yun-long . Optimal design of parameter for dynamic vibration absorber absorber based on AMEsim[J]. Value Engineer, 2012, 31(9): 154-156.
15	王淳, 陈雅鞠 . 基于多目标粒子群算法的动力吸振器参数优化和决策研究[J]. 舰船科学技术, 2009, 31(11): 46-50.
15	Wang Chun , Chen Ya-ju . Multi-objective particle optimization and multi-attribute decision making study of dynamic vibration absorber[J]. Ship Science and Technology, 2009, 31(11): 46-50.
16	汤可宗, 杨静宇, 高尚, 等 . 一种改进的求解多目标优化问题的进化算法[J]. 南京理工大学学报, 2010, 34(4): 464-469.
16	Tang Ke-zong , Yang Jing-yu , Gao Shang , et al . Improved evolutionary algorithm for multi-objective optimization problem[J]. Journal of Nanjing University of Science and Technology, 2010, 34(4): 464-469.
17	王雷, 蔡劲草, 石鑫 . 基于改进遗传算法的多目标柔性作业车间节能调度问题[J]. 南京理工大学学报, 2017, 41(4): 494-502.
17	Wang Lei , Cai Jin-cao , Shi Xin . Multi-objective flexible job shop energy-saving scheduling problem based on improved genetic algorithm[J]. Journal of Nanjing University of Science and Technology, 2017, 41(4): 494-502.
18	Jain H , Deb K . An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach[J]. IEEE Transactions on Evolutionary Computer, 2014, 18(4): 577-601.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

[1]	谢志江,王昆,皮阳军,吴小勇,郭映位. 新的6⁃PSS型并联机构正向运动学求解方法[J]. 吉林大学学报(工学版), 2019, 49(6): 1977-1985.
[2]	曹恩国,刘坤,吉硕,孙震源,徐洪伟,骆星吉. 减重站起康复训练系统机械结构设计与优化[J]. 吉林大学学报(工学版), 2019, 49(5): 1558-1566.
[3]	李俊烨,刘洋,卢慧,孟文卿,杨兆军,张心明. 基于分子动力学的磨粒微切削单晶铁数值分析[J]. 吉林大学学报(工学版), 2019, 49(5): 1567-1574.
[4]	马芳武,韩露,周阳,王世英,蒲永锋. 采用聚乳酸复合材料的汽车零件多材料优化设计[J]. 吉林大学学报(工学版), 2019, 49(5): 1385-1391.
[5]	王宏志,姜方达,周明月. 基于遗传粒子群优化算法的认知无线电系统功率分配[J]. 吉林大学学报(工学版), 2019, 49(4): 1363-1368.
[6]	王家序,蒋倩倩,李俊阳,韩彦峰,张雷,唐挺. 双圆弧谐波传动柔轮齿形参数多目标优化设计[J]. 吉林大学学报(工学版), 2019, 49(4): 1194-1202.
[7]	张艳芹,冯雅楠,孔鹏睿,于晓东,孔祥滨. 基于热油携带的静压支承油膜温度场及试验[J]. 吉林大学学报(工学版), 2019, 49(4): 1203-1211.
[8]	杨成,赵永胜,刘志峰,蔡力钢. 基于多尺度理论的栓接结合部动力学建模[J]. 吉林大学学报(工学版), 2019, 49(4): 1212-1220.
[9]	李欣,王丹,陈军绪,孙延朋,谷诤巍,徐虹. 手刹固定板冲压成形数值模拟[J]. 吉林大学学报(工学版), 2019, 49(4): 1258-1265.
[10]	刘坤,吉硕,孙震源,徐洪伟,刘勇,赵静霞. 多功能坐站辅助型如厕轮椅机械结构设计与优化[J]. 吉林大学学报(工学版), 2019, 49(3): 872-880.
[11]	王兴野,张进秋,李国强,彭志召. 惯性质量对齿轮齿条式作动器阻尼特性的影响[J]. 吉林大学学报(工学版), 2019, 49(3): 881-887.
[12]	王家序,倪小康,韩彦峰,向果,肖科. 轴向往复运动下微槽轴承混合润滑数值模型[J]. 吉林大学学报(工学版), 2019, 49(3): 888-896.
[13]	毕秋实,王国强,黄婷婷,毛瑞,鲁艳鹏. 基于DEM-FEM耦合的双齿辊破碎机辊齿强度分析[J]. 吉林大学学报(工学版), 2018, 48(6): 1770-1776.
[14]	朱伟,王传伟,顾开荣,沈惠平,许可,汪源. 一种新型张拉整体并联机构刚度及动力学分析[J]. 吉林大学学报(工学版), 2018, 48(6): 1777-1786.
[15]	吴蔚楠,崔乃刚,郭继峰,赵杨杨. 多异构无人机任务规划的分布式一体化求解方法[J]. 吉林大学学报(工学版), 2018, 48(6): 1827-1837.