基于张量分解理论的车道级交通流数据修复算法

doi:10.13229/j.cnki.jdxbgxb20200535

吉林大学学报(工学版) ›› 2021, Vol. 51 ›› Issue (5): 1708-1715.doi: 10.13229/j.cnki.jdxbgxb20200535

• 交通运输工程·土木工程 • 上一篇

基于张量分解理论的车道级交通流数据修复算法

陆文琦¹(),周天²,谷远利²,芮一康¹(),冉斌¹

^1.东南大学交通学院，南京 211189
^2.北京交通大学综合交通运输大数据应用技术行业重点实验室，北京 100044

收稿日期:2020-07-16 出版日期:2021-09-01 发布日期:2021-09-16
通讯作者: 芮一康 E-mail:lplwq93@126.com;101012189@seu.edu.cn
作者简介:陆文琦（1993-），男，博士研究生.研究方向：交通流理论，智能网联交通.E-mail：lplwq93@126.com
基金资助:
国家自然科学基金项目(41971342);国家重点研发计划项目(2019YFB1600100);中央高校基本科研业务费专项资金项目(2242021Y10322);东南大学优秀博士学位论文培育基金项目(YBPY2161)

Data imputation approach for lane⁃scale traffic flow based on tensor decomposition theory

Wen-qi LU¹(),Tian ZHOU²,Yuan-li GU²,Yi-kang RUI¹(),Bin RAN¹

^1.School of Transportation，Southeast University，Nanjing 211189，China
^2.Key Laboratory of Transport Industry of Big Data Application Technologies for Comprehensive Transport，Ministry of Transport，Beijing Jiaotong University，Beijing 100044，China

Received:2020-07-16 Online:2021-09-01 Published:2021-09-16
Contact: Yi-kang RUI E-mail:lplwq93@126.com;101012189@seu.edu.cn

摘要/Abstract

摘要：

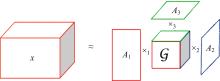
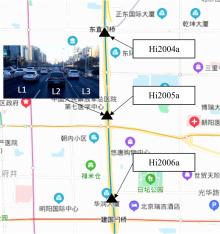
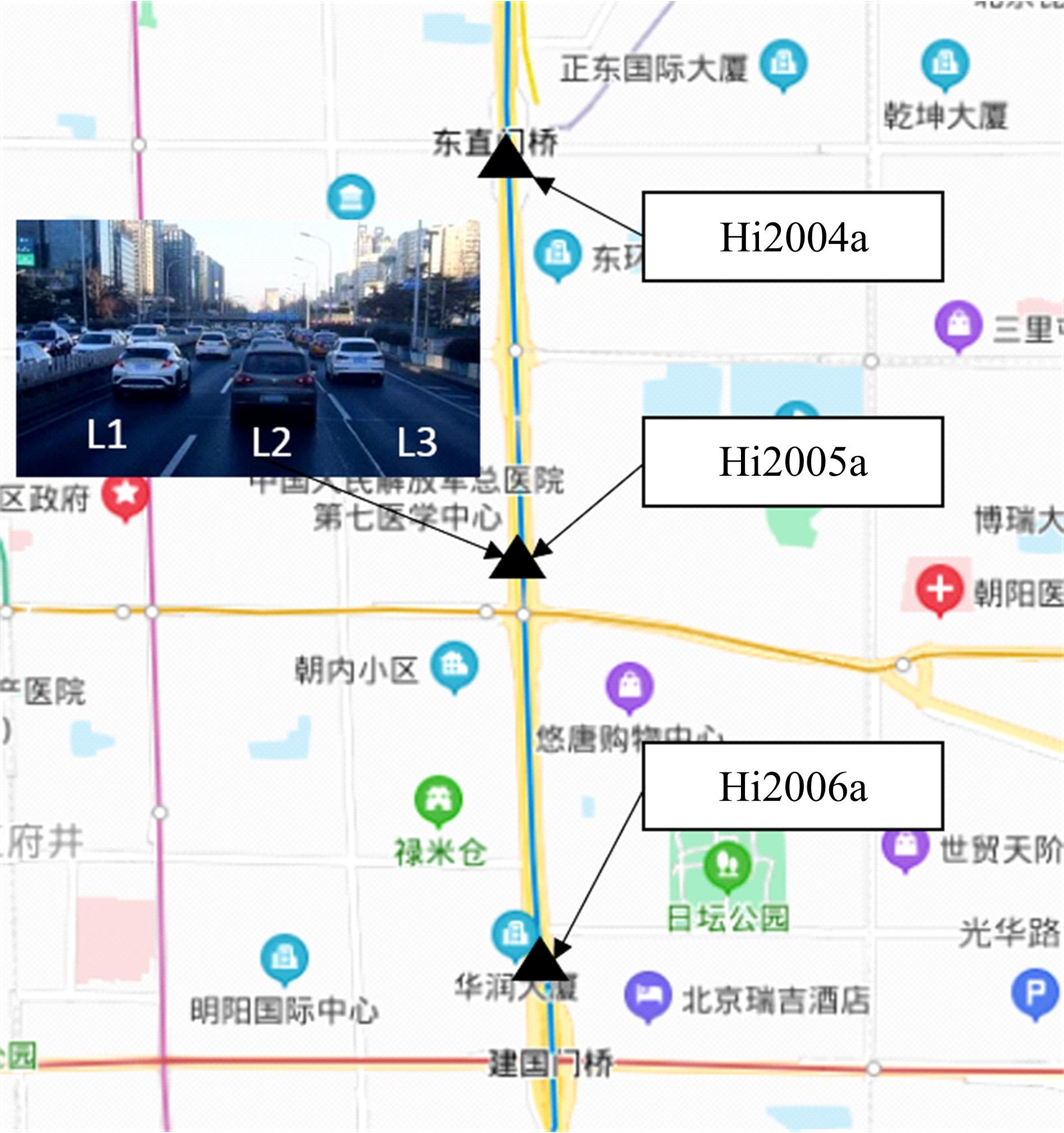
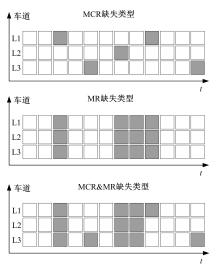
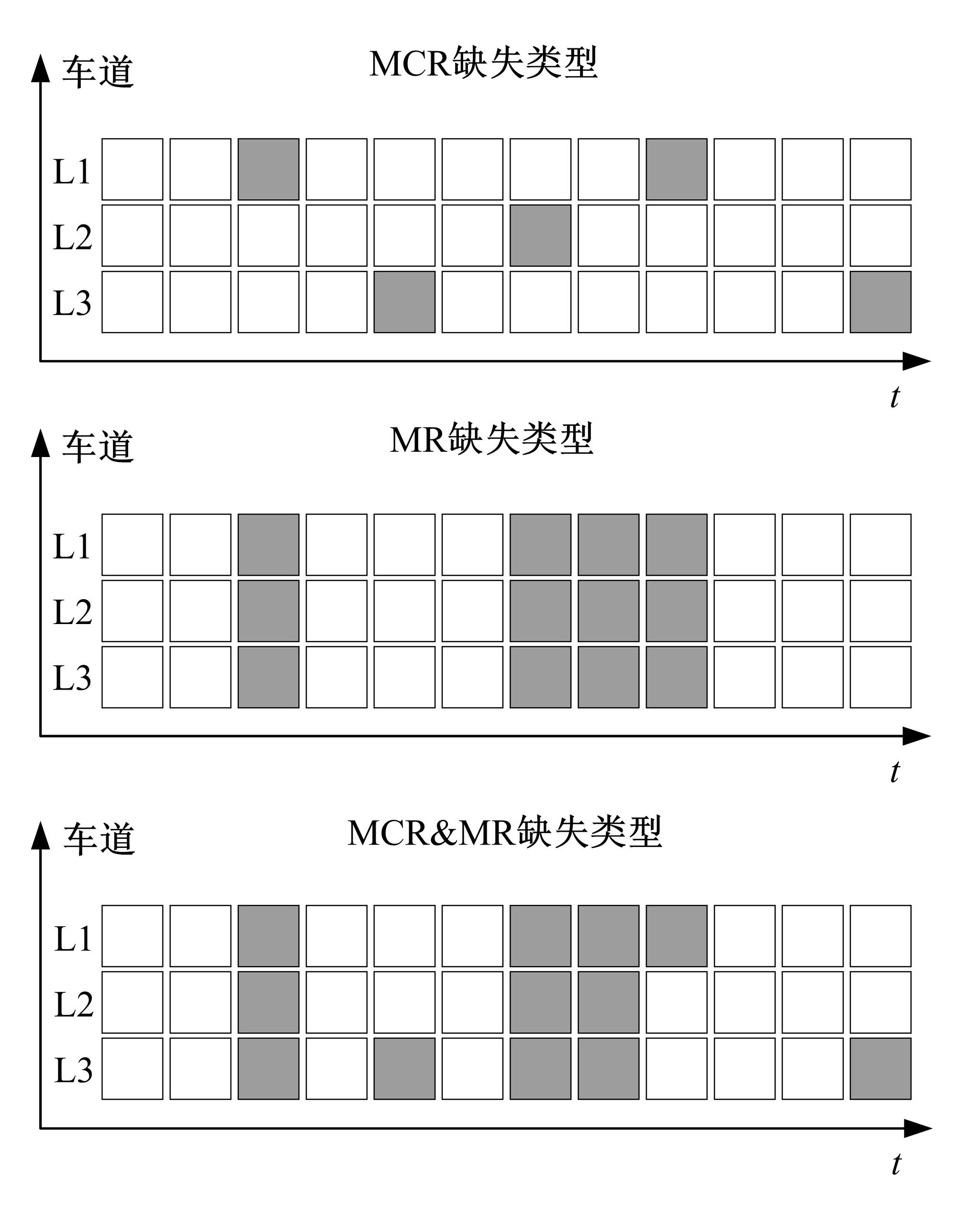
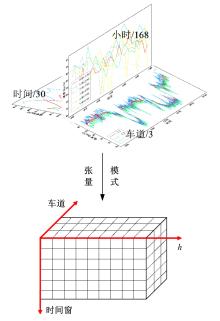
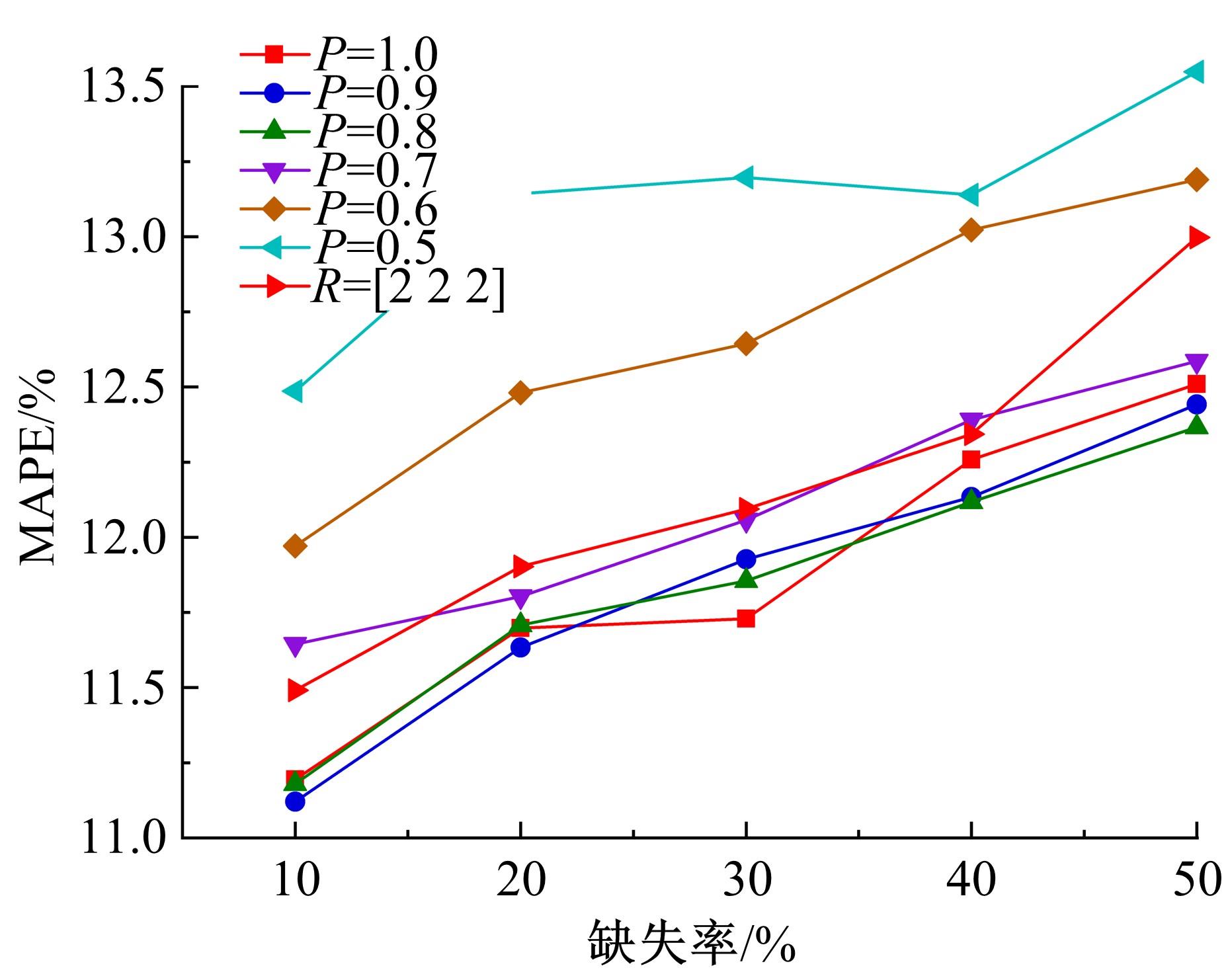
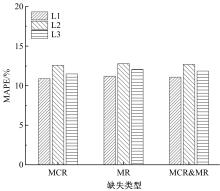
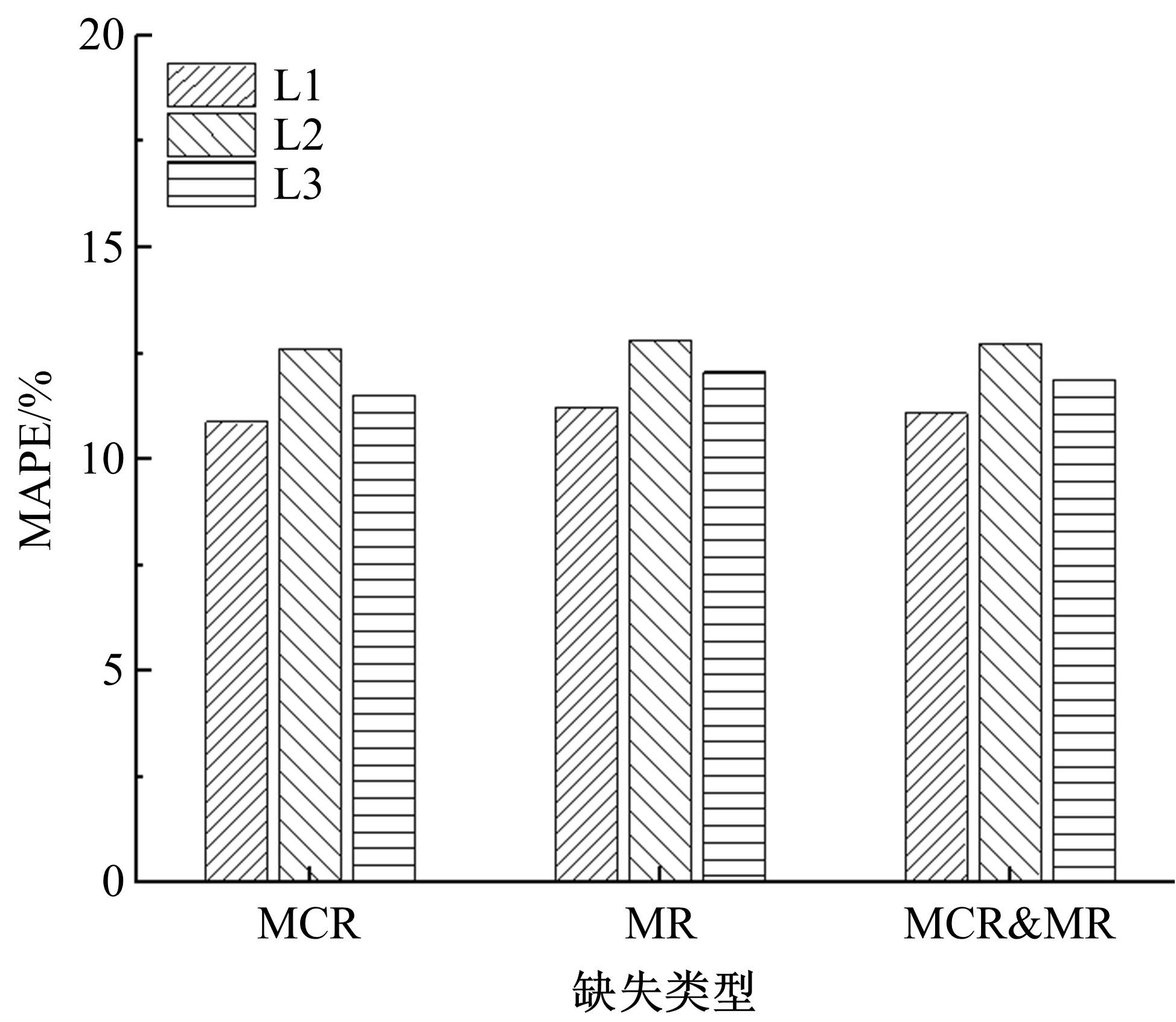
为减少数据缺失对交通流量预测、高级驾驶辅助、交通状态估计等应用的影响，提升交通流数据质量，提出一种基于自适应秩Tucker分解的插补方法（ARTDI）用于多车道交通流数据修复。将多车道交通流数据表征为张量模式，以充分利用交通流时空特性。通过张量Tucker分解构建修复目标函数，并利用动量梯度下降法求解。本文采用北京快速路多断面车道交通流速度数据构建完全随机缺失、随机缺失、混合缺失3种缺失模式进行算法验证，实验结果显示，ARTDI算法在3种缺失类型下对3个断面数据修复的平均绝对百分误差（MAPE）分别为11.67%、12.03%、11.89%。此外，随着数据缺失率的增长，ARTDI模型在不同缺失模式下的修复精度均优于对比模型，并且修复误差无显著增长，体现出ARTDI模型良好的稳定性和适用性。

关键词: 交通运输系统工程, 数据修复, 张量分解理论, Tucker分解, 车道交通流

Abstract:

To reduce the impact of the missing traffic data on traffic flow prediction， advanced driving assistance， traffic state estimation， and other traffic applications， an adaptive rank Tucker decomposition-based imputation approach （ARTDI） is proposed to recover the missing data and improve the data quality. Multi-lane traffic flow data are represented as a tensor to make full use of the spatial-temporal characteristics of traffic flow. The objective function of the imputation approach is determined through Tucker decomposition and solved by the momentum gradient descent method. Three missing types of traffic datasets including the completely random missing， random missing， and mixed missing were constructed based on the lane-scale traffic speed data of the multiple road sections of the expressway in Beijing. The experimental results indicate that the mean absolute percentage errors （MAPE） of the ARTDI approach are 11.67%， 12.03%， and 11.89% respectively under the three missing types. Besides， the results demonstrate that with the increase of the missing rate， the ARTDI approach outperforms the benchmark approaches in terms of recovery accuracy under different missing types and the MAPEs of the ARTDI approach does not increase significantly. Hence， the ARTDI approach is stable and applicable.

Key words: traffic system engineering, data imputation, tensor decomposition theory, Tucker decomposition, lane-scale traffic flow

中图分类号:

U491

陆文琦,周天,谷远利,芮一康,冉斌. 基于张量分解理论的车道级交通流数据修复算法[J]. 吉林大学学报(工学版), 2021, 51(5): 1708-1715.

Wen-qi LU,Tian ZHOU,Yuan-li GU,Yi-kang RUI,Bin RAN. Data imputation approach for lane⁃scale traffic flow based on tensor decomposition theory[J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(5): 1708-1715.

图/表 11

图1

图2

图3

图4

表1

图5

表2

表3

表4

图6

表5

参考文献 21

1	Raza A, Zhong M. Hybrid artificial neural network and locally weighted regression models for lane-based short-term urban traffic flow forecasting[J]. Transportation Planning and Technology, 2018, 41(8): 901-917.
2	Gu Y L, Lu W Q, Qin L Q, et al. Short-term prediction of lane-level traffic speeds: a fusion deep learning model[J]. Transportation Research Part C: Emerging Technologies, 2019, 106: 1-16.
3	Lu W Q, Rui Y K, Yi Z W, et al. A hybrid model for lane-level traffic flow forecasting based on complete ensemble empirical mode decomposition and extreme gradient boosting[J]. IEEE Access, 2020, 8: 42042-42054.
4	Zhong M, Sharma S, Lingras P. Genetically designed models for accurate imputation of missing traffic counts[J]. Transportation Research Record, 2004(1879): 71-79.
5	Williams B M, Hoel L A. Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process: Theoretical basis and empirical results[J]. Journal of Transportation Engineering, 2003, 129(6): 664-672.
6	Bermúdez J D, Corberán-Vallet A, Vercher E. Forecasting time series with missing data using Holt's model[J]. Journal of Statistical Planning & Inference, 2009, 139(8): 2791-2799.
7	王新颖, 隽志才, 吴庆妍, 等. KNN算法的数据优化策略[J]. 吉林大学学报: 信息科学版, 2010, 28(3): 309-313.
	Wang Xin-ying, Zhi-cai Juan, Wu Qing-yan, et al. Data optimization strategy of KNN algorithm[J]. Journal of Jilin University(Information Science Edition), 2010, 28(3): 309-313.
8	陈亮, 王金泓, 何涛, 等. 基于SVR的区域交通碳排放预测研究[J]. 交通运输系统工程与信息, 2018, 18(2): 13-19.
	Chen Liang, Wang Jing-hong, He Tao, et al. Forecast study of regional transportation carbon emissions based on SVR[J]. Journal of Transportation Systems Engineering and Information Technology, 2018, 18(2): 13-19.
9	Qu L, Zhang Y, Hu J M, et al. A BPCA based missing value imputing method for traffic flow volume data[J]. IEEE Intelligent Vehicles Symposium, 2008: 985-990.
10	Qu L, Li L, Zhang Y, et al. PPCA-based missing data imputation for traffic flow volume: a systematical approach[J]. IEEE Transactions on Intelligent Transportation Systems, 2009, 10(3): 512-522.
11	Acar E, Dunlavy D M, Kolda T G, et al. Scalable tensor factorizations for incomplete data[J]. Chemometrics and Intelligent Laboratory Systems, 2011, 106(1): 41-56.
12	Tan H C, Feng G D, Feng J S, et al. A tensor-based method for missing traffic data completion[J]. Transportation Research Part C: Emerging Technologies, 2013, 28: 15-27.
13	Kolda T G, Bader B W. Tensor decompositions and applications[J]. SIAM review, 2009, 51(3): 455-500.
14	de Lathauwer L, de Moor B, Vandewalle J. A Multilinear singular value decomposition[J]. SIAM Journal on Matrix Analysis and Applications, 2000, 21(4):1253-1278.
15	Chen X Y, He Z C, Wang J W. Spatial-temporal traffic speed patterns discovery and incomplete data recovery via SVD-combined tensor decomposition[J]. Transportation Research Part C: Emerging Technologies, 2018, 86: 59-77.
16	Polyak B T. Some methods of speeding up the convergence of iteration methods[J]. USSR Computational Mathematics and Mathematical Physics, 1964, 4(5): 1-17.
17	Li L C, Du B W, Wang Y G, et al. Estimation of missing values in heterogeneous traffic data: application of multimodal deep learning model[J]. Knowledge-Based Systems, 2020, 194: 105592.
18	Chen X Y, He Z C, Sun L J. A bayesian tensor decomposition approach for spatiotemporal traffic data imputation[J]. Transportation Research Part C: Emerging Technologies, 2018, 98: 73-84.
19	谷远利, 张源, 芮小平, 等. 基于免疫算法优化LSSVM的短时交通流预测[J]. 吉林大学学报: 工学版, 2019, 49(6): 1852-1857.
	Gu Yuan-li, Zhang Yuan, Rui Xiao-ping, et al. Short-term traffic flow prediction based on LSSVM optimized by immune algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(6): 1852-1857.
20	杨飞, 方滨兴, 王春露, 等. 基于小波和回声状态网络的交通流多步预测模型[J]. 吉林大学学报: 工学版, 2013, 43(3): 646-653.
	Yang Fei, Fang Bin-xing, Wang Chun-lu, et al. Multi-step traffic flow prediction model based on wavelet and echo state network[J]. Journal of Jilin University(Engineering and Technology Edition), 2013, 43(3): 646-653.
21	龚勃文, 林赐云, 李静, 等. 基于核自组织映射-前馈神经网络的交通流短时预测[J]. 吉林大学学报: 工学版, 2011, 41(4): 938-943.
	Gong Bo-wen, Lin Xi-yun, Li Jing, et al. Short-term traffic flow prediction based on KSOM BP neural network[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(4): 938-943.

相关文章 15

[1]	卢凯,吴蔚,林观荣,田鑫,徐建闽. 基于KNN回归的客运枢纽聚集人数组合预测方法[J]. 吉林大学学报(工学版), 2021, 51(4): 1241-1250.
[2]	彭博,张媛媛,王玉婷,唐聚,谢济铭. 基于自动编码机-分类器的视频交通状态自动识别[J]. 吉林大学学报(工学版), 2021, 51(3): 886-892.
[3]	张健,吴坤润,杨敏,冉斌. 智能网联环境下交叉口双环自适应控制模型[J]. 吉林大学学报(工学版), 2021, 51(2): 541-548.
[4]	王殿海,沈辛夷,罗小芹,金盛. 车均延误最小情况下的相位差优化方法[J]. 吉林大学学报(工学版), 2021, 51(2): 511-523.
[5]	宋现敏,张明业,李振建,王鑫,张亚南. 动态公交专用道的设置及其仿真分析评价[J]. 吉林大学学报(工学版), 2020, 50(5): 1677-1686.
[6]	贾洪飞,丁心茹,杨丽丽. 城市潮汐车道优化设计的双层规划模型[J]. 吉林大学学报(工学版), 2020, 50(2): 535-542.
[7]	尹超英,邵春福,王晓全,熊志华. 考虑空间异质性的建成环境对通勤方式选择的影响[J]. 吉林大学学报(工学版), 2020, 50(2): 543-548.
[8]	张大伟,祝海涛. 考虑行人差异性的人群疏散最优决策理论模型[J]. 吉林大学学报(工学版), 2020, 50(2): 549-556.
[9]	常玉林,袁才鸿,孙超,张鹏. 基于改进元胞传输模型的城市路网实际阻抗计算方法[J]. 吉林大学学报(工学版), 2020, 50(1): 132-139.
[10]	宗长富,文龙,何磊. 基于欧几里得聚类算法的三维激光雷达障碍物检测技术[J]. 吉林大学学报(工学版), 2020, 50(1): 107-113.
[11]	隋振,姜源. 基于MIMO类脑情感学习回路的横-纵向综合控制驾驶员模型[J]. 吉林大学学报(工学版), 2020, 50(1): 140-146.
[12]	别一鸣,姜凯,汤茹茹,王琳虹,熊昕宇. 考虑方案过渡影响的单点交通控制时段划分方法[J]. 吉林大学学报(工学版), 2019, 49(6): 1844-1851.
[13]	谷远利, 张源, 芮小平, 陆文琦, 李萌, 王硕. 基于免疫算法优化LSSVM的短时交通流预测[J]. 吉林大学学报(工学版), 2019, 49(6): 1852-1857.
[14]	程国柱, 冯思鹤, 冯天军. 占用车行道的路内停车泊位设置条件[J]. 吉林大学学报(工学版), 2019, 49(6): 1858-1864.
[15]	龙海波,杨家其,赵学彧. 基于转运延误风险的多方式协同货运载运工具配置优化[J]. 吉林大学学报(工学版), 2019, 49(5): 1492-1499.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

缺失率/%	KNN	SVR	CP-WOPT	TDI	ARTDI
10	11.69	12.25	16.55	11.82	10.84
20	14.05	14.22	18.07	12.64	11.22
30	16.31	16.61	18.81	13.63	11.68
40	20.66	20.94	21.38	14.35	12.07
50	29.07	28.62	24.72	16.51	12.52
平均值	18.36	18.53	19.90	13.79	11.67

缺失率/%	KNN	SVR	CP-WOPT	TDI	ARTDI
10	12.33	11.31	16.42	14.37	11.52
20	14.54	14.75	18.03	15.62	11.59
30	16.19	15.93	20.36	17.64	12.02
40	20.40	21.82	22.10	19.05	12.38
50	28.02	31.47	27.65	21.82	12.66
平均值	18.30	19.05	20.91	17.70	12.03

缺失率/%	KNN	SVR	CP- WOPT	TDI	ARTDI
10	12.25	12.41	16.68	12.82	11.19
20	14.22	14.77	17.72	15.04	11.70
30	16.61	16.97	18.79	16.06	11.73
40	20.94	21.85	21.01	16.99	12.26
50	28.62	32.77	24.71	19.68	12.58
平均值	18.53	19.75	19.78	16.12	11.89

张量模式	MR	MCR	MR&MCR	平均值
30×24×3	19.03	17.67	18.50	18.77
30×168×3	12.03	11.67	11.89	11.96
30×168×9	16.91	15.95	16.78	16.85

基于张量分解理论的车道级交通流数据修复算法

Data imputation approach for lane⁃scale traffic flow based on tensor decomposition theory

RICH HTML

PDF (PC)

摘要/Abstract

引用本文

使用本文

图/表 11

参考文献 21

相关文章 15

Metrics

本文评价

推荐阅读 0