吉林大学学报(工学版) ›› 2019, Vol. 49 ›› Issue (4): 1092-1099.doi: 10.13229/j.cnki.jdxbgxb20180211

• • 上一篇    

基于最优速度模型的改进安全距离跟驰模型

曲昭伟1(),潘昭天1,陈永恒1(),陶鹏飞1,孙迪2   

  1. 1. 吉林大学 交通学院, 长春 130022
    2. 北京联合大学 城市轨道交通与物流学院，北京 100101
  • 收稿日期:2018-03-09 出版日期:2019-07-01 发布日期:2019-07-16
  • 通讯作者: 陈永恒 E-mail:quzw@jlu.edu.cn;cyh@jlu.edu.cn
  • 作者简介:曲昭伟(1962?)，男，教授，博士生导师. 研究方向：交通流理论，交通视频处理，交通控制.E?mail:quzw@jlu.edu.cn
  • 基金资助:
    国家自然科学基金项目(51705196);北京市教育委员会科技计划面上项目(KM201511417005)

Car⁃following model with improving safety distance based on optimal velocity model

Zhao⁃wei QU1(),Zhao⁃tian PAN1,Yong⁃heng CHEN1(),Peng⁃fei TAO1,Di SUN2   

  1. 1. College of Transportation, Jilin University, Changchun 130022, China
    2. School of Urban Rail Transit and Logisitic, Beijing Union University, Beijing 100101, China
  • Received:2018-03-09 Online:2019-07-01 Published:2019-07-16
  • Contact: Yong?heng CHEN E-mail:quzw@jlu.edu.cn;cyh@jlu.edu.cn

RICH HTML

 13   

PDF (PC)

234

摘要：

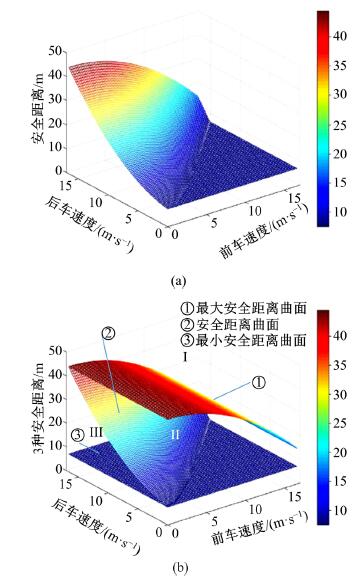
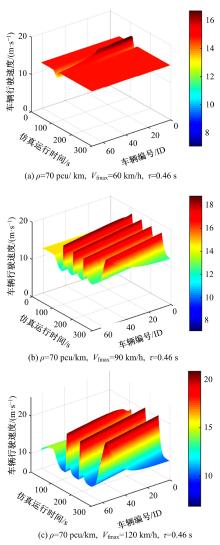
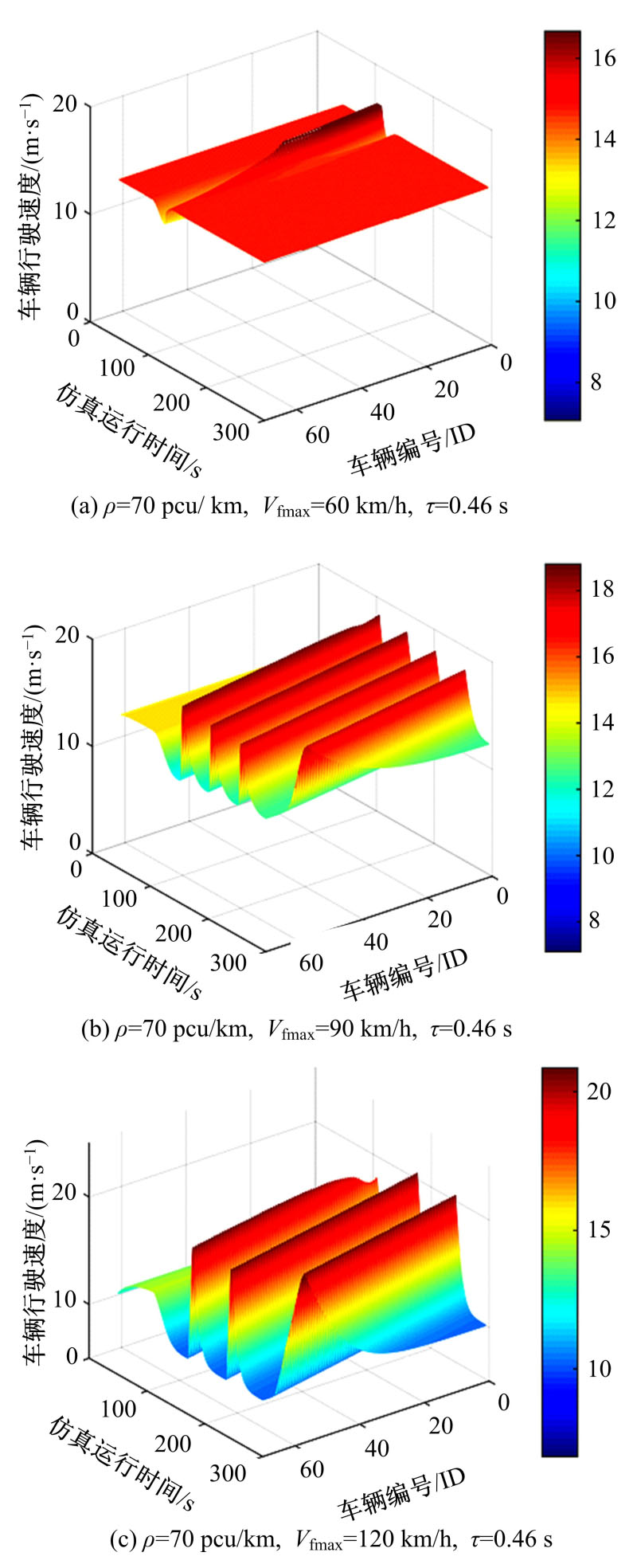
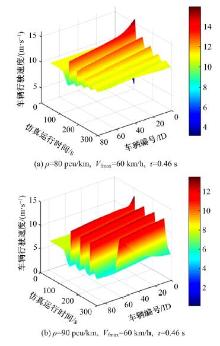
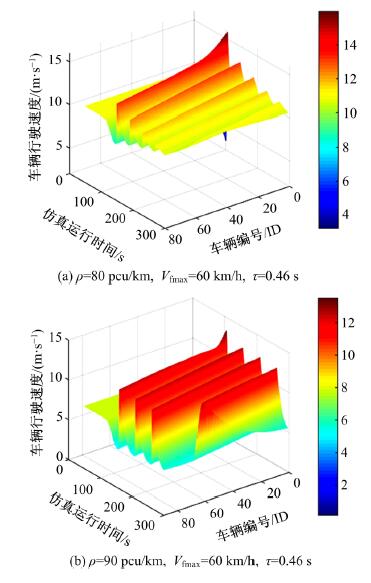
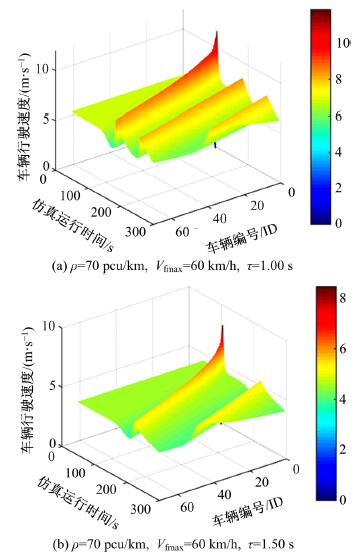
针对最优速度（OV）模型及其相关衍生模型（GF,FVD等）假设安全距离恒定的缺陷，提出了基于最优速度模型的改进安全距离跟驰模型，并对本文模型的改进情况进行理论分析。根据本文模型仿真分析了道路车流密度、车辆最大可行驶速度和驾驶员反应延迟时间对交通流稳定性的影响。最后，采用美国NGSIM数据库数据作为样本，通过聚类分析对本文模型进行检验，并与OV模型、GF模型和FVD模型进行对比，结果证明了本文模型的准确性和有效性。

关键词: 交通运输系统工程, 跟驰模型, 数值仿真, 交通流理论

Abstract:

In order to overcome the defect of fixed safety distance in Optimal Velocity (OV) model and its related derivative generalized force (GF) model and full velocity difference (FVD) model, a car-following model with improving safety distance based on the OV model is proposed in this paper. The improvements of the proposed model are analyzed theoretically. Then, according to the proposed model, the simulation frameworks are developed to analyze the impact of three model parameters on traffic flow stability. These parameters are the density of traffic flow on the road, the maximum velocity for driving vehicle and the time of driver's reaction delay. The simulation can truly reproduce the propagation state of traffic flow. Finally, using the data from U.S. NGSIM Database as samples, the accuracy and effectiveness of the model presented in this paper are verified after testing with cluster analysis by comparing with OV model, GF model and FVD model.

Key words: engineering of communications and transportation system, car?following model, numerical simulation, traffic flow theory

中图分类号: 

  • U491.25

图 1

安全距离曲面分析图"

图2

模型参数（V fmax）对道路交通流稳定性影响分析"

图3

模型参数（ρ）对道路交通流稳定性影响分析"

图4

模型参数（ τ ）对道路交通流稳定性影响分析"

表1

检验样本K?means聚类中心及各类样本数量"

类编号 MEAN VAR 类内样本数量
1 19.057 3.4068 1561
2 8.6798 78.062 167
3 8.0471 23.305 381
4 7.353 49.766 284
5 5.0778 2.9554 591

表2

各类样本均方根误差（RMSE）的均值和方差"

类编号 RMSE OV GF FVD MCF
1 MEAN 31.14 31.60 31.17 18.90
VAR 870.56 895.75 871.19 629.49
2 MEAN 39.64 39.97 39.66 33.45
VAR 2444.55 2479.77 2445.07 2255.03
3 MEAN 28.74 29.22 28.77 20.86
VAR 1418.24 1458.84 1418.55 1309.34
4 MEAN 30.36 30.80 30.39 24.37
VAR 1973.46 2047.67 1973.67 1565.88
5 MEAN 36.64 37.94 36.66 21.47
VAR 2174.57 2258.46 2175.35 1747.29
1 Bando M , Hasebe K , Nakayama A , et al . Dynamical model of traffic congestion and numerical simulation[J]. Physical Review E, 1995, 51(2): 1035⁃1042.
2 Helbing D , Tilch B . Generalized force model of traffic dynamics[J]. Physical Review E, 1998, 58(1): 133⁃138.
3 Jiang Rui , Wu Qing⁃song , Zhu Zuo⁃jin . Full velocity difference model for a car⁃following theory[J]. Physical Review E, 2001, 64(1): 17101.
4 Ge H X , Zhu H B , Dai S Q . Effect of looking backward on traffic flow in a cooperative driving car following model[J]. The European Physical Journal B, 2006, 54(4): 503⁃507.
5 王涛，高自友，赵小梅 . 多速度差模型及稳定性分析[J]. 物理学报, 2006, 55(2): 634⁃640.
Wang Tao , Gao Zi⁃you , Zhao Xiao⁃mei . Multiple velocity difference model and its stability analysis[J]. Acta Physia Sinica, 2006, 55(2): 634⁃640.
6 Bonneson J A , Pratt M P , Vandehey M A . Predicting arrival flow profiles and platoon dispersion for urban street segments[J]. Journal of the Transportation Research Board, 2010, 2173: 28⁃35.
7 葛红霞，崔煜，程荣军 . 考虑前后车效应的反馈控制跟驰模型[J]. 物理学报, 2014, 63(11): 103⁃109.
Ge Hong⁃xia , Cui Yu , Cheng Rong⁃jun . A car⁃following model with considering control signals from front and rear[J]. Acta Physia Sinica, 2014, 63(11): 103⁃109.
8 Chen J , Liu R , Ngoduy D , et al . A new multi⁃anticipative car⁃following model with consideration of the desired following distance[J]. Nonlinear Dynamics, 2016, 85(4): 2705⁃2717.
9 Peng Guang⁃han , Lu Wei⁃zhen , He Hong⁃di , et al . Nonlinear analysis of a new car⁃following model accounting for the optimal velocity changes with memory[J]. Communications in Nonlinear Science and Numerical Simulation, 2016, 40: 197⁃205.
10 杨龙海，赵顺，徐洪 . 基于改进优化速度函数的跟驰模型研究[J]. 交通运输系统工程与信息, 2017, 17(2): 41⁃46, 67.
Yang Long⁃hai , Zhao Shun , Xu Hong . Car⁃following model based on the modified optimal velocity function[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(2): 41⁃46, 67.
11 李腾龙，惠飞 . 考虑后视和最优速度记忆的跟驰模型及仿真[J]. 计算机工程与应用, 2017, 53(12): 249⁃254, 270.
Li Teng⁃long , Hui Fei . Numerical simulation of car⁃following model considering optimal velocity changes with memory and backward looking effect[J]. Computer Engineering and Applications, 2017, 53(12): 249⁃254, 270.
12 Li Zhi⁃peng , Xu Xun , Xu Shang⁃zhi , et al . A heterogeneous traffic flow model consisting of two types of vehicles with different sensitivities[J]. Communications in Nonlinear Science and Numerical Simulation, 2017, 42: 132⁃145.
13 Kuang Hua , Xu Zhi⁃Peng , Li Xing⁃Li , et al . An extended car⁃following model accounting for the average headway effect in intelligent transportation system[J]. Physica A: Statistical Mechanics and its Applications, 2017, 471: 778⁃787.
14 胡彦梅，马天山，陈建忠 . 交通流多预期延迟模型与数值仿真[J]. 计算机应用研究, 2018, 35(1): 48⁃51.
Hu Yan⁃mei , Ma Tian⁃shan , Chen Jian⁃zhong . Multi⁃anticipation delay model for traffic flow and numerical simulation[J]. Application Research of Computers, 2018, 35(1): 48⁃51.
15 Li Zhi⁃peng , Li Wen⁃zhong , Xu Shang⁃zhi , et al . Analyses of vehicle’s self⁃stabilizing effect in an extended optimal velocity model by utilizing historical velocity in an environment of intelligent transportation system[J]. Nonlinear Dynamics, 2015, 80(1/2): 529⁃540.
16 陈春燕，许志鹏，邝华 . 连续记忆效应的交通流跟驰建模与稳定性分析[J]. 广西师范大学学报:自然科学版, 2017, 35(3): 14⁃21.
Chen Chun⁃yan , Xu Zhi⁃peng , Kuang Hua . Modeling and stability analysis of traffic flow car⁃following model with continuous memory effect[J]. Journal of Guangxi Normal University (Natural Science Edition), 2017, 35(3): 14⁃21.
17 Li P Y , Shrivastava A . Traffic flow stability induced by constant time headway policy for adaptive cruise control vehicles[J]. Transportation Research Part C: Emerging Technologies, 2002, 10(4): 275⁃301.
18 秦严严，王昊，王炜, 等 . 不同CACC渗透率条件下的混合交通流稳定性分析[J]. 交通运输系统工程与信息, 2017, 17(4): 63⁃69,104.
Qin Yan⁃yan , Wang Hao , Wang Wei , et al . Mixed traffic flow string stability analysis for different CACC penetration ranges[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(4): 63⁃69,104.
[1] 白乔文,曲昭伟,陈永恒,熊帅,陶楚青. 非严格优先权下无左转专用相位直行车辆轨迹模型建立[J]. 吉林大学学报(工学版), 2019, 49(3): 673-679.
[2] 李志慧,钟涛,赵永华,胡永利,李海涛,赵景伟. 面向车辆自主驾驶的行人跟踪算法[J]. 吉林大学学报(工学版), 2019, 49(3): 680-687.
[3] 曹宁博,赵利英,曲昭伟,陈永恒,白乔文,邓晓磊. 考虑双向行人跟随行为的社会力模型[J]. 吉林大学学报(工学版), 2019, 49(3): 688-694.
[4] 罗小芹,王殿海,金盛. 面向混合交通的感应式交通信号控制方法[J]. 吉林大学学报(工学版), 2019, 49(3): 695-704.
[5] 陈磊,王江锋,谷远利,闫学东. 基于思维进化优化的多源交通数据融合算法[J]. 吉林大学学报(工学版), 2019, 49(3): 705-713.
[6] 尹超英,邵春福,王晓全. 考虑停车可用性的建成环境对小汽车通勤出行的影响[J]. 吉林大学学报(工学版), 2019, 49(3): 714-719.
[7] 凃强,程琳,林芬,孙超. 考虑出行者风险态度的最优路径搜索[J]. 吉林大学学报(工学版), 2019, 49(3): 720-726.
[8] 陈永恒,刘芳宏,曹宁博. 信控交叉口行人与提前右转机动车冲突影响因素[J]. 吉林大学学报(工学版), 2018, 48(6): 1669-1676.
[9] 常山,宋瑞,何世伟,黎浩东,殷玮川. 共享单车故障车辆回收模型[J]. 吉林大学学报(工学版), 2018, 48(6): 1677-1684.
[10] 曲大义,杨晶茹,邴其春,王五林,周警春. 基于干线车流排队特性的相位差优化模型[J]. 吉林大学学报(工学版), 2018, 48(6): 1685-1693.
[11] 宗芳, 齐厚成, 唐明, 吕建宇, 于萍. 基于GPS数据的日出行模式-出行目的识别[J]. 吉林大学学报(工学版), 2018, 48(5): 1374-1379.
[12] 刘翔宇, 杨庆芳, 隗海林. 基于随机游走算法的交通诱导小区划分方法[J]. 吉林大学学报(工学版), 2018, 48(5): 1380-1386.
[13] 钟伟, 隽志才, 孙宝凤. 不完全网络的城乡公交一体化枢纽层级选址模型[J]. 吉林大学学报(工学版), 2018, 48(5): 1387-1397.
[14] 刘兆惠, 王超, 吕文红, 管欣. 基于非线性动力学分析的车辆运行状态参数数据特征辨识[J]. 吉林大学学报(工学版), 2018, 48(5): 1405-1410.
[15] 宗芳, 路峰瑞, 唐明, 吕建宇, 吴挺. 习惯和路况对小汽车出行路径选择的影响[J]. 吉林大学学报(工学版), 2018, 48(4): 1023-1028.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
版权所有 © 《吉林大学学报(工学版)》编辑部
地址：长春市人民大街5988号　电话：+86-431-85095297　传真：+86-431-85094074　E-mail: xbgxb@jlu.edu.cn
本系统由北京玛格泰克科技发展有限公司设计开发