吉林大学学报(工学版) ›› 2021, Vol. 51 ›› Issue (1): 225-232.doi: 10.13229/j.cnki.jdxbgxb20200451

• 交通运输工程·土木工程 • 上一篇    

基于有限元方法的裂缝箱梁桥自振特性分析

孔庆雯1(),谭国金1,王龙林2(),王勇3,魏志刚4,刘寒冰1   

  1. 1.吉林大学 交通学院，长春 130022
    2.广西交科集团有限公司，南宁 530007
    3.吉林省公路管理局，长春 130021
    4.吉林省高等级公路建设局，长春 130033
  • 收稿日期:2020-05-06 出版日期:2021-01-01 发布日期:2021-01-20
  • 通讯作者: 王龙林 E-mail:kongqw18@mails.jlu.edu.cn;wangll18577888161@gmail.com
  • 作者简介:孔庆雯（1996-），女，博士研究生. 研究方向：桥梁检测与加固. E-mail: kongqw18@mails.jlu.edu.cn
  • 基金资助:
    国家自然科学基金项目(51978309);吉林省科技厅科技攻关项目(20190303052SF);吉林省交通运输厅科技项目(2020-1-3);吉林省发展改革委项目(2019C041-5);吉林省教育厅“十三五”科学技术项目(JJKH20190150KJ)

Analysis of free vibration characteristics of cracked box girder bridge based on finite element method

Qing-wen KONG1(),Guo-jin TAN1,Long-lin WANG2(),Yong WANG3,Zhi-gang WEI4,Han-bing LIU1   

  1. 1.College of Transportation，Jilin University，Changchun 130022，China
    2.Guangxi Transportation Science and Technology Group Co. ，Ltd. ，Nanning 530007，China
    3.Jilin Provincial Highway Administration，Changchun 130021，China
    4.Jilin Provincial High Class Highway Construction Bureau，Changchun 130033，China
  • Received:2020-05-06 Online:2021-01-01 Published:2021-01-20
  • Contact: Long-lin WANG E-mail:kongqw18@mails.jlu.edu.cn;wangll18577888161@gmail.com

RICH HTML

 2   

PDF (PC)

316

摘要：

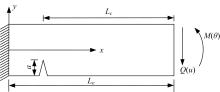
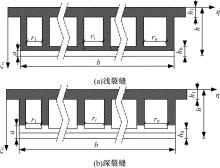
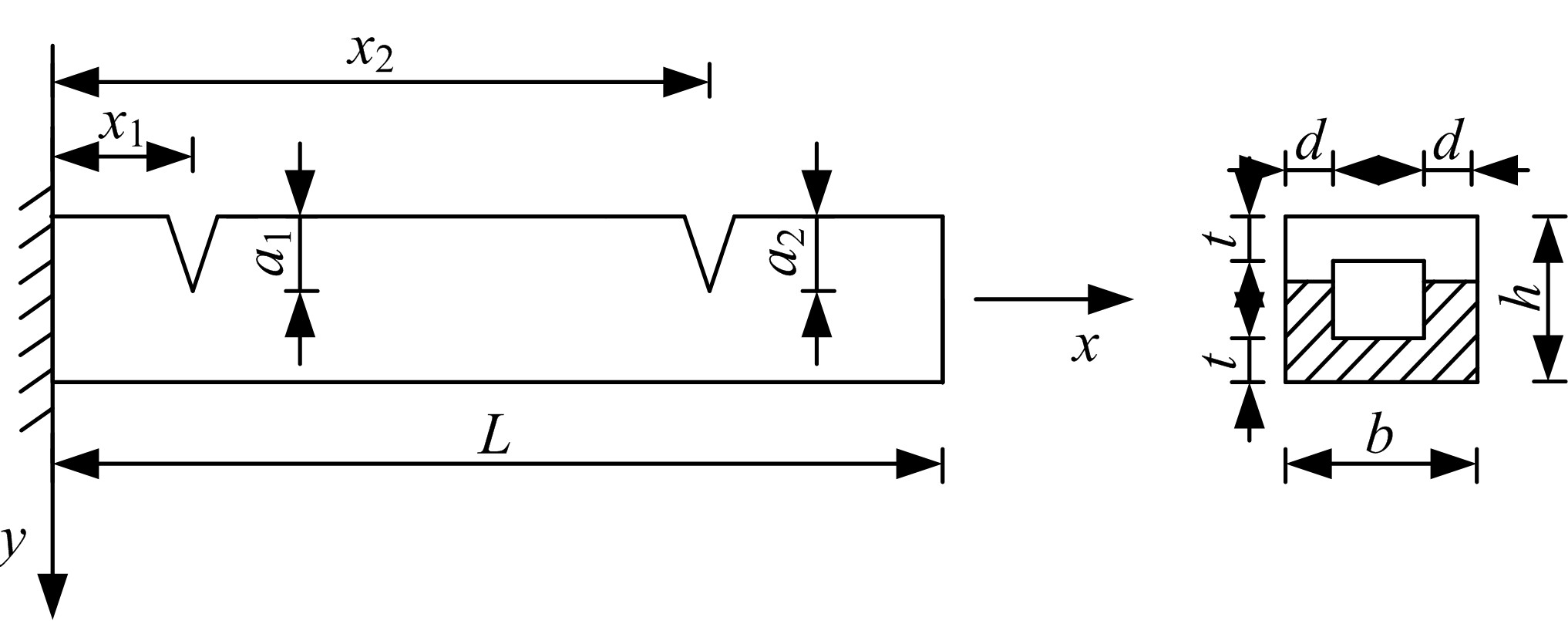
为了准确分析裂缝箱形截面梁的自振特性，基于局部柔度形成的基本原理推导了箱型截面梁在深裂缝和浅裂缝情况下的附加柔度矩阵，得到了裂缝梁单元的刚度矩阵，进而形成了基于有限元方法的裂缝箱梁桥自振特性分析方法。对裂缝悬臂钢梁进行动力特性实验，将实验结果与自振频率计算结果进行对比分析以验证本文方法的准确性与可靠性。对连续钢筋混凝土箱梁进行数值分析，剖析了裂缝位置、深度和数量对箱梁桥的自振频率的影响以及裂缝对振型的影响。

关键词: 桥梁工程, 箱梁桥, 裂缝, 自振特性

Abstract:

The free vibration characteristics of cracked box girder bridges were analyzed in this paper. Firstly， the additional flexibility matrices of box girder in the cases of deep crack and shallow crack were derived based on the basic principle of local flexibility formation， and the stiffness matrix of cracked beam element was obtained， and then the free vibration characteristic analysis method of cracked box girder bridge based on finite element method was formed. Next， the dynamic characteristics of the cracked cantilever steel beam were tested， and the experimental results were compared with the natural frequency calculation results to verify the accuracy and reliability of the proposed method. Finally， the numerical analysis of continuous reinforced concrete box girder was carried out， and the influence of crack location， depth and number on the natural frequency of box girder bridge and the influence of crack on vibration mode were analyzed.

Key words: bridge engineering, box section beam bridge, crack, free vibration characteristics

中图分类号: 

  • U446

图1

裂缝梁单元"

图2

裂缝箱型横截面"

图3

悬臂钢梁几何尺寸"

图4

箱型截面梁测试现场"

图5

悬臂钢梁前2阶自振频率改变率"

图6

桥梁立面图（单位：cm）"

图7

桥梁横截面（单位：cm）"

图8

悬臂钢梁前2阶自振频率改变率"

图9

连续箱梁桥前两阶自振频率改变率"

图10

连续箱梁桥前两阶振型"

1 程永春,谭国金,刘寒冰,等. 基于特征解统计特性的桥梁损伤识别[J]. 吉林大学学报: 工学版, 2008, 37(4): 812-816.
Cheng Yong-chun,Tan Guo-jin,Liu Han-bing, et al. Damage identification of bridge structure based on statistical properties of eigen-solution[J]. Journal of Jilin University (Engineering and Technology Edition), 2008, 37(4): 812-816.
2 程永春,谭国金,刘寒冰, 等. 车辆作用下的公路简支梁桥测试频率[J]. 吉林大学学报: 工学版, 2009, 39(6): 1492-1496.
Cheng Yong-chun,Tan Guo-jin,Liu Han-bing, et al. Test frequencies freely supported beam of highway bridge under effect of vehicles[J]. Journal of Jilin University (Engineering and Technology Edition), 2009, 39(6): 1492-1496.
3 Torabi K, Afshari H, Aboutalebi, F H. A DQEM for transverse vibration analysis of multiple cracked non-uniform Timoshenko beams with general boundary conditions[J]. Computers and Mathematics with Applications, 2014, 67(3): 527-541.
4 Zheng T, Ji T. An approximate method for determining the static deflection and natural frequency of a cracked beam[J]. Journal of Sound and Vibration, 2012, 331(11): 2654-2670.
5 Tan G J, Shan J H, Wu C L, et al. Direct and inverse problems on free vibration of cracked multiple I-section beam with different boundary conditions[J]. Advances in Mechanical Engineering, 2011, 9(11): 1-17.
6 Tan G J, Liu Y, Gong Y F, et al. Free vibration of the cracked non-uniform beam with cross section varying as polynomial functions[J]. KSCE Journal of Civil Engineering, 2018, 22(11): 4530-4546.
7 Ostachowicz W M, Krawczuk M. Analysis of the effect of cracks on the natural frequencies of a cantilever beam[J]. Journal of Sound and Vibration, 1991, 150(2): 191-201.
8 Shifrin E I, Ruotolo T. Natural frequencies of a beam with an arbitrary number of cracks[J]. Journal of Sound and vibration, 1999, 222(3): 409-423.
9 Abdel W M, Roeck G D, Peeters B. Parameterization of damage in reinforced concrete structures using modal updating[J]. Journal of Sound and Vibration, 1999, 228(4): 717-730.
10 Yin X F, Liu Y, Kong B. Vibration behaviors of a damaged bridge under moving vehicular loads[J]. Structural Engineering and Mechanics, 2016, 58(2): 199-216.
11 Law S S, Zhu X Q. Dynamic behavior of damaged concrete bridge structures under moving vehicular loads[J]. Engineering Structures, 2004, 26( 9): 1279-1293.
12 Lin H P. Direct and inverse methods on free vibration analysis of simply supported beams with a crack[J]. Engineering Structures, 2004, 26(4): 427-436.
13 Attar M. A transfer matrix method for free vibration analysis and crack identification of stepped beams with multiple edge cracks and different boundary conditions[J]. International Journal of Mechanical Sciences, 2012, 57(1): 19-33.
14 Tan G J, Shan J H, Wu C L andet al. Free vibration analysis of cracked Timoshenko beams carrying spring-mass systems[J]. Structural Engineering and Mechanics, 2017, 63(4): 551-565.
15 Zheng D Y, Kessissoglou N J. Free vibration analysis of a cracked beam by finite element method[J]. Journal of Sound and Vibration, 2004, 273(3): 457-475.
16 Qian G L, Gu S N, Jiang J S. The dynamic behavior and crack detection of a beam with a crack[J]. Journal of Sound and Vibration, 1990, 138(2): 233-243.
17 Nguyen K V. Mode shapes analysis of a cracked beam and its application for crack detection[J]. Journal of Sound and Vibration, 2014, 333(3): 848-872.
18 Dimarogonas A D, Papadopoulos C A. Vibration of cracked shafts in bending[J]. Journal of Sound and Vibration, 1983, 91(4): 583-593.
19 Tada H, Paris P C, Irwin G R. The Stress Analysis of Cracks Handbook[M]. New York: ASME Press, 2000.
20 Kisa M, Brandon J. The effects of closure of cracks on the dynamics of a cracked cantilever beam[J]. Journal of Sound and Vibration, 2000, 238(1): 1-18.
21 Cheng W L. Determination of the mode I stress intensity factors for an edge-cracked beam with fixed ends[J]. Engineering Fracture Mechanics, 1999,63(2): 193-208.
22 Zienkiewicz O C, Taylor R L. The Finite Element Method[M]. 4th edNew York: McGraw-Hill, 1988.
[1] 陈华,陈耀嘉,谢斌,王鹏凯,邓朗妮. CFRP筋粘结式锚固体系界面失效演化机制及粘结强度计算[J]. 吉林大学学报(工学版), 2020, 50(5): 1698-1708.
[2] 宫亚峰,宋加祥,毕海鹏,谭国金,胡国海,林思远. 装配式箱涵结构缩尺模型静载试验及有限元分析[J]. 吉林大学学报(工学版), 2020, 50(5): 1728-1738.
[3] 高昊,王君杰,刘慧杰,王剑明. 连续梁桥地震行为可控设计准则及实用装置[J]. 吉林大学学报(工学版), 2020, 50(5): 1718-1727.
[4] 蒲黔辉,刘静文,赵刚云,严猛,李晓斌. 高性能树脂混凝土加固混凝土偏压柱承载力理论分析[J]. 吉林大学学报(工学版), 2020, 50(2): 606-612.
[5] 张云龙,郭阳阳,王静,梁东. 钢-混凝土组合梁的固有频率及其振型[J]. 吉林大学学报(工学版), 2020, 50(2): 581-588.
[6] 王伯昕,杨海涛,王清,高欣,陈小旭. 基于补充改进集合经验模态分析法⁃多尺度排列熵分析桥梁振动信号优化滤波方法[J]. 吉林大学学报(工学版), 2020, 50(1): 216-226.
[7] 张淼,钱永久,张方,朱守芹. 基于增大截面法的混凝土加固石拱桥空间受力性能试验分析[J]. 吉林大学学报(工学版), 2020, 50(1): 210-215.
[8] 贾毅,赵人达,王永宝,李福海. 多跨长联连续梁桥粘滞阻尼器参数敏感性分析[J]. 吉林大学学报(工学版), 2019, 49(6): 1871-1883.
[9] 钟春玲,梁东,张云龙,王静. 体外预应力加固简支梁自振频率计算[J]. 吉林大学学报(工学版), 2019, 49(6): 1884-1890.
[10] 白伦华,沈锐利,张兴标,王路. 自锚式悬索桥的面内稳定性[J]. 吉林大学学报(工学版), 2019, 49(5): 1500-1508.
[11] 赵金钢,张明,占玉林,谢明志. 基于塑性应变能密度的钢筋混凝土墩柱损伤准则[J]. 吉林大学学报(工学版), 2019, 49(4): 1124-1133.
[12] 万世成,黄侨,关健,郭赵元. 预应力碳纤维板加固钢⁃混凝土组合连续梁负弯矩区试验[J]. 吉林大学学报(工学版), 2019, 49(4): 1114-1123.
[13] 李万恒,申林,王少鹏,赵尚传. 基于多阶段分区域动力测试的桥梁结构损伤评估[J]. 吉林大学学报(工学版), 2019, 49(3): 773-780.
[14] 惠迎新,毛明杰,刘海峰,张尚荣. 跨断层桥梁结构地震响应影响[J]. 吉林大学学报(工学版), 2018, 48(6): 1725-1734.
[15] 郑一峰, 赵群, 暴伟, 李壮, 于笑非. 大跨径刚构连续梁桥悬臂施工阶段抗风性能[J]. 吉林大学学报(工学版), 2018, 48(2): 466-472.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
版权所有 © 《吉林大学学报(工学版)》编辑部
地址：长春市人民大街5988号　电话：+86-431-85095297　传真：+86-431-85094074　E-mail: xbgxb@jlu.edu.cn
本系统由北京玛格泰克科技发展有限公司设计开发