基于移动最小二乘法的稳健重构方法

doi:10.13229/j.cnki.jdxbgxb20191050

摘要/Abstract

摘要：

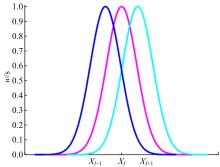
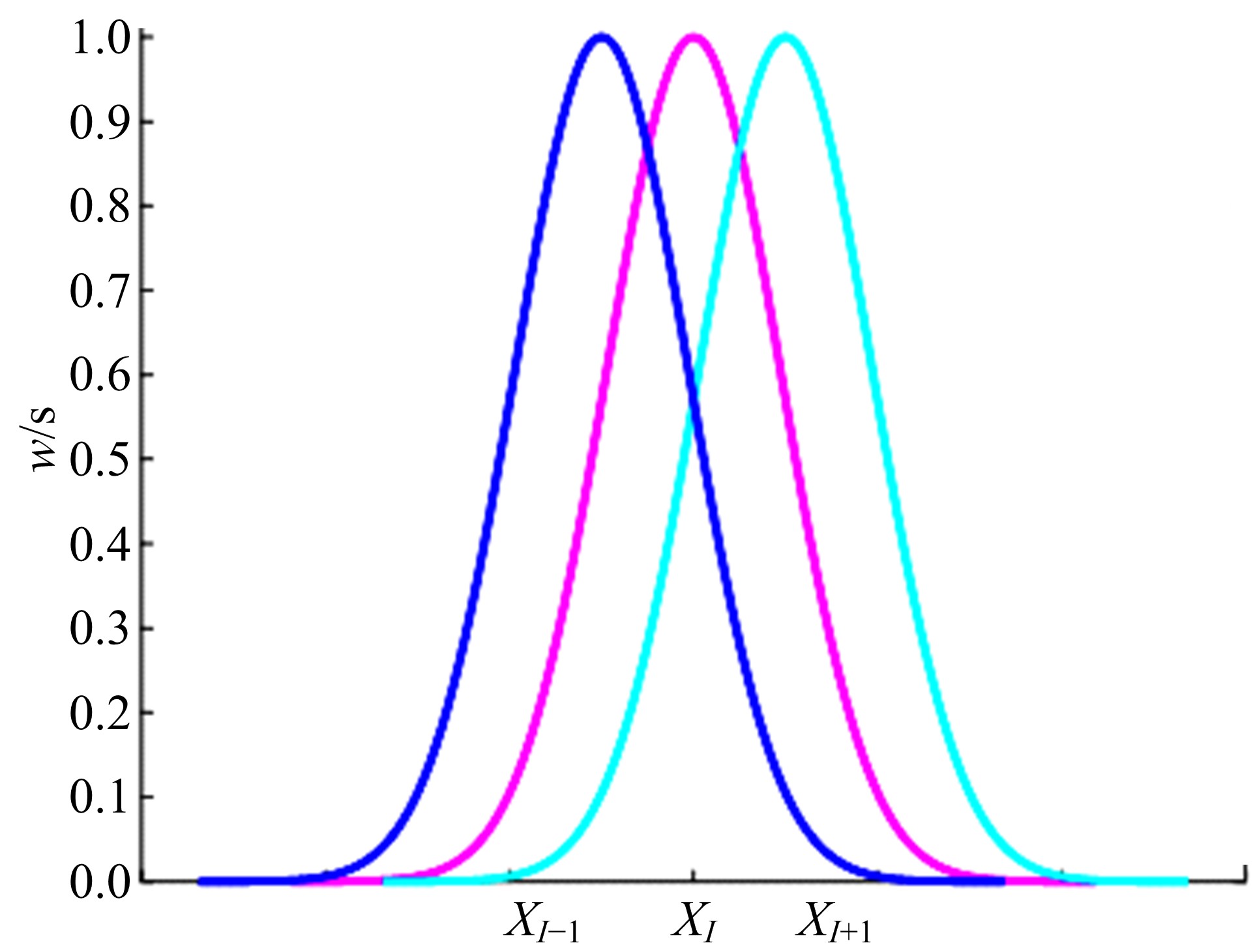
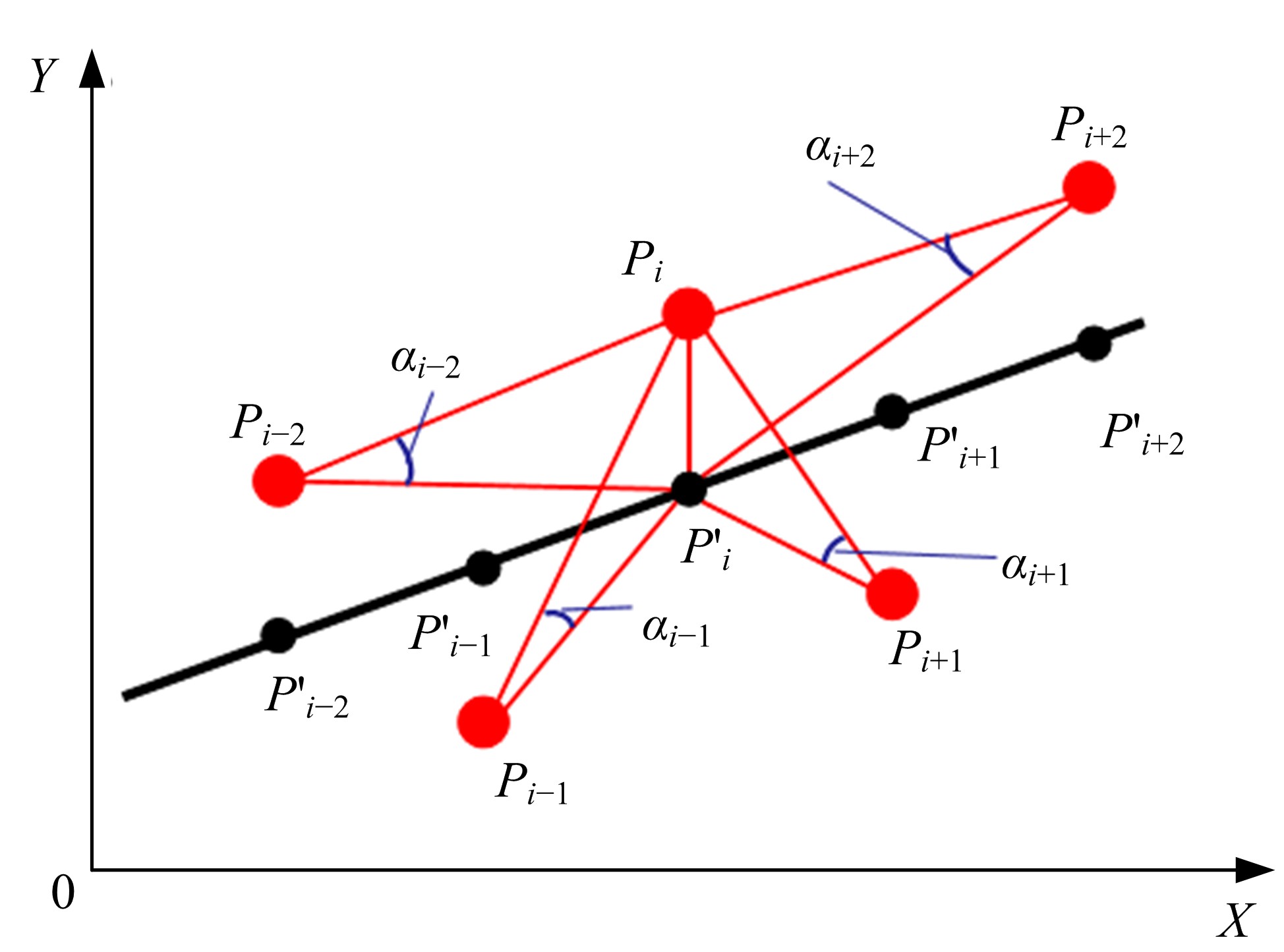
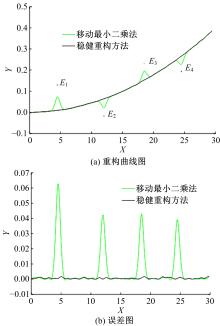
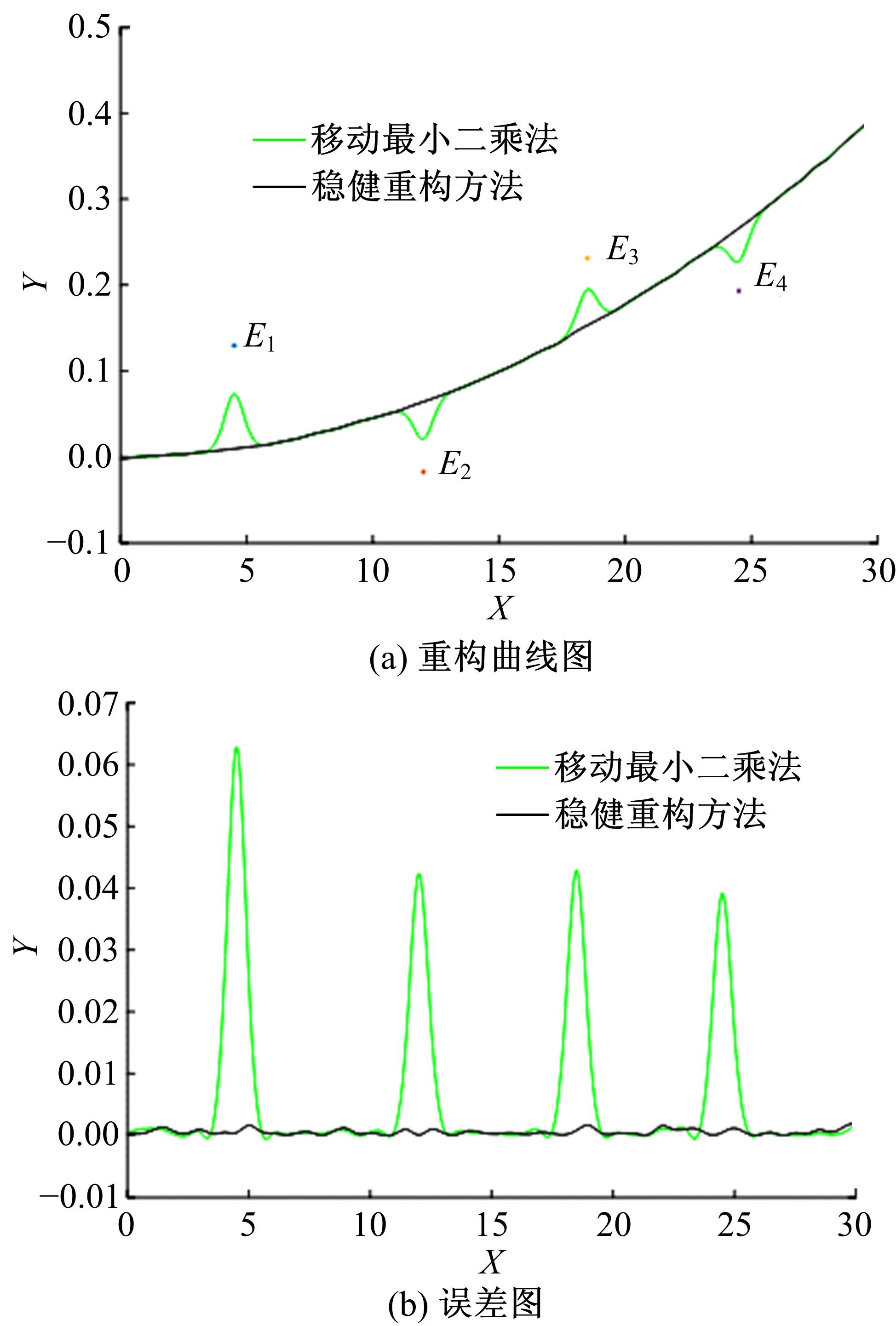
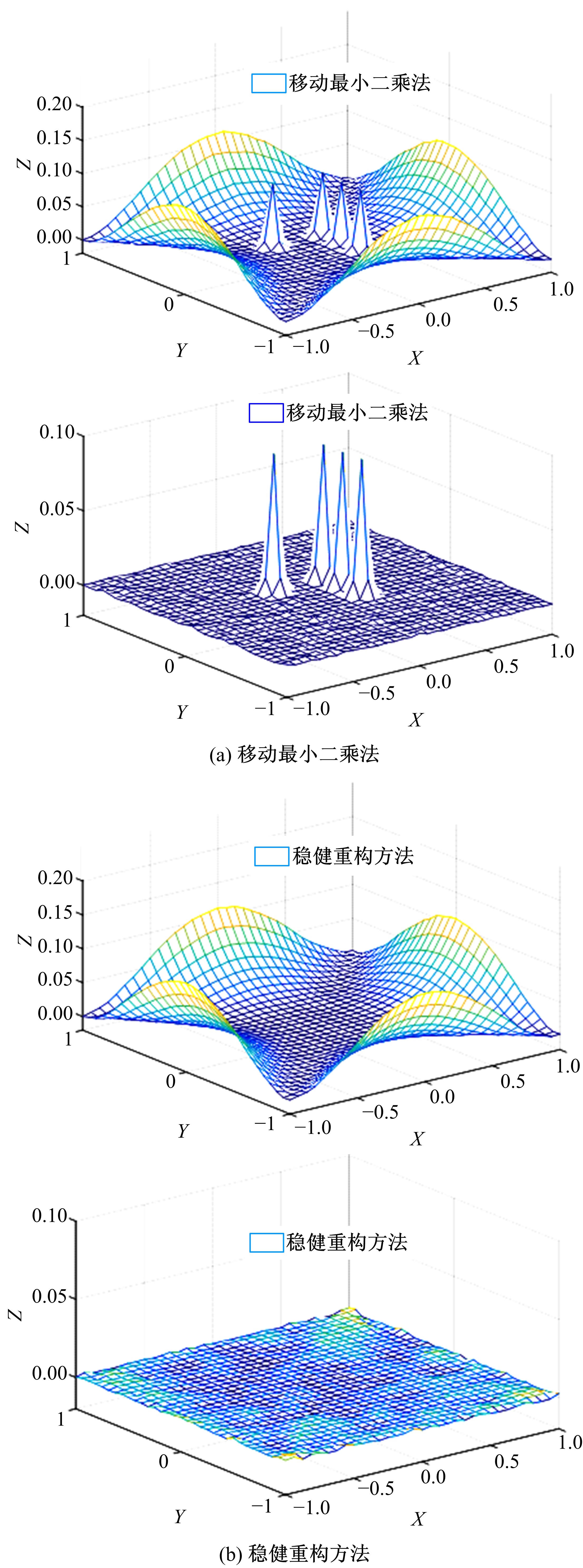
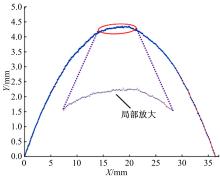
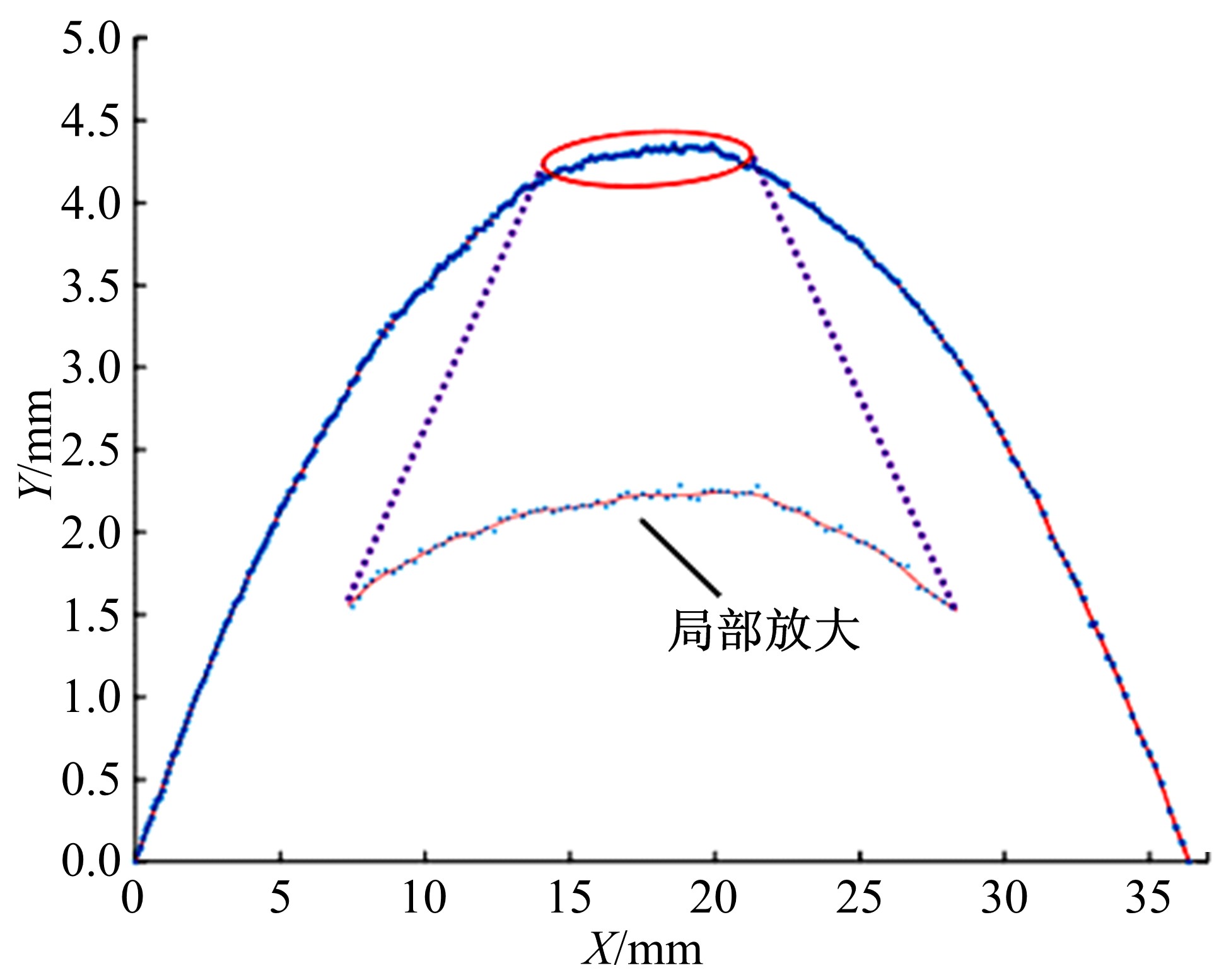
在实际工程问题中，由于人为或环境等外界因素的影响，通过仪器测量获得的数据，不可避免地会存在粗大误差，以某种方式偏离测量数据，导致数据重构的精度不稳定。针对包含粗大误差的测量数据，本文提出一种基于移动最小二乘法的稳健重构方法，该方法对支持域内节点采用最小二乘法进行拟合，将生成的拟合点根据引入的几何特征参数α，量化各节点的异常程度并剔除异常值。对支持域内的剩余节点采用加权最小二乘法确定局部拟合系数，移动支持域完成全域的曲线曲面重构。在每个支持域内仅剔除一个点，就能有效地处理多个粗大误差，且剔除过程无需主观地设定阈值或分配权重。数值模拟与测量实验结果表明：本文方法可有效剔除测量数据中的粗大误差，与传统移动最小二乘法相比，本文数值案例精度能提高60%以上，具有良好的重构稳健性。

关键词: 计算机应用, 移动最小二乘法, 曲线曲面重构, 粗大误差, 稳健性

Abstract:

In practical engineering problems， due to the influence of external factors such as artificial or environmental disturbance， there will inevitably be outliers in the measurement data obtained by instruments. The outliers will deviate from the measurement data in some way， resulting in the instability of the accuracy of data reconstruction. For the measurement data with outliers， a robust reconstruction method based on Moving Least Squares （MLS） is proposed. This method fits the nodes with the least square method in the influence domain. The abnormal degree of generated fitting point is quantified according to the geometric characteristic parameter α， and the outliers is eliminated. The local fitting coefficients are determined with the weight least square by using the remaining nodes in the influence domain， and the curve and surface reconstruction is completed by moving the influence domain. By trimming only one point in each influence domain， the multiple outliers of measurement data can be effectively handled， and it is unnecessary to set threshold values subjectively or assign weights， which avoids the negative influence of manual operations. The numerical simulation and experimental results show that the proposed method can effectively eliminate the outliers in the measurement data. Compared with the MLS method， the accuracy of the numerical case can be improved by more than 60%.

Key words: computer application, moving least squares, curve and surface reconstruction, outliers, robust

中图分类号:

TP391.9

顾天奇,胡晨捷,涂毅,林述温. 基于移动最小二乘法的稳健重构方法[J]. 吉林大学学报(工学版), 2021, 51(2): 685-691.

Tian-qi GU,Chen-jie HU,Yi TU,Shu-wen LIN. Robust reconstruction method based on moving least squares algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(2): 685-691.

图/表 9

图1

图2

表1

案例一两种方法的重构结果"

重构方法	$s$	RMS
移动最小二乘法	0.392 431	0.004 299
稳健重构方法	0.058 993	0.000 375

表1

图3

表2

案例二两种方法的重构结果"

重构方法	$s$	RMS
移动最小二乘法	1.815 587	0.023 557
稳健重构方法	0.742 394	0.003 551

表2

图4

图5

表3

图6

参考文献 20

1	张雄, 刘岩, 马上. 无网格法的理论及应用[J]. 力学进展, 2009, 39(1): 1-36.
	Zhang Xiong, Liu Yan, Ma Shang. Theory and application of meshless method[J]. Progress in Mechanics, 2009, 39(1): 1-36.
2	Lancaster P,Salkauskas K. Surfaces generated by moving least squares methods[J]. Mathematics Computation, 1981, 37: 141-158.
3	韩加坤. 无网格法中MLS参数的选取[J]. 数学学习与研究, 2016(23): 145,147.
	Han Jia-kun. Selection of MLS parameters in meshless method[J]. Mathematics Learning and Research, 2016(23): 145,147.
4	王青青, 李小林. 基于比例移动最小二乘近似的误差分析[J]. 应用数学和力学, 2017, 38(11): 1289-1299.
	Wang Qing-qing, Li Xiao-lin. Error analysis based on proportional moving least square approximation[J]. Applied Mathematics and Mechanics, 2017, 38(11): 1289-1299.
5	Carlos Z. Good quality point sets and error estimates for moving least square approximations[J]. Applied Numerical Mathematics, 2003, 47(3): 575-585.
6	袁占斌, 聂玉峰, 欧阳洁. 基于泰勒基函数的移动最小二乘法及误差分析[J]. 数值计算与计算机应用, 2012, 33(1): 25-31.
	Yuan Zhan-bin, Nie Yu-feng, Jie Ou-yang. Moving least square method and error analysis based on taylor basis function[J]. Numerical Computing and Computer Applications, 2012, 33(1): 25-31.
7	顾天奇, 张雷, 冀世军, 等. 封闭离散点的曲线拟合方法[J]. 吉林大学学报: 工学版, 2015, 45(2): 437-441.
	Gu Tian-qi, Zhang Lei, Ji Shi-jun, et al. Curve fitting method for closed discrete points[J]. Journal of Jilin University (Engineering and Technology Edition), 2015, 45(2): 437-441.
8	李世飞, 王平, 沈振康. 利用移动最小二乘法进行深度图像曲面拟合[J]. 吉林大学学报: 工学版, 2010, 40(1): 229-233.
	Li Shi-fei, Wang Ping, Shen Zhen-kang. Range image surface fitting via moving least squares methods[J]. Journal of Jilin University (Engineering and Technology Edition), 2010, 40(1): 229-233.
9	Liu D, Cheng Y M. The interpolating element-freeGalekin (IEFG) method for three-dimensional pote-ntial problems[J]. Engineering Analysis with Boun-Dary Elements, 2019, 108: 115-123.
10	Wang Q, Zhou W, Feng Y T, et al. An adaptive orthogonal improved interpolating moving least-square method and a new boundary element-free method[J]. Applied Mathematics and Computation, 2019, 353: 347-370.
11	崔鑫, 闫秀天, 李世鹏. 保持特征的散乱点云数据去噪[J]. 光学精密工程, 2017, 25(12): 3169-3178.
	Cui Xin, Yan Xiu-tian, Li Shi-peng. Denoising of scattered point cloud data with preserved features[J]. Optical Precision Engineering, 2017, 25(12): 3169-3178.
12	Liu D L, Shi Y, Tian Y J, et al. Ramp loss least squares support vector machine[J]. Journal of Computation Science, 2016, 14: 61-68.
13	Suykens J A K, Brabanter J D, Lukas L, et al. Weighted least squares support vector m-achines: robustness and sparse approximation[J]. Neurocomputing, 2002, 48(1-4): 85-105.
14	Lin Y L, Hsieh J G, Jeng J H, et al. On least trimmed squares neural networks[J]. Neurocomputing, 2015, 161: 107-112.
15	Yang B, Shao Q M, Pan L, et al. A study on regularized weighted least square support vector classifier[J]. Pattern Recognition Letters, 2018, 108: 48-55.
16	Chen C F, Yan C Q, Li Y Y. A robust weighted least squares support vector regression based on least trimmed squares[J]. Neurocomputing, 2015, 168: 941-946.
17	Wen W, Hao Z F, Yang X W. Robust least squares support vector machine based on recursive outlier elimination[J]. Soft Computing, 2010, 14(11): 1241-1251.
18	Grand R J, Habibullah A C, Adam W, et al. Modified moving least squares with polynomial bases for scattered data approximation[J]. Applied Mathematics and Computation, 2015, 266: 893-902.
19	李睿, 林海荣, 吴小燕. 基于稳健移动最小二乘法的点云数据拟合[J]. 测绘与空间地理信息, 2017, 40(5): 122-124.
	Li Rui, Lin Hai-rong, Wu Xiao-yan. Point cloud data fitting based on robust moving least square method[J]. Mapping and Spatial Geographic Information, 2017, 40(5): 122-124.
20	范晓明, 罗词金, 徐学科, 等. 光学非球面三坐标测量中的像散补偿[J]. 光学精密工程, 2016, 24(12): 3012-3019.
	Fan Xiao-ming, Luo Ci-jin, Xu Xue-ke, et al. Astigmatic compensation in optical aspheric three-coordinate measurement[J]. Optical Precision Engineering, 2016, 24(12): 3012-3019.

相关文章 15

[1]	魏晓辉,周长宝,沈笑先,刘圆圆,童群超. 机器学习加速CALYPSO结构预测的可行性[J]. 吉林大学学报(工学版), 2021, 51(2): 667-676.
[2]	宋元,周丹媛,石文昌. 增强OpenStack Swift云存储系统安全功能的方法[J]. 吉林大学学报(工学版), 2021, 51(1): 314-322.
[3]	方明,陈文强. 结合残差网络及目标掩膜的人脸微表情识别[J]. 吉林大学学报(工学版), 2021, 51(1): 303-313.
[4]	王小玉,胡鑫豪,韩昌林. 基于生成对抗网络的人脸铅笔画算法[J]. 吉林大学学报(工学版), 2021, 51(1): 285-292.
[5]	车翔玖,董有政. 基于多尺度信息融合的图像识别改进算法[J]. 吉林大学学报(工学版), 2020, 50(5): 1747-1754.
[6]	李阳,李硕,井丽巍. 基于贝叶斯模型与机器学习算法的金融风险网络评估模型[J]. 吉林大学学报(工学版), 2020, 50(5): 1862-1869.
[7]	周炳海,何朝旭. 基于线边集成超市的混流装配线动态物料配送调度[J]. 吉林大学学报(工学版), 2020, 50(5): 1809-1817.
[8]	蒋磊,管仁初. 基于多目标进化算法的人才质量模糊综合评价系统设计[J]. 吉林大学学报(工学版), 2020, 50(5): 1856-1861.
[9]	赵宏伟,刘晓涵,张媛,范丽丽,龙曼丽,臧雪柏. 基于关键点注意力和通道注意力的服装分类算法[J]. 吉林大学学报(工学版), 2020, 50(5): 1765-1770.
[10]	管乃彦,郭娟利. 基于姿态估计算法的组件感知自适应模型[J]. 吉林大学学报(工学版), 2020, 50(5): 1850-1855.
[11]	刘洲洲,尹文晓,张倩昀,彭寒. 基于离散优化算法和机器学习的传感云入侵检测[J]. 吉林大学学报(工学版), 2020, 50(2): 692-702.
[12]	王晓辉,吴禄慎,陈华伟. 基于法向量距离分类的散乱点云数据去噪[J]. 吉林大学学报(工学版), 2020, 50(1): 278-288.
[13]	张笑东,夏筱筠,吕海峰,公绪超,廉梦佳. 大数据网络并行计算环境中生理数据流动态负载均衡[J]. 吉林大学学报(工学版), 2020, 50(1): 247-254.
[14]	陈蔓,钟勇,李振东. 隐低秩结合低秩表示的多聚焦图像融合[J]. 吉林大学学报(工学版), 2020, 50(1): 297-305.
[15]	金顺福,郄修尘,武海星,霍占强. 基于新型休眠模式的云虚拟机分簇调度策略及性能优化[J]. 吉林大学学报(工学版), 2020, 50(1): 237-246.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed