大跨度斜拉桥拉索的抖振响应计算方法

doi:10.13229/j.cnki.jdxbgxb20200534

摘要/Abstract

摘要：

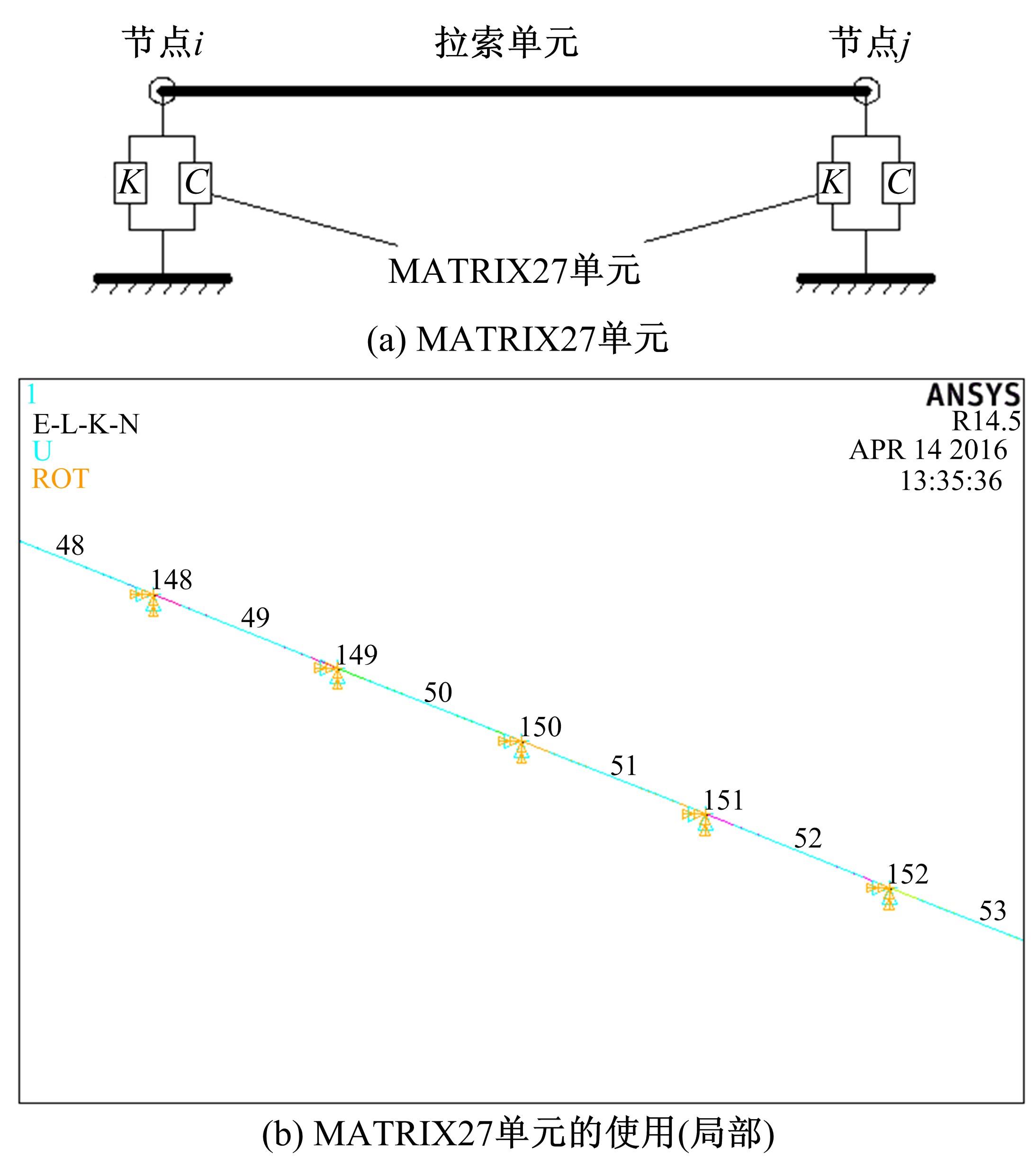
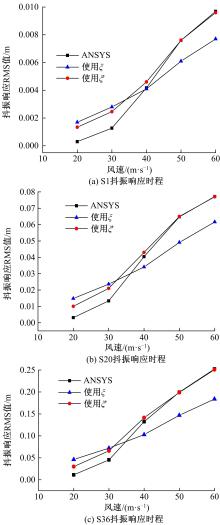
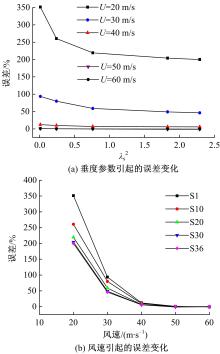
为完善大跨度斜拉桥拉索的抖振响应计算方法，分析了桥梁抖振反应谱法的不足之处，给出了适用于大跨度斜拉桥拉索的气动阻尼计算公式。结合气动阻尼计算公式，对桥梁抖振反应谱法进行改进，进一步提出了适用于大跨度斜拉桥拉索的顺风向抖振响应均方根值的近似计算公式，并对公式的适用性和影响因素进行了分析。研究结果表明：当风速大于40 m/s且拉索无量纲垂度参数在0.76~2.29之间时，该公式具有良好的准确性。运用该公式能方便有效地计算斜拉索的顺风向抖振响应均方根值，可为相关研究及工程分析提供有效方法。

关键词: 桥梁工程, 大跨度斜拉桥, 气动阻尼, 斜拉索, 抖振响应

Abstract:

In order to improve the buffeting response calculation method for cables of long-span cable-stayed bridge， the shortcomings of bridge buffeting response spectrum method are analyzed. Based on bridge buffeting response spectrum method， the aerodynamic damping calculating formula suits for cables in long-span cable-stayed bridge is given， and the approximate formula for the cable buffeting response root mean square along-wind in long-span cable-stayed bridge is proposed. The applicability of the approximate formula is analyzed. The results show that the approximate formula has a good accuracy when the wind speed is higher than 40m/s， meanwhile the sag parameter is between 0.76 and 2.29. The root mean square of cable buffeting response along-wind can be calculated conveniently by this formula， which can provide buffeting response study and engineering analysis with an effective method.

Key words: bridge engineering, long-span cable-stayed bridge, aerodynamic damping, stay cable, buffeting response

中图分类号:

U441

郭殊伦,钟铁毅,闫志刚. 大跨度斜拉桥拉索的抖振响应计算方法[J]. 吉林大学学报(工学版), 2021, 51(5): 1756-1762.

Shu-lun GUO,Tie-yi ZHONG,Zhi-gang YAN. Calculation method of buffeting response for stay cables of long⁃span cable⁃stayed bridge[J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(5): 1756-1762.

图/表 6

图1

图2

表1

拉索参数表"

索号	索长/m	单位长度质量/kg	直径/m	$λ s 2$
S1	136.522	131.5	0.185 52	0.01
S10	231.316	96.9	0.185 52	0.24
S20	359.128	131.5	0.176 34	0.76
S30	493.621	145.0	0.152 12	1.83
S36	576.193	145.0	0.176 34	2.29

表1

图3

图4

图5

参考文献 27

1	Sears W R. Some aspects of non-stationary airfoil theory and its practical application[J]. Journal of Aeronautical Science, 1941, 8(3): 104-108.
2	Liepmann H W. On the application of statistical concepts to the buffeting problem[J]. Journal of Aeronautical Science, 1952, 19(12): 793-800.
3	Davenport A G. The application of statistical concepts to the wind loading of structures[J]. Proceedings of ICE, 1961, 19(8): 449-472.
4	Scanlan R H. The action of flexible bridges under wind, II: buffeting theory[J]. Sound and Vibration, 1978, 60(2): 201-211.
5	张志田, 陈添乐, 吴长青. 基于Küssner函数的不同气动导纳模型对大跨桥梁抖振响应的影响[J]. 振动与冲击, 2019, 38(20): 131-139, 163.
	Zhang Zhi-tian, Chen Tian-le, Wu Chang-qing. Effects of Küssner-function-based aerodynamic admittance models on the buffeting responses of a long-span bridge[J]. Journal of Vibration and Shock, 2019, 38(20): 131-139, 163.
6	Yang Y, Li M S, Su Y, et al. Aerodynamic admittance of a 5:1 rectangular cylinder in turbulent flow[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 189: 125-134.
7	Yang Y, Li M S, Liao H L. Three-dimensional effects on the transfer function of a rectangular-section body in turbulent flow[J]. Journal of Fluid Mechanics, 2019, 872: 348-366.
8	Li M, Li M S, Su Y. Experimental determination of the two-dimensional aerodynamic admittance of typical bridge decks[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 193: 103975.
9	Ma C M, Wang J X, Li Q S, et al. 3D aerodynamic admittances of streamlined box bridge decks[J]. Engineering Structures, 2019, 179: 321-331.
10	Ma C M, Duan Q S, Li Q S, et al. Aerodynamic characteristics of a long-span cable-stayed bridge under construction[J]. Engineering Structures, 2019, 184: 232-246.
11	Yan L, Zhu L D, He X H, et al. Experimental determination of aerodynamic admittance functions of a bridge deck considering oscillation effect[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 190: 83-97.
12	苏益, 李明水. 大跨度桥梁抖振响应的直接估算方法[J]. 中国公路学报, 2019, 32(10): 84-95.
	Su Yi, Li Ming-shui. Direct estimation of buffeting response of long-span bridges[J]. China Journal of Highway and Transport, 2019, 32(10): 84-95.
13	Li M, Li M S, Zhong Y Z, et al. Buffeting response evaluation of long-span bridges with emphasis on the three-dimensional effects of gusty winds[J]. Journal of Sound and Vibration, 2019, 439: 156-172.
14	陶天友, 王浩. 大跨度桥梁主梁节段模型非平稳抖振时域模拟与分析[J]. 振动工程学报, 2019, 32(5): 830-836.
	Tao Tian-you, Wang Hao. Time-domain simulation and analysis of nonstationary buffeting responses of girder section model of a long-span bridge[J]. Journal of Vibration Engineering, 2019, 32(5): 830-836.
15	苏延文, 黄国庆, 曾永平. 强弱非平稳风速对大跨桥梁抖振响应影响研究[J]. 铁道工程学报, 2019, 36(12): 41-47.
	Su Yan-wen, Huang Guo-qing, Zeng Yong-ping. Research on the effects of buffeting responses of a long-span bridge subjected to weak and strong non-stationary wind events[J]. Journal of Railway Engineering Society, 2019, 36(12): 41-47.
16	项海帆, 陈伟, 顾明. 桥梁抖振反应谱的实用计算方法[J]. 土木工程学报, 1995, 28(3): 3-8.
	Xiang Hai-fan, Chen Wei, Gu Ming. A practical calculation method for bridge buffeting response spectrum[J]. China Civil Engineering Journal, 1995, 28(3): 3-8.
17	陈伟. 大跨度桥梁抖振反应谱研究[D]. 上海: 同济大学木工程学院, 1993.
	Chen Wei. Study on buffeting response spectrum of long-span bridges[D]. Shanghai: School of Civil Engineering, Tongji University, 1993.
18	项海帆. 现代桥梁抗风理论与实践[M]. 北京: 人民交通出版社, 2005.
19	.公路桥梁抗风设计规范[S].
20	Matsumoto M, Chen X, Shiraishi N. Buffeting analysis of long span bridge with aerodynamic coupling[C]∥Proceedings of 13th National Symposium on Wind Engineering, Japan Association for Wind Engineering, Japan, 1994: 227-232.
21	Chen X, Matsumoto M, Kareem A. Aerodynamic coupled effects on flutter and buffeting of bridges[J]. Journal of Engineering Mechanics ASCE, 126(1): 2000, 17-26.
22	胡晓伦. 大跨度斜拉桥颤抖振响应及静风稳定性分析[D]. 上海: 同济大学木工程学院, 2006.
	Hu Xiao-lun. Flutter, buffeting and aerostatic stability analysis for long-span cable-stayed bridges[D]. Shanghai: School of Civil Engineering, Tongji University, 2006.
23	郑一峰, 赵群, 暴伟, 等. 大跨径刚构连续梁桥悬臂施工阶段抗风性能[J].吉林大学学报: 工学版, 2018, 48(2): 466-472.
	Zheng Yi-feng, Zhao Qun, Bao Wei, et al. Wind resistance performance of long-span continuous rigid-frame bridge in cantilever construction stage[J]. Journal of Jilin University(Engineering and Technology Edition), 2018, 48(2): 466-472.
24	兰成. 斜拉索振动及其基于性能的减振设计[D]. 上海: 同济大学木工程学院, 2009.
	Lan Cheng. Vibration of stay cable and vibration damping design based on its performance[D]. Shanghai: School of Civil Engineering, Tongji University, 2009.
25	姜浩, 郭学东, 张艳辉. 基于时域分析的风载激励下桥梁结构动力特性识别[J]. 吉林大学学报: 工学版, 2011, 41(5): 1279-1283.
	Jiang Hao, Guo Xue-dong, Zhang Yan-hei. Dynamic behavior identification of concrete bridge structure under wind load excitation based on time-domain analysis[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41(5): 1279-1283.
26	江西省交通设计院. 九江长江公路大桥大跨度斜拉桥施工及成桥阶段减振抑振综合技术研究结题报告[R]. 南昌:江西省交通设计院, 2013.
27	李龙安, 苗润池, 屈爱平. 超长斜拉索风致振动控制研究[J]. 地震工程与工程振动, 2014, 34(3): 206-211.
	Li Long-an, Miao Run-chi, Qu Ai-ping. Study on wind-induced vibration control of super-long stay cables[J]. Earthquake Engineering and Engineering Dynamics, 2014, 34(3): 206-211.

相关文章 15

[1]	陈巍,万田保,王忠彬,厉萱,沈锐利. 悬索桥主缆除湿的内部送气管道设计与性能[J]. 吉林大学学报(工学版), 2021, 51(5): 1749-1755.
[2]	高凯,刘纲. 全局临界强度分枝-约界法的有效强度改进[J]. 吉林大学学报(工学版), 2021, 51(2): 597-603.
[3]	宫亚峰,宋加祥,谭国金,毕海鹏,刘洋,单承新. 多车桥梁动态称重算法[J]. 吉林大学学报(工学版), 2021, 51(2): 583-596.
[4]	孔庆雯,谭国金,王龙林,王勇,魏志刚,刘寒冰. 基于有限元方法的裂缝箱梁桥自振特性分析[J]. 吉林大学学报(工学版), 2021, 51(1): 225-232.
[5]	单德山,张潇,顾晓宇,李乔. 斜拉索悬链线构形的伸长量解析计算方法[J]. 吉林大学学报(工学版), 2021, 51(1): 217-224.
[6]	陈华,陈耀嘉,谢斌,王鹏凯,邓朗妮. CFRP筋粘结式锚固体系界面失效演化机制及粘结强度计算[J]. 吉林大学学报(工学版), 2020, 50(5): 1698-1708.
[7]	宫亚峰,宋加祥,毕海鹏,谭国金,胡国海,林思远. 装配式箱涵结构缩尺模型静载试验及有限元分析[J]. 吉林大学学报(工学版), 2020, 50(5): 1728-1738.
[8]	高昊,王君杰,刘慧杰,王剑明. 连续梁桥地震行为可控设计准则及实用装置[J]. 吉林大学学报(工学版), 2020, 50(5): 1718-1727.
[9]	蒲黔辉,刘静文,赵刚云,严猛,李晓斌. 高性能树脂混凝土加固混凝土偏压柱承载力理论分析[J]. 吉林大学学报(工学版), 2020, 50(2): 606-612.
[10]	张云龙,郭阳阳,王静,梁东. 钢-混凝土组合梁的固有频率及其振型[J]. 吉林大学学报(工学版), 2020, 50(2): 581-588.
[11]	王伯昕,杨海涛,王清,高欣,陈小旭. 基于补充改进集合经验模态分析法⁃多尺度排列熵分析桥梁振动信号优化滤波方法[J]. 吉林大学学报(工学版), 2020, 50(1): 216-226.
[12]	张淼,钱永久,张方,朱守芹. 基于增大截面法的混凝土加固石拱桥空间受力性能试验分析[J]. 吉林大学学报(工学版), 2020, 50(1): 210-215.
[13]	贾毅,赵人达,王永宝,李福海. 多跨长联连续梁桥粘滞阻尼器参数敏感性分析[J]. 吉林大学学报(工学版), 2019, 49(6): 1871-1883.
[14]	钟春玲,梁东,张云龙,王静. 体外预应力加固简支梁自振频率计算[J]. 吉林大学学报(工学版), 2019, 49(6): 1884-1890.
[15]	白伦华,沈锐利,张兴标,王路. 自锚式悬索桥的面内稳定性[J]. 吉林大学学报(工学版), 2019, 49(5): 1500-1508.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed