冗余机械臂运动学逆解的求解优化方法

doi:10.13229/j.cnki.jdxbgxb.20220099

摘要/Abstract

摘要：

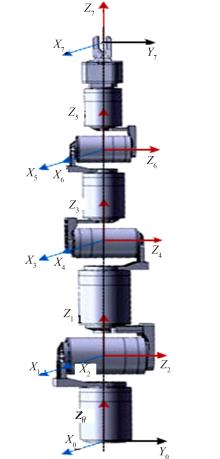
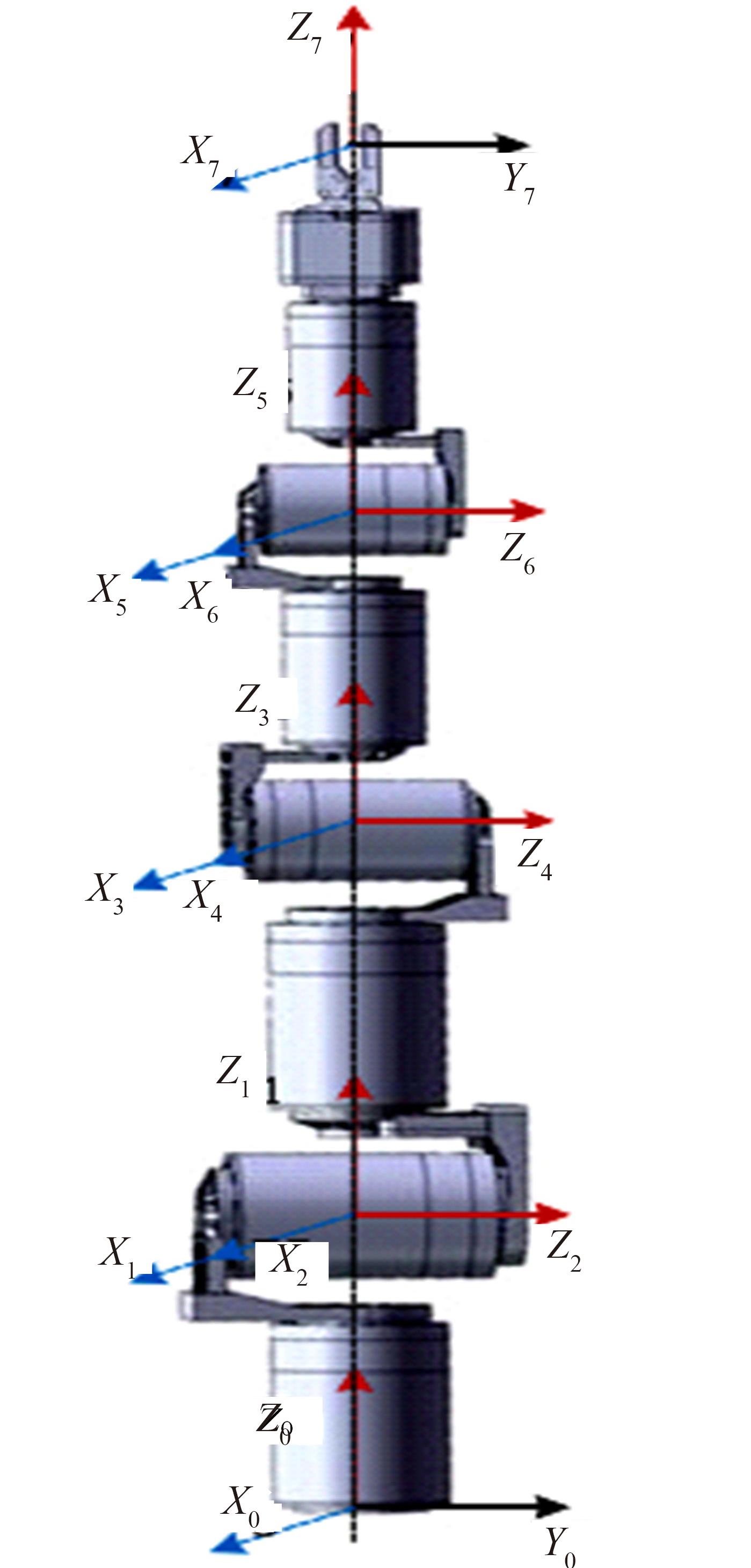
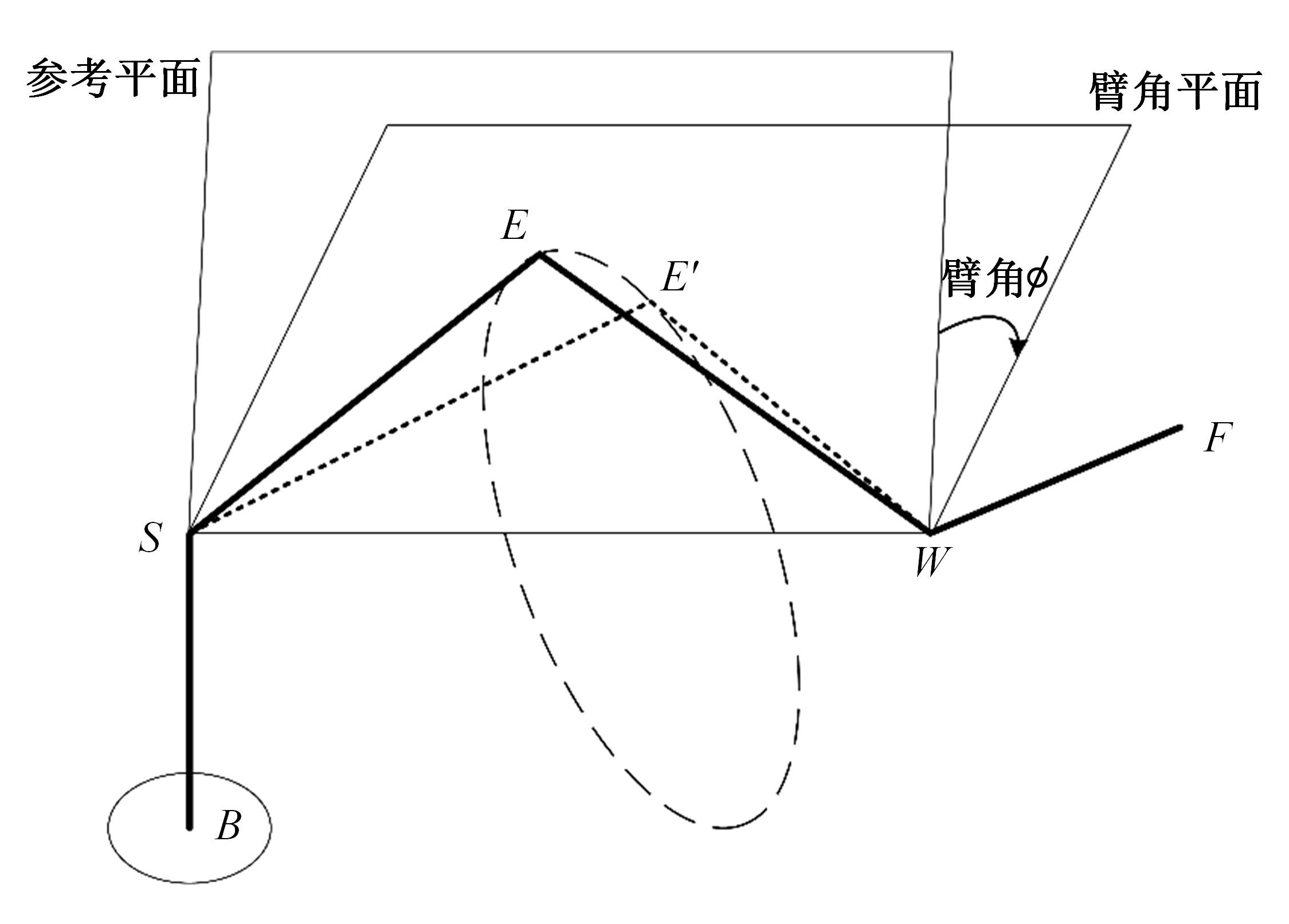
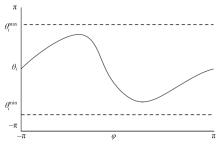
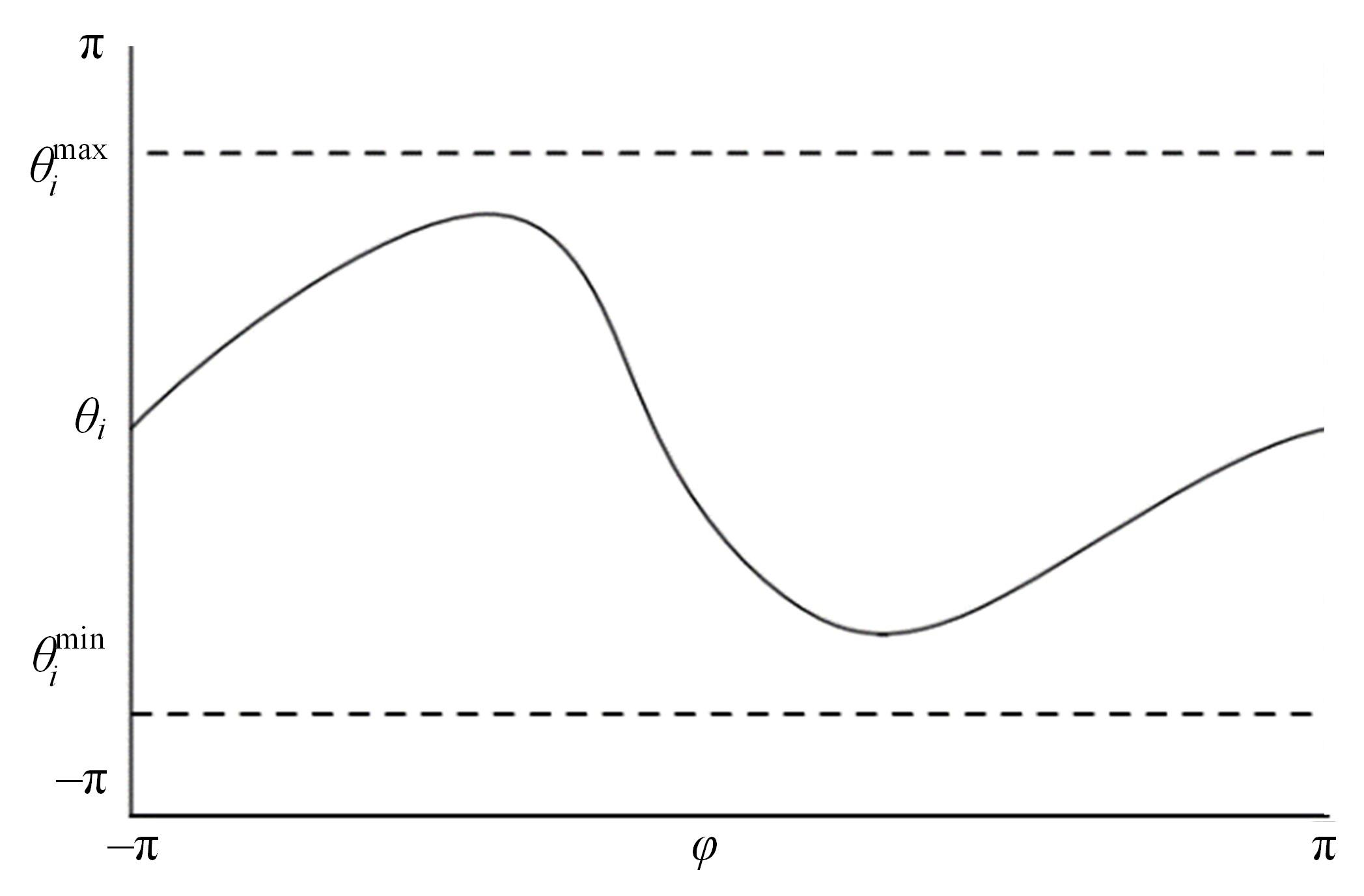
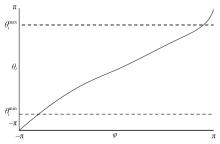
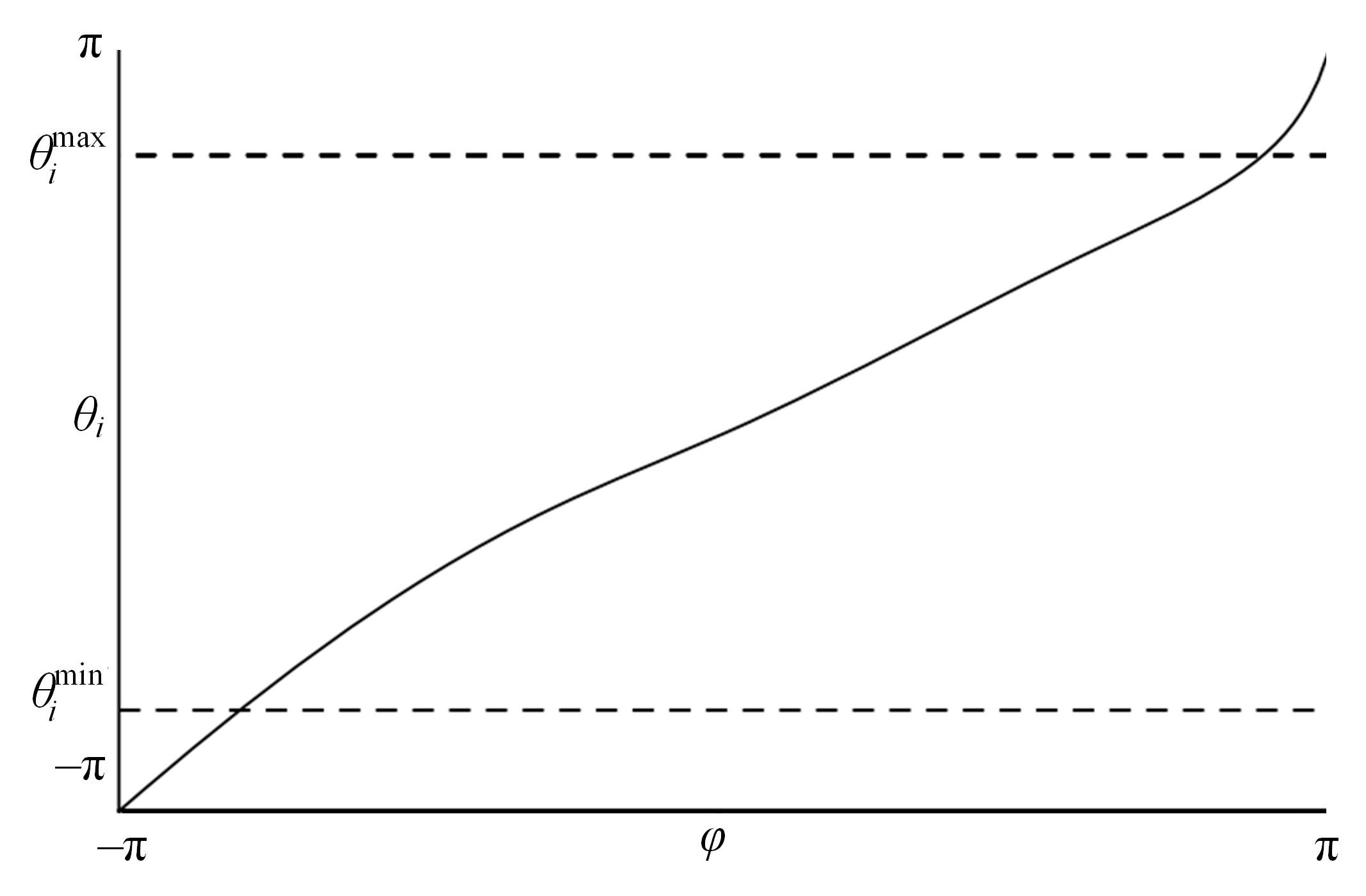
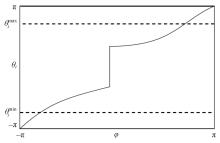
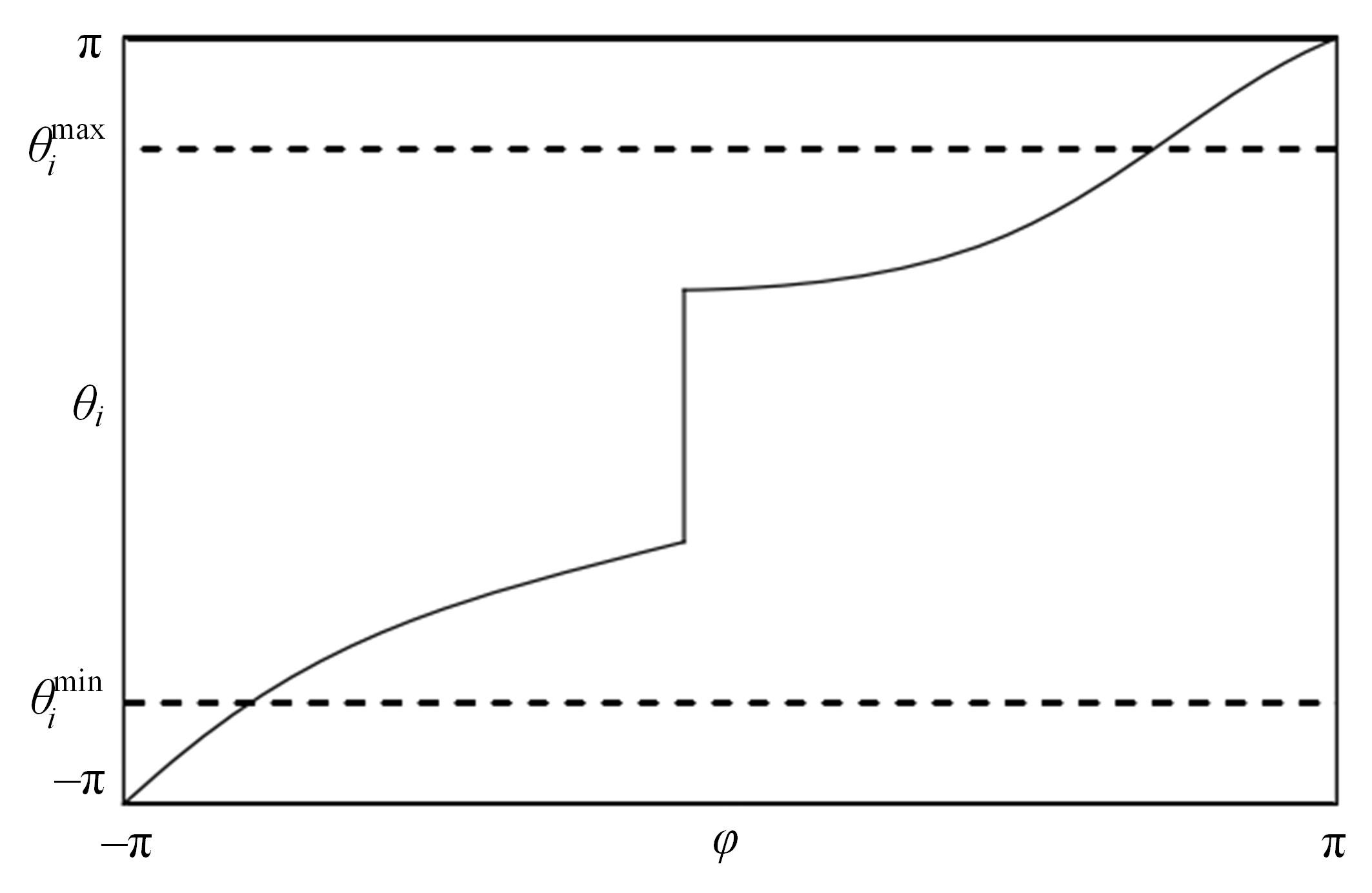
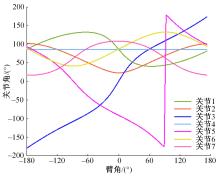
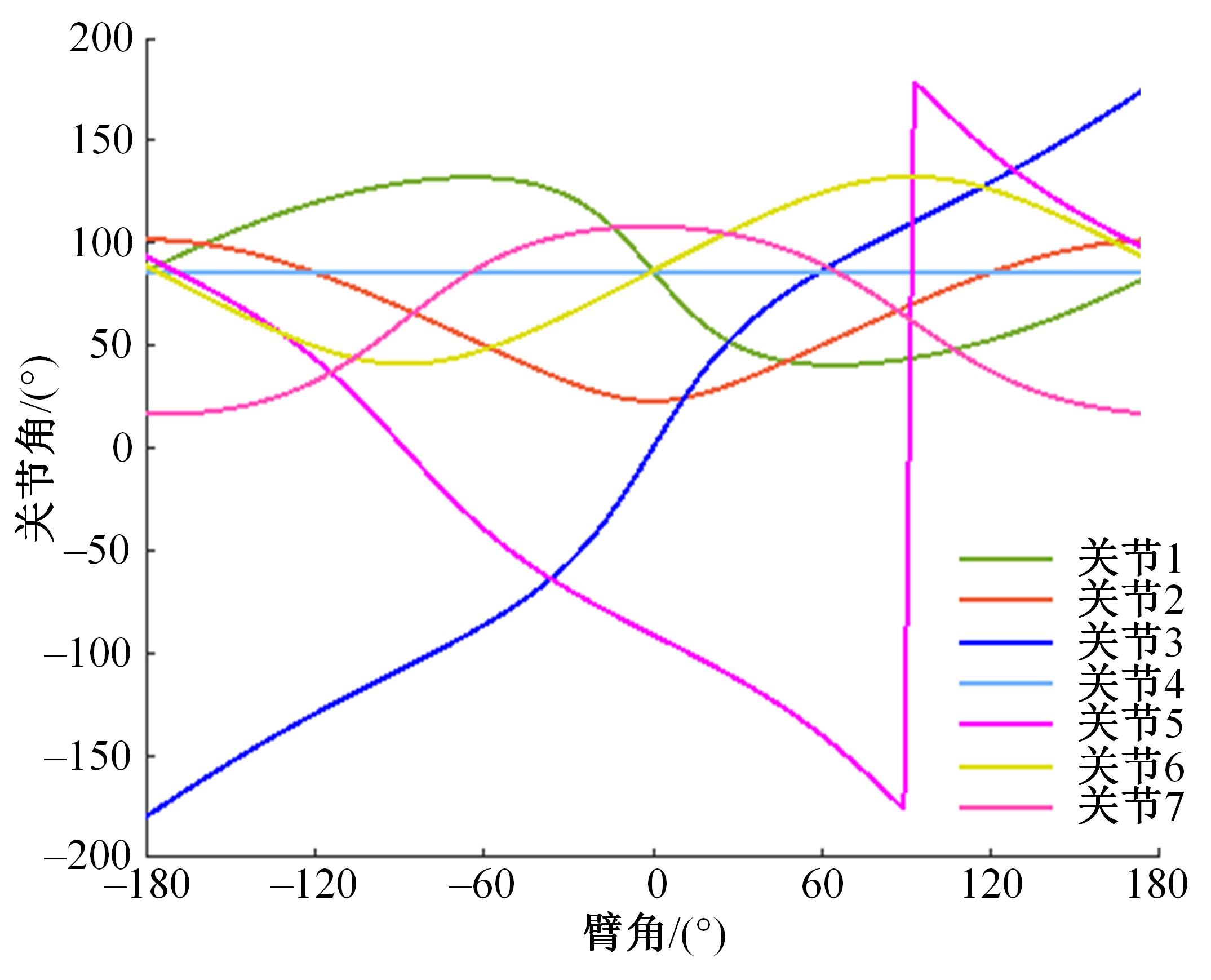
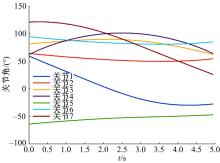
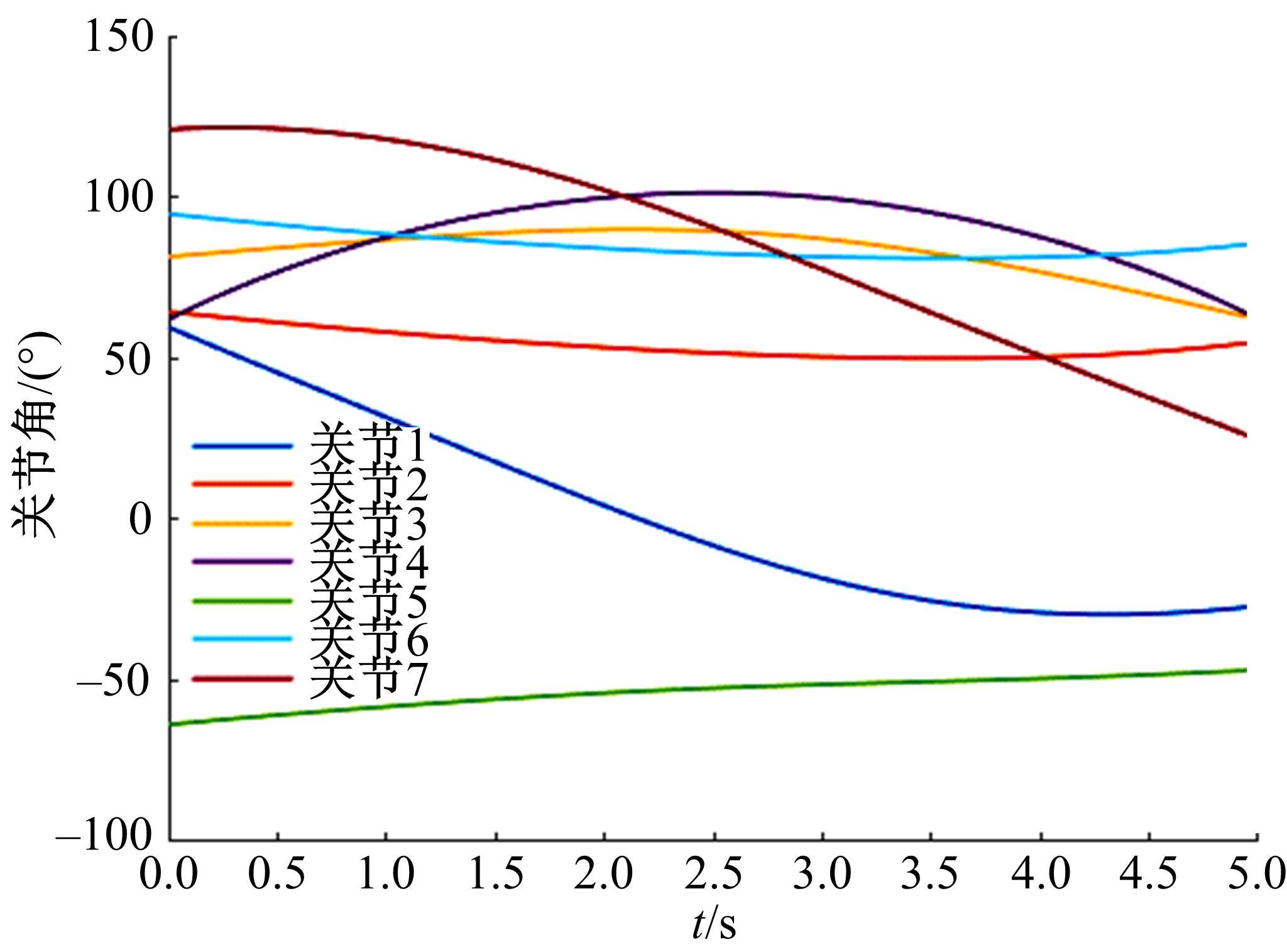
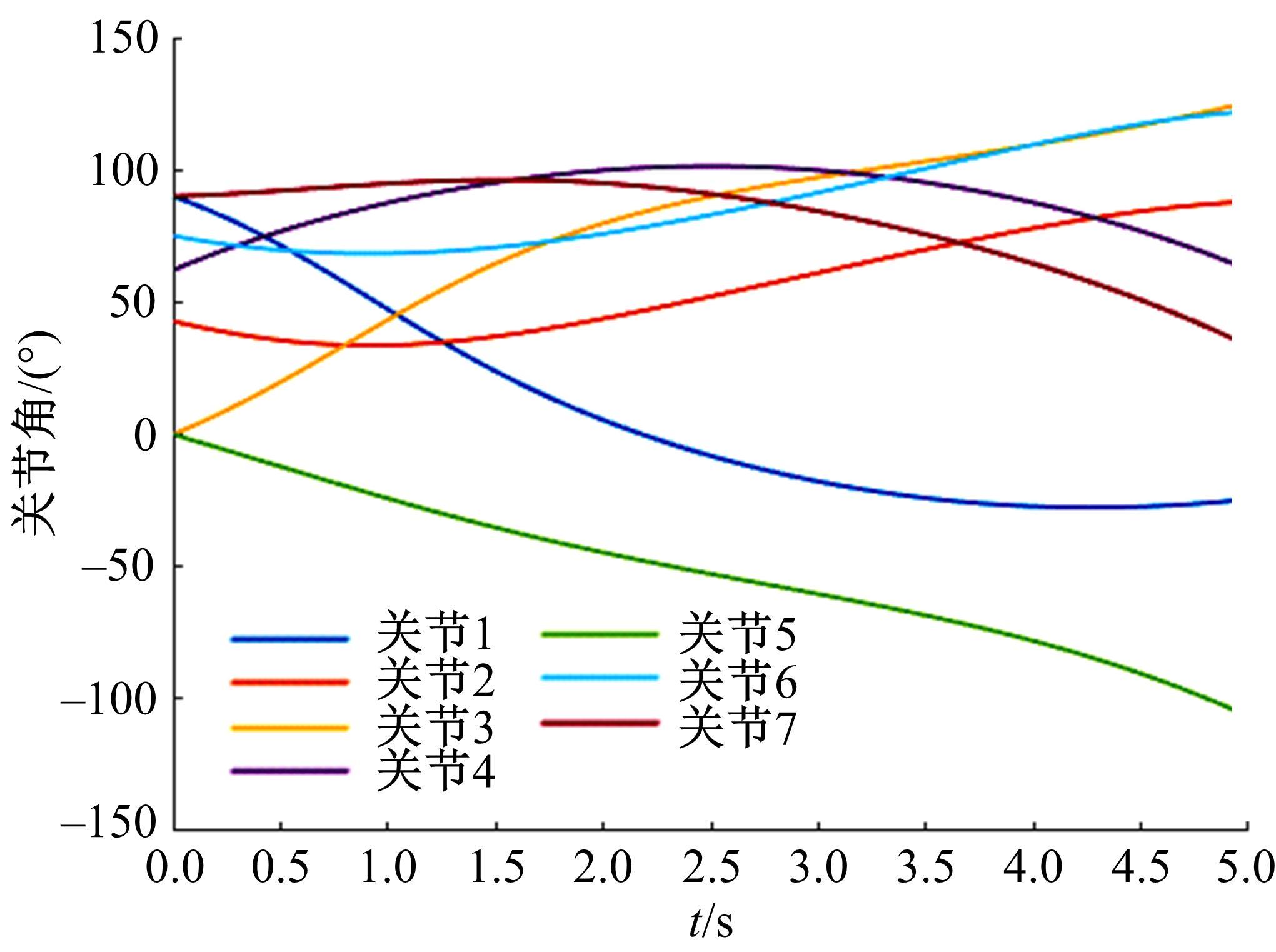
为解决仿人冗余机械臂逆运动学的求解问题，本文提出了一种逆运动学求解优化方法。通过引入臂角参数建立了逆解的解析解公式，根据关节限位进一步分析了不同形式解析解下的臂角可行区间。此外，提出了综合考虑关节避限和能耗最优的目标函数，通过自适应权重参数调节任务优先级，并引入粒子群优化算法得出最优解。实验结果表明，该算法能求出给定臂角的所有解，并且能选出满足关节避限和低能耗的最优解，对于冗余机械臂的轨迹规划有较好的应用意义。

关键词: 冗余机械臂, 逆运动学, 解析解, 关节限位, 能耗最优, 粒子群优化算法

Abstract:

To solve the inverse kinematics of humanoid redundant manipulator， an optimized method was proposed. The analytical solution of the inverse kinematics was established by introducing the arm angle parameters， and the feasible range of the arm angle under different forms of analytical solutions was further analyzed according to the joint limit. In addition， an objective function considering joint limit avoidance and optimal energy consumption was proposed. Tasks， priority was adjusted through adaptive weight parameters， and the particle swarm optimization algorithm was introduced to obtain the optimal solution. Experimental results show that the algorithm can obtain all solutions for a given arm angle and can select the optimal solution that satisfies the joint limit avoidance and low energy consumption. The proposed method has positive application significance for the trajectory movement of the redundant manipulator.

Key words: redundant manipulator, inverse kinematics, analytical solution, joint limit, optimal energy consumption, particle swarm optimization algorithm

中图分类号:

TP242

张铮,朱齐丹,吕晓龙,樊星. 冗余机械臂运动学逆解的求解优化方法[J]. 吉林大学学报(工学版), 2023, 53(12): 3379-3387.

Zheng ZHANG,Qi-dan ZHU,Xiao-long LYU,Xing FAN. Optimized method for solving inverse kinematics of redundant manipulator[J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(12): 3379-3387.

图/表 13

图1

表1

DH参数表"

连杆i	$α i / (°)$	$d i / m$	$θ i / (°)$
1	0	d₁	$θ 1$
2	-90	0	$θ 2$
3	90	d₂	$θ 3$
4	-90	0	$θ 4$
5	90	d₃	$θ 5$
6	-90	0	$θ 6$
7	90	d₄	$θ 7$

表1

图2

图3

图4

图5

图6

表2

图7

图8

图9

图10

表3

参考文献 24

1	徐呈艺, 刘英, 贾民平, 等. 木板抓取冗余机械臂逆运动学求解[J]. 计算机集成制造系统, 2020, 26(12): 3368-3374.
	Xu Cheng-yi, Liu Ying, Jia Min-ping, et al. Inverse kinematics solution of redundant robot arm in picking board[J]. Computer Integrated Manufacturing Systems, 2020, 26(12): 3368-3374.
2	Gong M, Li X, Zhang L. Analytical inverse kinematics and self-motion application for 7-DOF redundant manipulator[J]. IEEE Access, 2019, 7: 18662-18674.
3	段晋军, 甘亚辉, 戴先中, 等. 基于可操作度评价的冗余机器人逆解求解方法[J]. 华中科技大学学报, 2015, (): 45-48, 57.
	Duan Jin-jun, Gan Ya-hui, Dai Xian-zhong, et al. Method of inverse kinematics solution for a redundant manipulator based on manipulability[J]. Journal of Huazhong University of Science and Technology, 2015, (Sup.1): 45-48, 57.
4	卢绍田. 空间冗余机械臂运动优化与轨迹跟踪控制研究[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2019.
	Lu Shao-tian. Research on motion optimization and trajectory tracking control of space redundant manipulator[D]. Harbin: College of Mechanical Engineering, Harbin Institute of Technology, 2019.
5	Zhang X, Fan B, Wang C, et al. An improved weighted gradient projection method for inverse kinematics of redundant surgical manipulators[J]. Sensors, 2021, 21(21): No. 7362.
6	Ito M, Kawatsu K, Shibata M. Kinematic control of redundant manipulators for admitting joint range of motion maximally[J]. IEEJ Journal of Industry Applications, 2017, 6(4): 278-285.
7	Ratajczak J. Design of inverse kinematics algorithms: extended Jacobian approximation of the dynamically consistent Jacobian inverse[J]. Archives of Control Sciences, 2015, 25(1): 35-50.
8	谢宗武, 孙奎, 刘宏. 扩展雅克比方法的冗余度机器人逆运动学应用[J]. 哈尔滨工业大学学报, 2009(5): 34-36.
	Xie Zong-wu, Sun Kui, Liu Hong. Application study on inverse kinematics algorithm of redundant manipulator based on extended Jacobian method[J]. Journal of Harbin Institute of Technology, 2009(5): 34-36.
9	Wan J, Li D, Yao J, et al. A hybrid CHAOS-PSO algorithm for dimensional synthesis of a redundant manipulator based on tracking trajectories without or with singularities[J]. Production Engineering, 2018, 12(5): 579-587.
10	Xiang J, Zhong C, Wei W. General-weighted least-norm control for redundant manipulators[J]. IEEE Transactions on Robotics, 2010, 26(4): 660-669.
11	Chen P, Xiang J, Wei W. A unified weighted least norm method for redundant manipulator control[J]. International Journal of Advanced Robotic Systems, 2016, 13(1): No. 19.
12	房立龙. 仿人双臂协作机器人设计研究[D]. 合肥: 中国科学技术大学工程科学学院, 2015.
	Fang Li-long. Research on the design of human-like dual-arm collaborative robot[D]. Hefei: College of Mechatronic Engineering, University of Science and Technology of China, 2015.
13	Wang X, Zhang D, Zhao C. Inverse kinematics of a 7R 6-DOF robot with nonspherical wrist based on transformation into the 6R robot[J]. Mathematical Problems in Engineering, 2017, 2017: 1-12.
14	Asfour T, Dillmann R. Human-like motion of a humanoid robot arm based on a closed-form solution of the inverse kinematics problem[C]∥Proceedings 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003), Washington, D C, USA, 2003: 1407-1412.
15	Shimizu M, Kakuya H, Yoon W K, et al. Analytical inverse kinematic computation for 7-DOF redundant manipulators with joint limits and its application to redundancy resolution[J]. IEEE Transactions on Robotics, 2008, 24(5): 1131-1142.
16	Yan L, Mu Z, Xu W. Analytical inverse kinematics of a class of redundant manipulator based on dual arm-angle parameterization[C]∥2014 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Washington, D C, USA, 2014: 3744-3749.
17	Faria C, Ferreira F, Erlhagen W, et al. Position-based kinematics for 7-DoF serial manipulators with global configuration control, joint limit and singularity avoidance[J]. Mechanism and Machine Theory, 2018, 121(9): 317-334.
18	霍希建, 刘伊威, 姜力, 等. 平面冗余自由度机器人自寻优运动优化方法[J]. 哈尔滨工程大学学报, 2015, 36(4): 528-533.
	Huo Xi-jian, Liu Yi-wei, Jiang Li, et al. Self-optimizing kinematic optimization method of planar redundant robots[J]. Journal of Harbin Engineering University, 2015, 36(4): 528-533.
19	霍希建, 刘伊威, 姜力, 等. 具有关节限位的 7R 仿人机械臂逆运动学优化[J]. 吉林大学学报: 工学版, 2016, 46(1): 213-220.
	Huo Xi-jian, Liu Yi-wei, Jiang Li, et al. Inverse kinematic optimization of 7R humanoid arm with joint limits[J]. Journal of Jilin University: Engineering Edition, 2016, 46(1): 213-220.
20	Kuhlemann I, Schweikard A, Jauer P, et al. Robust inverse kinematics by configuration control for redundant manipulators with seven DoF[C]∥2016 2nd International Conference on Control, Automation and Robotics (ICCAR). Washington, D C, USA, 2016: 49-55.
21	Omisore O M, Han S, Ren L, et al. Deeply-learnt damped least-squares (DL-DLS) method for inverse kinematics of snake-like robots[J]. Neural Networks, 2018, 107: 34-47.
22	Lv X, Tan Z, Chen K, et al. Improved recurrent neural networks for online solution of Moore‐Penrose inverse applied to redundant manipulator kinematic control[J]. Asian Journal of Control, 2020, 22(3): 1188-1196.
23	Dereli S, Köker R. IW-PSO approach to the inverse kinematics problem solution of a 7-DOF serial robot manipulator[J]. International Journal of Natural and Engineering Sciences, 2018, 36(1): 75-85.
24	许杉, 李高峰, 刘景泰, 等. 基于点触任务的可变形臂逆运动学求解[J]. 机器人, 2017, 39(4): 23-32.
	Xu Shan, LI Gao-feng, Liu Jing-tai, et al. Inverse kinematics solution of deformable manipulator for point touching task[J]. Robot, 2017, 39(4): 23-32.

相关文章 15

[1]	谭国金,孔庆雯,何昕,张攀,杨润超,朝阳军,杨忠. 基于动力特性和改进粒子群优化算法的桥梁冲刷深度识别[J]. 吉林大学学报(工学版), 2023, 53(6): 1592-1600.
[2]	孙琪凯,张楠,刘潇,周子骥. 基于Timoshenko梁理论的钢-混组合梁动力折减系数[J]. 吉林大学学报(工学版), 2023, 53(2): 488-495.
[3]	秦静,郑德,裴毅强,吕永,苏庆鹏,王膺博. 基于PSO-GPR的发动机性能与排放预测方法[J]. 吉林大学学报(工学版), 2022, 52(7): 1489-1498.
[4]	朱思峰,赵明阳,柴争义. 边缘计算场景中基于粒子群优化算法的计算卸载[J]. 吉林大学学报(工学版), 2022, 52(11): 2698-2705.
[5]	金顺福,郄修尘,武海星,霍占强. 基于新型休眠模式的云虚拟机分簇调度策略及性能优化[J]. 吉林大学学报(工学版), 2020, 50(1): 237-246.
[6]	王宏志,姜方达,周明月. 基于遗传粒子群优化算法的认知无线电系统功率分配[J]. 吉林大学学报(工学版), 2019, 49(4): 1363-1368.
[7]	陈东良,臧睿,段鹏,赵伟鹏,翁旭涛,孙杨,唐艺鹏. 基于新月鱼尾推进理论的多连杆鱼骨仿生设计[J]. 吉林大学学报(工学版), 2019, 49(4): 1246-1257.
[8]	刘颖, 张凯, 于向军. 基于代理模型的中空轴式大型静压轴承多目标优化[J]. 吉林大学学报(工学版), 2017, 47(4): 1130-1137.
[9]	黄璇, 郭立红, 李姜, 于洋. 改进粒子群优化BP神经网络的目标威胁估计[J]. 吉林大学学报(工学版), 2017, 47(3): 996-1002.
[10]	张家旭, 李静. 基于混合优化方法的UniTire轮胎模型参数辨识[J]. 吉林大学学报(工学版), 2017, 47(1): 15-20.
[11]	卢英, 王慧琴, 秦立科. 高大空间建筑火灾精确定位方法[J]. 吉林大学学报(工学版), 2016, 46(6): 2067-2073.
[12]	祁若龙, 张伟, 王铁军, 李正. 仿人头颈部机器人跟踪运动控制[J]. 吉林大学学报(工学版), 2016, 46(5): 1595-1601.
[13]	邵鹏, 吴志健, 周炫余. 基于反向学习的粒子群算法对线性相位低通FIR滤波器的优化[J]. 吉林大学学报(工学版), 2015, 45(3): 907-912.
[14]	邱宁佳, 隋振, 李明哲, 郑承香. 六自由度机器人空间划线轨迹规划算法[J]. 吉林大学学报(工学版), 2013, 43(05): 1307-1313.
[15]	孔英秀, 赵丁选, 杨彬, 李天宇, 韩京元. 基于PSO-DE和LMI的鲁棒静态输出反馈控制[J]. 吉林大学学报(工学版), 2013, 43(05): 1375-1380.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

组别	关节1	关节2	关节3	关节4	关节5	关节6	关节7
1	92.96	10.39	0	72.92	-124.34	76.96	121.35
2	92.96	10.39	0	72.92	55.66	-76.96	-58.65
3	92.96	10.39	-180	-72.92	55.66	76.96	121.35
4	-87.04	-10.39	-180	72.92	-124.34	76.96	121.35
5	92.96	10.39	-180	-72.92	-124.34	-76.96	-58.65
6	-87.04	-10.39	0	-72.92	55.66	76.96	121.35
7	-87.04	-10.39	-180	72.92	55.66	-76.96	-58.65
8	-87.04	-10.39	0	-72.92	-124.34	-76.96	-58.65

算法	计算时间/ms	平均目标函数值	平均位置误差/10^-7 m
本文	11.26	4.6	7.5
文献［17］	10.39	8.9	8.4