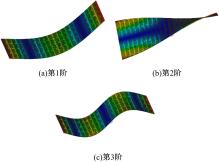
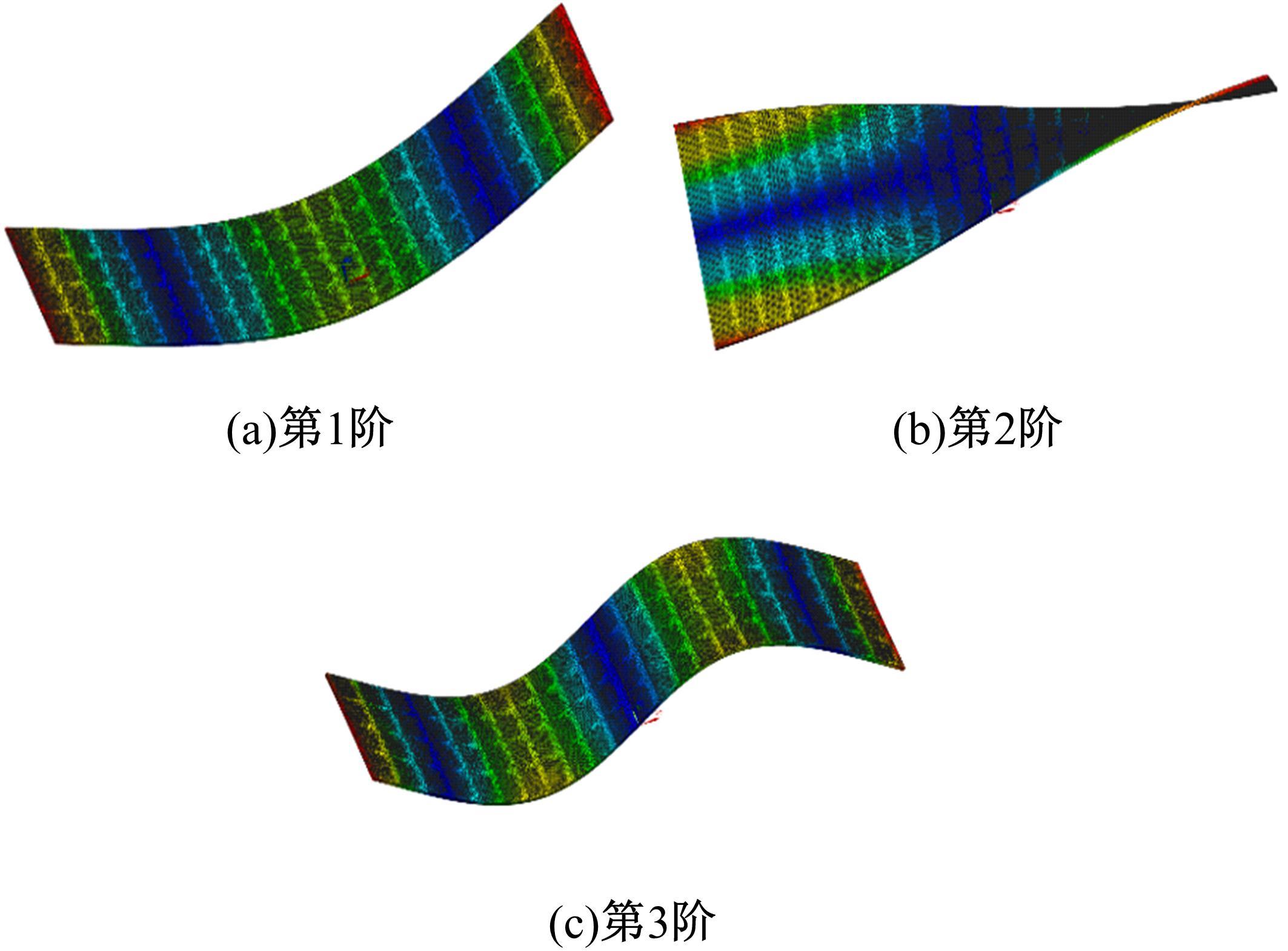
吉林大学学报(工学版) ›› 2023, Vol. 53 ›› Issue (9): 2676-2685.doi: 10.13229/j.cnki.jdxbgxb.20211295
基于Lyapunov理论的卫星大挠性太阳能帆板分布式自适应振动抑制控制方法
- 吉林大学 仪器科学与电气工程学院,长春 130012
Distributed adaptive vibration suppression control method of large solar panels for satellites based on Lyapunov theory
Liu ZHANG( ),Qing-ming ZENG,Huan-yu ZHAO(
),Qing-ming ZENG,Huan-yu ZHAO( ),Guo-wei FAN
),Guo-wei FAN
- College of Instrumentation & Electrical Engineering,Jilin University,Changchun 130012,China
摘要:
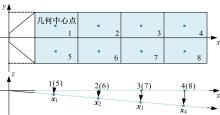
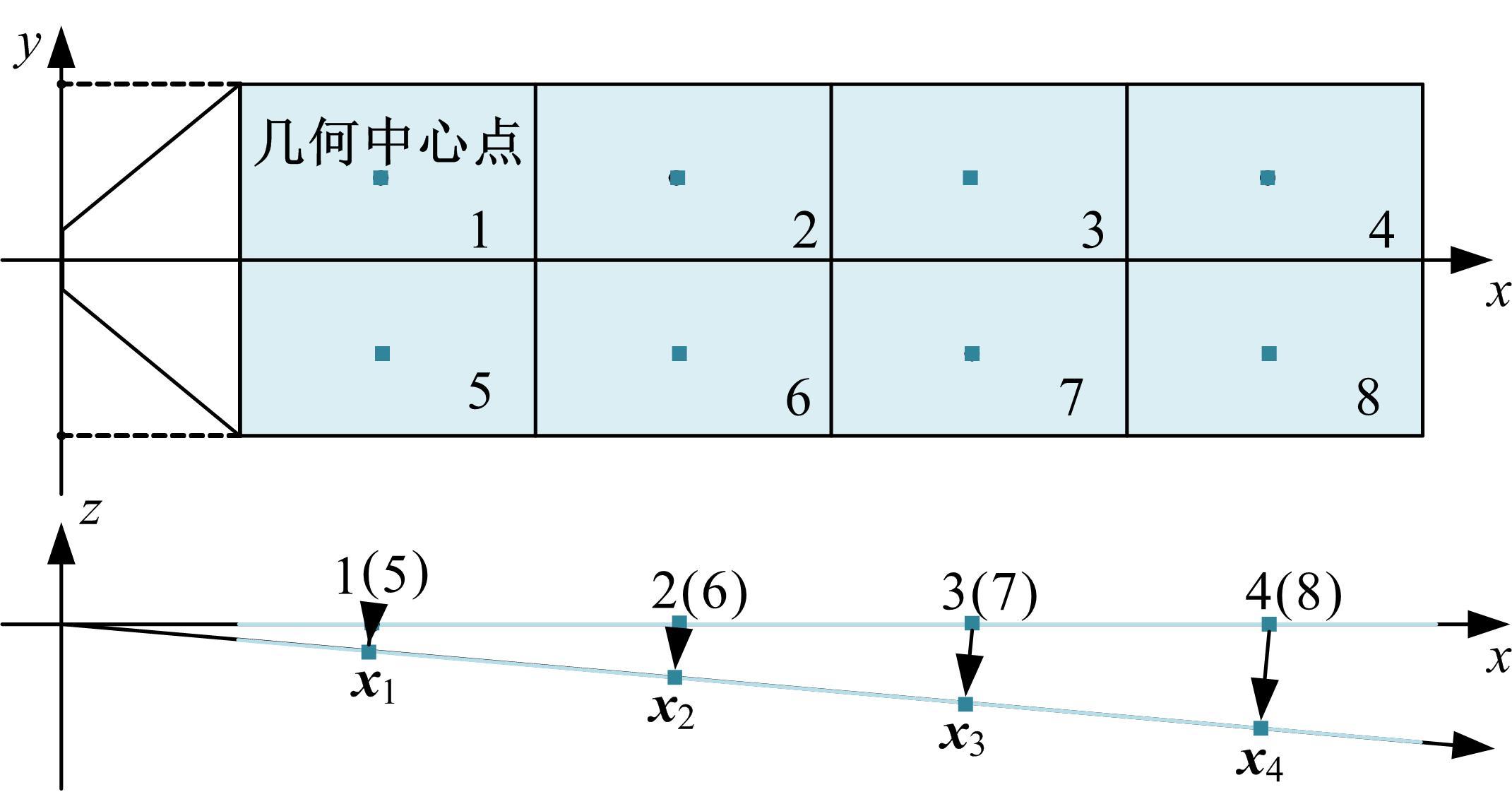
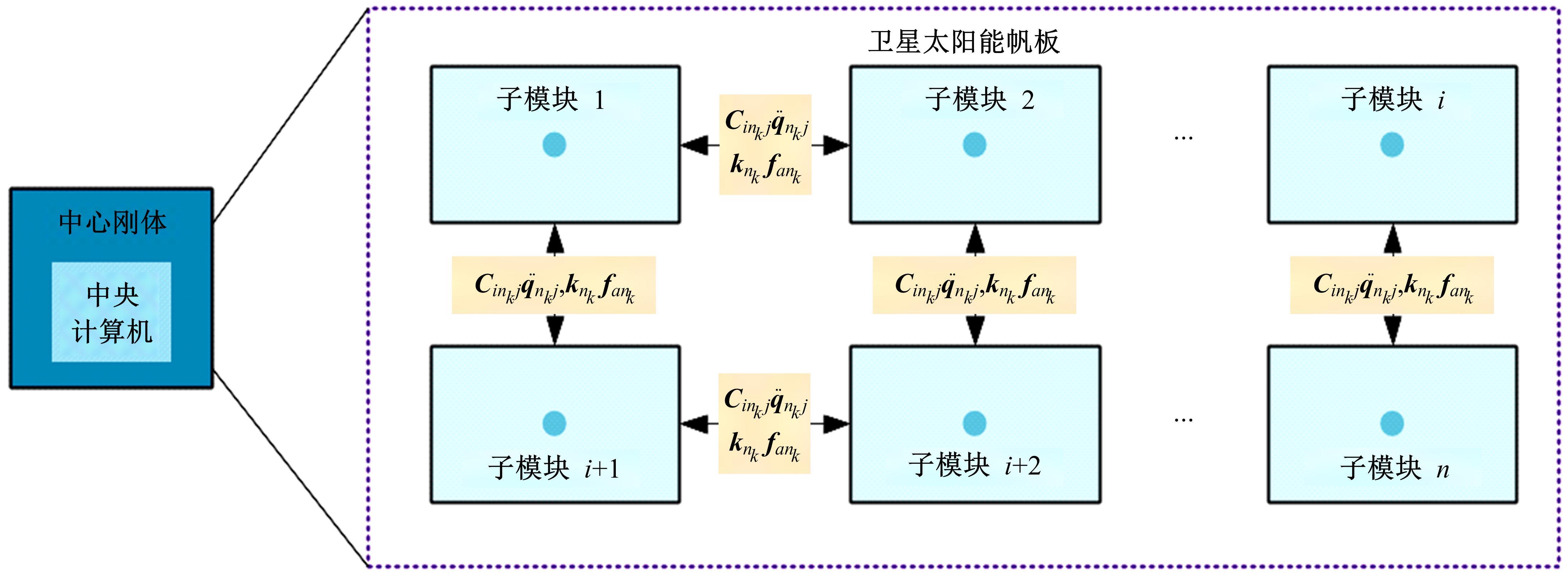
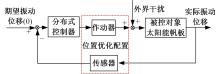
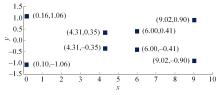
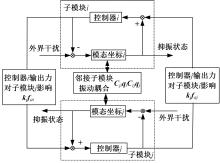
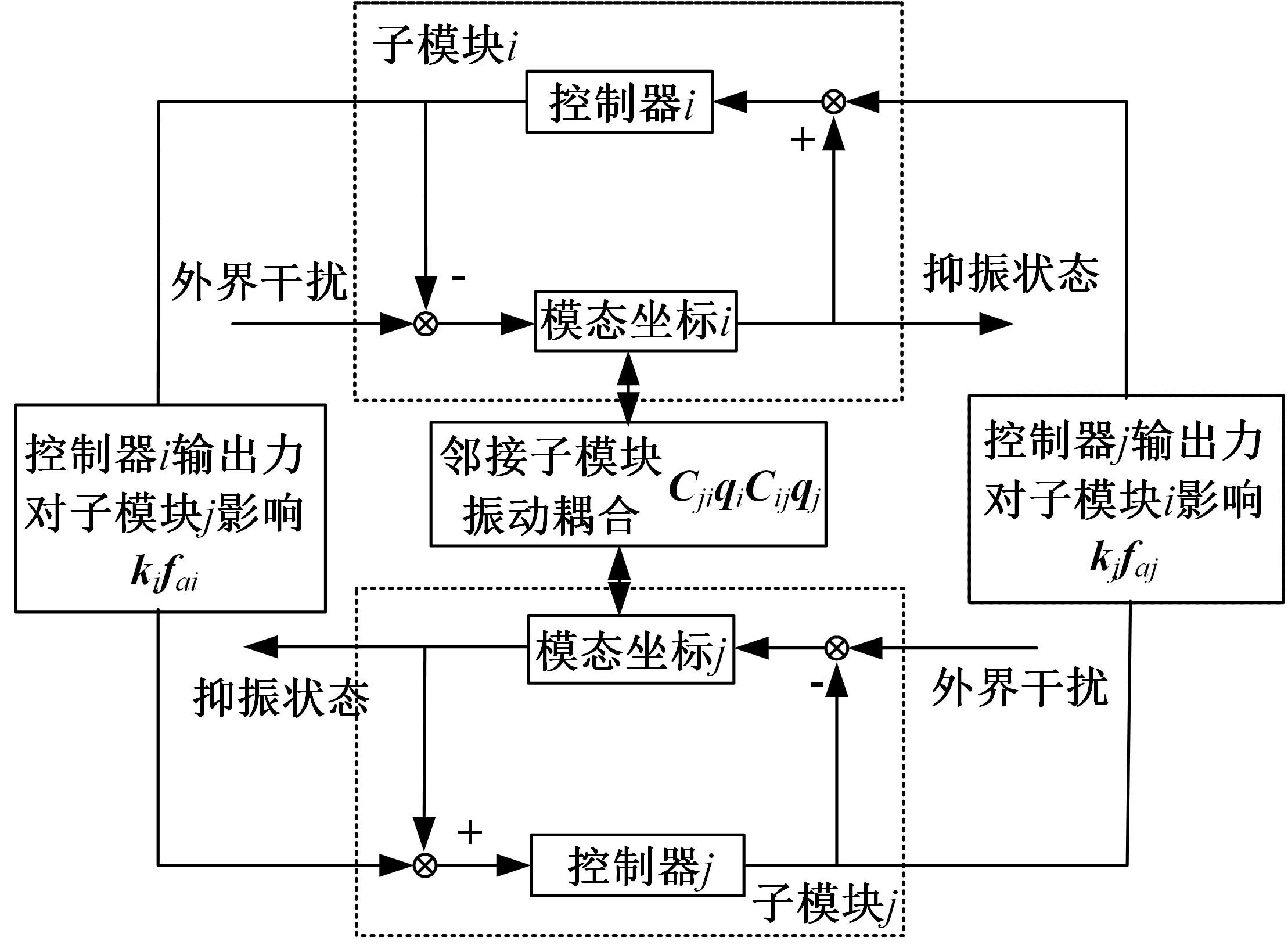
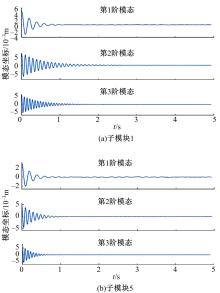
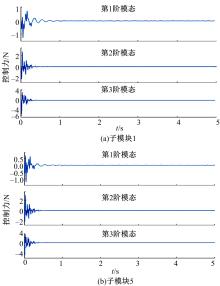
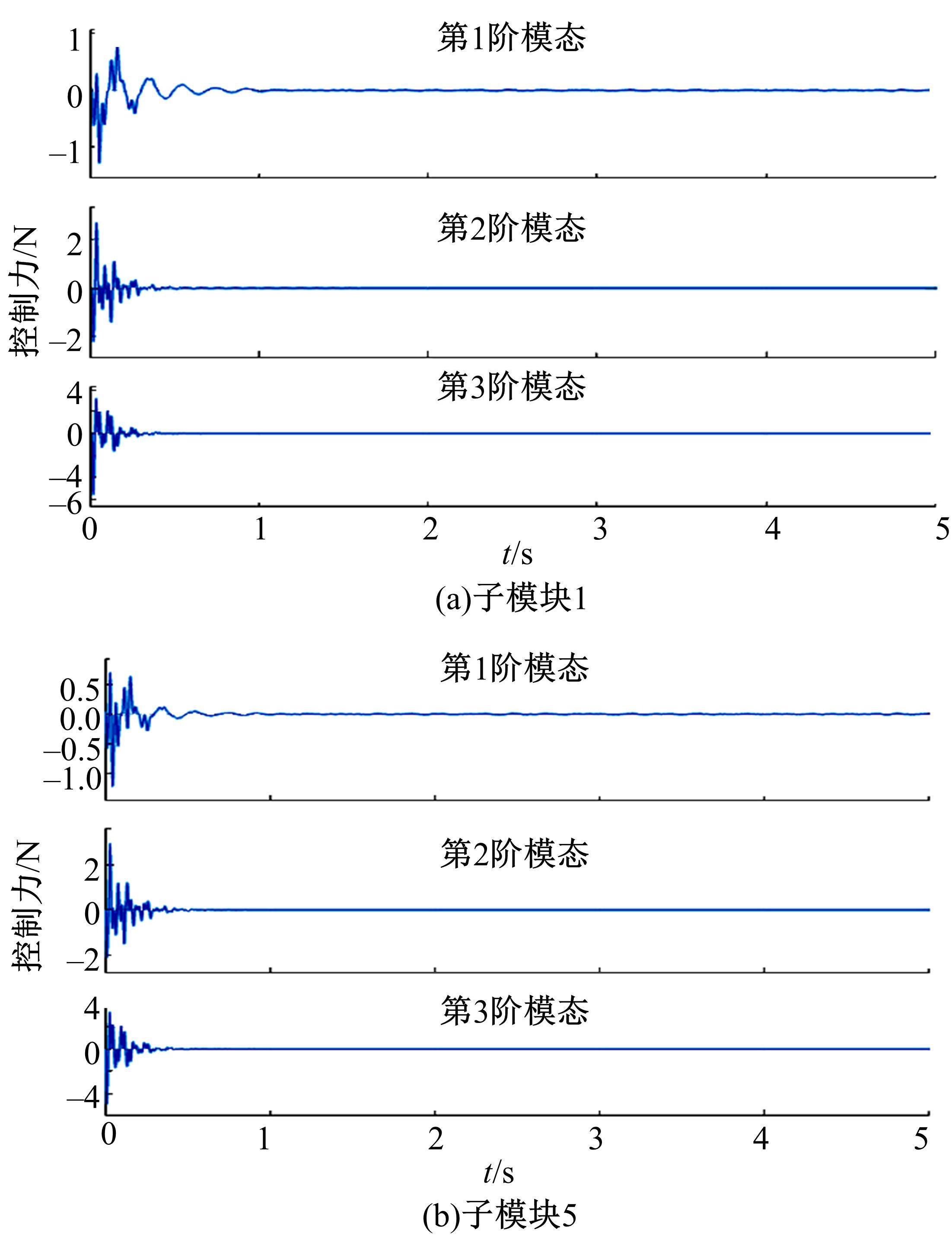
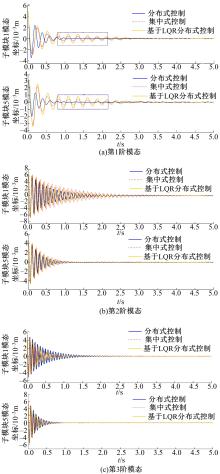
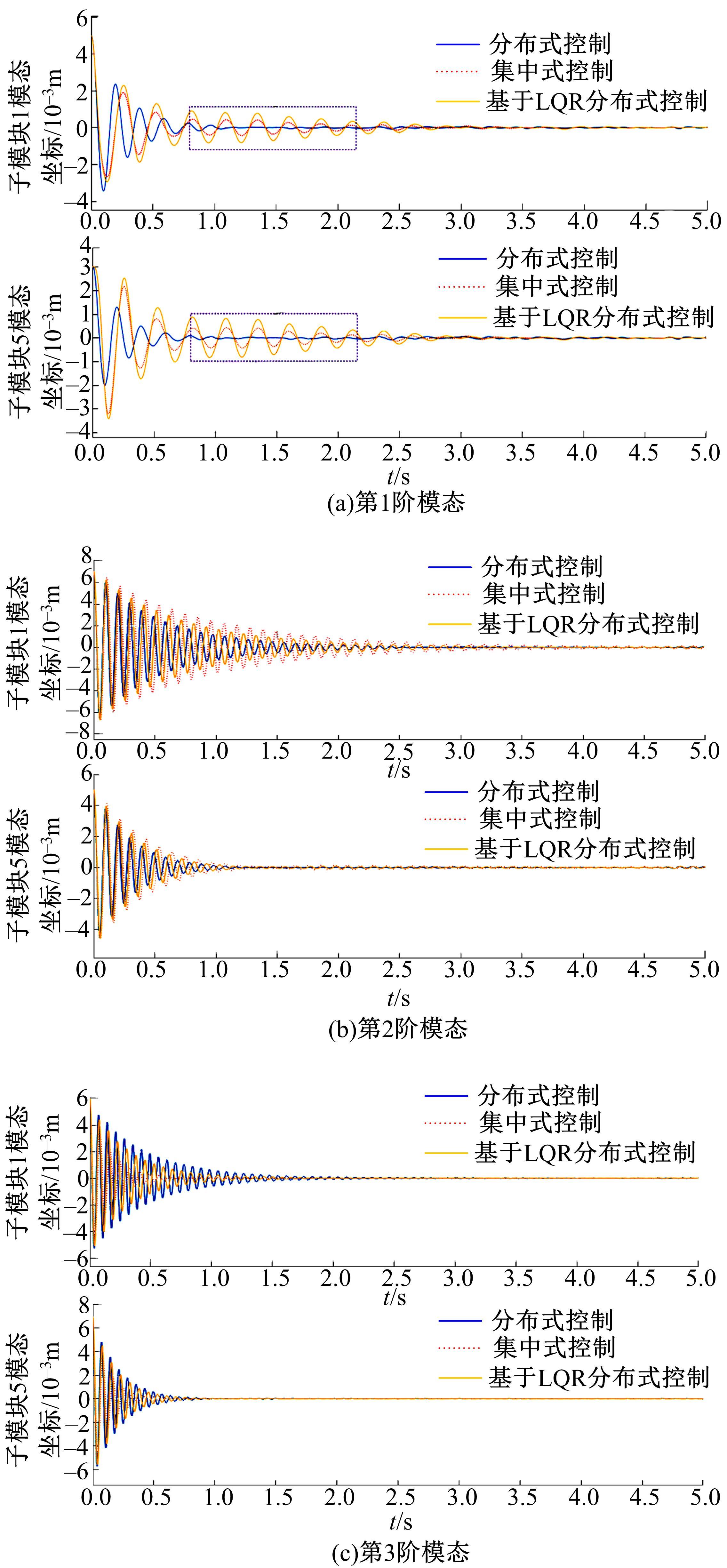
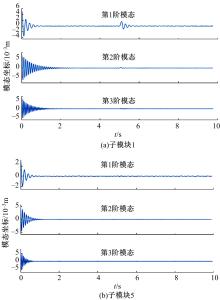
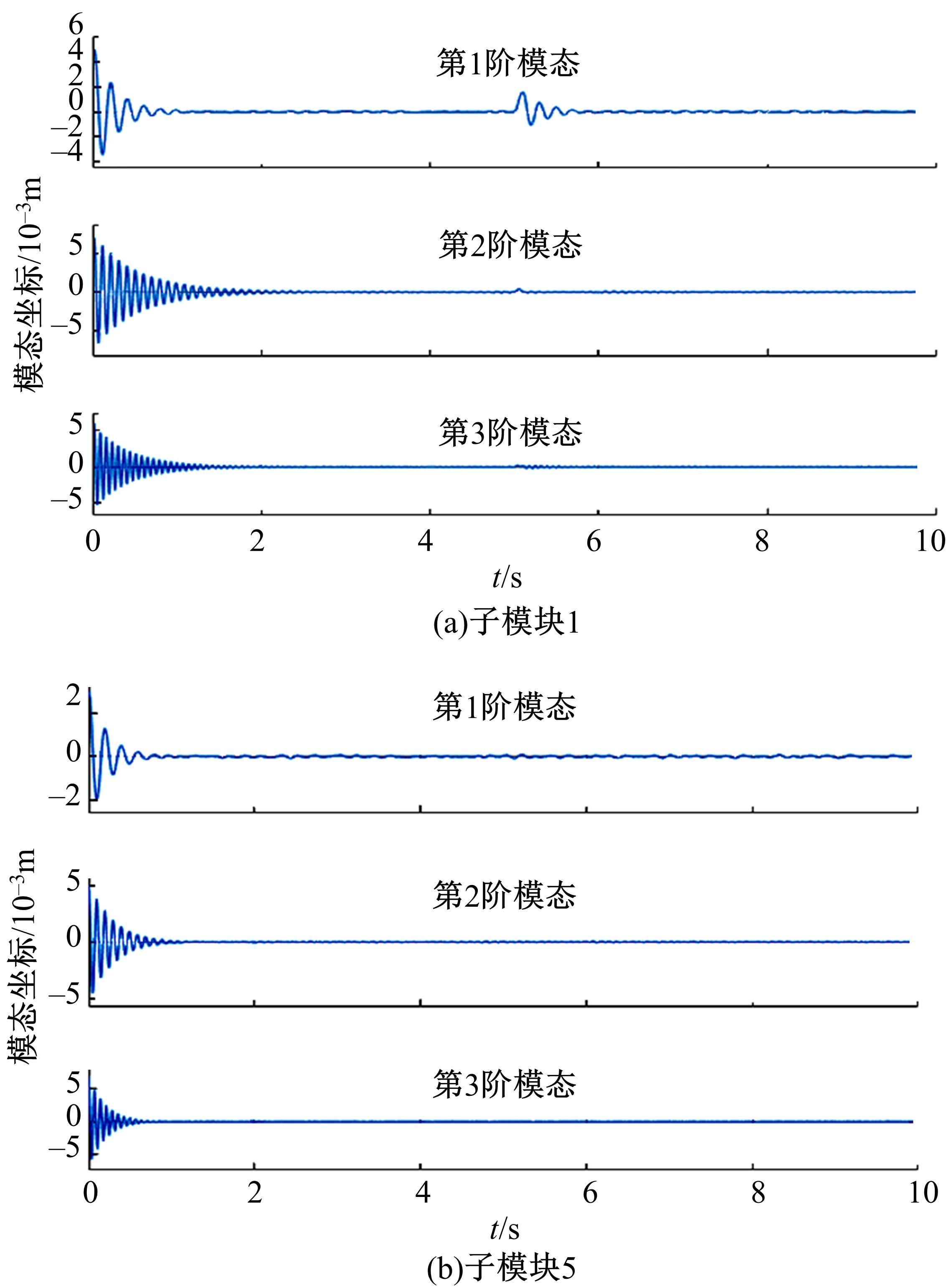
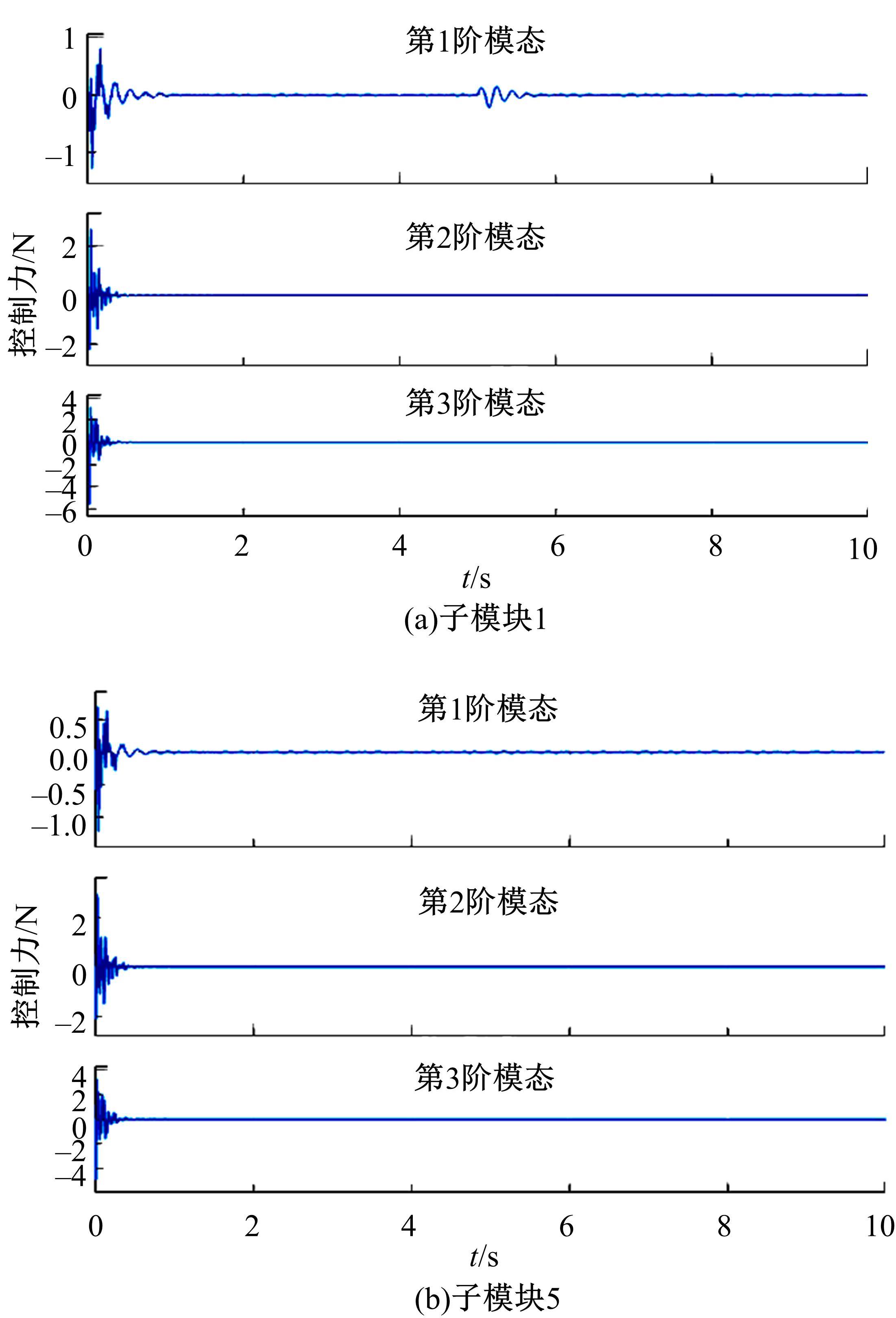
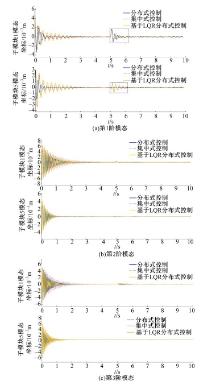
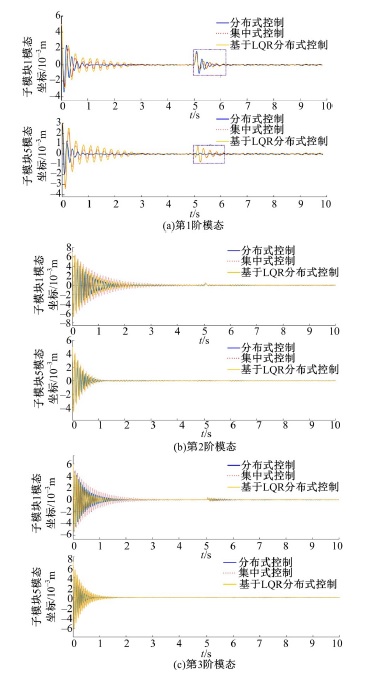
提出了一种分布式自适应振动抑制控制方法,有效抑制了卫星大挠性帆板在轨振动问题。考虑作动器和传感器的安装位置对控制效果的影响,通过分析邻接子模块之间振动和输出力的耦合影响,基于Lyapunov理论设计了完整的分布式自适应控制器。仿真结果表明,在外界持续干扰等情况下,本文设计的分布式控制系统与基于线性二次型调节器(LQR)的分布式控制方法相比抑振时间缩短了40%,与集中式控制方法相比抑振时间缩短了50%,得到了更良好的在轨抑振效果,对于卫星的稳定运行具有重要意义。
中图分类号:
- V448.22
| 1 | Nadafi R, Kabganian M, Kamali A, et al. Super-twisting sliding mode control design based on Lyapunov criteria for attitude tracking control and vibration suppression of a flexible spacecraft[J]. Measurement and Control, 2019, 52(7/8): 814-831. |
| 2 | Liu Feng, Yue Bao-zeng, Zhao Liang-yu. Attitude dynamics and control of spacecraft with a partially filled liquid tank and flexible panels[J]. Acta Astronautica, 2018, 143: 327-336. |
| 3 | Yuan Q, Liu Y, Qi N. Active vibration suppression for maneuvering spacecraft with high flexible appendages[J]. Acta Astronautica, 2017, 139: 512-520. |
| 4 | Luo Y J, Xu M L, Yan B, et al. PD control for vibration attenuation in Hoop truss structure based on a novel piezoelectric bending actuator[J]. Journal of Sound & Vibration, 2015, 339: 11-24. |
| 5 | Wang Z, Xu M, Jia Y, et al. Vibration suppression-based attitude control for flexible spacecraft[J]. Aerospace Science & Technology, 2017, 70: 487-496. |
| 6 | Rahman N U, Alam M N, Ansari J A. An experimental study on dynamic analysis and active vibration control of smart laminated plates[J]. Materials Today: Proceedings, 2021, 46: 9550-9554. |
| 7 | Tian J, Guo Q, Shi G. Laminated piezoelectric beam element for dynamic analysis of piezolaminated smart beams and GA-based LQR active vibration control[J]. Composite Structures, 2020, 252: No.112480. |
| 8 | Hu Q, Ma G, Li C. Active vibration control of a flexible plate structure using LMI-based H∞ output feedback control law[C]∥Fifth World Congress on Intelligent Control and Automation, Hangzhou, China, 2004: No.8369247. |
| 9 | 苗双全, 丛炳龙, 刘向东. 基于输入成形的挠性航天器自适应滑模控制[J]. 航空学报, 2013, 34(8): 1906-1914. |
| Miao Shuang-quan, Cong Bing-long, Liu Xiang-dong. Adaptive sliding mode control of flexible spacecraft on input shaping[J]. Acta Aeronautica Et Astronautica Sinica, 2013, 34(8): 1906-1914. | |
| 10 | Wang E, Wu S, Liu Y, et al. Distributed vibration control of a large solar power satellite[J]. Astrodynamics, 2019, 3(2): 189-203. |
| 11 | Ji N, Liu J. Distributed vibration control for flexible spacecraft with distributed disturbance and actuator fault[J]. Journal of Sound and Vibration, 2020, 475: No.5274. |
| 12 | Li Q, Yang H, Zhao D, et al. Fault-tolerant control and vibration suppression of flexible spacecraft: An interconnected system approach[J]. Chinese Journal of Aeronautics, 2020, 33(7): 2014-2023. |
| 13 | Nakka Y, Chung S J, Allison J, et al. Nonlinear attitude control of a spacecraft with distributed actuation of solar arrays[J]. Journal of Guidance, Control, and Dynamics, 2019, 42(3): 458-475. |
| 14 | Chen T, Shan J, Wen H. Distributed passivity-based control for multiple flexible spacecraft with attitude-only measurements[J]. Aerospace Science and Technology, 2019, 94: No.105408. |
| 15 | 韩泽强. 大挠性卫星高精度控制关键技术研究[D]. 哈尔滨:哈尔滨工业大学航天学院,2020. |
| Han Ze-qiang. Research on key technologies of high-precision satellite high-precision control[D]. Harbin: School of Astronautics, Harbin Institute of Technology, 2020. | |
| 16 | Muhammad A K, Wang X G, Cui N G, et al. A criterion for optimal sensor placement for minimizing spillover effects on optimal controllers[J]. Journal of Vibration and Control, 2018, 24(8): 1469-1487. |
| 17 | 刘潇翔, 石恒, 王思野. 挠性空间结构的密集模态特性及影响分析[J].空间控制技术与应用,2017,43(01):11-16. |
| Liu Xiao-xiang, Shi Heng, Wang Si-ye. An analysis on characteristics and impacts of close modes in flexible space structures[J]. Aerospace Control and Application, 2017, 43(1): 11-16. | |
| 18 | Åström K J, Murray R M. Feedback Systems: An Introduction for Scientists and Engineers[M]. Princeton: Princeton University Press, 2010. |
| 19 | He W, Ge S Z S. Dynamic modeling and vibration control of a flexible satellite[J]. IEEE Transactions on Aerospace & Electronic Systems, 2015, 51(2): 1422-1431. |
| 20 | 陆栋宁, 刘一武. 带旋转挠性太阳帆板卫星自适应控制[J]. 航天控制, 2014, 32(1): 49-54. |
| Lu Dong-ning, Liu Yi-wu. Adaptive control of the spacecraft with a rotating flexible solar array[J]. Aerospace Control, 2014, 32(1): 49-54. |
| [1] | 何德峰,周丹,罗捷. 跟随式车辆队列高效协同弦稳定预测控制[J]. 吉林大学学报(工学版), 2023, 53(3): 726-734. |
| [2] | 刘岩,丁天威,王宇鹏,都京,赵洪辉. 基于自适应控制的燃料电池发动机热管理策略[J]. 吉林大学学报(工学版), 2022, 52(9): 2168-2174. |
| [3] | 张冲,胡云峰,宫洵,孙耀. 燃料电池阴极流量无模型自适应滑模控制器设计[J]. 吉林大学学报(工学版), 2022, 52(9): 2085-2095. |
| [4] | 谭永营,伊善贞,薛大兵,王晓明,袁磊. 负载型四足步行平台对角步态重量自适应行走控制[J]. 吉林大学学报(工学版), 2021, 51(4): 1506-1517. |
| [5] | 刘明,荣学文,李贻斌,张帅帅,尹燕芳,阮久宏. 基于地形聚类分析的移动机器人速度自适应控制[J]. 吉林大学学报(工学版), 2021, 51(4): 1496-1505. |
| [6] | 周挺,徐宇工,吴斌. 球形机器人的自适应分数阶PIλDμ滑模速度控制方法[J]. 吉林大学学报(工学版), 2021, 51(2): 728-737. |
| [7] | 马彦,黄健飞,赵海艳. 基于车间通信的车辆编队控制方法设计[J]. 吉林大学学报(工学版), 2020, 50(2): 711-718. |
| [8] | 顾万里,王萍,胡云峰,蔡硕,陈虹. 具有H∞性能的轮式移动机器人非线性控制器设计[J]. 吉林大学学报(工学版), 2018, 48(6): 1811-1819. |
| [9] | 李志慧, 夏英集, 曲昭伟, 任景琛. 视频监控的数据驱动背景模型[J]. 吉林大学学报(工学版), 2017, 47(4): 1286-1294. |
| [10] | 邵克勇, 陈丰, 王婷婷, 王季驰, 周立朋. 无平衡点分数阶混沌系统全状态自适应控制[J]. 吉林大学学报(工学版), 2017, 47(4): 1225-1230. |
| [11] | 李兵强, 陈晓雷, 林辉, 吕帅帅, 马冬麒. 机电伺服系统高精度自适应反推滑模控制[J]. 吉林大学学报(工学版), 2016, 46(6): 2003-2009. |
| [12] | 曹福成, 邢笑雪, 李元春, 赵希禄. 下肢康复机器人轨迹自适应滑模阻抗控制[J]. 吉林大学学报(工学版), 2016, 46(5): 1602-1608. |
| [13] | 黄晶莹, 秦大同, 刘永刚. 基于自适应滤波的电动汽车电-液复合制动系统防抱死控制[J]. 吉林大学学报(工学版), 2016, 46(4): 1044-1051. |
| [14] | 吴爱国, 杨硕, 张涵, 李长滨. 压机的调平和跟踪控制[J]. 吉林大学学报(工学版), 2014, 44(4): 1051-1056. |
| [15] | 胡立坤,马文光,赵鹏飞,卢子广. 六自由度机械臂的非奇异快速终端滑模控制[J]. 吉林大学学报(工学版), 2014, 44(3): 735-741. |
|