基于Timoshenko梁理论的钢-混组合梁动力折减系数

doi:10.13229/j.cnki.jdxbgxb20210742

摘要/Abstract

摘要：

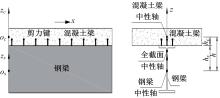
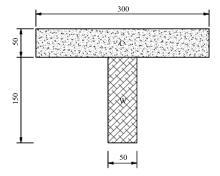
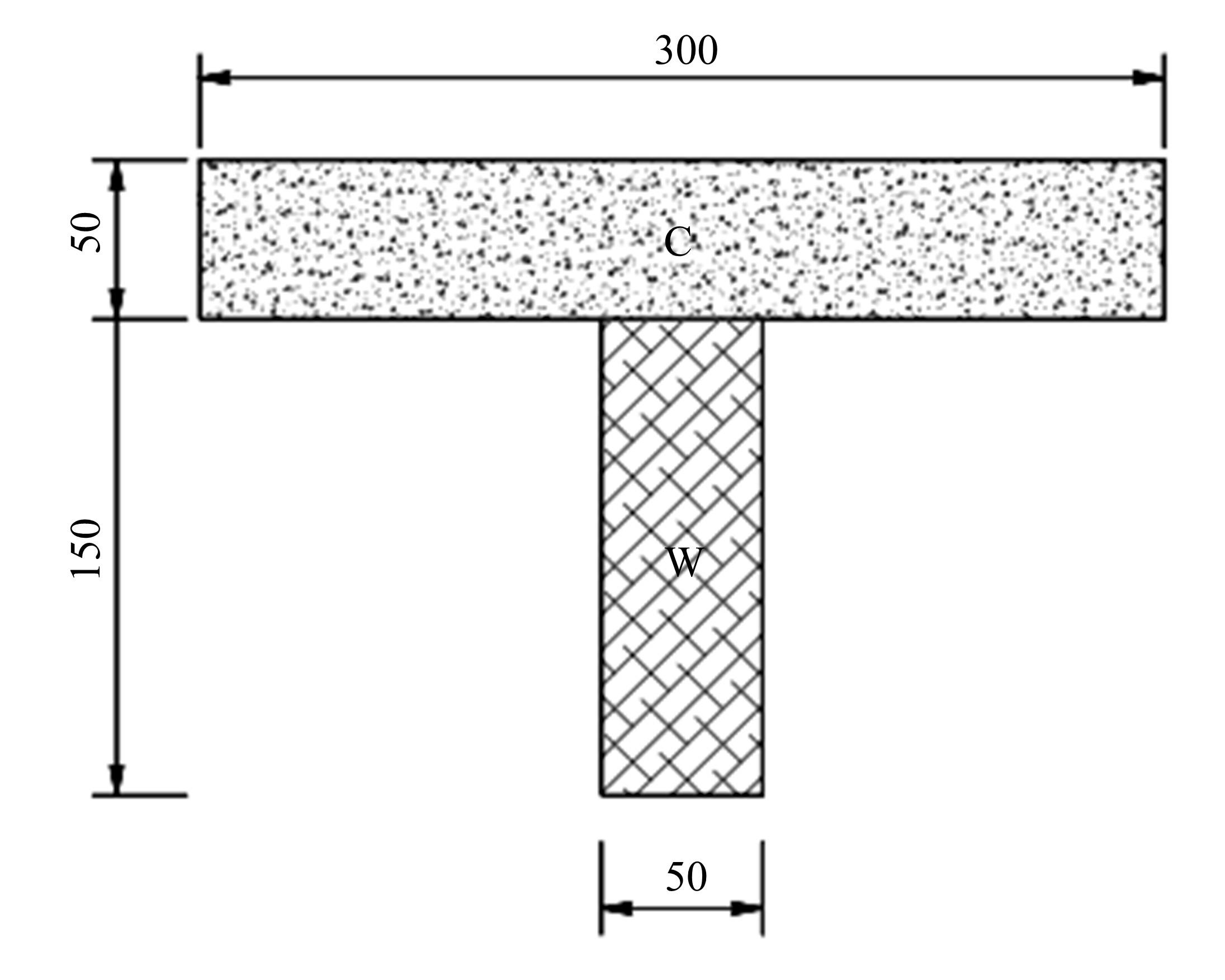
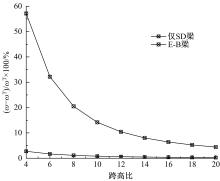
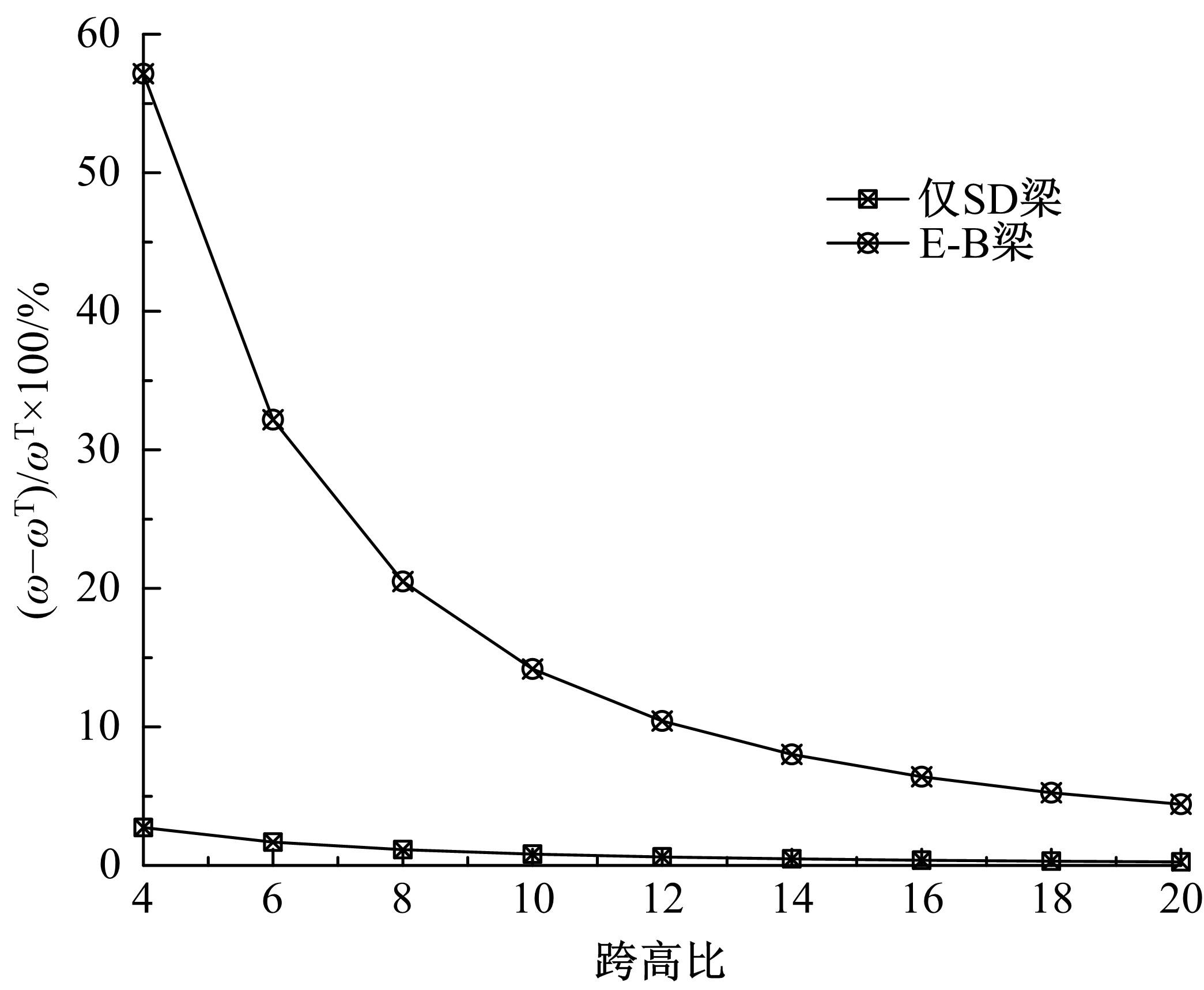
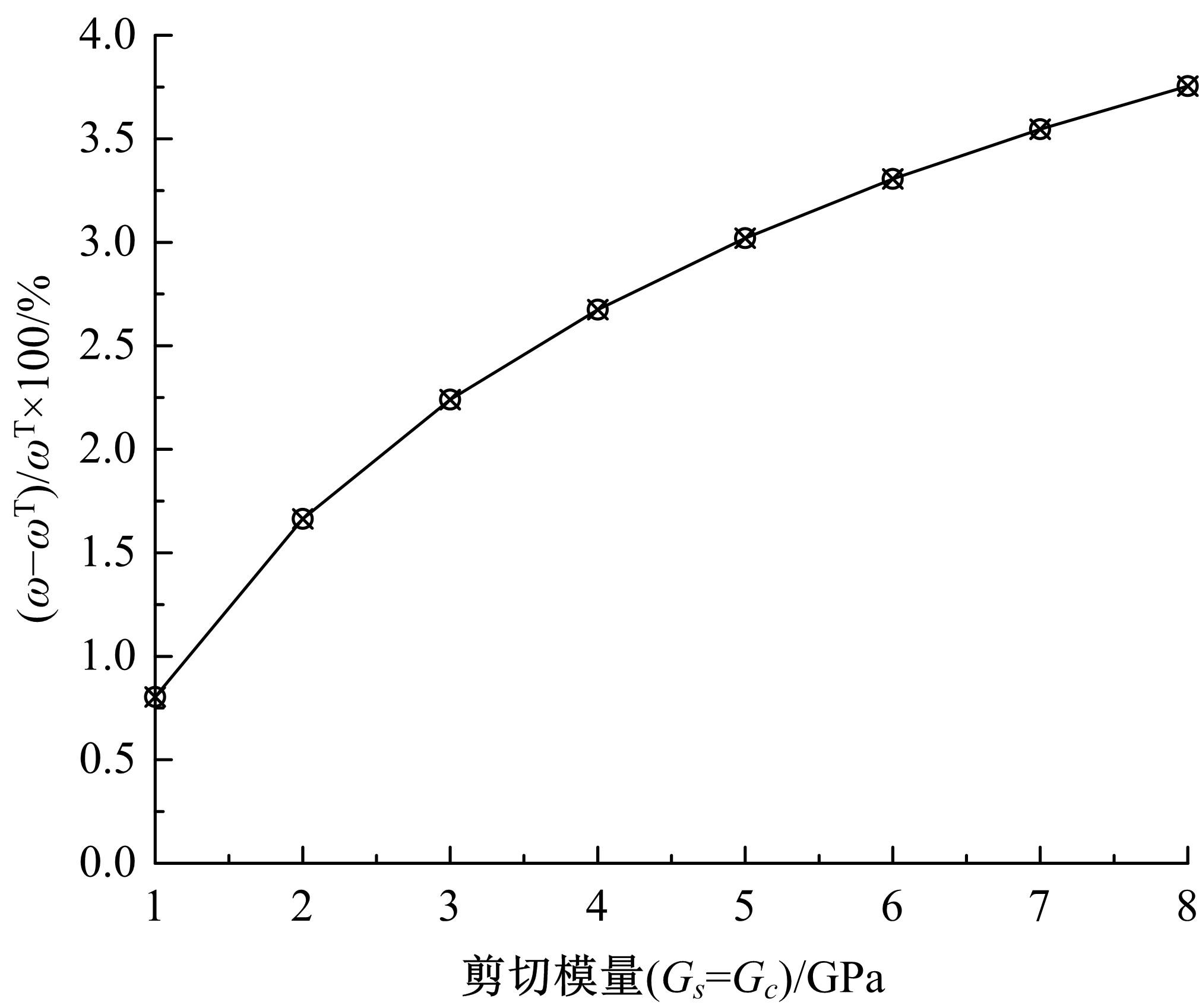
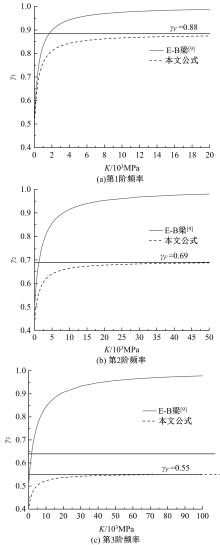
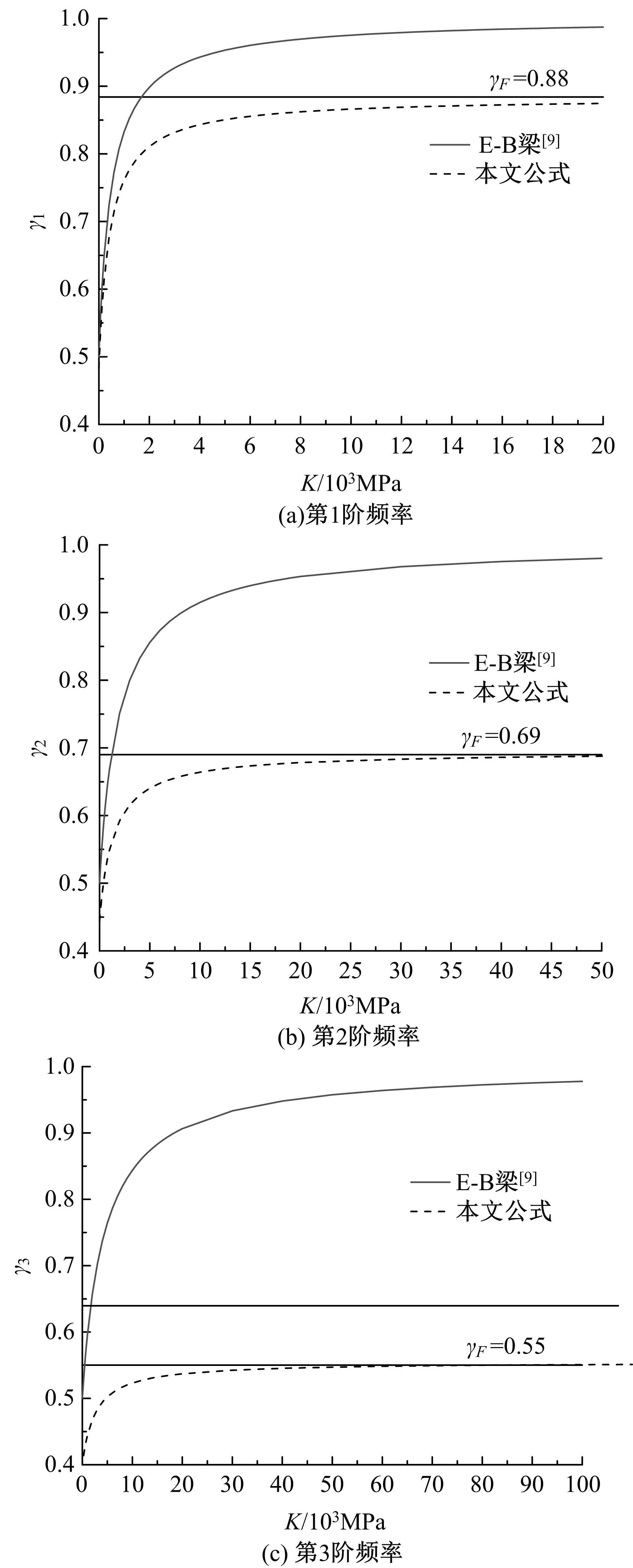
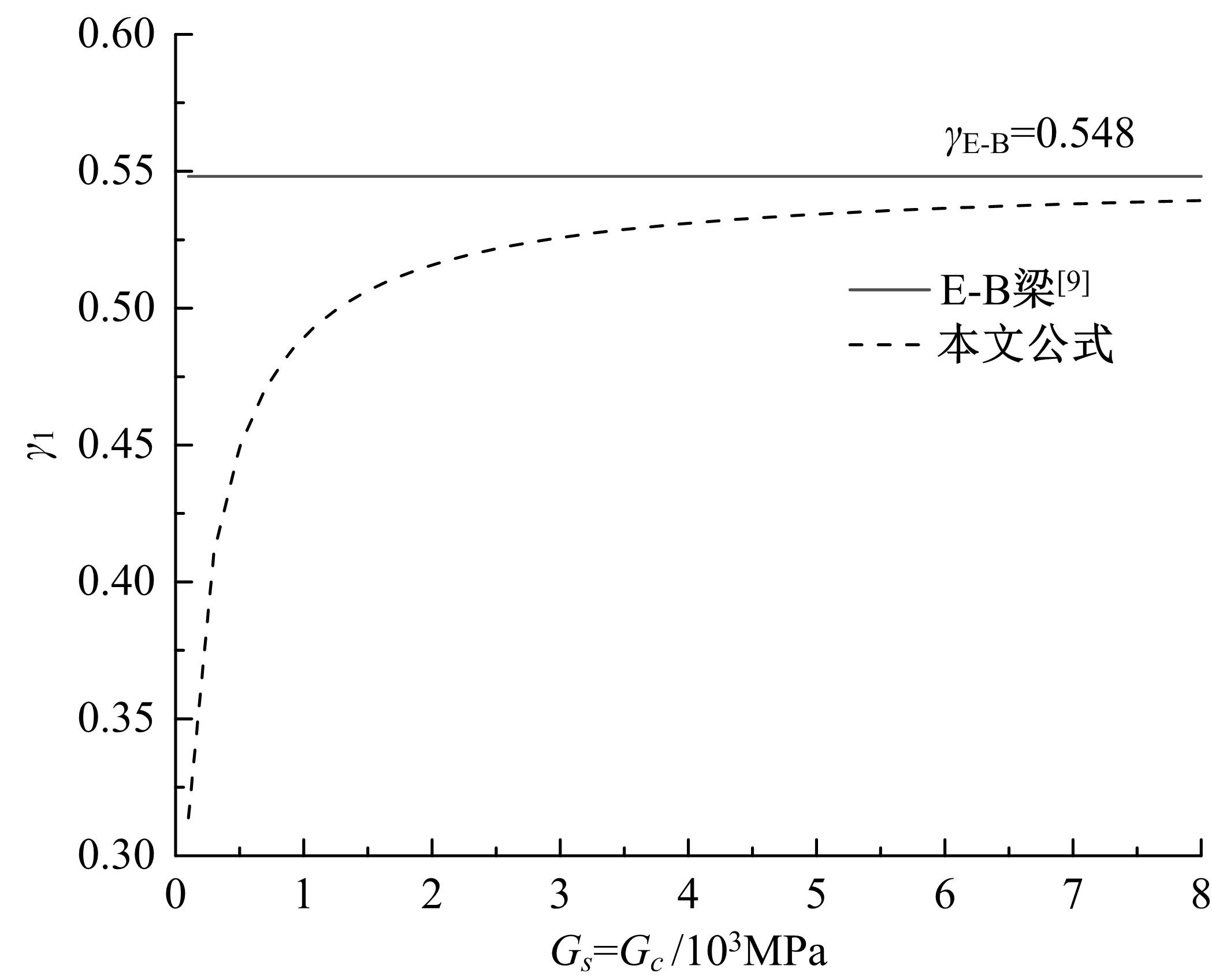
基于Timoshenko梁理论，推导了考虑剪切滑移影响的钢-混组合梁的运动微分方程，得到了简支钢-混组合梁的自振频率和振型的显式解析表达式。提出了更适用于钢-混组合梁动力分析的动力折减系数，并给出了“刚度折减系数”和“频率折减系数”的解析表达式。与已有基于Euler-Bernoulli梁理论的动力折减系数进行了对比分析，讨论了剪力键刚度、剪切变形、转动惯量、跨高比对频率折减系数的影响。结果表明：当进行钢-混组合梁动力分析时，尤其是跨高比较小的组合梁，可以忽略转动惯量的影响，但不可忽略剪切变形的影响。

关键词: 桥梁工程, 钢-混组合梁, 动力折减系数, 剪切变形, 界面剪切滑移, 解析解

Abstract:

The motion differential equation of steel-concrete composite beams considering the shear slip effect was derived based on the Timoshenko beam theory. And the analytical expressions of eigenfrequencies and modes for simply-supported steel-concrete composite beams were obtained. The dynamic reduction coefficients which were more suitable for dynamic analysis of steel-concrete composite beams were proposed， and the analytical expressions of "stiffness reduction coefficient" and "frequency reduction coefficient" were given. Then the dynamic reduction coefficients were compared with the existing one based on Euler-Bernoulli beam theory. The effects of shear connector stiffness， shear deformation， rotary inertia， and span-to-depth ratio on the frequency reduction coefficient were discussed. The results show that the effect of the rotary inertia can be ignored， but that of the shear deformation must be considered in the dynamic analysis of steel-concrete composite beams with smaller span-to-depth ratios.

Key words: bridge engineering, steel-concrete composite beam, dynamic reduction coefficient, shear deformation, shear slip, analytical expression

中图分类号:

U441

孙琪凯,张楠,刘潇,周子骥. 基于Timoshenko梁理论的钢-混组合梁动力折减系数[J]. 吉林大学学报(工学版), 2023, 53(2): 488-495.

Qi-kai SUN,Nan ZHANG,Xiao LIU,Zi-ji ZHOU. Dynamic reduction coefficients of steel⁃concrete composite beam based on Timoshenko beam theory[J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(2): 488-495.

图/表 8

图1

图2

表1

图3

图4

图5

图6

表2

钢-混组合梁自振特性对比表"

阶次	实测值	ANSYS	文献［9］模型		本文模型
阶次	实测值	ANSYS	$f n E B$	$γ n E B$	$f n T$	$γ n T$
1	19.38	21.08	22.27	0.88	21.28	0.84
2	63.13	62.48	75.96	0.75	67.02	0.66
3	-	114.48	156.09	0.69	126.07	0.56

表2

参考文献 18

1	聂建国,余志武. 钢-混凝土组合梁在我国的研究及应用[J]. 土木工程学报, 1999, 32(2): 3-8.
	Nie Jian-guo, Yu Zhi-wu. Research and practice of composite steel-concrete beams in China[J]. China Civil Engineering Journal, 1999, 32(2): 3-8.
2	聂建国, 陶慕轩, 吴丽丽, 等. 钢-混凝土组合结构桥梁研究新进展[J]. 土木工程学报, 2012, 45(6): 110-122.
	Nie Jian-guo, Tao Mu-xuan, Wu Li-li,et al.Advances of research on steel-concrete composite bridges[J]. China Civil Engineering Journal, 2012, 45(6): 110-122.
3	刘永健,刘江.钢-混凝土组合梁桥温度作用与效应综述[J]. 交通运输工程学报, 2020, 20(1): 42-59.
	Liu Yong-jian, Liu Jiang. Review on temperature action and effect of steel-concrete composite girder bridge[J]. Journal of Traffic and Transportation Engineering, 2020, 20(1): 42-59.
4	聂建国,沈聚敏,余志武. 考虑滑移效应的钢-混凝土组合梁变形计算的折减刚度法[J]. 土木工程学报, 1995, 28(6): 11-17.
	Nie Jian-guo, Shen Ju-min, Yu Zhi-wu. A reduced rigidity method for calculating deformation of composite steel-concrete beams[J]. China Civil Engineering Journal, 1995, 28(6): 11-17.
5	王景全,吕志涛,刘钊. 部分剪力连接钢-混凝土组合梁变形计算的组合系数法[J]. 东南大学学报: 自然科学版, 2005, 35(): 5-10.
	Wang Jing-quan, Lv Zhi-tao, Liu Zhao. Consistency factor method for calculating deformation of composite steel-concrete girders with partial shear connection[J]. Journal of Southeast University (Natural Science Edition), 2005, 35(S1): 5-10.
6	徐荣桥,陈德权.组合梁挠度计算的改进折减刚度法[J]. 工程力学,2013, 30(2): 285-291.
	Xu Rong-qiao, Chen De-quan. Modified reduced stiffness method for calculating the deflection of composite beams[J]. Engineering Mechanics, 2013, 30(2): 285-291.
7	张云龙, 刘占莹, 吴春利, 等. 钢-混凝土组合梁静动力响应[J]. 吉林大学学报: 工学版, 2017, 47(3): 789-795.
	Zhang Yun-long, Liu Zhan-ying, Wu Chun-li,et al. Static and dynamic responses of steel-concrete composite beams[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(3): 789-795.
8	侯忠明,夏禾,张彦玲. 栓钉连接件抗剪刚度对钢-混凝土结合梁自振特性影响研究[J].中国铁道科学, 2012, 33(6): 24-29.
	Hou Zhong-ming, Xia He, Zhang Yan-ling. The influence of the shear stiffness of stud connectors on the natural vibration characteristics of steel-concrete composite beams[J]. China Railway Science, 2012, 33(6): 24-29.
9	侯忠明,夏禾,王元清,等. 钢-混凝土组合梁动力折减系数研究[J]. 振动与冲击, 2015, 34(4): 74-81.
	Hou Zhong-ming, Xia He, Wang Yuan-qing, et al. Dynamic redution coefficients for a steel-concrete composite beam[J]. Journal of Vibration and Shock, 2015, 34(4): 74-81.
10	张云龙, 郭阳阳, 王静, 等. 钢-混组合梁的固有频率及其振型[J]. 吉林大学学报: 工学版, 2020, 50(2): 581-588.
	Zhang Yun-long, Guo Yang-yang, Wang Jing,et al. Natural frequency and mode of vibration of steel-concrete composite beams[J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(2): 581-588.
11	孙琪凯, 张楠, 刘潇, 等. 基于能量法分析考虑纵向刚度分布的钢-混组合梁自振特性[J]. 振动与冲击, 2021, 40(10): 67-72.
	Sun Qi-kai, Zhang Nan, Liu Xiao, et al. Free vibration characteristics of steel-concrete composite beams considering longitudinal stiffness distribution based on energy method[J]. Journal of Vibration and Shock, 2021, 40(10): 67-72.
12	Sun Q K, Zhang N, Liu X, et al. Free vibrations of steel-concrete composite beams by the dynamic direct stiffness method[J]. International Journal of Structural Stability and Dynamic, 2021, 21(4): 2150049.
13	Berczyński S, Wróblewski T. Vibration of steel-concrete composite beams using the Timoshenko beam model[J]. Journal of Vibration and Control, 2005, 11(6): 829-848.
14	Xu R Q, Wu Y F. Static dynamic and buckling analysis of partial interaction composite members using Timoshenko's beam theory[J]. International Journal of Mechanical Sciences, 2007, 49(10): 1139-1155.
15	Nguyen Q H, Hjiaj M, Grognec P L. Analytical approach for free vibration analysis of two-layer Timoshenko beams with interlayer slip[J]. Journal of Sound and Vibration, 2012, 331(12): 2949-2961.
16	Lin J P, Wang G N, Bao G J, et al. Stiffness matrix for the analysis and design of partial-interaction composite beams[J]. Construction and Building Materials, 2017, 156: 761-772.
17	Lin J P, Wang G N, Xu R Q. Variational principles and explicit finite-element formulations for the dynamic analysis of partial-interaction composite beams[J]. Journal of Engineering Mechanics-ASCE, 2020, 146(6): 04020055.
18	Sun Q K, Zhang N, Liu X, et al. An equivalent single-layer theory for free vibration analysis of steel-concrete composite beams[J]. Steel and Composite Structures, 2021, 38(3): 281-291.

相关文章 15

[1]	叶华文,段智超,刘吉林,周渝,韩冰. 正交异性钢⁃混组合桥面的轮载扩散效应[J]. 吉林大学学报(工学版), 2022, 52(8): 1808-1816.
[2]	王立峰,肖子旺,于赛赛. 基于Bayesian网络的多塔斜拉桥挂篮系统风险分析的新方法[J]. 吉林大学学报(工学版), 2022, 52(4): 865-873.
[3]	张彦玲,王灿,张旭,王昂洋,李运生. 不同吊杆形式悬索桥人致振动分析及舒适度评价[J]. 吉林大学学报(工学版), 2022, 52(11): 2644-2652.
[4]	钟昌均,王忠彬,柳晨阳. 悬索桥主索鞍承载力影响因素及结构优化[J]. 吉林大学学报(工学版), 2021, 51(6): 2068-2078.
[5]	陈巍,万田保,王忠彬,厉萱,沈锐利. 悬索桥主缆除湿的内部送气管道设计与性能[J]. 吉林大学学报(工学版), 2021, 51(5): 1749-1755.
[6]	郭殊伦,钟铁毅,闫志刚. 大跨度斜拉桥拉索的抖振响应计算方法[J]. 吉林大学学报(工学版), 2021, 51(5): 1756-1762.
[7]	高凯,刘纲. 全局临界强度分枝-约界法的有效强度改进[J]. 吉林大学学报(工学版), 2021, 51(2): 597-603.
[8]	宫亚峰,宋加祥,谭国金,毕海鹏,刘洋,单承新. 多车桥梁动态称重算法[J]. 吉林大学学报(工学版), 2021, 51(2): 583-596.
[9]	孔庆雯,谭国金,王龙林,王勇,魏志刚,刘寒冰. 基于有限元方法的裂缝箱梁桥自振特性分析[J]. 吉林大学学报(工学版), 2021, 51(1): 225-232.
[10]	陈华,陈耀嘉,谢斌,王鹏凯,邓朗妮. CFRP筋粘结式锚固体系界面失效演化机制及粘结强度计算[J]. 吉林大学学报(工学版), 2020, 50(5): 1698-1708.
[11]	宫亚峰,宋加祥,毕海鹏,谭国金,胡国海,林思远. 装配式箱涵结构缩尺模型静载试验及有限元分析[J]. 吉林大学学报(工学版), 2020, 50(5): 1728-1738.
[12]	高昊,王君杰,刘慧杰,王剑明. 连续梁桥地震行为可控设计准则及实用装置[J]. 吉林大学学报(工学版), 2020, 50(5): 1718-1727.
[13]	蒲黔辉,刘静文,赵刚云,严猛,李晓斌. 高性能树脂混凝土加固混凝土偏压柱承载力理论分析[J]. 吉林大学学报(工学版), 2020, 50(2): 606-612.
[14]	张云龙,郭阳阳,王静,梁东. 钢-混凝土组合梁的固有频率及其振型[J]. 吉林大学学报(工学版), 2020, 50(2): 581-588.
[15]	王伯昕,杨海涛,王清,高欣,陈小旭. 基于补充改进集合经验模态分析法⁃多尺度排列熵分析桥梁振动信号优化滤波方法[J]. 吉林大学学报(工学版), 2020, 50(1): 216-226.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

阶次	SD/RI梁	仅SD梁	E-B梁
1	158.29	158.69 （0.3%）	165.29 （4.4%）
2	542.04	546.49 （0.8%）	618.90 （14.2%）
3	1077.90	1093.73 （1.5%）	1373.02 （27.4%）
4	1709.64	1745.80 （2.1%）	2428.52 （42.0%）
5	2408.85	2474.51 （2.7%）	3785.50 （57.1%）